Курсовая работа: Некоторые приложения определенного интеграла в математике
Курсовая работа студента гр. МТ-21
Нургалиев А.З.
Павлодарский университет
Павлодар 2005 год.
1. Введение.
В курсовой работе рассмотрены вопросы некоторого приложения определенного интеграла. Цель: изучить актуальность применения определенного интеграла и широту его использования в математике, оценить ее практическую и теоретическую значимость.
При разработки данного вопроса, был также рассмотрен несобственный интеграл, как частный случай определенного интеграла, его определение и виды.
2. Определенный интеграл.
Пусть
функция f(x) задана в некотором промежутке [a,b]. Разобьем этот промежуток
произвольным образом на части, вставив между a и b точки деления: ![]() . Наибольшую
из разностей
. Наибольшую
из разностей
![]() (i=0,1,2, …,n-1) будем впредь обозначать через
λ.
(i=0,1,2, …,n-1) будем впредь обозначать через
λ.
Возьмем
в каждом из частных промежутков ![]() по произволу точку
по произволу точку ![]()
![]()
и составим сумму
![]() .
.
Говорят,
что сумма σ при λ→0 имеет (конечный) предел I, если для каждого
числа ε>0 найдется такое число δ>0, что, лишь только
λ<δ (т.е. основной промежуток разбит на части, с длинами ![]() ), неравенство
), неравенство
![]()
выполняется
при любом выборе чисел ![]() .
.
Записывают это так:
![]() . (1)
. (1)
Этому
определению «на языке ε-δ», как обычно, противопоставляется
определение «на языке последовательностей». Представим себе, что промежуток
[α,b] последовательно разбивается на части, сначала одним способом, затем
– вторым, третьим и т.д. Такую последовательность разбиений промежутка на части
мы будем называть основной, если соответствующая последовательность значений ![]() сходится к нулю.
сходится к нулю.
Равенство
(1) можно понимать теперь и в том смысле, что последовательность значений суммы
σ, отвечающая любой основной последовательности разбиений промежутка,
всегда стремится к пределу I, как бы ни выбирать при этом ![]() .
.
Второе определение позволяет перенести основные понятия и предложения теории пределов и на этот новый предел.
Конечный предел I суммы σ при λ→0 называется определенным интегралом функции f(x) в промежутке от α до b и обозначается символом
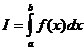 ;
;
в случае существования такого предела функции f(x) называется интегрируемой в промежутке [α,b].
Числа α и b носят название, соответственно, нижнего и верхнего пределов интеграла. При постоянных пределах определенный интеграл представляет собой постоянное число.
3. Несобственные интегралы.
Пусть
f непрерывна на луче на луче ![]() и F(x) – первообразная для f на луче
и F(x) – первообразная для f на луче ![]() . Если
существует
. Если
существует
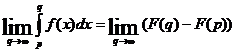 ,
,
то
этот предел обозначается 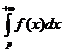 и называется сходящимся несобственным
интегралом.
и называется сходящимся несобственным
интегралом.
Несобственные
интеграл вида 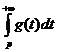 и аналогичный интеграл
и аналогичный интеграл![]() получаются
при замене в интеграле Римана с помощью функции t=t(x), непрерывной и
дифференцируемой на полуинтервале [a,b) ( или (a,b] ) и являющейся бесконечно
большой определенного знака при
получаются
при замене в интеграле Римана с помощью функции t=t(x), непрерывной и
дифференцируемой на полуинтервале [a,b) ( или (a,b] ) и являющейся бесконечно
большой определенного знака при ![]() (или
(или ![]() ).
).
Здесь
существенно, что особой точкой функции t является именно конец (левый или
правый) отрезка [a,b]. Если особой точкой t(x) (как в разобранном выше примере)
является внутренняя точка с интервала (a,b), то 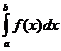 разбивается на
разбивается на 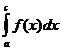 и
и 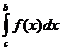 , и переход к
аргументу t делается раздельно в каждом из слагаемых.
, и переход к
аргументу t делается раздельно в каждом из слагаемых.
Пример.
Вычислим
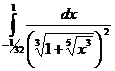 .
.
Пусть
![]() ,
,
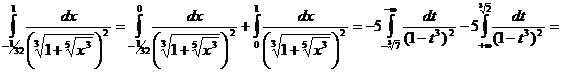
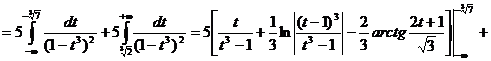
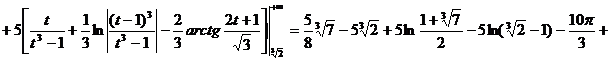
![]()
Другим
видом несобственного интеграла является интеграл 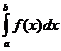 , если функция
f не ограничена на
, если функция
f не ограничена на ![]() , но
непрерывна на
, но
непрерывна на ![]() при любом
при любом ![]() ,
, ![]() (или на
(или на ![]() ), т.е. не
ограничена в окрестности точки
), т.е. не
ограничена в окрестности точки ![]() (точки b).
(точки b).
Этот интеграл существует (сходится), если существует:
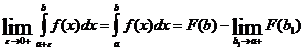
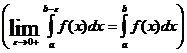
Пример.
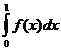 , если
, если 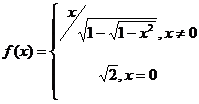
f(x)
непрерывна на [0,1]. После замены ![]() получаем
получаем
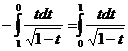 .
.
![]() не ограничена на [0,1], т.к. первообразная
функция
не ограничена на [0,1], т.к. первообразная
функция ![]() на
на ![]() при любом
при любом ![]() ,
, ![]() равна:
равна: ![]() , то
, то
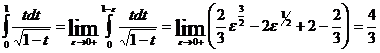 .
.
Несобственный интеграл может появится и при интегрировании по частям.
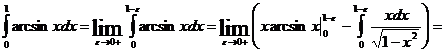
![]() ,
,
т.е.
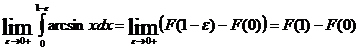 ,
,
где
![]() - первообразная для arcsinx на [0,1].
- первообразная для arcsinx на [0,1].
4.1.Формула Валлиса.
Для вывода формулы Валлиса необходимо вычислить следующий интеграл:
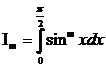 (при натуральном m).
(при натуральном m).
Интегрируя по частям, найдём
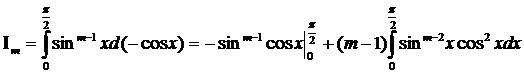 .
.
Двойная
подстановка обращает в нуль. Заменяя ![]() через
через ![]() , получим
, получим
![]()
откуда рекуррентная формула:
![]() ,
,
по
которой интеграл ![]() последовательно приводится к
последовательно приводится к ![]() и
и ![]() . Именно, при
m=2n имеем
. Именно, при
m=2n имеем
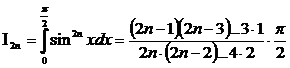 ,
,
если же m=2n+1, то
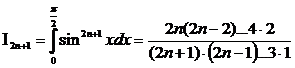 .
.
Такие
же точно результаты получаются и для ![]() .
.
Для более короткой записи найденных выражений воспользуемся символом m!!(произведение натуральных чисел, не превосходящих m и одной с ним чётности). Тогда можно будет написать
 |
|
|
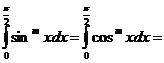 (1)
(1)
Из формулы (1) можно вывести знаменитую формулу Валлиса (J. Wallis).
Предполагая
0<x<![]() , имеем
неравенства
, имеем
неравенства
![]() .
.
Проинтегрируем
эти неравенства в промежутке от 0 до ![]() :
:
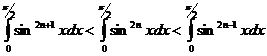
Отсюда, в силу (1), находим
![]()
или
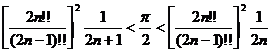 .
.
Так как разность между двумя крайними выражениями
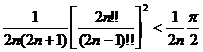 ,
,
очевидно,
стремится к 0 при ![]() , то
, то ![]() является их общим пределом. Итак,
является их общим пределом. Итак,
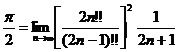
или
![]() .
.
Отсюда в свою очередь вытекает
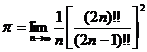
Эта
формула носит название формулы Валлиса. Она дает довольно простое выражение
числа p
через натуральные числа. Теоретически этот результат интересен. Что касается
ценности этой формулы как средства фактического вычисления p,
то она невелика. Именно, чтобы получить удовлетворительную точность, надо взять
n довольно большим, а тогда выражение ![]() оказывается весьма громоздким.
оказывается весьма громоздким.
4.2. Применение формулы Валлиса для интеграла Эйлера-Пуассона.
Интеграл Эйлера-Пуассона имеет вид:
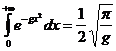 ;
;
Приведём метод его нахождения. Мы знаем что положив:
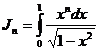 (т.к.
(т.к. 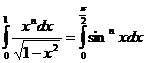 ),
),
имеем соотношение:
![]() ;
;
отсюда заключаем:
![]() ,
,
![]()
что дает:
![]() .
.
Установив
это, замечаем, что предел отношения ![]() при бесконечно большом n равен единице;
действительно, так как
при бесконечно большом n равен единице;
действительно, так как ![]() убывает при возрастании n, то мы имеем
неравенство:
убывает при возрастании n, то мы имеем
неравенство:
![]()
или:
![]() .
.
Мы
видим, следовательно, что ![]() заключается между единицей и дробью
заключается между единицей и дробью ![]() , которая
также равна единице при бесконечном n.
, которая
также равна единице при бесконечном n.
Установив это, получаем равенство:
![]() ,
,
которое нам дает, если заставим n бесконечно возрастать:
![]() ,
,
и, следовательно:
![]() .
.
Полагая
теперь ![]() в интеграле
в интеграле ![]() , мы получим
следующее новое выражение:
, мы получим
следующее новое выражение:
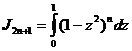 ;
;
заменив
затем z на ![]() , получаем:
, получаем:
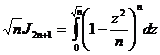
и, следовательно, при бесконечном n
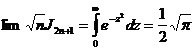 .
.
Достаточно
затем положить ![]() , чтобы
установить результат, к которому мы стремились:
, чтобы
установить результат, к которому мы стремились:
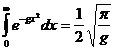 .
.
4.3. Вывод формулы Тейлора с остаточным членом в интегральной форме.
Формула
интегрирования по частям: 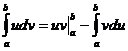 ,
,
а обобщенная формула примет вид:
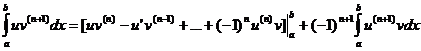 . (1)
. (1)
Положим,
что в формуле (1)![]() . Тогда
. Тогда ![]() ,
, ![]() , …,
, …, ![]() ,
, ![]() ; при x=b все
функции v, v’, …,
; при x=b все
функции v, v’, …, ![]() обращаются в нуль. Пользуясь для u, u’, u’’, …
функциональным обозначением f(x), f’(x), f’’(x), …, перепишем (1) в виде
обращаются в нуль. Пользуясь для u, u’, u’’, …
функциональным обозначением f(x), f’(x), f’’(x), …, перепишем (1) в виде
![]()
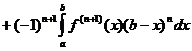 .
.
Отсюда получается формула Тейлора с дополнительным членом в виде определенного интеграла
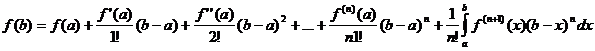 .
.
Заменим
здесь b через x, а ![]() через
через ![]() :
:
![]()
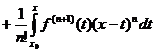 .
.
Новое выражение для дополнительного члена, не содержит никаких неизвестных чисел.
Если
угодно, из этого выражения можно было бы вывести и уже знакомые нам формы
дополнительного члена. Например, воспользовавшись тем, что множитель ![]() подинтегральной функции не меняет знака, можно
применить к последнему интегралу обобщенную теорему о среднем
подинтегральной функции не меняет знака, можно
применить к последнему интегралу обобщенную теорему о среднем
 ,
,
где
с содержится в промежутке ![]() . Таким образом,
мы вновь получили лангранжеву форму дополнительного члена.
. Таким образом,
мы вновь получили лангранжеву форму дополнительного члена.
5. Заключение.
В курсовой работе даны определения определенного и несобственного интеграла и его виды, рассмотрены вопросы некоторого приложения определенного интеграла. В частности, формула Валлиса, имеющая историческое значение, как первое представление числа p в виде предела легко вычисляемой рациональной варианты, а также вычисление интеграла Эйлера-Пуассона с помощью этой формулы. Рассмотрен способ получения формулы Тейлора с дополнительным членом в интегральной форме.
Формулой Валлиса в теоретических исследованиях пользуются и сейчас (например, при выведении формулы Стирлинга). Что касается фактического приближенного вычисления p, то существуют методы, гораздо более быстро ведущие к цели.
Интеграл Эйлера-Пуассона применяется при вычислении более сложных несобственных интегралов, встречается в теории вероятности.
Новое выражение для дополнительного члена в формуле Тейлора интересно тем, что оно не содержит никаких неизвестных чисел.
Данную курсовую работу можно использовать в качестве лекционного и справочного материала.
Список литературы
Фихтенгольц Г. М. «Курс дифференциального и интегрального исчисления»(II том) – Москва, 1970г.
Пискунов Н.С. «Дифференциальное и интегральное исчисления»(I том) - Москва, 1970г.
Эрмит Ш. «Курс анализа» - Москва, 1936г.
| Шпоры по математическому анализу | |
|
Производные и дифференциалы высших порядков Опр-ие: производной n-го порядка (n 2) функции у=f(х) называется производная (первого порядка) от ... Определение определенного интеграла по конечному промежутку [a,b] неприменимо к случаю бесконечного промежутка, например [a, +=). Дело в том, что нельзя промежуток [a ... о это предел называют несобственным интегралом от функции f(x) на промежутке от а до += и обозначают |
Раздел: Рефераты по математике Тип: реферат |
| Курс лекций по теории вероятностей | |
|
Раздел 1. Классическая вероятностная схема 1.1 Основные формулы комбинаторики В данном разделе мы займемся подсчетом числа "шансов". О числе шансов ... 1. Точка с координатами ѭ, ѭ бросается наудачу в квадрат со стороной 1. Доказать, что для любых х, у R события A = { ѭ <x} и B= { ѭ <y} независимы. Если функция F: R [0, 1] удовлетворяет свойствам (F1)-(F3), то F есть функция распределения некоторой случайной величины ѭ, то есть найдется вероятностное пространство (Ѭ, Ѭ, Р) и ... |
Раздел: Рефераты по математике Тип: реферат |
| Шпаргалки по геометрии, алгебре, педагогике, методике математики (ИГПИ ... | |
|
Кольцом называется числ. множ. На котором выполняются три опер-ии: слож, умнож, вычит. Полем наз. Числ множ. На котором выполняются 4 операции: слож ... 1. Ґf(x)ЄP[x], f(x)|f(x). 2. f(x), g(x)ЄP[x], g(x)|f(x) и f(x)|g(x) => f(x) и g(x) ассоц-ы, f(x)=cg(x), cЄP[x]. 3. g(x)|f(x) и ѭ(x)|g(x) => g(x)|(f(x)=ѭ(x)). 4. Если f1(x), f2(x ... x)-(f(x),ѭ1(x) + g(x)ѭ1(x)) q1(x) = g(x)-f(x)ѭ1(x)q1(x)-g(x)ѭ1(x)q1(x) = f(x)(-ѭ1(x)q1(x)) + g(x)(1-ѭ1(x)q1(x)) = f(x)ѭ2(x)+g(x)ѭ2(x). r2(x) = f(x)ѭ2(x)+g(x)ѭ2(x). Подставим ... |
Раздел: Рефераты по математике Тип: реферат |
| Свойства бесконечной величины. Различие актуальной и потенциальной ... | |
|
Содержание Введение Зенон о бесконечной величине Аристотель о потенциальной и актуальной бесконечности Николай Кузанский о бесконечном Больцано ... Ахиллес настигнет черепаху, если в бесконечно малый промежуток времени он пройдет не бесконечно малое расстояние. Математическое потенциально бесконечное Кантор называет "несобственно-бесконечным". |
Раздел: Рефераты по философии Тип: курсовая работа |
| Производная и ее применение в алгебре, геометрии, физике | |
|
Гимназия №1 города Полярные Зори Алгебра, геометрия, физика. Научная работа ТЕМА "ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ В АЛГЕБРЕ, ГЕОМЕТРИИ, ФИЗИКЕ ... Говорят также, что в промежутке а<х<b линия y = f(x) лежит выше (ниже) линии у=ѭ(х), если в этом промежутке каждая точка первой линии лежит выше (ниже) соответствующей ей точки ... Действительно, отношение =y/=x отличается от своего предела f '(x) на бесконечно малую ѭ, причем ѭ = 0 при стремлении =x к нулю, |
Раздел: Рефераты по математике Тип: реферат |
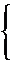 четном нечётном.
четном нечётном.