Статья: Геометрические свойства регулярного круглого конуса в пространстве
Раздел: Рефераты по математике
Тип: статья
Асп. Коробова К. В.
Кафедра математического анализа.
Северо-Осетинский государственный университет
Приведены
явные формулы для вычисления множеств положительных и отрицательных частей
произвольного элемента в пространстве ![]() ,
упорядоченном круглым регулярным конусом. Определено множество элементов, на
котором реализуется минимум в формуле расстояния от элемента до конуса, и
исследуется вопрос о совпадении этого множества с множеством положительных
частей элемента.
,
упорядоченном круглым регулярным конусом. Определено множество элементов, на
котором реализуется минимум в формуле расстояния от элемента до конуса, и
исследуется вопрос о совпадении этого множества с множеством положительных
частей элемента.
Введение
Теория
конусов является актуальным разделом функционального анализа и находит большое
применение во многих областях математики. Геометрическим свойствам пространств,
упорядоченных конусами различного вида, посвящены работы Л. В. Канторовича, Б.
3. Вулиха [1,2], М. А. Красносельского [3], В. Т. Худалова [4,5]. В работе
автора [6] дано общее описание регулярного круглого конуса в пространстве ![]() и описаны некоторые его свойства. Данная
статья посвящена дальнейшему исследованию порядковых свойств пространства
и описаны некоторые его свойства. Данная
статья посвящена дальнейшему исследованию порядковых свойств пространства ![]() .
.
1. Предварительные сведения
Приведем необходимые для дальнейшего использования определения и результаты.
1.1. Пусть Е – банахово пространство над полем действительных чисел R, Е+ – конус в Е. Конус Е+ называется регулярным, если выполнены следующие условия:
±х ≤ у Þ ||х|| ≤ ||y|| для любых х, у Î Е,
для любого х Î Е и любого e > 0 существует у Î Е+ такой, что ±х ≤ у и ||у|| ≤ (1+e) ||х||.
Регулярный конус Е+ называется строго регулярным, если выполнено условие (2) при e = 0, т. е.
(2') для любого х Î Е существует у Î Е+ такой, что ±х ≤ у и ||y|| = ||х||.
Упорядоченное замкнутым строго регулярным конусом Е+ пространство Е обозначают (Е, Е+) Î (Â), см. [1,2].
1.2. Одним из наиболее общих методов построения конуса в произвольном банаховом пространстве, обладающего свойствами нормальности, несплющенности, а также другими свойствами, является следующий: пусть X – банахово пространство, f Î X* – произвольный непрерывный линейный функционал на X такой, что ||f|| = 1. Для любого aÎ (0,1] определим K(f,α):={xÎX: f(x) ≥ a||х||}.
Если Н – гильбертово пространство над R, то для любого aÎН, ||a|| = 1, конус К(а, a) имеет вид:
K(a, α) = {x Î X : (a, x) ≥ a ||x||}.
Если
dim H > 1, то для любого а Î Н, ||a|| = 1, конус К (а, a) строго регулярен в Н
тогда и только тогда, когда a = ![]() [5].
[5].
1.3.
Отметим, что класс регулярных конусов в пространствах ![]() и l1 совпадает с классом строго регулярных
конусов [5]. Данная работа опирается на следующее описание всех регулярных
круглых конусов, полученных в [4].
и l1 совпадает с классом строго регулярных
конусов [5]. Данная работа опирается на следующее описание всех регулярных
круглых конусов, полученных в [4].
Теорема.
Конус K(f, a)
является регулярным ![]() , n > l1
только при двух значениях a Î (0,1]:
, n > l1
только при двух значениях a Î (0,1]:
при
a
= 1 каждая координата вектора f = (f1, f2,..., fn) равна +1 или – 1; при этом
имеется 2n конусов, порождающих упорядоченные банаховы пространства, порядково
изоморфные и линейно изометричные пространству ![]() с естественным конусом положительных
элементов;
с естественным конусом положительных
элементов;
при
a
= 0,5 одна из координат (j-я координата) вектора f = (f1, f2,..., fn) равна ±1, а
все остальные – нули; при этом имеется 2n конусов, порождающих упорядоченные
банаховы пространства, порядково изоморфные и линейно изометричные пространству
![]() с конусом
с конусом
Kj
= {х = (x1,x2,...,xn) : xj ≥ 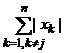 }. (1)
}. (1)
1.4. Пусть (Е, Е+) Î (Â). Для любого х Î Е обозначим через |Х| множество элементов у Î Е таких, что ± x ≤ у и ||x|| = ||y||. Любой элемент этого множества называется метрическим модулем элемента x.
Положим
X+ = ½ x + ½|X|, X− = −½ x + ½|X| .
Множества Х+ и Х− называются множествами положительных (соответственно отрицательных) частей элемента x. Если у Î |Х|, т.е. ±x ≤ у и ||у|| = ||x||, то положим x+ = (у + x)/2, x− = (у – x)/2, |x| = x+ + x−. Из определения следует, что |x| ≥ ± x, причем
x = x+ − x−, |x| = x+ + x−, ||x+ - x−|| = ||x+ + x−||, ||x|| = |||x|||.
1.5. Конус Е+ в упорядоченном банаховом пространстве (Е, Е+) Î (Â) называется достижимым, если для любого x Î Е существует элемент Рх Î Е+, на котором реализуется минимум в формуле расстояния от х до Е+, т. е.
d(x, E+) = inf{||а – x|| : a Î E+} = ||Рx – x||.
Множество всех таких Рх обозначается М(х).
1.6. При вычислении расстояния от точки до конуса воспользуемся следующим результатом из [5].
Пусть (Е, Е+) Î (Â) и х Î Е+. Элемент x+ Î Е+ является ближайшим к х элементом конуса Е+ тогда и только тогда, когда существует f Î Е*+, ||f|| = 1, такой, что f(x+) = 0, f(x-) = ||x-||. В этом случае d(x, Е+) = ||x-||.
1.7.
Пусть E – банахово пространство над R со строго регулярным замкнутым конусом
Е+. Элементы x, у Î
Е+ называются н-дизъюнктными или ортогональными по Роберу (обозначается x ![]() у), если ||x +
λу|| = ||x – λу|| для любого λ ≥ 0.
у), если ||x +
λу|| = ||x – λу|| для любого λ ≥ 0.
2. Описание множеств |Х|, Х+, Х-
Рассмотрим
пространство ![]() ,
упорядоченное регулярным круглым конусом K(f,a), где a =
0,5 и функционал f имеет первую координату, равную единице, а остальные
координаты нулевые:
,
упорядоченное регулярным круглым конусом K(f,a), где a =
0,5 и функционал f имеет первую координату, равную единице, а остальные
координаты нулевые:
K1 = {x = (x1, x2, ..., xn) : x1 ≥ |x2| + … + |xn|}.
Все
результаты легко перенести на общий случай (1) с помощью изометричного
преобразования. В дальнейшем, если не указано иное, будем обозначать через X = ![]() .
.
Опишем
множества |Х|, Х+, Х-
для произвольного элемента x = (x1, ..., xn) Î ![]() . Заметим, что
частный случай разложения элемента х на ортогональные по Роберу положительную и
отрицательную части рассмотрен в [6].
. Заметим, что
частный случай разложения элемента х на ортогональные по Роберу положительную и
отрицательную части рассмотрен в [6].
2.1.
Пусть x1 = 0. Найдем элемент конуса, который мажорирует элементы ± х и равен им
по норме, т. е. у = (у1, …, yn) : y1 ≥ ![]() , y ≥ ±
х, ||y|| = ||x||. Такой элемент описывает следующая система:
, y ≥ ±
х, ||y|| = ||x||. Такой элемент описывает следующая система:
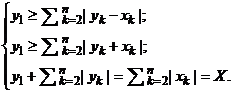
Сложив
первые два неравенства, получим оценку у1 ≥ X. С другой стороны, из
третьего равенства видно, что у1 ≤ X. Тогда у1 = X, ![]() = 0,
следовательно yk = 0 для любого
= 0,
следовательно yk = 0 для любого ![]() . Получаем
следующее представление метрического модуля элемента х и его положительной и
отрицательной части
. Получаем
следующее представление метрического модуля элемента х и его положительной и
отрицательной части
![]() ,
,
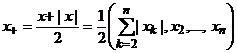 ,
,
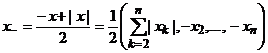 .
.
2.2. Пусть x1 > 0. В этом случае система, описывающая элемент у Î |Х|, имеет вид:
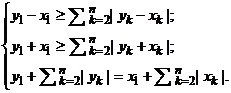
Аналогичные
действия позволяют утверждать, что X≤у1≤X + х1, т.е. у1 представим
в виде у1 = X + λх1, где 0 ≤ λ ≤ 1. Последовательно
подставляя значение у1 в систему, имеем: ![]() -|yk – xk|) ≥
≥ х1(l – λ) =
-|yk – xk|) ≥
≥ х1(l – λ) = ![]() , с другой
стороны, |уk| = |xk + (yk – xk)| ≥ ≥ |xk| – |yk – xk|. В итоге
получаем:
, с другой
стороны, |уk| = |xk + (yk – xk)| ≥ ≥ |xk| – |yk – xk|. В итоге
получаем:
|xk|
= |yk| + |yk − xk| (![]() ).
).
Из этого равенства следует, что уk и хk – yk – одного знака, что приводит к следующим выводам:
если (xk − yk) > 0 и yk > 0, то 0 < yk < xk ;
если (xk − yk) < 0 и yk < 0, то xk < yk < 0;
если (хк – yk) = 0 и yk = 0, то хk = уk = 0.
Из
чего следует, что каждая координата уk (![]() ) представима
в виде уk = λkхk, 0 ≤ λk ≤ 1.
) представима
в виде уk = λkхk, 0 ≤ λk ≤ 1.
Отметим равенство, используемое в дальнейшем:
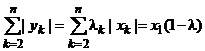 .
.
Итак, при x1 > 0 имеем:
![]()
где
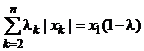 , 0 ≤
λ, λk ≤ 1};
, 0 ≤
λ, λk ≤ 1};
![]()
где
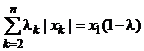 , 0 ≤
λ, λk ≤ 1};
, 0 ≤
λ, λk ≤ 1};
![]()
где
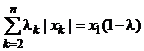 , 0 ≤
λ, λk ≤ 1}.
, 0 ≤
λ, λk ≤ 1}.
2.3. Пусть x1 < 0. Система, описывающая элемент у Î |Х|, на этот раз имеет вид:
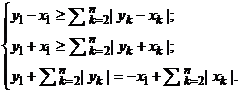
Выполнив аналогичные пункту 2.2 действия, получим X ≤ у1 ≤ X – х1. В этом случае y1 = Х + λ|x1|, где 0 ≤ λ ≤ 1. Подставляя последовательно значение у1 в систему, получаем
![]()
![]() и
и ![]() .
.
Откуда выводим:
|xk|
= |yk| + |yk + xk| (![]() ).
).
Отсюда
следует, что – yk и (xk + yk) – одного знака. Вновь получаем, что уk =
–λkxk , 0≤λk≤1. При этом ![]() =
=![]() =
= ![]() .
.
Итак, при х1 < 0 имеем:
![]()
где
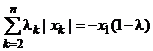 , 0 ≤
λ, λk ≤ 1};
, 0 ≤
λ, λk ≤ 1};
![]()
где
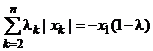 , 0 ≤
λ, λk ≤ 1};
, 0 ≤
λ, λk ≤ 1};
![]()
где
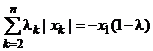 , 0 ≤
λ, λk ≤ 1}.
, 0 ≤
λ, λk ≤ 1}.
2.4. Общий случай. Для произвольного элемента х = (x1, ..., xn) и круглого регулярного конуса Kj (1) имеем:
![]()
где
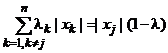 , 0 ≤
λ, λk ≤ 1};
, 0 ≤
λ, λk ≤ 1};
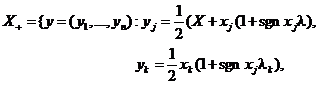
где
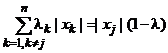 , 0 ≤
λ, λk ≤ 1};
, 0 ≤
λ, λk ≤ 1};
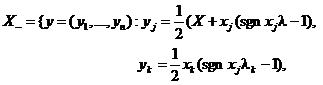
где
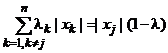 , 0 ≤
λ, λk ≤ 1};
, 0 ≤
λ, λk ≤ 1};
| 2 Труды молодых ученых, 2005 (1) |
3. Нахождение расстояния от элемента до конуса
Пусть элемент x принадлежит конусу К1, т.е. х1 ≥ X. В этом случае d(x, K1) = 0, а ближайшим элементом конуса является он сам.
Пусть элемент х принадлежит конусу – К1, т.е. -х1 ≥ X. В этом случае очевидно d(x, K1) = ||х||, а ближайшим элементом конуса является ноль.
Пусть х1 = 0 и элемент х не принадлежит конусу ±К1. Покажем, что d(x, K1) = ||х–||, а ближайшим элементом конуса является х+. Согласно следствию 2.2.13 [5], для этого необходимо найти функционал f Î К*1 такой, что ||f|| = 1, f(x+) = 0, f(x-) = ||x-||,
где x+ – x- = x, ||x+ + x-|| = ||x||.
В
качестве такого функционала выберем f=(1, –sgn x2, ...,–sgn xn). Для любого
элемента конуса аÎК1
справедливо f(а)=a1 –![]() , т. е. f положительный
функционал. Очевидно, что его норма равна единице. Элементы x+ и x–,
вычисляемые по формулам 2.1, удовлетворяют условиям следствия 2.2.14 [5]. Кроме
того,
, т. е. f положительный
функционал. Очевидно, что его норма равна единице. Элементы x+ и x–,
вычисляемые по формулам 2.1, удовлетворяют условиям следствия 2.2.14 [5]. Кроме
того,
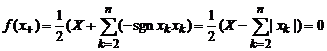 ,
,
![]() .
.
Учитывая,
что ||x–|| = ![]() || (Х, x2, ...
, хn)|| = X, имеем, что f(x-) = =||x-||. Таким образом, условия следствия 2.2.14 [5]
выполняются полностью, и мы приходим к выводу, что
|| (Х, x2, ...
, хn)|| = X, имеем, что f(x-) = =||x-||. Таким образом, условия следствия 2.2.14 [5]
выполняются полностью, и мы приходим к выводу, что
d(x,
K1) = || x-||
= ![]() =X, а x+
является ближайшим к х элементом конуса.
=X, а x+
является ближайшим к х элементом конуса.
3.4. Пусть X > х1 > 0. Положив λ = 0 в формулах 2.2, получим:
![]()
![]() ) .
) .
В этом случае очевидно, что x+ – x- = x, || x+ + x-|| = ||x||.
Рассматривая функционал из 3.3, находим:
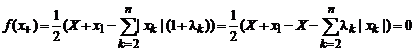 ,
,
![]() .
.
Заметим,
что в этих рассуждениях использован результат, полученный в 2.2, о том, что ![]() .
.
В
итоге получаем, что d(x, K1) = ||x-|| = ![]() , a x+
является ближайшим к x элементом конуса.
, a x+
является ближайшим к x элементом конуса.
3.5. Пусть х1 < 0 и – х1 > X. Если λ = 0 в формулах 2.3, то элементы
![]()
![]() )
)
удовлетворяют условиям x+ – x- = x и ||x+ + x-|| = ||x||, причем f(x+) = 0, f(x-) = ||x-||, где f – функционал из 3.3.
Таким
образом, в этом случае d(x, K1) = ||x-|| = ![]() , a x+ –
ближайший к x элемент конуса.
, a x+ –
ближайший к x элемент конуса.
Аналогичные рассуждения показывают, что данные результаты справедливы и для конуса Kj.
3.6. Данные рассуждения подтверждают результат утверждения 2.3 из [6] о том, что
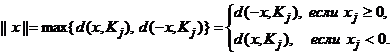
4. Описание множества М(х)
Элемент x принадлежит конусу К1. В этом случае расстояние d(x, K1) = ||x–|| = 0. Если а = (a1, ..., аn) Î М(x), то а Î К1 и ||а – x|| = 0, откуда следует, что а = x и M(x) = {x}.
Элемент х принадлежит конусу –К1. В этом случае x1 ≤ –X и расстояние
d(x,
К1) = ||x||. Если a = (a1, ..., аn) Î М(x), то a1 ![]() = A и ||a –
x|| = ||x||, что равносильно |а1 – x1| +
= A и ||a –
x|| = ||x||, что равносильно |а1 – x1| + ![]() = –x1 + +
= –x1 + +![]() . Откуда
следует, что а1 =
. Откуда
следует, что а1 =![]() -
- ![]() ≥
≥ ![]() =A.
=A.
Получаем,
что ![]() ≥
≥ ![]()
![]() ≥ ≥
≥ ≥ ![]() .
.
Равенство
| xk – аk| + |аk| = |xk| для любого ![]() означает, что аk и (xk – аk) – одного знака,
т. е. аk = ak
xk, где 0 ≤ ak
≤ 1 для любого
означает, что аk и (xk – аk) – одного знака,
т. е. аk = ak
xk, где 0 ≤ ak
≤ 1 для любого ![]() . Выражение
для а1 имеет вид: а1 =
. Выражение
для а1 имеет вид: а1 = ![]() .
.
В итоге получаем, что
![]() где 0≤ak≤1,
где 0≤ak≤1,![]() }.
}.
4.3.
x1 = 0 и элемент х не принадлежит конусу К1. Пусть а = (a1, ..., an) Î
М(x). Из определения М(х) следует, что a1 ≥ А и ||а – x|| = =![]() + |a1| =
+ |a1| = ![]() . Из последних
равенств получаем: а1 =
. Из последних
равенств получаем: а1 = ![]() –
– ![]() ≥
≥ ![]() или следующую цепочку
или следующую цепочку ![]() ≥
≥ ![]() =
= ![]() + +
+ +![]() ≥
≥ ![]() . Это равносильно
. Это равносильно
![]() + +
+ +![]() =
= ![]() . В итоге
вновь получаем равенство
. В итоге
вновь получаем равенство
|xk
−ak| + |ak| = |xk| (![]() ),
),
которое равносильно утверждению, что
![]() где 0≤ak≤1,
где 0≤ak≤1, ![]() }.
}.
4.4.
Пусть x1 > 0 и элемент x не принадлежит конусу K1. Если а = (a1, ..., аn) Î
М(x), то ||a – x|| = ||x–|| = d(x, К1) = ![]() – x1
– x1
или
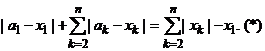
Так
как a Î
K1 , то а1 ≥ ![]() . Тогда
последовательно получаем a1 ≤ |а1 – x1| + x1 =
. Тогда
последовательно получаем a1 ≤ |а1 – x1| + x1 = ![]() -
- ![]() ≤
≤ ![]() ≤ a1 , что равносильно системе
≤ a1 , что равносильно системе
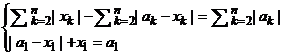
или
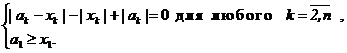
Получаем,
что (аk – xk) и xk – одного знака, т. е. аk = akxk, где 0 ≤ ak ≤
1 для любого ![]() . Подставив в
(*), имеем а1 +
. Подставив в
(*), имеем а1 + ![]() =
= ![]() .
.
Таким
образом, выражение для а1 имеет вид: а1 =![]() .
.
В итоге получаем, что если х1 > 0, то
![]() где 0≤ak≤ 1,
где 0≤ak≤ 1, ![]() }.
}.
4.5.
Пусть x1 < 0 и элемент х не принадлежит конусу –К1, т.е. –x1 < ![]() .
.
Если
а = (a1, ..., аn) Î
М(x), то ||a-x|| = ||x–|| = d(x, К1) =![]() –x1
–x1
или
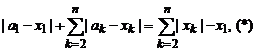
или
![]()
Откуда
a1= ![]() -
- ![]() ≥
≥![]() . В то же
время
. В то же
время ![]() ≥
≥ ![]() +
+ ![]() ≥
≥ ![]() . Из
последнего неравенства получаем, что (ak – xk) и (xk) – одного знака для любого
k, т. е. аk = ak
xk, где 0 ≤ ak
≤ 1 для любого
. Из
последнего неравенства получаем, что (ak – xk) и (xk) – одного знака для любого
k, т. е. аk = ak
xk, где 0 ≤ ak
≤ 1 для любого ![]() . Тогда a1=
. Тогда a1=![]() –
–![]() =
=![]() . Получаем,
что (4.4) верно и для этого случая.
. Получаем,
что (4.4) верно и для этого случая.
5. Описание множества M(x)∩K1
Интересен вопрос о взаимоотношении множества положительных частей элемента и множества элементов, на которых достигается расстояние от элемента до конуса.
Пусть
элемент x принадлежит конусу К1. В этом случае М(х) = {x}, а Х+ = {![]() (Х + x1(1 +
λ), x2(1 + λ2), ..., xn(1 + λn)), 0 ≤ λ, λk ≤
1,
(Х + x1(1 +
λ), x2(1 + λ2), ..., xn(1 + λn)), 0 ≤ λ, λk ≤
1, ![]() = x1(1 – λ)}. При λk = 1 получим
λ = 0 и Х+ = {x}, т.е. М(х) ∩ Х+ = {x} и М(х) Ì
Х+.
= x1(1 – λ)}. При λk = 1 получим
λ = 0 и Х+ = {x}, т.е. М(х) ∩ Х+ = {x} и М(х) Ì
Х+.
Пусть элемент x принадлежит конусу –К1. Если аÎ М(x)∩Х+, то, учитывая формулы 4.2 и 2.2, получим:
![]() (
(![]() + x1(1 –
λ), x2(1 – λ2), ... , xn(1 – λn)).
+ x1(1 –
λ), x2(1 – λ2), ... , xn(1 – λn)).
Из
этого равенства следует, что ![]() ) при λk Î[0,1].
Итак, для любого λk,
) при λk Î[0,1].
Итак, для любого λk, ![]() найдется
найдется ![]() такое, что из того, что а Î
Х+ следует, что а Î
М(х). Обратное не всегда верно. В итоге получаем включение М(x) ∩ Х+ = X+
.
такое, что из того, что а Î
Х+ следует, что а Î
М(х). Обратное не всегда верно. В итоге получаем включение М(x) ∩ Х+ = X+
.
5.3. Пусть x1 = 0 и элемент x не принадлежит конусу. Воспользовавшись формулами 4.3 и 2.1, получим М(х) ∩ Х+ = Х+.
5.4. Пусть x1 > 0 и элемент x не принадлежит конусу. Если элемент принадлежит М(х) ∩ Х+ , то выполняется равенство:
![]() (
(![]() + x1(1 +
λ), x2(1 + λ2), ..., xn(1 + λn)),
+ x1(1 +
λ), x2(1 + λ2), ..., xn(1 + λn)),
что равносильно системе
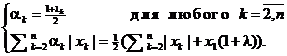
Данные
равенства выполняются, если λk такие, что λ = 0. В этом случае ![]() , т.е.
, т.е.
М(x)∩Х+=![]() .
.
5.5. Пусть x1 < 0 и элемент х не принадлежит конусу –К1. Если элемент принадлежит М(х) ∩ Х+ ,то выполняется равенство:
![]() (
(![]() + x1(1 -
λ), x2(1 - λ2), ..., xn(1 - λn)),
+ x1(1 -
λ), x2(1 - λ2), ..., xn(1 - λn)),
что равносильно системе
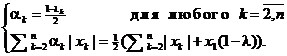
Данные
равенства выполняются, если ![]() ], т. е. М(x) ∩
Х+ = М(х).
], т. е. М(x) ∩
Х+ = М(х).
Список литературы
Вулих Б. 3. Введение в теорию конусов в нормированных пространствах. Калинин.: Изд-во КГУ, 1977.
Вулих Б. 3. Специальные вопросы геометрии конусов в нормированных пространствах. Калинин.: Изд-во КГУ, 1978.
Красносельский М. А. Положительные решения операторных уравнений. М.: Физматгиз. 1962.
Вишняков
Ю. Г., Худалов В. Т. Описание всех регулярных круглых конусов в ![]() . Вестник СОГУ.
Естественные науки. 1999. № 1.
. Вестник СОГУ.
Естественные науки. 1999. № 1.
Худалов В. Т. Упорядоченные банаховы пространства и их приложения. Владикавказ: Иристон, 1999.
Коробова
К. В. О геометрии регулярных круглых конусов в пространствах ![]() и
l1.–Владикавказский мат. журн. 2003. Т. 5, № 3.
и
l1.–Владикавказский мат. журн. 2003. Т. 5, № 3.