Реферат: Nonlinear multi-wave coupling and resonance in elastic structures

Nonlinear multi-wave coupling and resonance in elastic structures

Kovriguine DA

Solutions to the evolution equations describing the phase and amplitude modulation of nonlinear waves are physically interpreted basing on the law of energy conservation. An algorithm reducing the governing nonlinear partial differential equations to their normal form is considered. The occurrence of resonance at the expense of nonlinear multi-wave coupling is discussed.

Introduction

The principles of nonlinear multi-mode coupling were first recognized almost two century ago for various mechanical systems due to experimental and theoretical works of Faraday (1831), Melde (1859) and Lord Rayleigh (1883, 1887). Before First World War similar ideas developed in radio-telephone devices. After Second World War many novel technical applications appeared, including high-frequency electronic devices, nonlinear optics, acoustics, oceanology and plasma physics, etc. For instance, see [1] and also references therein. A nice historical sketch to this topic can be found in the review [2]. In this paper we try to trace relationships between the resonance and the dynamical stability of elastic structures.

Evolution equations

Consider a natural quasi-linear mechanical system with distributed parameters. Let motion be described by the following partial differential equations

(0) ,

where denotes the complex -dimensional vector of a solution;  and  are the  linear differential operator matrices characterizing the inertia and the stuffiness, respectively;  is the -dimensional vector of a weak nonlinearity, since a parameter  is small[1];  stands for the spatial differential operator. Any time  the sought variables of this system  are referred to the spatial Lagrangian coordinates .

Assume that the motion is defined by the Lagrangian . Suppose that at  the degenerated Lagrangian  produces the linearized equations of motion. So, any linear field solution is represented as a superposition of normal harmonics:

.

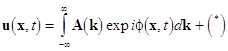Here  denotes a complex vector of wave amplitudes[2];  are the fast rotating wave phases;  stands for the complex conjugate of the preceding terms. The natural frequencies  and the corresponding wave vectors  are coupled by the dispersion relation . At small values of , a solution to the nonlinear equations would be formally defined as above, unless spatial and temporal variations of wave amplitudes . Physically, the spectral description in terms of new coordinates , instead of the field variables , is emphasized by the appearance of new spatio-temporal scales associated both with fast motions and slowly evolving dynamical processes.

This paper deals with the evolution dynamical processes in nonlinear mechanical Lagrangian systems. To understand clearly the nature of the governing evolution equations, we introduce the Hamiltonian function , where . Analogously, the degenerated Hamiltonian  yields the linearized equations. The amplitudes of the linear field solution  (interpreted as integration constants at ) should thus satisfy the following relation , where  stands for the Lie-Poisson brackets with appropriate definition of the functional derivatives. In turn, at , the complex amplitudes are slowly varying functions such that . This means that

(1)  and ,

where the difference  can be interpreted as the free energy of the system. So that, if the scalar , then the nonlinear dynamical structure can be spontaneous one, otherwise the system requires some portion of energy to create a structure at , while  represents some indifferent case.

Note that the set (1) can be formally rewritten as

(2) ,

where  is a vector function. Using the polar coordinates , eqs. (2) read the following standard form

(3) ; ,

where . In most practical problems the vector function  appears as a power series in . This allows one to apply procedures of the normal transformations and the asymptotic methods of investigations.

Parametric approach

As an illustrative example we consider the so-called Bernoulli-Euler model governing the motion of a thin bar, according the following equations [3]:

(4)

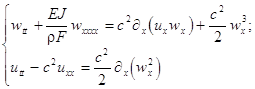
with the boundary conditions

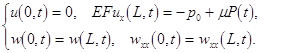
By scaling the sought variables:  and , eqs. (4) are reduced to a standard form (0).

Notice that the validity range of the model is associated with the wave velocities that should not exceed at least the characteristic speed . In the case of infinitesimal oscillations this set represents two uncoupled linear differential equations. Let , then the linearized equation for longitudinal displacements possesses a simple wave solution

,

where the frequencies  are coupled with the wave numbers  through the dispersion relation . Notice that . In turn, the linearized equation for bending oscillations reads[3]

(5) .

As one can see the right-hand term in eq. (5) contains a spatio-temporal parameter in the form of a standing wave. Allowances for the this wave-like parametric excitation become principal, if the typical velocity of longitudinal waves is comparable with the group velocities of bending waves, otherwise one can restrict consideration, formally assuming that  or , to the following simplest model:

(6) ,

which takes into account the temporal parametric excitation only.

We can look for solutions to eq. (5), using the Bubnov-Galerkin procedure:

,

where  denote the wave numbers of bending waves;  are the wave amplitudes defined by the ordinary differential equations

(7) .

Here

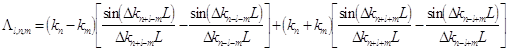
stands for a coefficient containing parameters of the wave-number detuning: , which, in turn, cannot be zeroes;  are the cyclic frequencies of bending oscillations at ;  denote the critical values of Euler forces.

Equations (7) describe the early evolution of waves at the expense of multi-mode parametric interaction. There is a key question on the correlation between phase orbits of the system (7) and the corresponding linearized subset

(8) ,

which results from eqs. (7) at . In other words, how effective is the dynamical response of the system (7) to the small parametric excitation?

First, we rewrite the set (7) in the equivalent matrix form: , where is the vector of solution,  denotes the  matrix of eigenvalues,  is the  matrix with quasi-periodic components at the basic frequencies . Following a standard method of the theory of ordinary differential equations, we look for a solution to eqs. (7) in the same form as to eqs. (8), where the integration constants should to be interpreted as new sought variables, for instance , where  is the vector of the nontrivial oscillatory solution to the uniform equations (8), characterized by the set of basic exponents . By substituting the ansatz  into eqs. (7), we obtain the first-order approximation equations in order :

.

where the right-hand terms are a superposition of quasi-periodic functions at the combinational frequencies . Thus the first-order approximation solution to eqs. (7) should be a finite quasi-periodic function [4], when the combinations ; otherwise, the problem of small divisors (resonances) appears.

So, one can continue the asymptotic procedure in the non-resonant case, i. e. , to define the higher-order correction to solution[5]. In other words, the dynamical perturbations of the system are of the same order as the parametric excitation. In the case of resonance the solution to eqs. (7) cannot be represented as convergent series in . This means that the dynamical response of the system can be highly effective even at the small parametric excitation.

In a particular case of the external force , eqs. (7) can be highly simplified:

(9)

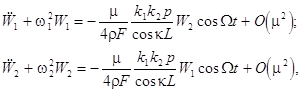
provided a couple of bending waves, having the wave numbers  and , produces both a small wave-number detuning  (i. e. ) and a small frequency detuning  (i. e. ). Here the symbols  denote the higher-order terms of order , since the values of  and  are also supposed to be small. Thus, the expressions

;

can be interpreted as the phase matching conditions creating a triad of waves consisting of the primary high-frequency longitudinal wave, directly excited by the external force , and the two secondary low-frequency bending waves parametrically excited by the standing longitudinal wave.

Notice that in the limiting model (6) the corresponding set of amplitude equations is reduced just to the single pendulum-type equation frequently used in many applications:

It is known that this equation can possess unstable solutions at small values of  and .

Solutions to eqs. (7) can be found using iterative methods of slowly varying phases and amplitudes:

(10) ; ,

where  and  are new unknown coordinates.

By substituting this into eqs. (9), we obtain the first-order approximation equations

(11) ; ,

where  is the coefficient of the parametric excitation;  is the generalized phase governed by the following differential equation

.

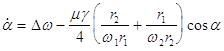Equations (10) and (11), being of a Hamiltonian structure, possess the two evident first integrals

 and ,

which allows one to integrate the system analytically. At , there exist quasi-harmonic stationary solutions to eqs. (10), (11), as

,

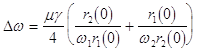which forms the boundaries in the space of system parameters within the first zone of the parametric instability.

From the physical viewpoint, one can see that the parametric excitation of bending waves appears as a degenerated case of nonlinear wave interactions. It means that the study of resonant properties in nonlinear elastic systems is of primary importance to understand the nature of dynamical instability, even considering free nonlinear oscillations.

Normal forms

The linear subset of eqs. (0) describes a superposition of harmonic waves characterized by the dispersion relation

,

where  refer the  branches of the natural frequencies depending upon wave vectors . The spectrum of the wave vectors and the eigenfrequencies can be both continuous and discrete one that finally depends upon the boundary and initial conditions of the problem. The normalization of the first order, through a special invertible linear transform

leads to the following linearly uncoupled equations

,

where the  matrix  is composed by -dimensional polarization eigenvectors  defined by the characteristic equation

;

 is the  diagonal matrix of differential operators with eigenvalues ;  and  are reverse matrices.

The linearly uncoupled equations can be rewritten in an equivalent matrix form [5]

(12)  and ,

using the complex variables . Here  is the  unity matrix. Here  is the -dimensional vector of nonlinear terms analytical at the origin . So, this can be presented as a series in , i. e.

,

where  are the vectors of homogeneous polynomials of degree , e. g.

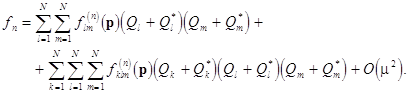
Here and  are some given differential operators. Together with the system (12), we consider the corresponding linearized subset

(13)  and ,

whose analytical solutions can be written immediately as a superposition of harmonic waves

,

where  are constant complex amplitudes;  is the number of normal waves of the -th type, so that  (for instance, if the operator  is a polynomial, then , where  is a scalar,  is a constant vector,  is some differentiable function. For more detail see [6]).

A question is following. What is the difference between these two systems, or in other words, how the small nonlinearity is effective?

According to a method of normal forms (see for example [7,8]), we look for a solution to eqs. (12) in the form of a quasi-automorphism, i. e.

(14)

where  denotes an unknown -dimensional vector function, whose components  can be represented as formal power series in , i. e. a quasi-bilinear form:

(15) ,

for example

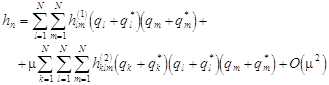
where  and  are unknown coefficients which have to be determined.

By substituting the transform (14) into eqs. (12), we obtain the following partial differential equations to define :

(16) .

It is obvious that the eigenvalues of the operator  acting on the polynomial components of  (i. e. ) are the linear integer-valued combinational values of the operator  given at various arguments of the wave vector .

In the lowest-order approximation in  eqs. (16) read

.

The polynomial components of  are associated with their eigenvalues , i. e. , where

or ,

while  in the lower-order approximation in .

So, if at least the one eigenvalue of  approaches zero, then the corresponding coefficient of the transform (15) tends to infinity. Otherwise, if , then  represents the lowest term of a formal expansion in .

Analogously, in the second-order approximation in :

the eigenvalues of  can be written in the same manner, i. e. , where , etc.

By continuing the similar formal iterations one can define the transform (15). Thus, the sets (12) and (13), even in the absence of eigenvalues equal to zeroes, are associated with formally equivalent dynamical systems, since the function  can be a divergent function. If  is an analytical function, then these systems are analytically equivalent. Otherwise, if the eigenvalue  in the -order approximation, then eqs. (12) cannot be simply reduced to eqs. (13), since the system (12) experiences a resonance.

For example, the most important 3-order resonances include

triple-wave resonant processes, when  and ;

generation of the second harmonic, as  and .

The most important 4-order resonant cases are the following:

four-wave resonant processes, when ;  (interaction of two wave couples); or when  and  (break-up of the high-frequency mode into tree waves);

degenerated triple-wave resonant processes at  and ;

generation of the third harmonic, as  and .

These resonances are mainly characterized by the amplitude modulation, the depth of which increases as the phase detuning approaches to some constant (e. g. to zero, if consider 3-order resonances). The waves satisfying the phase matching conditions form the so-called resonant ensembles.

Finally, in the second-order approximation, the so-called “non-resonant" interactions always take place. The phase matching conditions read the following degenerated expressions

cross-interactions of a wave pair at  and ;

self-action of a single wave as  and .

Non-resonant coupling is characterized as a rule by a phase modulation.

The principal proposition of this section is following. If any nonlinear system (12) does not have any resonance, beginning from the order  up to the order  , then the nonlinearity produces just small corrections to the linear field solutions. These corrections are of the same order that an amount of the nonlinearity up to times .

To obtain a formal transform (15) in the resonant case, one should revise a structure of the set (13) by modifying its right-hand side:

(16) ; ,

where the nonlinear terms . Here  are the uniform -th order polynomials. These should consist of the resonant terms only. In this case the eqs. (16) are associated with the so-called normal forms.

Remarks

In practice the series  are usually truncated up to first - or second-order terms in .

The theory of normal forms can be simply generalized in the case of the so-called essentially nonlinear systems, since the small parameter  can be omitted in the expressions (12) - (16) without changes in the main result. The operator  can depend also upon the spatial variables .

Formally, the eigenvalues of operator  can be arbitrary complex numbers. This means that the resonances can be defined and classified even in appropriate nonlinear systems that should not be oscillatory one (e. g. in the case of evolution equations).

Resonance in multi-frequency systems

The resonance plays a principal role in the dynamical behavior of most physical systems. Intuitively, the resonance is associated with a particular case of a forced excitation of a linear oscillatory system. The excitation is accompanied with a more or less fast amplitude growth, as the natural frequency of the oscillatory system coincides with (or sufficiently close to) that of external harmonic force. In turn, in the case of the so-called parametric resonance one should refer to some kind of comparativeness between the natural frequency and the frequency of the parametric excitation. So that, the resonances can be simply classified, according to the above outlined scheme, by their order, beginning from the number first , if include in consideration both linear and nonlinear, oscillatory and non-oscillatory dynamical systems.

For a broad class of mechanical systems with stationary boundary conditions, a mathematical definition of the resonance follows from consideration of the average functions

(17) 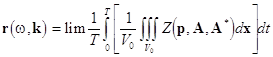, as ,

where  are the complex constants related to the linearized solution of the evolution equations (13);  denotes the whole spatial volume occupied by the system. If the function  has a jump at some given eigen values of and , then the system should be classified as resonant one[6]. It is obvious that we confirm the main result of the theory of normal forms. The resonance takes place provided the phase matching conditions

 and .

are satisfied. Here  is a number of resonantly interacting quasi-harmonic waves;  are some integer numbers ; and  are small detuning parameters. Example 1. Consider linear transverse oscillations of a thin beam subject to small forced and parametric excitations according to the following governing equation

,

where , , , , ,  è  are some appropriate constants, . This equation can be rewritten in a standard form

,

where , , . At , a solution this equation reads , where the natural frequency satisfies the dispersion relation . If , then slow variations of amplitude satisfy the following equation

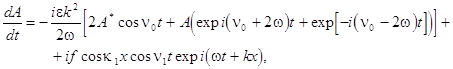
where , denotes the group velocity of the amplitude envelope. By averaging the right-hand part of this equation according to (17), we obtain

, at ;

, at  and ;

 in any other case.

Notice, if the eigen value of  approaches zero, then the first-order resonance always appears in the system (this corresponds to the critical Euler force).

The resonant properties in most mechanical systems with time-depending boundary conditions cannot be diagnosed by using the function .

Example 2. Consider the equations (4) with the boundary conditions ; ; . By reducing this system to a standard form and then applying the formula (17), one can define a jump of the function  provided the phase matching conditions

 è .

are satisfied. At the same time the first-order resonance, experienced by the longitudinal wave at the frequency , cannot be automatically predicted.

References

1.         Nelson DF, (1979), Electric, Optic and Acoustic Interactions in Dielectrics, Wiley-Interscience, NY.

2.         Kaup P. J., Reiman A. and Bers A. Space-time evolution of nonlinear three-wave interactions. Interactions in a homogeneous medium, Rev. of Modern Phys., (1979) 51 (2), 275-309.

3.         Kauderer H (1958), Nichtlineare Mechanik, Springer, Berlin.

4.         Haken H. (1983), Advanced Synergetics. Instability Hierarchies of Self-Organizing Systems and devices, Berlin, Springer-Verlag.

5.         Kovriguine DA, Potapov AI (1996), Nonlinear wave dynamics of 1D elastic structures, Izvestiya vuzov. Appl. Nonlinear Dynamics, 4 (2), 72-102 (in Russian).

6.         Maslov VP (1973), Operator methods, Moscow, Nauka publisher (in Russian).

7.         Jezequel L., Lamarque C. - H. Analysis of nonlinear dynamical systems by the normal form theory, J. of Sound and Vibrations, (1991) 149 (3), 429-459.

8.         Pellicano F, Amabili M. and Vakakis AF (2000), Nonlinear vibration and multiple resonances of fluid-filled, circular shells, Part 2: Perturbation analysis, Vibration and Acoustics, 122, 355-364.

9.         Zhuravlev VF and Klimov DM (1988), Applied methods in the theory of oscillations, Moscow, Nauka publisher (in Russian)

[1] The small parameter  can also characterize an amount of small damped forced and/or parametric excitation, etc.

[2] The discrete part of the spectrum can be represented as a sum of delta-functions, i.e. .

[3] The resonance appears in the system as  that corresponds to any integer number of quarters of wavelengths. There is no stationary solution in the form of standing waves in this case, though the resonant solution for longitudinal waves can be simply designed using the d'Alambert approach.

[4]The conservation of quasi-periodic orbits represents a forthcoming mathematical problem in mathematics, which is in progress up to now [4].

[5] Practically, the resonant properties should be directly associated with the order of the approximation procedure. For instance, if the first-order approximation is considered, then the resonances in order  have to be neglected.

[6] In applied problems the definition of resonance should be directly associated with the order of the approximation procedure. For instance, if the first-order approximation is considered, then the jupms of  of order  have to be neglected [9].