Дипломная работа: Triple-wave ensembles in a thin cylindrical shell

TRIPLE-WAVE ENSEMBLES IN A THIN CYLINDRICAL SHELL

Kovriguine DA, Potapov AI

Introduction

Primitive nonlinear quasi-harmonic triple-wave patterns in a thin-walled cylindrical shell are investigated. This task is focused on the resonant properties of the system. The main idea is to trace the propagation of a quasi-harmonic signal — is the wave stable or not? The stability prediction is based on the iterative mathematical procedures. First, the lowest-order nonlinear approximation model is derived and tested. If the wave is unstable against small perturbations within this approximation, then the corresponding instability mechanism is fixed and classified. Otherwise, the higher-order iterations are continued up to obtaining some definite result.

The theory of thin-walled shells based on the Kirhhoff-Love hypotheses is used to obtain equations governing nonlinear oscillations in a shell. Then these equations are reduced to simplified mathematical models in the form of modulation equations describing nonlinear coupling between quasi-harmonic modes. Physically, the propagation velocity of any mechanical signal should not exceed the characteristic wave velocity inherent in the material of the plate. This restriction allows one to define three main types of elemental resonant ensembles — the triads of quasi-harmonic modes of the following kinds:

(i) high-frequency longitudinal and two low-frequency bending waves (-type triads);

(ii)high-frequency shear and two low-frequency bending waves ();

(iii)high-frequency bending, low-frequency bending and shear waves ();

(iv)high-frequency bending and two low-frequency bending waves ().

Here subscripts identify the type of modes, namely () — longitudinal, () — bending, and () — shear mode. The first one stands for the primary unstable high-frequency mode, the other two subscripts denote secondary low-frequency modes.

Triads of the first three kinds (i — iii) can be observed in a flat plate (as the curvature of the shell goes to zero), while the -type triads are inherent in cylindrical shells only.

Notice that the known Karman-type dynamical governing equations can describe the -type triple-wave coupling only. The other triple-wave resonant ensembles, ,  and , which refer to the nonlinear coupling between high-frequency shear (longitudinal) mode and low-frequency bending modes, cannot be described by this model.

Quasi-harmonic bending waves, whose group velocities do not exceed the typical propagation velocity of shear waves, are stable against small perturbations within the lowest-order nonlinear approximation analysis. However amplitude envelopes of these waves can be unstable with respect to small long-wave perturbations in the next approximation. Generally, such instability is associated with the degenerated four-wave resonant interactions. In the present paper the second-order approximation effects is reduced to consideration of the self-action phenomenon only. The corresponding mathematical model in the form of Zakharov-type equations is proposed to describe such high-order nonlinear wave patterns.

Governing equations

We consider a deformed state of a thin-walled cylindrical shell of the length , thickness , radius , in the frame of references . The -coordinate belongs to a line beginning at the center of curvature, and passing perpendicularly to the median surface of the shell, while  and  are in-plane coordinates on this surface (). Since the cylindrical shell is an axisymmetric elastic structure, it is convenient to pass from the actual frame of references to the cylindrical coordinates, i.e. , where  and . Let the vector of displacements of a material point lying on the median surface be . Here ,  and  stand for the longitudinal, circumferential and transversal components of displacements along the coordinates  and , respectively, at the time . Then the spatial distribution of displacements reads

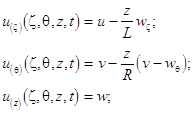
accordingly to the geometrical paradigm of the Kirhhoff-Love hypotheses. From the viewpoint of further mathematical rearrangements it is convenient to pass from the physical sought variables  to the corresponding dimensionless displacements . Let the radius and the length of the shell be comparable values, i.e. , while the displacements be small enough, i.e. . Then the components of the deformation tensor can be written in the form

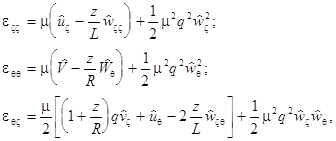
where  is the small parameter; ;  and . The expression for the spatial density of the potential energy of the shell can be obtained using standard stress-straight relationships accordingly to the dynamical part of the Kirhhoff-Love hypotheses:

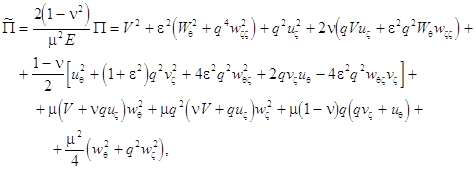
where  is the Young modulus;  denotes the Poisson ratio;  (the primes indicating the dimensionless variables have been omitted). Neglecting the cross-section inertia of the shell, the density of kinetic energy reads

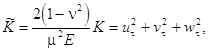
where  is the dimensionless time;  is typical propagation velocity.

Let the Lagrangian of the system be .

By using the variational procedures of mechanics, one can obtain the following equations governing the nonlinear vibrations of the cylindrical shell (the Donnell model):

(1)

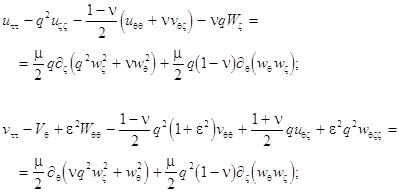
(2)

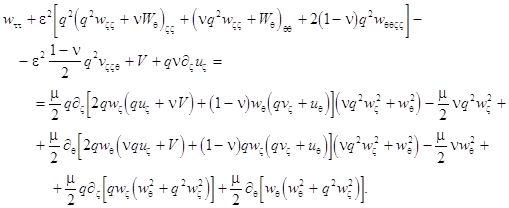
Equations (1) and (2) are supplemented by the periodicity conditions

Dispersion of linear waves

At  the linear subset of eqs.(1)-(2) describes a superposition of harmonic waves

(3)

Here  is the vector of complex-valued wave amplitudes of the longitudinal, circumferential and bending component, respectively;  is the phase, where  are the natural frequencies depending upon two integer numbers, namely  (number of half-waves in the longitudinal direction) and  (number of waves in the circumferential direction). The dispersion relation defining this dependence  has the form

(4)

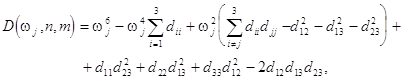
where

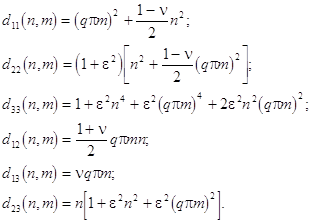
In the general case this equation possesses three different roots () at fixed values of  and . Graphically, these solutions are represented by a set of points occupied the three surfaces . Their intersections with a plane passing the axis of frequencies are given by fig.(1). Any natural frequency  corresponds to the three-dimensional vector of amplitudes . The components of this vector should be proportional values, e.g. , where the ratios

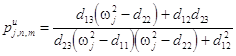
and

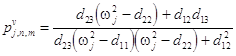
are obeyed to the orthogonality conditions

as  .

Assume that , then the linearized subset of eqs.(1)-(2) describes planar oscillations in a thin ring. The low-frequency branch corresponding generally to bending waves is approximated by  and , while the high-frequency azimuthal branch —  and . The bending and azimuthal modes are uncoupled with the shear modes. The shear modes are polarized in the longitudinal direction and characterized by the exact dispersion relation .

Consider now axisymmetric waves (as ). The axisymmetric shear waves are polarized by azimuth: , while the other two modes are uncoupled with the shear mode. These high- and low-frequency branches are defined by the following biquadratic equation

.

At the vicinity of  the high-frequency branch is approximated by

,

while the low-frequency branch is given by

.

Let , then the high-frequency asymptotic be

,

while the low-frequency asymptotic:

.

When neglecting the in-plane inertia of elastic waves, the governing equations (1)-(2) can be reduced to the following set (the Karman model):

(5)

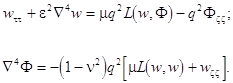
Here  and  are the differential operators;  denotes the Airy stress function defined by the relations ,  and , where , while ,  and  stand for the components of the stress tensor. The linearized subset of eqs.(5), at , is represented by a single equation

defining a single variable , whose solutions satisfy the following dispersion relation

(6)

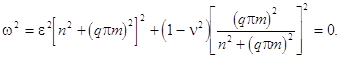
Notice that the expression (6) is a good approximation of the low-frequency branch defined by (4).

Evolution equations

If , then the ansatz (3) to the eqs.(1)-(2) can lead at large times and spatial distances, , to a lack of the same order that the linearized solutions are themselves. To compensate this defect, let us suppose that the amplitudes  be now the slowly varying functions of independent coordinates ,  and , although the ansatz to the nonlinear governing equations conserves formally the same form (3):

Obviously, both the slow  and the fast  spatio-temporal scales appear in the problem. The structure of the fast scales is fixed by the fast rotating phases (), while the dependence of amplitudes  upon the slow variables is unknown.

This dependence is defined by the evolution equations describing the slow spatio-temporal modulation of complex amplitudes.

There are many routs to obtain the evolution equations. Let us consider a technique based on the Lagrangian variational procedure. We pass from the density of Lagrangian function  to its average value

(7),

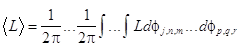An advantage of the transform (7) is that the average Lagrangian depends only upon the slowly varying complex amplitudes and their derivatives on the slow spatio-temporal scales ,  and . In turn, the average Lagrangian does not depend upon the fast variables.

The average Lagrangian  can be formally represented as power series in :

(8)

At  the average Lagrangian (8) reads

where the coefficient  coincides exactly with the dispersion relation (3). This means that .

The first-order approximation average Lagrangian  depends upon the slowly varying complex amplitudes and their first derivatives on the slow spatio-temporal scales ,  and . The corresponding evolution equations have the following form

(9)

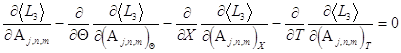
Notice that the second-order approximation evolution equations cannot be directly obtained using the formal expansion of the average Lagrangian , since some corrections of the term  are necessary. These corrections are resulted from unknown additional terms  of order , which should generalize the ansatz (3):

provided that the second-order approximation nonlinear effects are of interest.

Triple-wave resonant ensembles

The lowest-order nonlinear analysis predicts that eqs.(9) should describe the evolution of resonant triads in the cylindrical shell, provided the following phase matching conditions

(10),

hold true, plus the nonlinearity in eqs.(1)-(2) possesses some appropriate structure. Here  is a small phase detuning of order , i.e. . The phase matching conditions (10) can be rewritten in the alternative form

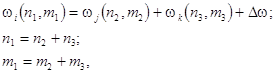
where  is a small frequency detuning;  and  are the wave numbers of three resonantly coupled quasi-harmonic nonlinear waves in the circumferential and longitudinal directions, respectively. Then the evolution equations (9) can be reduced to the form analogous to the classical Euler equations, describing the motion of a gyro:

(11).

Here  is the potential of the triple-wave coupling;  are the slowly varying amplitudes of three waves at the frequencies  and the wave numbers  and ; are the group velocities;  is the differential operator;  stand for the lengths of the polarization vectors ( and );  is the nonlinearity coefficient:

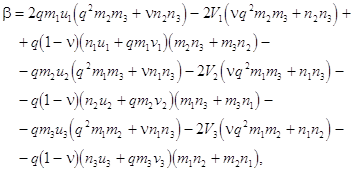
where .

Solutions to eqs.(11) describe four main types of resonant triads in the cylindrical shell, namely -, -, - and -type triads. Here subscripts identify the type of modes, namely () — longitudinal, () — bending, and () — shear mode. The first subscript stands for the primary unstable high-frequency mode, the other two subscripts denote the secondary low-frequency modes.

A new type of the nonlinear resonant wave coupling appears in the cylindrical shell, namely -type triads, unlike similar processes in bars, rings and plates. From the viewpoint of mathematical modeling, it is obvious that the Karman-type equations cannot describe the triple-wave coupling of -, - and -types, but the -type triple-wave coupling only. Since -type triads are inherent in both the Karman and Donnell models, these are of interest in the present study.

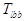-triads

High-frequency azimuthal waves in the shell can be unstable with respect to small perturbations of low-frequency bending waves. Figure (2) depicts a projection of the corresponding resonant manifold of the shell possessing the spatial dimensions:  and . The primary high-frequency azimuthal mode is characterized by the spectral parameters  and  (the numerical values of  and  are given in the captions to the figures). In the example presented the phase detuning does not exceed one percent. Notice that the phase detuning almost always approaches zero at some specially chosen ratios between  and , i.e. at some special values of the parameter. Almost all the exceptions correspond, as a rule, to the long-wave processes, since in such cases the parameter  cannot be small, e.g. .

NB Notice that -type triads can be observed in a thin rectilinear bar, circular ring and in a flat plate.

NBThe wave modes entering -type triads can propagate in the same spatial direction.

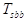-triads

Analogously, high-frequency shear waves in the shell can be unstable with respect to small perturbations of low-frequency bending waves. Figure (3) displays the projection of the -type resonant manifold of the shell with the same spatial sizes as in the previous subsection. The wave parameters of primary high-frequency shear mode are  and . The phase detuning does not exceed one percent. The triple-wave resonant coupling cannot be observed in the case of long-wave processes only, since in such cases the parameter  cannot be small.

NBThe wave modes entering -type triads cannot propagate in the same spatial direction. Otherwise, the nonlinearity parameter  in eqs.(11) goes to zero, as all the waves propagate in the same direction. This means that such triads are essentially two-dimensional dynamical objects.

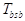-triads

High-frequency bending waves in the shell can be unstable with respect to small perturbations of low-frequency bending and shear waves. Figure (4) displays an example of projection of the -type resonant manifold of the shell with the same sizes as in the previous sections. The spectral parameters of the primary high-frequency bending mode are  and . The phase detuning also does not exceed one percent. The triple-wave resonant coupling can be observed only in the case when the group velocity of the primary high-frequency bending mode exceeds the typical velocity of shear waves.

NBEssentially, the spectral parameters of -type triads fall near the boundary of the validity domain predicted by the Kirhhoff-Love theory. This means that the real physical properties of -type triads can be different than theoretical ones.

NB-type triads are essentially two-dimensional dynamical objects, since the nonlinearity parameter goes to zero, as all the waves propagate in the same direction.

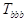-triads

High-frequency bending waves in the shell can be unstable with respect to small perturbations of low-frequency bending waves. Figure (5) displays an example of the projection of the -type resonant manifold of the shell with the same sizes as in the previous sections. The wave parameters of the primary high-frequency bending mode are  and . The phase detuning does not exceed one percent. The triple-wave resonant coupling cannot also be observed only in the case of long-wave processes, since in such cases the parameter  cannot be small.

NBThe resonant interactions of -type are inherent in cylindrical shells only.

Manly-Rawe relations

By multiplying each equation of the set (11) with the corresponding complex conjugate amplitude and then summing the result, one can reduce eqs.(11) to the following divergent laws

(12)

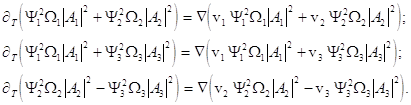
Notice that the equations of the set (12) are always linearly dependent. Moreover, these do not depend upon the nonlinearity potential . In the case of spatially uniform wave processes () eqs.(12) are reduced to the well-known Manly-Rawe algebraic relations

(13)

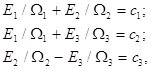
where  are the portion of energy stored by the quasi-harmonic mode number ;  are the integration constants dependent only upon the initial conditions. The Manly-Rawe relations (13) describe the laws of energy partition between the modes of the triad. Equations (13), being linearly dependent, can be always reduced to the law of energy conservation

(14).

Equation (14) predicts that the total energy of the resonant triad is always a constant value , while the triad components can exchange by the portions of energy , accordingly to the laws (13). In turn, eqs.(13)-(14) represent the two independent first integrals to the evolution equations (11) with spatially uniform initial conditions. These first integrals describe an unstable hyperbolic orbit behavior of triads near the stationary point , or a stable motion near the two stationary elliptic points , and .

In the case of spatially uniform dynamical processes eqs.(11), with the help of the first integrals, are integrated in terms of Jacobian elliptic functions [1,2]. In the particular case, as  or , the general analytic solutions to eqs.(11), within an appropriate Cauchy problem, can be obtained using a technique of the inverse scattering transform [3]. In the general case eqs.(11) cannot be integrated analytically.

Break-up instability of axisymmetric waves

Stability prediction of axisymmetric waves in cylindrical shells subject to small perturbations is of primary interest, since such waves are inherent in axisymmetric elastic structures. In the linear approximation the axisymmetric waves are of three types, namely bending, shear and longitudinal ones. These are the axisymmetric shear waves propagating without dispersion along the symmetry axis of the shell, i.e. modes polarized in the circumferential direction, and linearly coupled longitudinal and bending waves.

It was established experimentally and theoretically that axisymmetric waves lose the symmetry when propagating along the axis of the shell. From the theoretical viewpoint this phenomenon can be treated within several independent scenarios.

The simplest scenario of the dynamical instability is associated with the triple-wave resonant coupling, when the high-frequency mode breaks up into some pairs of secondary waves. For instance, let us suppose that an axisymmetric quasi-harmonic longitudinal wave ( and ) travels along the shell. Figure (6) represents a projection of the triple-wave resonant manifold of the shell, with the geometrical sizes  m;  m;  m, on the plane of wave numbers. One can see the appearance of six secondary wave pairs nonlinearly coupled with the primary wave. Moreover, in the particular case the triple-wave phase matching is reduced to the so-called resonance 2:1. This one can be proposed as the main instability mechanism explaining some experimentally observed patterns in shells subject to periodic cinematic excitations [4].

It was pointed out in the paper [5] that the resonance 2:1 is a rarely observed in shells. The so-called resonance 1:1 was proposed instead as the instability mechanism. This means that the primary axisymmetric mode (with ) can be unstable one with respect to small perturbations of the asymmetric mode (with ) possessing a natural frequency closed to that of the primary one. From the viewpoint of theory of waves this situation is treated as the degenerated four-wave resonant interaction.

In turn, one more mechanism explaining the loss of stability of axisymmetric waves in shells based on a paradigm of the so-called nonresonant interactions can be proposed [6,7,8]. By the way, it was underlined in the paper [6] that theoretical prognoses relevant to the modulation instability are extremely sensible upon the model explored. This means that the Karman-type equations and Donnell-type equations lead to different predictions related the stability properties of axisymmetric waves.

Self-action

The propagation of any intense bending waves in a long cylindrical shell is accompanied by the excitation of long-wave displacements related to the in-plane tensions and rotations. In turn, these long-wave fields can influence on the theoretically predicted dependence between the amplitude and frequency of the intense bending wave.

Moreover, quasi-harmonic bending waves, whose group velocities do not exceed the typical propagation velocity of shear waves, are stable against small perturbations within the lowest-order nonlinear approximation analysis. However amplitude envelopes of these waves can be unstable with respect to small long-wave perturbations in the next approximation.

Amplitude-frequency curve

Let us consider a stationary wave

traveling along the single direction characterized by the ''companion'' coordinate . By substituting this expression into the first and second equations of the set (1)-(2), one obtains the following differential relations

(15)

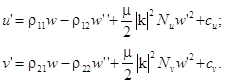
Here

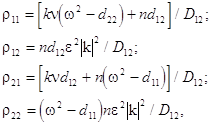
while

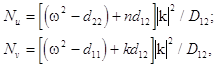
where and .

Using (15) one can get the following nonlinear ordinary differential equation of the fourth order:

(16),

which describes simple stationary waves in the cylindrical shell (primes denote differentiation). Here

where and  are the integration constants.

If the small parameter , and , ,  satisfies the dispersion relation (4), then a periodic solution to the linearized equation (16) reads

where  are arbitrary constants, since .

Let the parameter  be small enough, then a solution to eq.(16) can be represented in the following form

(17)

where the amplitude  depends upon the slow variables , while  are small nonresonant corrections. After the substitution (17) into eq.( 16) one obtains the expression of the first-order nonresonant correction

and the following modulation equation

(18),

where the nonlinearity coefficient is given by

.

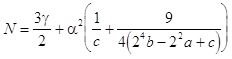Suppose that the wave vector  is conserved in the nonlinear solution. Taking into account that the following relation

holds true for the stationary waves, one gets the following modulation equation instead of eq.(18):

or

,

where the point denotes differentiation on the slow temporal scale . This equation has a simple solution for spatially uniform and time-periodic waves of constant amplitude :

,

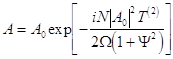which characterizes the amplitude-frequency response curve of the shell or the Stocks addition to the natural frequency of linear oscillations:

(19).

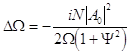Spatio-temporal modulation of waves

Relation (19) cannot provide information related to the modulation instability of quasi-harmonic waves. To obtain this, one should slightly modify the ansatz (17):

(20)

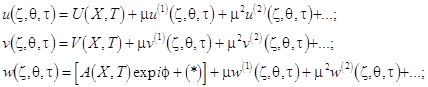
where  and  denote the long-wave slowly varying fields being the functions of arguments  and  (these turn in constants in the linear theory);  is the amplitude of the bending wave; ,  and  are small nonresonant corrections. By substituting the expression (20) into the governing equations (1)-(2), one obtains, after some rearranging, the following modulation equations

(21)

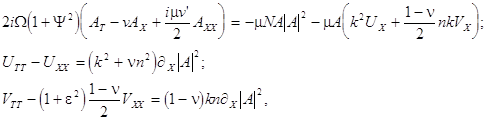
where  is the group velocity, and . Notice that eqs.(21) have a form of Zakharov-type equations.

Consider the stationary quasi-harmonic bending wave packets. Let the propagation velocity be , then eqs.(21) can be reduced to the nonlinear Schrцdinger equation

(22),

where the nonlinearity coefficient is equal to

,

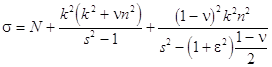while the non-oscillatory in-plane wave fields are defined by the following relations

and

.

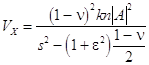The theory of modulated waves predicts that the amplitude envelope of a wavetrain governed by eq.(22) will be unstable one provided the following Lighthill criterion

(23)

is satisfied.

Envelope solitons

The experiments described in the paper [7] arise from an effort to uncover wave systems in solids which exhibit soliton behavior. The thin open-ended nickel cylindrical shell, having the dimensions cm,  cm and  cm, was made by an electroplating process. An acoustic beam generated by a horn driver was aimed at the shell. The elastic waves generated were flexural waves which propagated in the axial, , and circumferential, , direction. Let  and , respectively, be the eigen numbers of the mode. The modes in which  is always one and  ranges from 6 to 32 were investigated. The only modes which we failed to excite (for unknown reasons) were = 9,10,19. A flexural wave pulse was generated by blasting the shell with an acoustic wave train typically 15 waves long. At any given frequency the displacement would be given by a standing wave component and a traveling wave component. If the pickup transducer is placed at a node in the standing wave its response will be limited to the traveling wave whose amplitude is constant as it propagates.

The wave pulse at frequency of 1120 Hz was generated. The measured speed of the clockwise pulse was 23 m/s and that of the counter-clockwise pulse was 26 m/s, which are consistent with the value calculated from the dispersion curve (6) within ten percents. The experimentally observed bending wavetrains were best fitting plots of the theoretical hyperbolic functions, which characterizes the envelope solitons. The drop in amplitude, in 105/69 times, was believed due to attenuation of the wave. The shape was independent of the initial shape of the input pulse envelope.

The agreement between the experimental data and the theoretical curve is excellent. Figure 7 displays the dependence of the nonlinearity coefficient  and eigen frequencies  versus the wave number  of the cylindrical shell with the same geometrical dimensions as in the work [7]. Evidently, the envelope solitons in the shell should arise accordingly to the Lighthill criterion (23) in the range of wave numbers =6,7,..,32, as .

REFERENCES

[1]Bretherton FP (1964), Resonant interactions between waves, J. Fluid Mech., 20, 457-472.

[2]Bloembergen K. (1965), Nonlinear optics, New York-Amsterdam.

[3]Ablowitz MJ, H Segur (1981), Solitons and the Inverse Scattering Transform, SIAM, Philadelphia.

[4]Kubenko VD, Kovalchuk PS, Krasnopolskaya TS (1984), Nonlinear interaction of flexible modes of oscillation in cylindrical shells, Kiev: Naukova dumka publisher (in Russian).

[5]Ginsberg JM (1974), Dynamic stability of transverse waves in circular cylindrical shell, Trans. ASME J. Appl. Mech., 41(1), 77-82.

[6]Bagdoev AG, Movsisyan LA (1980), Equations of modulation in nonlinear dispersive media and their application to waves in thin bodies, .Izv. AN Arm.SSR, 3, 29-40 (in Russian).

[7]Kovriguine DA, Potapov AI (1998), Nonlinear oscillations in a thin ring - I(II), Acta Mechanica, 126, 189-212.