Дипломная работа: Активізація пізнавальної діяльності учнів в процесі навчання математики
Раздел: Рефераты по педагогике
Тип: дипломная работа
ЗМІСТ
Вступ
Розділ 1. Теоретичні основи активізації пізнавальної діяльності учнів 9 класу основної школи в процесі навчання математики
1.1 Зміст та основні положення активізації пізнавальної діяльності школярів
1.2 Математичні задачі фінансового змісту як засіб активізації пізнавальної діяльності учнів
1.3 Психолого-методичні основи активізації пізнавальної діяльності учнів основної школи під час навчання математики
1.3.1 Психологічні основи активізації пізнавальної діяльності учнів підліткового віку
1.3.2 Методи, засоби та прийоми активізації пізнавальної діяльності учнів у процесі розв’язування математичних задач фінансового змісту
Розділ 2. Методичні рекомендації щодо використання математичних задач фінансового змісту для активізації пізнавальної діяльності учнів
2.1 Використання задач на банківські розрахунки в основній школі.
2.2 Особливості роботи із задачами на оподаткування
2.3 Місце задач на цінні папери в курсі математики основної школи
2.4 Методичні рекомендації використання задач на сімейний бюджет
2.5 Задачі на страхування та їх особливості
2.6 Організація, проведення та аналіз результатів педагогічного експерименту
Висновки
Список використаних джерел
Додатки
ВСТУП
Актуальність дослідження. Національна доктрина розвитку освіти в Україні та Концепція загальної середньої освіти (12-річна школа) спрямовують педагогічну науку на пошук нових принципів та критеріїв вибору змісту освіти, нових технологій, які ведуть до високої теоретичної та практичної підготовки учня та орієнтовані на розвиток особистості. Нові досягнення створюють більш сприятливі умови для отримання кожним учнем можливого рівня математичних знань та загального розвитку.
Економічні чинники сьогоднішнього суспільства вимагають від людини, яка починає самостійне життя, володіти набором практичних знань, вмінь та навичок з фінансової науки, що можливе за умови опанування шкільним курсом математики. Держава, згідно з Конституцією України, надає можливість кожній людині мати право на вільний розвиток своєї особистості... "Кожен має право на підприємницьку діяльність, яка не заборонена законом." [32 , cт. 42] Для цього необхідні освічені люди в економічній галузі, які зможуть як теоретично, так і практично впроваджувати в життя різні аспекти фінансової діяльності. Саме розвиток людини як найважливішої суспільної цінності приводить до змін у освітній сфері.
Від пізнавальної активності учнів під час вивчення шкільного курсу математики залежать результати знань, їх підготовка до роботи в сучасних умовах, до творчої діяльності. Цей факт потребує реалізації методів навчання, спрямованих на підвищення пізнавальної діяльності школярів у оволодінні знаннями, розвитку їх навичок до самоосвіти та його творчого використання в нових життєвих умовах. Саме через активну творчу діяльність можна досягти міцного засвоєння та усвідомлення навчального матеріалу, розвитку навичок його творчого використання.
Активізація пізнавальної діяльності учнів є багатоаспектним питанням. Ії характерними рисами є підвищення рівня активності та самостійності учнів, незмінно зростаючі працездатність та інтерес учнів до математики. Це можливе завдяки вдосконаленню змісту запропонованого для вивчення матеріалу, подання його в зрозумілішій для учнів формі, де відображається практичне значення явищ та фактів, що вивчаються. Такі завдання спонукають учнів застосовувати отримані знання в життєво-практичних ситуаціях та виробляють в них необхідні в житті уміння та навички.
Важливою є допомога школи у виробленні самостійності мислення, вмінні приймати рішення, застосуванні теоретичних знань в повсякденному житті. У зв’язку з цим постає питання про вдосконалення методів та прийомів навчання математики, які спроможні максимально сприяти розвитку активного та самостійного навчання учнів. Одним з основних чинників підвищення ефективності навчання є керівництво процесом знань, яке сприяє пробудженню думки та почуттів учнів.
У даному контексті виникає питання про формування особистості, здатної знаходити, оцінювати та використовувати отриману інформацію, а також застосовувати набуті знання в різних сферах діяльності.
Важливою умовою активізації пізнавальної діяльності учнів в процесі навчання є знання психологічних закономірностей розвитку школярів. Це можна відмітити в працях Б.Г. Ананьєва [1], О.М. Кабанової-Меллер [29], В.О. Крутецького [36], П.Д. Кудрявцева [36], Н.О. Менчинської [41], С.Л. Рубінштейна [51] та інших.
В існуючих наукових дослідженнях розглядаються питання формування пізнавальної активності, показано її природу та сутність, проведено аналіз рівнів пізнавальної активності (Л.П. Аристова [2], Т.В. Габай [11], Т.Г. Шамова [62], Г.І. Щукіна [65;66]).
У практиці навчання математики більше спостерігається прояв інтересу учнів до розв‘язання задач прикладного спрямування, ніж до теоретичних чи тренувальних вправ. І це не випадково. В таких задачах розглядається певна реальна ситуація, яка вчить не лише математичним законам, а й показує їх практичне застосування. Тому потрібно, щоб вивчення математики включало в себе більше задач практичного значення. Вони зацікавлюють учнів, показують можливість реалізації математичних знань в життєвих ситуаціях [54,c.3].
Математика дає методи розв‘язання економічних та фінансових задач. Вона також є важливим елементом загальної культури населення. Відтак математичні знання слід розглядати як складову в системі фундаментальної освіти майбутніх громадян держави, зокрема їх фінансової освіти. Математичні задачі фінансового змісту - це засіб ознайомлення учнів з застосуванням математичних понять та методів у фінансовій галузі та розкриття можливостей математики у фінансовій теорії.
Зв’язок математичних знань з життям створює нові умови для розвитку пізнавальної діяльності учнів. Це значно розширює межі навчання, додає, поряд з основами математики, знання фінансової термінології, бюджетних відносин, грошового обігу, формування та отримання прибутку. Це також формує передумови для підготовки учнів до виконання визначених соціальних функцій у відповідності до тенденцій трансформації суспільства та розвитку особистості в умовах ринкових відносин.
Робота з прикладними задачами фінансового змісту в процесі навчання математики сприяє, з одного боку, розвитку математичного мислення, зацікавлює учнів, а з іншого – озброює їх фінансовими знаннями. Це відбувається завдяки математичним інтерпретаціям фінансових понять, які використовуються в процесі розв’язання задач.
Наведені міркування обумовили вибір теми та актуальність дипломного дослідження, яка формулюється наступним чином: "Активізація пізнавальної діяльності учнів 9 класу в процесі розв’язування математичних задач фінансового змісту".
Об'єктом дослідження є процес навчання математики в основній школі.
Предмет дослідження – розробка системи математичних задач фінансового змісту в навчальному процесі як засіб активізації пізнавальної діяльності учнів основної школи.
Мета дослідлження полягає у створенні окремих елементів системи математичних задач фінансового змісту, орієнтованої на активізацію пізнавальної діяльності учнів 9 класу основної школи під час навчання їх математики. Гіпотеза дослідження: якщо створити систему математичних задач фінансового змісту для курсу математики основної школи, впровадити її в навчальний процес, то це стане вагомим чинником для:
- формування пізнавального інтересу учнів до вивчення математики;
- підвищення успішності та якості математичної підготовки учнів;
- формування в учнів знань, вмінь та навичок використання математичних знань в фінансовій сфері практичної діяльності;
- розвитку логічного мислення, творчої активності та пізнавальної самостійності школярів.
Поставлена мета та робоча гіпотеза обумовили необхідність вирішення таких завдань дослідження:
1. Обґрунтувати психолого-методичні основи активізації пізнавальної діяльності учнів основної школи в процесі розв’язування математичних задач фінансового змісту.
2. З’ясувати можливості вдосконалення навчального процесу з математики та підвищення якості його результатів за рахунок використання математичних задач фінансового змісту.
3. Створити систему математичних задач фінансового змісту, яка сприяє активізації пізнавальної діяльності учнів.
4. Експериментально перевірити ефективність запропонованих системи задач, та їх вплив на формування пізнавального інтересу учнів до вивчення математики в основній школі.
РОЗДІЛ 1. Теоретичні основи активізації пізнавальної діяльності учнів основної школи в процесі навчання математики
1.1. Зміст та основні положення активізації пізнавальної діяльності школярів
Однією з актуальних проблем на сучасному етапі розвитку педагогічної теорії та практики є активізація пізнавальної діяльності учнів. Саме від її вирішення залежить ефективність навчальної діяльності, яка проявляється в міцному засвоєнні знань, стимулюванні та розвитку інтересу до навчання, формуванні самостійної думки та підготовці до самостійного життя.
У педагогічних дослідженнях найчастіше активізацію пізнавальної діяльності розглядають як організацію сприйняття навчального матеріалу учнями, коли засвоєння знань відбувається шляхом розкриття взаємозв'язку між явищами, порівняння нової інформації із вже відомою, а також конкретизації, узагальнення та оцінки навчального матеріалу з різних точок зору [48].
Зазначимо, що в педагогічному словнику активізацію навчального процесу визначено як процес удосконалення змісту, форм і методів навчальної роботи, що сприяє активній і самостійній діяльності учнів у засвоєнні знань, вмінь та навичок на всіх етапах навчально-виховного процесу у всіх ланках освіти [42]. В цьому сенсі акцентується важливість педагогічних методів, прийомів та засобів в процесі активізації.
Використання та удосконалення різних форм та методів навчання спонукає до активізації, в першу чергу, самого навчального процесу, а вже потім до активізації пізнавальної діяльності учнів. Варто зазначити, що в наведених вище означеннях відбувається ототожнення понять “активізація навчання” та “активізація пізнавальної діяльності”. В основі будь-якої навчальної діяльності учнів лежить, в першу чергу, їх активність. Процес їх активізації є процесом перетворення суб’єкта (в нашому випадку - учня) в стан активності. Поняття активності досліджувалось в психолого-педагогічній науці в різних аспектах. Термін “активність” походить з латинської “actives”, що означає діяльний, енергійний, ініціативний. В педагогічному словнику за редакцією М.Д.Ярмаченка наводиться таке визначення: “активність – 1) властивість організму і психіки, що залежить від зовнішніх та внутрішніх потреб; 2)властивість особистості, яка виявляється в діяльному ініціативному ставленні до навколишнього світу та самої себе [42, с.21]”.
Активність учнів виражається через запитання, прагнення думати, пізнавальну самостійність у процесах сприйняття, відтворення, розуміння та творчого застосування. Критеріями сформованості активності особистості виступають: ініціативність, дієвість, енергійність, інтенсивність, добросовісність, інтерес, самостійність, усвідомлення дій, воля, наполегливість в досягненні мети та творчість. Завдяки цим якостям є можливість простежити підвищення активності учнів в процесі навчання. Тому ми виділили такі рівні активності учня в навчальній діяльності:
1. Низький – вчитель повідомляє знання, ставить запитання, дає відповіді, показує способи розв’язання завдання, а учень слухає, записує та пригадує повідомлене.
2. Середній – завдання розв’язуються сумісними зусиллями вчителя та учнів; учні залучаються у частковий пошук, виявляючи при цьому епізодичний інтерес до роботи, елементи творчості, самостійності тощо.
3. Високий – учні самі здійснюють активний пошук відповіді, пропонують власні способи розв’язування завдань, виявляють стійкий інтерес, прагнення, добросовісне ставлення до роботи тощо.
Прояв активності в процесі навчання пов’язаний з пізнанням світу. Тому в багатьох педагогічних джерелах акцентується важливість саме пізнавальної активності, яка виникає завдяки продуктивній активності. Пізнавальна активність - складне інтегральне утворення особистості, що має мотиваційні, операційні та результативні компоненти. Серед них прояв інтелектуальної ініціативи, надситуативності - вихід особистості за межі даної діяльності за власним бажанням, прагнення до нового цілеутворення [42]. Відмінність пізнавальної активності від загальної активності полягає в тому, що “активність” як поняття включає не лише процес пізнання, а й інші сфери діяльності учня, зокрема вольову та емоційну.
Ознаками пізнавальної активності в будь-якій діяльності виступають такі показники, як готовність до роботи, прагнення до самостійної діяльності, якість роботи, шляхи вибору оптимальних способів розв’язання завдань.
Пізнавальна активність у навчальному процесі є складовою об’єктивного закономірного навчання як активного процесу пізнання. Це виступає важливим фактором необхідності активної діяльності учнів у пізнанні. Однак характер та ступінь активності учнів у навчанні можуть бути різними. Які ж фактори впливають на це? Передусім, це пізнавальний інтерес. Саме його втрата, як правило, є причиною зниження пізнавальної активності дітей.
Стимулами пізнавальної активності в навчально-виховному процесі, крім внутрішнього стимулу - пізнавального інтересу, також можуть виступати такі педагогічні прийоми, як заохочення, розкриття необхідності та значення навчального завдання (мотивація), підкреслення розвитку позитивних рис особистості в процесі навчання, своєчасне визнання успіхів учнів, активна позиція вчителя, довіра учням та інших, які вже стають зовнішніми стимулами пізнавальної активності учнів. Пізнавальна активність учнів є показником якості їх навчально-пізнавальної діяльності, спрямованості учня на ефективне опанування знань та способів діяльності.
У залежності від наведених вище критеріїв науковцями виділялись різні рівні пізнавальної активності учнів. У своїх дослідженнях О.С. Дубинчук встановила такі рівні пізнавальної активності [17]:
1. Репродуктивно-повторювальна активність, за допомогою якої досвід діяльності однієї людини накопичується завдяки досвіду іншої.
2. Пошуково-виконавча активність, яка передбачає такий ступінь самостійності учнів, яка дозволяє зрозуміти задачу та відшукати засоби її розв'язання без сторонньої допомоги.
3. Творча активність, яка дозволяє учню самостійно ставити певну задачу та вибирати нешаблонні, оригінальні шляхи її розв'язання.
Автор підкреслює, що ці рівні не ізольовані, а взаємопов'язані. Вони можуть співіснувати, відповідаючи шкільному віку. Ці ж рівні пізнавальної активності простежувались нами у процесі експериментальних досліджень при розв’язуванні математичних задач фінансового змісту на уроках математики в основній школі.
У відміченій системі рівнів пізнавальної активності звертається увага на те, що одним із головних завдань у педагогічній діяльності вчителя є збільшення активності учнів до рівня самостійності. Самостійність – це здатність з власної точки зору підійти до розв‘язання складних учбових питань, вміння виконувати цю роботу без сторонньої допомоги. Вона проявляється в їх критичній думці, в умінні висловити свої думки незалежно від чужого погляду. Активність не завжди поєднується із самостійністю, але є її необхідною умовою. Основою для самостійності виступає система знань, вмінь та навичок, якою володіє учень, а також використання вже засвоєного матеріалу приводить до опанування новими знаннями, вміннями та навичками. Так як самостійність завжди передбачає активність, то саме вона відображає ставлення учнів до учбово-пізнавальної діяльності.
В учбовому процесі повна самостійність учнів не є можливою. Тому головною ознакою самостійності учнів є досягнення поставленої мети без сторонньої допомоги, але з участю викладача в цьому процесі. Саме викладач найчастіше виконує такі функції діяльності як постановка її мети, формулювання завдання та перевірка отриманих результатів.
Є.Я. Голант [13] виділяє три види самостійності учнів:
· організаційно-технічна самостійність;
· самостійність в практичній діяльності;
· самостійність у пізнавальній діяльності.
Під пізнавальною самостійністю розуміють таку якість особистості, яка характеризується її прагненнями та вміннями без сторонньої допомоги отримувати знання, опанувати засобами діяльності та розв‘язувати пізнавальні задачі. “Говорячи про пізнавальну самостійність, - говорить М.І. Махмутов, - маємо на увазі вміння та здібності учнів самостійно виділяти основні та другорядні ознаки предметів, явищ та процесів матеріального світу, розкривати сутність нових понять шляхом абстрагування та узагальнення [39, c.18]”. Він виділяє такі ознаки пізнавальної самостійності учнів:
· вміння учнів отримувати нові знання та навички, використовуючи різні джерела;
· вміння в своїй подальшій освіті використовувати отримані раніш знання;
· вміння практично застосовувати знання, вміння та навички при вирішенні будь-якого життєво важливого питання.
Розвиток пізнавальної самостійності учнів у навчально-виховному процесі відбувається завдяки системі прийомів, методів, форм навчання, які адекватні досягнутому рівню навченості учнів. Їх вдалий підбір в методиці навчання приводять до активізації навчального процесу.
Наведені вище міркування дають можливість виділити такі критерії активізації пізнавальної діяльності учнів:
· формування пізнавального інтересу до об’єкта навчання;
· збільшення активності в процесі навчання;
· наявність ознак пізнавальної активності;
· прояв самостійності в навчально-виховній діяльності;
· розвиток пізнавальної самостійності.
Активізація пізнавальної діяльності учнів – це перехід до більш високого рівня активності та самостійності учнів у процесі навчання, який стимулюється розвитком пізнавального інтересу, та відбувається завдяки удосконаленню методів та прийомів навчального процесу.
Активізація пізнавальної діяльності учнів під час вивчення математики є однією з проблем сучасної шкільної освіти. Це пов'язане, в першу чергу, із зниженням інтересу молоді до навчання в цілому, а також з підвищенням ролі математики в різних галузях суспільства. Введення математичних задач фінансового змісту в курс математики основної школи виступає вагомим чинником активізації пізнавальної діяльності учнів, оскільки він впливає, в першу чергу, на формування пізнавального інтересу учнів до значення математики в сьогоднішніх умовах ринкових відносин у нашій країні.
Для активізації пізнавальної діяльності учнів також важливим є вдалий вибір методів, прийомів та засобів навчання, при якому враховуються певні психологічні особливості учнів. Головне призначення методів та прийомів навчання полягає в організації пізнавальної діяльності учнів.
Кожний метод навчання має зовнішню та внутрішню сторони. До зовнішньої сторони відносять різні способи його прояву у діяльності вчителя та учнів. Внутрішня сторона методу не підлягає зовнішньому спостереженню. Вона визначається змістом навчання, рівнем та характером діяльності [34].
Методи та прийоми навчання виконують такі функції:
· спонукальну (активізуючу), бо саме завдяки вдалому вибору методів розвивається інтерес учнів до навчання;
· освітню, бо в процесі їх використання учні набувають знання, вміння та навички;
· розвиваючу, бо система методів навчання націлена на формування та розвиток інтелекту, логічного мислення, пізнавальної активності та самостійності учнів.
Сьогодні, коли кожний учень розглядається як особистість, велика увага звертається на розвиваючу та активізуючу функції методів навчання.
У педагогіці існують різні класифікації методів та прийомів навчання: за джерелами здобуття знань (словесні, наочні, практичні), за характером пізнавальної діяльності (пояснювально-ілюстративні, репродуктивні, частково-пошукові, дослідницькі, проблемні), за способом організації навчально-пізнавальної діяльності (набуття нових знань, формування вмінь та навичок, застосування знань на практиці, перевірки й оцінювання знань та вмінь) тощо
Методи навчання є системним об’єктом. Він включає “прийоми та види навчальної діяльності педагога та пізнавальної діяльності вихованців у їх взаємозв’язку, дії та операції, які забезпечують досягнення поставлених завдань [40, с.72]”. Правильний вибір методів навчання у відповідності до цілей та змісту навчання і вікових особливостей учнів сприяє розвитку пізнавальної активності та пізнавальної самостійності учнів, а також підвищує інтерес учнів до предмету, виробляє вміння та навички використовувати набуті знання на практиці, спонукає учнів до самостійної діяльності, формує світогляд. Важливим зауваженням при виборі методу є той нюанс, що “ефективність застосування того або іншого методу залежить не лише від елементів пізнання, які необхідно засвоїти в процесі навчання, але й від того, скільки нових понять вводиться та скільки використовується опорних [17,c.36]”.
Г.І. Щукіна зазначає, що ізольовані методи та прийоми навчання не забезпечують продуктивної навчальної діяльності [65]. Це важливо пам’ятати, бо використання системи методів та прийомів веде до досягнення головних завдань процесу навчання. При цьому вони продовжують, доповнюють та розвивають один одного. Їх використання передбачає організацію взаємопов’язаної діяльності вчителя та учнів. Саме вчителю тут належить керівна роль.
Сьогодні в основі процесу навчання покладена мета створення умов для розвитку особистості. Тому вибір системи методів та прийомів навчання на цих засадах робить його розвиваючим та особистісно-орієнтованим.
Під розвиваючим навчанням в педагогіці розуміють спрямованість принципів, методів та прийомів навчання на досягнення найбільшої ефективності розвитку пізнавальних можливостей школярів [14]. Розвиваюче навчання націлене на формування розумових здібностей школярів, їх самостійності, інтересу до навчання, а також на вдосконалення різних форм сприйняття навчального матеріалу. Такий підхід до процесу навчання передбачає використання методів та прийомів, в основі вибору яких лежить ідея орієнтування не на досягнутий рівень розвитку учня, а на “зону ближнього розвитку”. Це означає, що завдання, які ставляться перед учнями дещо перевищують їх можливості, але виконання яких можливе завдяки певній допомозі вчителя. Таким чином, націлений навчальний процес сприяє розвитку пізнавальної діяльності учнів та активізує її.
Одним із типів розвиваючого навчання є проблемне навчання. Дуже тонко пов‘язує поняття проблемного та розвиваючого навчання М.І. Махмутов. “Розвиваючим навчанням, тобто яке веде до загального та спеціального розвитку, можна вважати тільки таке навчання, при якому вчитель, спираючись на знання закономірностей розвитку мислення, спеціальними педагогічними засобами приводить цілеспрямовану роботу по формуванню розумових здібностей та пізнавальних потреб своїх учнів в процесі вивчення основ наук. Таке навчання є проблемним [39, с.16]”.
Суть проблемного навчання полягає у пошуковій діяльності учнів, яка починається з постановки питань, розв’язування проблем і завдань у проблемному викладі й поясненні навчального матеріалу та різноманітних самостійних форм роботи.
Проблемні методи навчання є ефективними засобами активізації пізнавальної діяльності учнів. Вони сприяють інтелектуальному розвитку учнів і водночас формують світогляд, моральні та емоційні риси особистості. Проблемно-пошукове навчання зближує процес навчання в школі з науковим пізнанням, розвиває творче мислення.
Досягнення найвищого рівня емоційного стану, прояву пізнавальної активності та самостійності є прагненням активізації пізнавальної діяльності учнів за допомогою використання проблемного навчання. Для цього діяльність вчителя та учнів складається з певних кроків, які використовуються в роботі з будь-якими проблемними ситуаціями (див. табл. 1.1).
Таблиця 1.1
Чотири рівні проблемності в навчальному процесі [54]
|
Діяльність вчителя |
Діяльність учнів |
|
| 1рівень | активізує та контролює знання; ставить та формулює навчальну задачу; розв‘язує проблему; закріплює знання учнів, організовує самостійну роботу. | розуміють необхідність актуалізації знань; розуміють суть проблемної ситуації; осмислюють хід її розв‘язання; виконують вправи за зразком та тренувальні вправи в процесі виконання самостійної роботи. |
| 2 рівень | керує підготовчою роботою; актуалізує опорні знання; діагностує можливості учнів до розв‘язання навчальної проблеми; створює проблемну ситуацію; формулює проблему; направляє учнів на розв‘язання проблеми; організовує самостійну роботу | розуміють необхідність актуалізації знань та створеної проблемної ситуації; разом з вчителем розв‘язують проблему; виконують вправи на перевірку та закріплення розв’язаної проблеми; тренуються у виробленні навичок. |
| 3 рівень | керує підготовчою роботою; актуалізує опорні знання та створює проблемну ситуацію; керує розв‘язанням навчальної проблеми; організовує самостійну роботу | осмислюють актуалізовані знання та створену проблемну ситуацію; формулюють навчальну проблему; висувають гіпотезу та дедуктивно її обґрунтовують; перевіряють розв‘язання; виконують самостійну роботу |
| 4 рівень | керує підготовчою роботою; ставить завдання; організовує, керує навчальним процесом; організовує самостійну роботу | усвідомлюють необхідність самостійного засвоєння нових знань; формулюють навчальну проблему; висувають гіпотезу; обґрунтовують її дедуктивно; перевіряють правильність доведення; творчо застосовують здобуті знання на практиці |
Проблемний підхід є засобом розвитку творчого мислення школярів. Як зазначають сучасні педагоги [42], виходячи з індивідуальних особливостей учнів, темпу опанування ними учбового матеріалу, проблеми перед учнями слід ставити доступі, посильні, цікаві, природні; у процесі викладення матеріалу на уроці пов’язувати нове з вже відомим, постійну увагу приділяти спостереженню, експерименту, узагальненню та створенню атмосфери творчого пошуку. Завдяки цьому відбувається розвиток пізнавальної активності та пізнавальної самостійності учнів, що приводить до активізації їх пізнавальної діяльності.
На сьогоднішньому етапі розвитку освіти виникає потреба розв’язання проблеми пошуку та розкриття внутрішніх резервів розвитку особистості учня. Тому в основу навчально-виховного процесу починають закладати пріоритет індивідуальності й самооцінки дитини, її унікальності та її власного досвіду. Таке навчання отримало назву особистісно-орієнтоване.
Особистісно-орієнтоване навчання – це організація навчання на засадах глибокої поваги до особистості вихованця, врахування особливостей індивідуального розвитку, ставлення до нього як до свідомого відповідального суб’єкта навчально-виховної взаємодії. Воно передбачає формування цілісної особистості, яка усвідомлює власну гідність та поважає інших людей [42]. Завдяки такому підходу учень стає активним суб’єктом процесу навчання, а метою діяльності педагога є віднайти, підтримати та розвити індивідуальні можливості й здібності дитини, закласти в нього основи самовиховання. само розвитку, самореалізації, самовдосконалення. Самовдосконалююча особистість – це головна мета особистісно-орієнтованого підходу. Для її досягнення підбираються та організуються зміст навчання, його методи форми та прийоми таким чином, щоб учень мав можливість проявити вибірковість у відношенні до завдань та предметів навчання. Як зазначається І.С. Якиманською [67], впровадження особистісно-орієнтованого навчання в шкільну практику можна здійснити через диференціацію та індивідуалізацію навчання. Ці елементи педагогічної діяльності мають великий вплив на активізацію пізнавальної діяльності учнів.
Індивідуалізація навчання засобами диференціації потребує врахування не лише якості засвоєння навчального матеріалу, а й формування активної навчальної діяльності учня. Інколи поняття “диференціація” та “індивідуалізація” в педагогічній літературі ототожнюються. Врахування засад особистісно орієнтованого та розвиваючого навчання вимагає розгляду цих понять не лише з позиції вчителя, а й з точки зору учня в цьому процесі. Це дає підстави звернути увагу на уточнення цих понять.
Індивідуалізація – це організація навчально-виховного процесу, за якої важливим є врахування індивідуальних особливостей кожного учня, перспектив його подальшого розумового розвитку, гармонійного вдосконалення особистості. Така організація навчання сприяє формуванню пізнавального інтересу учнів, їх активності та самостійності, розвиває творчі здібності особистості.
Під диференціацією навчання розуміють спеціально організована пізнавальна діяльність, яка здійснюється з врахуванням індивідуальних особливостей учнів та спрямована на їх інтелектуальний розвиток. Для впровадження цього напрямку в педагогіку важливим елементом стає добір форм, методів та прийомів навчальної діяльності відповідно до типологічних особливостей учнів. Саме різний підхід вчителя до груп учнів, які виділені з врахуванням індивідуальних особливостей, полягає в основі організації диференційованого навчання. Диференційоване навчання створює сприятливі умови для того, щоб учень міг розкрити та проявити властиві йому індивідуальні особливості. Таким чином, диференціація навчання полягає у формуванні навчальних груп за певними ознаками і проведення відповідно до цього навчальної роботи з врахуванням індивідуальних особливостей учнів. Це забезпечує оптимальні результати розвитку особистості учня. Диференціація стає засобом індивідуального навчання.
Ідеї розвиваючого та особистісно – орієнтованого навчання націлені на активізацію пізнавальної діяльності учнів. В процесі такого навчання розвитку розумової активності та пізнавальної самостійності мають бути підпорядковані всі методи, прийоми та форми навчально-виховного процесу. Важливим в їх виборі є врахування вікових та психологічних особливостей учнів. Це націлює сучасну педагогічну науку на пошук нових елементів навчання, які б сприяли активізації пізнавальної діяльності учнів та підвищували їх інтерес до навчальної діяльності.
Математичні задачі фінансового змісту виступають засобом активізації пізнавальної діяльності учнів у процесі вивчення математики. Дослідження підходів, методів та прийомів роботи з такими задачами є наступним кроком дослідження.
1.2. Математичні задачі фінансового змісту як засіб активізації пізнавальної діяльності учнів
Історія свідчить, що математика як наука виникла з задач. Її розвиток полягає, в основному, у розв’язуванні задач. В математичній науці задачі – це і джерело, і мета її розвитку.
У навчанні математики задачі теж виступають як ціллю, так і засобом. Їх розв‘язування сприяє вихованню учнів, особливо вихованню волі, спостережливості та інших якостей. Під час розв’язування текстових задач також вирішується проблема розвитку логічного мислення учнів. Завдяки такій роботі в учнів формуються прийоми мислення - аналіз, синтез, абстрагування тощо. Особливо корисні задачі для активізації мислення учнів, для виявлення творчих здібностей та їх розвитку. “Використання задач, - зазначає Е.Ф.Вінокуров, - перетворює навчання на творчий процес та сприяє глибокому осмисленню й усвідомленню матеріалу [10, с.24]”.
Роль та місце задач у навчанні математики історично змінювались. Задача була метою навчання, тобто математику вивчали саме для того, щоб засвоїти правила розв‘язання типових задач. При цьому використовувались задачі суто прикладного характеру, які переслідували прикладні цілі.
Зі зміною цілей навчання, що обумовлювалось розвитком суспільства, змінюється і роль задач у навчальному процесі. С.І. Шорох-Троцький (1915 р.) зазначав, що “арифметичні задачі при розумному навчанні повинні були не метою, а лише засобом навчання арифметики [64,c.73]”.
Сьогодні роль задач в процесі вивчення математики визначається, з одного боку, зведенням кінцевих цілей цього навчання до оволодіння учнями методами розв‘язання системи задач. З іншого боку, вона визначається досягненням кінцевої цілі навчання – формування всебічно розвиненої особистості, що можливе за допомогою розв‘язання учнями вдало сформованої навчальної системи задач.
Що ж таке “задача”? В педагогічній, психологічній та методичній літературі зустрічається багато спроб дати визначення цьому поняттю. Різні підходи умовно можна поділити на дві групи в залежності від відношень між суб‘єктом та задачею. До першої групи відносяться означення поняття “задача” як ситуації зовнішньої діяльності, яка може бути проаналізована та описана окремо від суб‘єкта, який здійснює розв‘язування задачі (А.В. Брушлинський [7], М.А. Данілов [16], А.М. Матюшкін [38] та ін.).
До другої групи відносяться визначення поняття “задача”, які включають психологічний зміст та зводяться до загальної характеристики задачі як мети, яка дана в певних умовах, та як особливої характеристики діяльності суб‘єкта. Тут задача розглядається як суб‘єктивне відображення такої зовнішньої ситуації, в якій розкривається цілеспрямована діяльність суб‘єкта (Л.П. Гурова [15], Ю.М. Колягін [30; 31], Я.А. Пономарьов [45] та ін.).
З метою вивчення внутрішніх елементів задач (наприклад, її типу, структури) розглядається перше визначення. Якщо досліджують психологічний характер діяльності суб‘єкта - то вибирається друге визначення.
Робота над задачею дає можливість досягти не лише однієї поставленої мети, а одночасно виконати декілька учбових завдань. Це можливо завдяки виконанню різних навчальних функцій математичними задачами. Це і дидактичні, і пізнавальні, і розвиваючі функції.
Велике поширення отримав розподіл задач на три види: задачі на обчислення, на побудову та на доведення. Такі назви можна побачити навіть у шкільній програмі з математики. Існує також розподіл задач на стандартні та нестандартні.
В будь-якому розподілі знаходиться місце для математичних задач фінансового змісту. Хоча цей клас задач виділяється дуже умовно. В різних класифікаціях задачі такого типу рівномірно розповсюджуються майже за всіма пунктами класифікації.
Під математичною задачею фінансового змісту (фінансово-математична задача) ми розуміємо задачу, фабула якої розкриває використання математики в фінансових дисциплінах, ознайомлює із застосуванням математичних понять, операцій та законів у фінансовій сфері. Таке означення показує, що ці задачі можуть використовуватися протягом всього учбового процесу.
Останнім часом посилився пошук шляхів активізації пізнавальної діяльності учнів у процесі навчання математики за допомогою задач. Введення математичних задач фінансового змісту в шкільний курс ґрунтується на засадах та принципах процесу активізації пізнавальної діяльності учнів.
Математичні задачі фінансового змісту виконують:
· освітню функцію, бо їх використання спрямоване на формування у школярів системи знань, вмінь та навичок на різних етапах навчання;
· розвиваючу функцію, бо робота з ними розвиває вміння осмислювати зміст понять, застосувати здобуті знання на практиці, аналізувати результати, робити відповідні узагальнення, порівняння та висновки;
· виховну функцію, бо економічне та фінансове виховання на уроках математики може здійснюватися насамперед завдяки цьому класу задач;
· контролюючу функцію як навчальні задачі.
Кожна математична задача фінансового змісту, яка пропонується учням для розгляду, повинна відповідати наведеним вище вимогам. До математичних задач фінансового змісту висуваються ще й додаткові вимоги, які важливі для навчальних задач як практичного, так і прикладного змісту [60]:
· пізнавальна цінність задачі та її виховний вплив на учнів;
· доступність для школярів використаного в задачі нематематичного матеріалу;
· реальність описаної в умові задачі ситуації, числових даних, постановки питання та отриманого результату.
При формулюванні умов математичних задач фінансового змісту бажано ставити питання задачі таким чином, щоб для відповіді або для розв‘язання можна було застосовувати характерні властивості використаних фінансових понять та різні фінансові відношення між ними. Крім того, необхідно здійснювати роз‘яснення фінансових термінів або вводити їх в задачу таким чином, щоб їх зміст був зрозумілим із тексту задачі.
Для досягнення поставленої навчальної мети, а також для активізації діяльності учнів можуть бути запропоновані різні методи роботи з фінансово-математичними даними в задачах.
Схемою в цьому випадку може стати структура діяльності для розв‘язування задачі, запропонована Л.М. Фрідманом [57], в якій він виділяє чотири етапи:
1. Аналіз змісту задачі.
2. Пошук плану розв‘язання.
3. Реалізація знайденого плану розв‘язання та доведення, коли отриманий результат задовольняє вимогам задачі.
4. Обговорення (аналіз) проведеного розв‘язування.
Робота над будь-якою задачею будується за таким алгоритмом. Звернемо увагу на те, що першим і невід‘ємним кроком є момент залучення учня до розв‘язування задачі.
Розв‘язання будь-якої задачі починається з ознайомлення з її змістом, який може зацікавити чи не зацікавити учнів.
Інтерес, який виникає до змісту задачі, не лише сприяє адекватному осмисленню її вимог, але й надає цій вимозі особистого характеру. Це спрямовує діяльність учня на розв‘язування конкретної задачі – отримання результату. Розв‘язування багатьох задач потребує від людини добре розвинених здібностей до творчої діяльності або, принаймні, здібностей та вмінь відшукати оптимальне в даних умовах розв‘язування. Багатьох учнів приваблює не так сама задача, як процес щодо її розв‘язання. Розв‘язування математичних задач фінансового змісту може бути організовано по-різному: в формі змагання на кращого “банкіра”, “фінансиста”; у вигляді пошуку помилок, придумування контрприкладів… Учні із задоволенням беруть участь у змаганнях щодо розв‘язування задач, бачать продуктивність сумісного розв‘язання проблеми, обговорюють розв‘язки та відповіді друзів.
Навчання – це процес, який залежить від загального розвитку дитини та від особливостей психологічних процесів. Будь-яке новоутворення формується у співпраці вчителя та учня.
Поступове ускладнення завдань, постановка проблем, розв‘язування задач на порівняння, узагальнення та класифікацію при використанні фронтальної роботи веде до формування вмінь розв‘язувати задачі, до постановки та вирішення проблем, до формування прийомів розумової діяльності. В результаті фронтальна робота поступається місцем розгорнутим відповідям окремих учнів та самостійній роботі кожного.
Робота з математичними задачами фінансового змісту вимагає ширшої схеми діяльності та ґрунтується на засадах математичного моделювання. Для активізації пізнавальної діяльності учнів при роботі з математичними задачами фінансового змісту організація навчальної діяльності повинна бути побудована за наступною схемою:
1. Актуалізація раніше усвідомлених знань, вмінь та навичок.
2. Вивчення задачі і здійснення її структурного аналізу:
· виділення об’єктів задачі та відношень між ними;
· виділення величин, які розглядаються в даній задачі;
· пригадування і встановлення співвідношень між величинами.
3. Тлумачення фінансових термінів, які використовуються в задачі, та знаходження математичних зв’язків між ними.
4. Побудова математичної моделі: складання числових виразів, рівнянь, нерівностей, використання відомих співвідношень, формул, тотожностей тощо.
5. Розв‘язання задачі в середині побудованої моделі, що включає:
· дискусію щодо закладеної в задачу проблеми та висування деяких пропозицій щодо її розв’язання;
· розробку плану розв‘язання задачі;
· вибір відомостей, які необхідні для розв‘язання;
· деталізацію плану розв‘язання;
· підведення підсумків розв‘язання та отримання остаточного результату;
· перевірку отриманих фактів.
6. Аналіз отриманого розв‘язку та пошук інших, можливо раціональніших, способів розв‘язання.
7. Перевірка правильності моделювання (складання числових виразів, рівнянь, нерівностей) та розв’язку задачі.
8. Знаходження аналогів даної проблеми в житті.
9. Встановлення меж застосування способу розв’язування задачі.
10. Розгляд можливих розширень та узагальнень проблеми.
11. Підведення підсумків виконаної роботи.
Практика роботи над задачами фінансово-математичної тематики, показала, що, для досягнення мети фінансового розвитку школярів та їх підготовки до життя в ринкових умовах також доцільно дотримуватись таких принципів:
1. Знайомство з головними економічними законами держави, а саме економічними положеннями Конституції України, основами оподаткування, фінансово-розрахунковими операціями тощо, повинно бути адаптоване до різних вікових груп.
2. На уроках математики мають використовуватись документи фінансової діяльності держави та відомих підприємств.
3. Під час розв’язування задач із фінансовою фабулою, слід використовувати відповідну методику, яка дозволяє ефективно обчислити відповідь суто математичної задачі з поясненням фінансових термінів, які зустрічаються в тексті задачі.
4. Виявляти фінансову залежність між фінансовими величинами, які відповідають реаліям сьогодення.
5. Використовувати відповідний набір задач для розвитку та формування таких рис характеру, як бережливість, економність. Для розвитку пізнавально-оцінюючих рис характеру використовувати різні методичні прийоми та засоби.
Для реалізації сформульованих принципів фінансової освіти та виховання школярів на уроках математики є необхідним уточнення фінансових аспектів, які можуть бути розглянуті на уроках при роботі з фінансово-математичними задачами. Ставлячи за мету збільшення фінансових знань учнів під час розв‘язання задач, також потрібно звернути увагу на розвиток навичок аналізувати причинно-наслідкові зв‘язки між фінансовими факторами та їх математичною інтерпретацією. Завдяки цьому виникає потреба в збільшенні розгляду фінансових понять, задач та проблем, що несуть в собі як математичний, так і фінансово-економічний зміст. Все це можливо здійснити за допомогою шкільного курсу математики.Економічний розвиток деяких країн показує, що фінансово-економічна обізнаність у країні є головним джерелом фінансового розвитку держави. Не випадково в розвинутих країнах цьому поділяється велика увага: з фінансовими проблемами учні знайомляться вже з перших шкільних років та протягом всього навчального періоду поповнюють навичками розв‘язання фінансово-математичних задач. Сьогодні, коли умови ринкових відносин у державі набувають все більших обертів, доцільно адаптувати учнів до розв’язування низки фінансових проблем реального життя.
Бюджет кожної сім'ї є важливою складовою фінансової системи держави. Серед багатьох аспектів проблеми підготовки учнів до дорослого життя важливим є формування в учнів уявлення про сімейний бюджет та його особливості. Адже розумне планування власних доходів та витрат дозволяє родині заощаджувати кошти та спрямовувати їх на підвищення добробуту. Гарним засобом формування таких уявлень є математичні задачі на сімейний бюджет, які можна і потрібно пропонувати учням під час навчання математики. Вони охоплюють велике коло фінансових операцій, мають прикладну спрямованість.
Для розумного використання власних коштів доцільно знати особливості роботи банків із клієнтами. Використання депозитних рахунків для заощаджень населення, можливість отримання кредитів для споживчих цілей або розвитку власного бізнесу, забезпечення безготівкового обігу грошей є стабілізуючим фактором забезпечення фінансової стабільності держави.
Ринкові відносини в державі розширюються та міцніють, а робота з цінними паперами поволі стає невід’ємною складовою фінансової діяльності кожного громадянина. Такий стан в суспільстві вимагає від молодих людей, які тільки починають самостійне життя, мати певний набір практичних знань з фінансової науки, яка базується на знаннях із математики.
Податкова політика держави визначає спроможність її економіки вийти на рівень стабільного та стійкого розвитку. Ознайомлення учнів з системою обчислення податків та їх використання державою є важливим елементом загальної підготовки майбутнього громадянина України для життя в умовах ринкової економіки. Сплачуючи податки, громадянин одержує певні послуги від держави.
Разом із розвитком ринкових відносин зростає ймовірність виникнення непередбачуваних ускладнень, підвищується ступінь ризику на всіх рівнях. Це обумовлює необхідність захисту громадян від можливих втрат. Саме страхова діяльність у державі зосереджується на розв’язанні таких проблем. Страхування в ринкових відносинах ґрунтується на попередньому створенні страхових фондів зі страхових внесків та на відшкодуванні збитків потерпілим. Тут розрахунок збитків, їх компенсація відбуваються у грошовій формі, і таким чином, відбувається тісний зв’язок із фінансовим розвитком країни.
Отже, фінансові знання кожного громадянина мають велике значення в розвитку економіки нашої держави.
Використовуючи фінансові дані у математичних задачах фінансового змісту можна поступово знайомити учнів із фінансовим станом країни, з проблемами держави та шляхами розв‘язання проблем власного характеру. Таким чином, основні задачі, які можуть використовуватися в процесі вивчення математики в середній загальноосвітній школі, можуть бути розподілені за мал. 1.1.
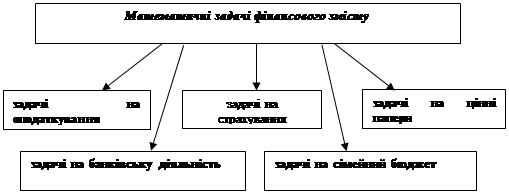
Мал. 1.1 Математичні задачі фінансового змісту в курсі математики основної школи
Введення задач на банківську діяльність до курсу математики основної школи, які пов‘язані з депозитними вкладами та наданням кредитів, ознайомлює учнів з фінансовими величинами які використовуються в діяльності банків та показує математичну залежність між ними. Такі прикладні задачі розширюють знання учнів про банківську систему України та розкривають її особливості.
Ознайомлення учнів з системою обчислення податків через математичні задачі на оподаткування та використання податкових надходжень державою є важливим елементом загальної підготовки майбутнього громадянина України для життя в умовах ринкової економіки. На уроках математики, працюючи з податковими даними, учні усвідомлюють необхідність сплати податків, систему їх нарахування та подальше використання податкових надходжень державою.
Через математичні задачі на цінні папери можливе ознайомлення учнів основної школи з ринком цінних паперів, що є необхідним елементом сьогоднішньої освіти в Україні. Використання в процесі навчання математичних задач на цінні папери розширює клас прикладних задач, надає більше можливостей для розвитку творчості дитини та ілюстрації математичних законів на життєвих реальних об’єктах, які займають важливе місце в суспільстві в умовах ринкової економіки.
Розумне планування власних доходів та витрат може бути проілюстровано за допомогою математичних задач на сімейний бюджет, що дозволяє привчати учнів основної школи заощаджувати власні кошти та спрямовувати їх на підвищення власного добробуту. Важливо серед багатьох аспектів проблеми формування підготовки учнів до дорослого життя розуміння сімейного бюджету, що можливо досягнути за допомогою учбових математичних задач. Наведемо приклад такої задачі, що використовувалась у девятому класі при повторенні теми "Лінійна функція".
Задача 4. Нехай х – всі доходи родини за місяць, а витрати в середньому становлять 700 гривень на місяць. Скласти функцію прибутку родини: а) за місяць; б) за рік.
Особливості роботи з задачами на страхування в курсі математики основної школи полягають в тому, що в ході їх розв’язування відбувається тлумачення різних страхових термінів, показується математична залежність між ними. Учні вчаться застосовувати набуті математичні знання в звичайних страхових ситуаціях, які відбуваються в повсякденному житті. Для прикладу відмітимо задачу, яка була використана в ході експерименту у дев’ятому класі при вивченні теми "Числові послідовності":
Задача 5. Для залучення клієнтів страхова компанія використовує активну політику щодо зменшення страхового тарифу в залежності від кількості об’єктів страхування. Клієнт вирішив застрахувати відразу 5 об’єктів, вартість кожного 20 000 грн. Яка сума страхових внесків, якщо страховий тариф при страхуванні одного об’єкта 3 %, та він зменшується при страхуванні кожного наступного об’єкту на 0,5% ?
Розв‘язуючи математичні задачі фінансового змісту, учні вчаться застосовувати математичні знання в фінансовій сфері, що сприяє розвитку особистості та готує їх до дорослого життя в умовах ринкової економіки. Через математичні задачі фінансового змісту відбувається поступове ознайомлення учнів з фінансовими термінами, поняттями та означеннями протягом курсу математики в основній школі (дод1.3. Психолого-методичні основи активізації пізнавальної діяльності учнів основної школи під час навчання математики
Активізація пізнавальної діяльності учнів залежить від багатьох факторів, які можна поділити на дві групі. Першу групу складають суб’єктивні фактори, до яких відносяться вікові та індивідуальні особливості учнів, які проявляються у їх здібностях, рівнях пізнавальної діяльності, мотивах навчання тощо. До другої групи відносяться об’єктивні фактори: зміст навчання, методи та прийоми навчально-педагогічної діяльності вчителя, способи керування навчальною діяльністю учнів. Ці групи тісно пов’язані між собою, оскільки суб’єктивні фактори, формуючись під впливом об’єктивних, опосередковують вплив останніх на учня.
1.3 Психолого-методичні основи активізації пізнавальної діяльності учнів основної школи під час навчання математики
1.3.1 Психологічні основи активізації пізнавальної діяльності учнів підліткового віку
Досягнення активізації пізнавальної діяльності відбувається за рахунок створення необхідних для цього умов - реалізації внутрішнього потенціалу та пізнавальних можливостей кожної дитини. “Пізнавальні процеси є складовою будь-якої людської діяльності, які забезпечують ту або іншу її ефективність [54, c.47]”. Важливо допомогти дитині пізнати себе, свої здібності, нахили в процесі навчально-виховної діяльності.
У підлітковому віці психологи [7] виділяють три стадії:
· “локально-капризна”(10-11 років), коли загострена потреба у визнанні дорослими;
· “право-значима”(12-13 років), яка характеризується потребою в суспільному визнанні, в важливості власної діяльності;
· “стверджувально-дійова”(14-15 років), коли домінує готовність проявити себе, використати власні можливості.
Як відомо, на будь-якій стадії підліткового віку всі сторони розвитку включають перехід від дитинства до дорослості. Внаслідок цього відбувається перебудова організму, зміна відносин з однолітками та з батьками. Також змінюються моральні, етичні, соціальні та духовні потреби особистості, відбувається становлення самосвідомості. Найважливішим новоутворенням у підлітковому віці, на думку психолога Л.С.Виготського, є те, що “у драму розвитку вступає нова діюча особа, новий якісно своєрідний фактор – особистість самого підлітка [9,с.238]”. Тут виникає конфлікт між уявою про себе та власними реальними можливостями. У цьому віці спостерігається потреба зміцнювати свою соціальну роль, спостерігається допитлива думка, як він виглядає в очах інших, особливо це стосується небайдужих йому людей. Самосвідомість підлітка характеризується почуттям дорослості. Підліток вже починає ставити себе на місце дорослого та перестає вважати себе дитиною. Але для повної реалізації власних потреб не вистачає досвіту, розвитку моральних, інтелектуальних та фізичних якостей. На цьому базуються характерні вікові конфлікти підлітків з навколишніми людьми. Для розв’язування цієї проблеми психологи радять залучати дітей підліткового віку в діяльність, яка має серйозні мотиви, але посильна для даного віку [50].
У цьому віці прагнення до спілкування обумовлено потребою визнання цінності власної особистості та власного місця в колективі. Підліток знаходиться під впливом групи однолітків, його власний погляд залежать від колективної думки. Тому навчальна діяльність повинна включати якомога більше колективних форм організації.
Процес навчання стає реалізацією активності учня підліткового віку. В процесі власного вибору засобів та шляхів у процесі навчання, учні самостверджуються. Вони починають набувати систематичні знання з основ наук, переходять до теоретичних понять, що вимагає досконалих способів набувати знання. Розвиток наполегливості у розв’язанні проблем, умінь приймати рішення, здатності знаходити правильний шлях розв’язання стає основою навчальної діяльності цього віку. В основній школі формуються вміння доводити істинність набутих знань, тобто вміння логічно міркувати, поєднувати індукцію з дедукцією, усвідомлювати хід міркувань та самокритично ставитись до власних висновків.
У більшості підлітків відмічається зростання обсягу уваги, її концентрації і стійкості, розвивається цілеспрямоване запам’ятовування та зростає їх продуктивність. Мислення учнів цього віку відзначається критичністю, власні дії стають більш контрольовані.
У підлітковому віці зазнає якісних змін мотивація навчання, яка все більше пов’язується з підготовкою до майбутньої трудової діяльності, усвідомлюючи обов’язок. Завдяки цьому поглиблюються і диференціюються пізнавальні інтереси. Прагнення підлітків до індивідуалізації та ствердження власної позиції може підсилювати пізнавальні мотиви учнів. Це вимагає великої уваги з боку вчителя. Тому важливо підкреслити важливість використання принципів навчання, що ведуть до активізації пізнавальної діяльності підлітка: проблемність, діалог, індивідуальний підхід тощо. Однак у деяких підлітків спостерігається нестійкість мотивів та інтересів до навчання. Послаблення інтересу до навчання може виникнути внаслідок власних невдач в цьому процесі, які викликають внутрішні переживання, а самолюбство породжує прагнення зробити вигляд, ніби оцінки успіхів у навчанні не мають для них істотного значення. Це стає однією з причин негативного ставлення до навчання.
Наприкінці підліткового віку учні починають усвідомлювати необхідність самостійного вибору подальшої програми освіти та трудової діяльності. Вона ґрунтується на сформованості достатньо стійких інтересів та переконань, на орієнтованості в різних галузях праці та суспільно корисній діяльності.
Врахування зазначених психологічних особливостей розвитку підліткового віку приводить до вибору певних методів та прийомів навчальної діяльності, які сприяють активізації пізнавальної діяльності при роботі з математичними задачами.
У цьому віці відбувається спостереження, конкретизація, узагальнення та порівняльний аналіз фінансової ланки життя. Для допомоги дитині в усвідомленні фінансово-математичних істин повинен бути підручник, якій надалі стане довідником на все життя.
Врахування особливостей навчання допомагає підібрати відповідні методи навчання та учбовий матеріал, який усвідомлюють школярі на базі математичних задач фінансового змісту.
1.3.2 Методи, засоби та прийоми активізації пізнавальної діяльності учнів 9 класу у процесі розв’язування математичних задач фінансового змісту
Реформою математичної освіти передбачено в процесі навчання все більше використовувати різноманітні форми та методи організації учбового процесу. Це дозволяє враховувати відмінності в підготовці учнів, в рівнях їх пізнавальної активності, а також реалізовувати міжпредметні зв'язки та приділити більше уваги виховній роботі в процесі навчання.
Проблему розвитку пізнавальної активності та самостійності учнів не можна розглядати окремо від удосконалення форм, методів та засобів навчання. Це дає підставу для ретельного аналізу організації навчання та впливу методів, засобів та прийомів на активізацію пізнавальної діяльності учнів. Серед методів, засобів та прийомів навчання, що стимулюють активізацію пізнавальної діяльності учнів, дослідники виділяють такі:
· оновлення змісту і зміцнення міжпредметних зв’язків;
· удосконалення методів навчання;
· розробки та впровадження методів проблемно-розвиваючого навчання;
· модернізація уроку;
· розширення набору форм самостійної роботи та активізація самостійної роботи на уроці;
· запровадження особистісно-орієнтованого навчання;
· комп’ютеризація навчального процесу.
Розглянемо особливості наведених методів, прийомів та засобів при використанні їх в процесі розв’язування математичних задач фінансового змісту.
Відразу зауважимо, що введення математичних задач фінансового змісту в курс математики основної школи є елементом оновлення змісту і зміцнення міжпредметних зв’язків. Підставою для такого висновку є закладені фінансові данні цих задач, які розширюють знання, вміння та навички дітей у використанні математичних знань. Такі задачі раніше не використовувались в курсі математики основної школи, але сьогоднішні ринкові відносини в державі є підґрунтям для оновлення системи учбових задач саме завдяки включенню математичних задач фінансового змісту в процес навчання.
Для досягнення активізації пізнавальної діяльності учнів у процесі навчання всі педагоги звертають увагу на важливість використання різних методів та прийомів проблемного навчання. С.Л. Рубінштейн, характеризуючи природу розумового процесу, зазначав: “Початковим моментом розумового процесу як правило є проблемна ситуація. Мислити людина починає тоді, коли в неї з’являться потреба щось зрозуміти. Мислення починається з проблеми чи запитання, здивування чи нерозуміння, з протиріччя [50, с.26]”.
Проблемний підхід при вивчені курсу математики основної школи є орієнтованим на активізацію мислення та пізнавальної діяльності учнів. Навчання учнів за допомогою готових прийомів розумової діяльності дає можливість досягти учнями лише звичайної активності, але не творчої. Використання проблемних ситуацій при роботі з математичними задачами фінансового змісту підвищує продуктивність пізнавальних процесів, розвиває творчі здібності учнів, веде до глибокого та міцного засвоєння знань, вчить робити самостійні “відкриття” та знаходити їх застосування в бурхливому потоці життя.
Прояв активності та самостійності учня в проблемній ситуації можливий на різних рівнях активізації пізнавальної діяльності, а саме:
1. Вивчення та розв‘язання проблеми за вимогою вчителя.
2. Вивчення та розв‘язання проблеми, завдяки виникненню здивування, бажання подолати протиріччя, які виникають.
3. Вивчення та розв‘язання проблеми, яка зацікавлює та потребує уважної роботи.
4. Пізнавальний інтерес до роботи з проблемою.
Протиріччя, які виникають на певних етапах роботи з математичними задачами, служать джерелами проблемних ситуацій в процесі вивчення математики. З цього приводу, учбові проблемні ситуації поділяються на [60]:
· пов‘язані з перекладом реальних задач на мову математики;
· пов‘язані з математичним формулюванням задач;
· пов‘язані з перекладом математичного результату на мову, на якій була сформульована задача.
З усіма відміченими проблемами учень зустрічається при роботі з математичними задачами фінансового змісту. Тому робота з такими задачами може бути побудована на елементах проблемного підходу. Наприклад, робота над задачею у дев’ятому класі при повторенні теми “Функції” може бути проведена так.
Задача. Заповнити таблицю 1.2 та побудувати графіки податкових надходжень зведеного бюджету з кожного виду податків.
Запитання: Чи достатньо даних наведених в таблиці для виконання завдання?
Відповідь: Так, але для більшої точності графіків потрібно заповнити порожні місця в таблиці.
Таблиця 1.2
Структура податкових надходжень зведеного бюджету, %
| Рік | Податкові надходження | Прибутковий податок з громадян | Податок на прибуток підприємств | Податок на додану вартість | Акцизний збір | Інші податки |
| 1995 | 100 | 12,3 | 37,7 | 35,1 | 3,2 | 11,7 |
| 1996 | 100 | ? | 32 | 36,4 | 3,7 | 12,8 |
| 1997 | 100 | 15,3 | 26,5 | ? | 5,4 | 17,4 |
| 1998 | 100 | 16,3 | ? | 31,4 | 5,4 | 21,6 |
| 1999 | 100 | 17,8 | 24,6 | 33,8 | ? | 16,7 |
| 2000 | 100 | ? | 24,4 | 34,5 | 7,1 | 17,1 |
Запитання: Який основний принцип покладено в систему податкових надходжень, що описані в таблиці?
Відповідь: Загальна кількість податкових надходжень за рік повинна становити 100 %.
Запитання: За допомогою яких математичних дій та операцій можливе відшукання даних, яких не вистачає в таблиці?
Відповідь: Для цього потрібно, щоб сума чисел, які записані в рядку, дорівнювала 100. Тому використовується додавання та віднімання величин.
Учні самостійно заповнюють порожні клітинки таблиці.
Запитання: Яку залежність між заданими величинами треба використати, щоб отримати функціональну залежність?
Відповідь: Величина будь-якого виду податку залежить від року, в якому вона була отримана. Тому рік – незалежна величина, а кількість відсотків, що припадає на даний вид податку, – величина залежна.
Запитання: Яким чином можливе відображення цієї залежності на графіку?
Відповідь: За х позначаємо рік, в якому обчислювався податок, а за у – величину відсотків даного виду податку. Відобразимо наведені данні на координатній площині у вигляді точок з координатами (х, у), після чого з’єднуємо отримані точки плавною лінією.
Учні діляться на 5 груп, і кожна група будує відповідний графік.
Після виконання завдання обов’язково треба провести аналіз отриманих даних, а також поставити додаткове завдання - спробувати знайти математичну функцію, яка має схожий графік.
Подальша робота полягає в: аналізі отриманих графіків як з математичної точки зору, так і з фінансової; знаходженні зв’язку математичних властивостей отриманих графіків з фінансовими величинами.
Використання задач з не сформульованим запитанням, з недостачею даних, з зайвими даними, з декількома розв‘язками, задач на доведення, на логічне міркування приводить до створення проблемної ситуації в навчанні. Завдяки таким задачам, які ставлять учнів у ситуації, характерні для життєвої практики, відбувається актуалізація досвіду, який мають учні, та знань фінансових операцій. Працюючи з математичними задачами фінансового змісту, вчитель має надавати додаткову інформацію учням щодо тексту задачі або її відповіді.
Практика роботи з математичними задачами фінансового змісту показує, що проблемна ситуація в процесі їх розв’язування виникає, коли:
· завдання містить в собі термінологію, яка не розглядалась раніше та не було виведено зв‘язку з іншими фінансово-математичними операціями;
· умова задачі містить актуальну проблему суспільства, але не вистачає даних, які б зв‘язали засвоєний раніше матеріал з описаною ситуацією;
· відбувається аналіз фактів дійсності, співставлення життєвих уявлень та наукових понять, переклад побутової мови на мову науки;
· висуваються гіпотези розв‘язання, робляться висновки, а далі відбувається дослідна перевірка;
· задача подається в незвичній для учнів формі (наприклад, містить данні в таблиці, у вигляді діаграм тощо).
Для досягнення активізації пізнавальної діяльності в процесі роботи над задачею потрібно підвищувати пізнавальний інтерес дитини. Це можливо зробити шляхом створення проблемних ситуацій. Головна мета їх використання – підняти рівень засвоєння понять; навчити системі розумових дій для розв’язання творчих нестандартних задач та проблем створених життям.
Пізнавальна активність та самостійність школярів збільшується завдяки різноманітності елементів навчального процесу. Цього вимагає і модернізація уроку.
Введення проблемного методу в навчання, як стверджує М.І. Махмутов [40], можливе за умови , коли виділяються такі структурні елементи уроку:
· актуалізація раніше засвоєних знань, вмінь та навичок;
· створення проблемних ситуацій та постановка проблеми;
· розумовий пошук та розв‘язання проблеми (висування та доведення гіпотез);
· перевірка розв‘язку проблеми.
При цьому зазначається, що структура проблемного уроку, або уроку, що містить проблемний підхід, може значно варіюватись. В кожному окремому випадку вона визначається логікою учбового процесу, етапами творчої діяльності та рівнем проблемності.
Модернізація уроку, в ході якого розв’язуються математичні задачі фінансового змісту, відбувається завдяки врахуванню особливостей роботи над цим видом задач.
Важливе значення для активізації пізнавальної діяльності учнів, підвищення інтересу до математики та формування пізнавальної самостійності має і правильна організація самостійної роботи учнів. Завдяки їй можливе підвищення свідомості та міцності знань учнів при навчанні математики, а також формування глибини та свідомості знань, вмінь та навичок, розвиток пізнавальних здібностей. Це і спостережливість, допитливість, логічне мислення, творча активність тощо. Глибоке засвоєння знань та їх усвідомлення можливо лише в процесі самостійної роботи. Тут учень знаходить нові зв‘язки між отриманими знаннями, застосовує їх у нових умовах, пізнає раніше невивчені сторони явищ та поповнює свої знання.
Самостійна робота присутня на всіх етапах навчання. Це позитивне явище дає можливість для досягнення головної мети навчання – формування всебічно розвиненої особистості, готової до життя в сьогоднішніх умовах.
В залежності від різних основ, які покладені в класифікацію, самостійні роботи поділяють за принципом дидактичного призначення самостійних робіт у навчанні (самостійні роботи, які використовуються для отримання нових знань; самостійні роботи для використання нових знань, на утворення вмінь та навичок; самостійні роботи з метою перевірки знань та їх повторення) [19]; за джерелом знань (робота з підручником; робота з довідковою літературою; учбові вправи; твори та описи; лабораторні роботи; роботи, які пов‘язані з використанням карт, схем, малюнків, графіків тощо) [51]; за способами управління викладачем навчальною діяльністю учнів (роботи під керівництвом вчителя; робота з посібниками; практичні роботи; повністю самостійні роботи; творчі роботи).
У всіх зазначених класифікаціях, на жаль, не враховується просування до вищого рівня розумової діяльності, перехід до вищого рівня активності та самостійності учнів. Виходячи зі структури пізнавальної діяльності та єдності її процесуальної сторони з логіко-змістовною, П.І. Підкасистий [43] запропонував таку типологію самостійних робіт:
· відтворюючі самостійні роботи за зразком;
· реконструктивно-варіативні самостійні роботи;
· евристичні самостійні роботи;
· творчі самостійні роботи.
Ця типологія має велике значення для активізації пізнавальної діяльності учнів, та ми її враховували при розв‘язуванні математичних задач фінансового змісту. Розглянемо детальніше ці типи.
При виконанні самостійних робіт першого типу, самостійність знаходиться повністю в рамках відтворюючої діяльності. Учень діє за зразком, схожою ситуацією чи детальним інструктажем. Коли учбовий матеріал усвідомлений учнем, він легко відтворюється ним без певних змін. При виконанні самостійної роботи, учень дізнається про деякий факт, явище, згадує зразок діяльності для розв‘язування запропонованої задачі та розв‘язує її. Покажемо це на прикладі розв’язання наступної задачі:
Задача. Ціна реалізації продукції, яка включає податок на додану вартість обчислюється за формулою
Ц = ( С + П ) × 1,2 (1.1)
де Ц –ціна реалізації, С – собівартість товару, П – прибуток. Знайти прибуток, який планує отримати підприємство від реалізації 100 автомобілів за ціною 5 000 у.о., якщо собівартість одного автомобіля становить 3 500 у.о.
Розв’язуючи її, учень згадує правила перетворення формул, виводить формулу обчислення прибутку та, підставляючи данні задачі в отриману формулу, виконує обчислення.
До цього типу належить більшість тренувальних задач на закріплення. Від учнів не вимагається реконструкції в умові задачі, бо висновок міститься в самих її посиланнях. Така самостійна робота сприяє накопиченню основних фактів і способів діяльності, вмінь та навичок. Але при цьому діяльність учнів не має бути механічною, вони повинні вміти теоретично обґрунтовувати кожний свій крок, усвідомлювати усі нові засвоєнні дії. Самостійна робота такого типу не залучає учня в пошукову діяльність, не розвиває творчих здібностей та не формує досвіду роботи в змінених умовах. Однак такі роботи необхідні для включення учня в подібну ситуацію, бо без знань основних фактів та способів дій не можливо організувати роботу на вищому рівні.
Наступний рівень пізнавальної самостійності учнів - дії в змінених ситуаціях, де потребується реконструкція вже відомих знань, даних задачі тощо. На базі досвіду діяльності за зразком учень усвідомлює внутрішню структуру матеріалу, умову та вимогу задачі, проводить узагальнення, застосовує узагальнені данні для подальшої роботи. Завдяки цьому знання поглиблюються, стають усвідомленими, розширюється сфера їх застосування. Узагальнення, отримані завдяки усвідомленням учнями структури знань та зв‘язків між ними, є ефективним засобом при виконанні завдань, які містять різні варіації в їх умові та вимогах.
Діяльність вказаного рівня здійснюється при розв’язанні задач реконструктивно-варіативного характеру. Наведена вище задача на цьому етапі може бути сформульована наступним чином:
Задача. Податок на додану вартість в Україні становить 20% від ціни товару (робіт, послуг). Ціна товару виробника включає в себе собівартість товару та прибуток, який отримає підприємство від його продажу. Як обчислити ціну реалізації товару, якщо вона включає в себе ціну товару виробника та ПДВ?
При роботі з такими задачами учні готуються до пошукової діяльності. При цьому вони отримують досвід використання вже відомих явищ, отримання узагальнень та висновків із роботи.
Стимулююча роль постановки математичних проблем перед учнями в плані розвитку їх інтелекту та знань у фінансово-економічної сфері показує, що радість відкриття завжди збільшує інтерес до навчання та підвищує результативність навчального процесу.
Евристична самостійна робота спрямована на навчання учнів пошуковій діяльності, виявленню залежностей між знаннями, пошуку нового способу розв‘язування задач та розв‘язанню проблемних ситуацій, які створюються вчителем під час роботи або які виконають під час роботи з задачами. Завдання для таких робіт повинні бути такими, щоб учням доводилось розв‘язувати лише окремі під проблеми, а не всі проблеми відразу. В наслідок виконання таких математичних дій учні опановують елементи творчості, вчаться орієнтуватися в складних ситуаціях, оволодівають евристичними прийомами та здійснюється перехід від відтворюючої діяльності до творчої.
В нашому випадку математична задача фінансового змісту, яка використовується для евристичної самостійної роботи, може бути сформульована таким чином:
Задача. Як обчислити ціну, за якою реалізується товар, якщо податок на додану вартість становить в Україні 20 % ціни товару виробника?
Для розв‘язання її необхідно встановити залежність між такими величинами, як ціна товару виробника, податок на додану вартість, ціна реалізації товару. В умові задачі не показано зв’язок ПДВ та ціни реалізації, тому лише в ході логічних міркувань учні встановлюють, що уникнення втрати від продажу товару та виплати ПДВ, потрібні гроші, які включають ПДВ в ціну реалізації товару. Після чого треба скористатися математичними знаннями про обчислення відсотків та вивести шукану формулу.
При цьому учні повинні володіти евристичними прийомами, знати теоретичний матеріал та вміти застосовувати його до розв‘язування проблем. Тут діяльність учнів має гнучкий характер без чіткого алгоритму.
Під творчою роботою будемо розуміти таку роботу, яку учень виконує повністю самостійно за складеним ним докладним планом, коли учень відкриває або творить щось нове для себе. Наприклад, до творчих завдань можна віднести задачі на знаходження різних способів розв‘язування та завдання на складання нових задач.
У нашому дослідженні в цю групу ми включаємо роботи, виконання яких потребує творчої самостійності учнів, а також наявність:
· елементів творчого мислення (бачення проблеми, встановлення гіпотетичних зв’язків, висунення гіпотез, їх перевірка, погляд на проблему в цілому і т.д.);
· розвинутої інтуїції;
· вмінь розв’язувати задачу різними способами;
· вибору раціональних шляхів розв’язання;
· розуміння закономірностей складання математичних задач певного типу;
· вмінь користуватися відповідною літературою, вибирати необхідний матеріал, деяких конструктивних і практичних вмінь.
Для успішного виконання як творчих, так і евристичних робіт необхідна сформованість вмінь діяти за зразком або за загальним правилом у зміненій ситуації. З іншого боку, творча діяльність формує інтерес учнів до математики, стимулює пізнавальну активність, формує особистісні якості та сприяє підвищенню ефективності навчання.
В ході вивчення математики дуже корисно пропонувати учням такі творчі самостійні роботи, які передбачають пошук використання математичних знань у фінансовій сфері.
Характер задач та рівень їх складності, якими наділяється самостійна робота, повинні змінюватись у процесі навчання. Це обумовлено організацією таких самостійних робіт, при виконанні яких учні засвоюють не лише систему тих знань, вмінь та навичок, які передбачені програмою, але й опановують методами пізнання, розвивають творчі здібності та вміння застосовувати знання в життєвих ситуаціях. Для того, щоб відкрити щось нове, самостійно працювати над задачами, поповнювати власні знання та знаходити різні шляхи діяльності, необхідно мати певний запас вже отриманих знань і способів діяльності. Тому велике значення має робота учнів з математичними задачами фінансового змісту на репродуктивному рівні. Школярі повинні засвоїти певні фінансово-математичні закони та операції через відтворення, а не через самостійне їх відкриття. Цього вимагають і обмеженість часу, і сам процес навчання. Це повинно також враховуватись і при організації самостійних робіт із математичними задачами фінансового змісту. Важливо передбачити, щоб відтворюючі та творчі процеси в самостійній роботі отримали оптимальне співвідношення, щоб учні просувались до вищих рівнів розумової діяльності.
Робота над задачею може здійснюватись у різних формах: фронтальній, груповій та індивідуальній. Фронтальна – використовується при розв‘язуванні проблемних ситуацій всім класом, при навчанні методам розв‘язування певного класу задач та при поясненні нового матеріалу. Групова передбачає роботу за групами, які можуть бути створені за різними принципами. В умовах одного класу для досягнення вищого рівня знань, вмінь та навичок можна виділити такі критерії розподілу на навчальні групи:
· рівень сформованих знань, вмінь та навичок, оскільки процес засвоєння залежить від накопичуваного досвіду;
· рівень здатності до навчання, яка полягає в здатності узагальнювати, абстрагувати тощо;
· рівень пізнавального інтересу;
· рівень пізнавальної активності та самостійності.
Враховуючи окреслені вище критерії, як правило, в класах виділяють три типологічні групи: з низьким, середнім та високим рівнем навчальних можливостей. Навчальна діяльність учнів різних типологічних груп організовується за допомогою різних методів та прийомів навчання. Розподіл учнів на групи дає можливість впроваджувати групову роботу.
Індивідуальна форма навчання полягає у виконанні завдань кожним учнем окремо та самостійно. Завдання можуть бути однакові або різні, в залежності від можливостей та зацікавленості школярів.
Як зазначалось вище, підвищенню ефективності та активізації пізнавальної діяльності учнів сприяє не один метод, а їх логічне поєднання. Тоді вони забезпечують просування учнів від простої репродуктивної діяльності до найвищого рівня – творчої активності. Так, для слабких учнів можливе поєднання пояснення та виконання завдань під керівництвом вчителя, для середніх – проблемний підхід при викладенні матеріалу та напівсамостійне виконання завдань, а для сильних – постановка проблеми та самостійне її розв’язання, подальше її застосування в житті та самостійне складання задач.
Комп’ютерна підтримка навчально-пізнавальної діяльності учнів збільшує можливості для створення та розв’язування математичних задач фінансового змісту. Зокрема, використання Інтернет–сайтів для знаходження певної фінансової інформації дозволяє швидко та аргументовано знаходити математичні данні та залежності різних фінансових величин. Надаючи учням можливості самостійного створення математичних задач фінансового змісту, вчитель активізує пізнавальну діяльність учнів та привчає до сучасних засобів пошуку інформації. Важливо зазначити, що ознайомлення учнів з використанням Інтернет-сайтів є достатньо багатогранною діяльністю. Наявність великої кількості сайтів в Інтернеті може забрати багато часу для відшукання необхідної інформації, тому для початкового ознайомлення учнів із таким процесом навчальної діяльності варто запропонувати декілька корисних інтернет–адрес.
Для самостійного створення математичних задач фінансового змісту ми в ході експерименту запропонували учням такі інтернет – адреси:
Банки
www.worldbank.org - сайт світового банку;
www.cbr.ru – сайт Центрального банку РФ;
www.nbu.gov.ua – сайт Національного банку України;
Податки
www.sta.gov.ua - сайт Податкової служби України;
www.nalog.ru - сайт Міністерства РФ по податкам та зборам;
Цінні папери
www.minfin.gov.ua - сайт Міністерства фінансів України;
http://www.kmu.gov.ua - сайт Кабінету міністрів;
http://www.minfin.ru - сайт Міністерства фінансів Росії;
www.finam.ru - сайт фінансових ринків;
Сімейний бюджет
www.rada.gov.ua - сайт Верховної Ради України;
www.ifin.ru – сайт, присвячений фінансовим технологіям та послугам;
Страхування
www.minfin.crimea.ua – сайт Міністерства Фінансів АР Крим;
http://finance.com.u a ;
Різне
www.fincom.spb.ru - сайт Комітету фінансів адміністрації Санкт - Петербурга;
www.m3m.ru - Фінансовий словник;
www.cfin.ru - бібліотека з менеджменту, маркетингу та фінансів;
www.aup.ru – сайт з економіки та фінансів;
www.ipssr.kiev.ua – Державна академія статистики, обліку та аудиту;
www.csrs.ru - сайт центру досліджень та статистики Міністерства науки Росії;
stat.if.ukrtel.net - Івано-Франківське обласне управлiння статистики.
Дослідження підтвердили ефективність такої організації навчального процесу. Під час роботи з комп’ютером учні стають активними суб’єктами власної навчальної діяльності. Вони вільні обирати для себе таку інформацію, яка їх більше зацікавлює та захоплює. З іншого боку, така форма організації навчання стимулює учнів до розширення власних знань, вмінь та навичок, що сприяє всебічному розвитку особистості.
Отже, спираючись на принципи дидактики, враховуючи досвід результатів розробки цього питання іншими дослідниками та розв'язуючи задачу підвищення активізації пізнавальної діяльності учнів основної школи при розв’язуванні математичних задач фінансового змісту, ми виділили такі прийоми та методи організації роботи з ними:
1. Використання елементів проблемного навчання: задач з зайвими даними, задач із недостачею даних, задач із не сформульованим запитанням, задач з декількома розв‘язками, задач на логічне міркування тощо.
2. Самостійність у роботі з математичними задачами фінансового змісту.
3. Створення математичних задач фінансового змісту учнями.
4. Використання практичних досліджень ринкових відносин.
5. Диференційованість у навчанні, різнорівневі завдання у відповідності до можливостей учнів.
6. Організація групової роботи з математичними задачами фінансового змісту.
7. Використання різних реальних фінансових даних та їх пошук завдяки комп’ютерним технологіям.
Правильний вибір методів та прийомів навчання передбачає врахування як змісту учбового матеріалу, так і рівня його складності й специфіки підготовки учнів.
Активізувати навчально-пізнавальну діяльність можливо завдяки спрямуванню навчання не на догматичне засвоєння готових знань, а на активне добування їх учнями в результаті оперування ними, пошуку способів їх використання та одержання нових знань. Це можливо досягти завдяки використанню різних методів та прийомів учбової діяльності. Питання вибору шляхів активізації пізнавальної діяльності учнів дуже пов'язане з встановленням раціонального відношення між методами та прийомами, які використовуються в процесі навчання.
РОЗДІЛ 2. Методичні рекомендації щодо використання математичних задач фінансового змісту для активізації пізнавальної діяльності учнів
2.1. Використання задач на банківські розрахунки в основній школі
Розвиток ринкових відносин розширює сферу діяльності банків. Необхідними чинниками досягнення позитивних результатів у напрямку економічного пожвавлення є свідоме ставлення громадян України до необхідності правового забезпечення стабільного розвитку і діяльності банків в Україні, бо через банківську систему здійснюється основна кількість всіх фінансових розрахункових операцій.
Розуміння актуальності роботи банківської системи сьогодні є необхідною умовою для адаптації громадянина в суспільному житті. Клієнти банків передають йому в управління свої кошти в разі розміщення грошей на депозитних вкладах. Через банки здійснюються розрахунки за надані комунальні послуги, поширеним стає отримання заробітної плати, пенсій та стипендій через розрахунки за допомогою платіжних банківських карт. Послуги банків набувають все більшого поширення та мають велику кількість переваг. Користування такими послугами має бути зрозумілим для пересічних громадян. Виникає необхідність належним чином роз’яснити переваги банківської системи в сфері грошового обігу, захисту власних заощаджень та зручності під час здійснення розрахунків. Основи розуміння особливостей діяльності банків з громадянами (банківського всеобучу) сьогодні можна і необхідно закладати в школі на уроках математики шляхом включення в зміст освіти задач на банківські розрахунки та концентрувати увагу учнів на їх важливості у житті.
Розглянемо звичайну фінансово-математичну проблему, яка сьогодні постає перед багатьма членами нашого суспільства - особливості грошового вкладу в банк. Сьогодні можна знайти деякі задачі з даної тематики у шкільних підручниках, але нажаль їх кількість дуже обмежена і вони не розкривають всіх необхідних аспектів банківської діяльності, з якими зустрічається кожний громадянин та які можуть бути розкриті у курсі математики основної школи.
Одним із видів діяльності банків є виконання валютних фінансових операцій. У нашій країні національною валютою є гривня. Проте часто громадяни України мають справу з такими іноземними валютами, як долар США, російський рубль, євро, японська ієна тощо. Учбові задачі можуть це проілюструвати. Наприклад, в ході ознайомлення учнів дев’ятого класу з темою “Елементи прикладної математики” можливо запропонувати таку задачу:
Задача 1. В таблиці наведені дані про курси гривні встановлені Національним банком України по рокам:
| Кількість гривень за 100 одиниць іноземної валюти | ||||||
| На 1.11.1997 | На 2.11.1998 | На 1.11.1999 | На 31.10.2000 | |||
| Німецька марка | 103 | 342 | 245 | 233 | ||
| Японська єна | 15 | 207 | 245 | 233 | ||
| Долар США | 187 | 342 | 453 | 543 | ||
1) розрахуйте ціну гривні в іноземній валюті кожного року
Методика розв’язання цієї задачі може бути такою. Спочатку учням пропонується самостійно виконати це завдання. Після одержання даних в одній валюті – гривнях, клас колективно виконує вимогу задачі.
Робота з такими величинами привчає учнів до виконання правила порівняння одноімених величин, а також ознайомлює з різними найпоширеними національними валютами світу.
Введення поняття “іноземна валюта” через задачі на уроках математики активізує увагу учнів до запропонованої тематики, розширює їх світогляд та формує знання про іноземну валюту як засіб законного платежу на території відповідної іноземної держави з можливістю вільної конверсії у банківсько-кредитних установах на території України.
У дев‘ятому класі, під час вивчення теми “Відсоткові розрахунки” вчитель може створити проблемну ситуацію, яка збуджує емоції учнів та зацікавлює в пошуку відповіді на таку життєво важливу задачу: “Яка загальна формула нарахування відсоткових грошей в банку, якщо в банк покласти S0 гривень під р % на n років, а відсотки нараховуються один раз на рік?” Пошук відповіді на це завдання проводить до виведення формул простого та складного відсотку за допомогою послідовних відповідей на такі запитання:
1. Яка сума нараховується на вклад через 1 рік?
2. Яка сума з‘являється на вкладі через 1 рік?
3. Які відсоткові гроші нараховуються на 2-ий рік?
4. Яким стане вклад через два роки з врахуванням початкової суми вкладу?
Далі, проводячи аналогічні міркування про третій та четвертий роки, учні помічають закономірність між зміною суми вкладу, кількістю років та відсотковою ставкою банку. В результаті, виводяться формули:
![]() - формула
складного відсотку, (2.1)
- формула
складного відсотку, (2.1)
![]() - формула
простого відсотку, (2.2)
- формула
простого відсотку, (2.2)
де Sn – сума вкладу після n нарахувань,
S0 – початкова сума вкладу,
p – відсоткова ставка банку,
n – кількість нарахувань
Для сильних учнів, які знайомі з методом математичної індукції, можна запропонувати довести одержані формули відповідним методом.
Обов‘язково потрібно провести порівняльний аналіз цих формул та звернути увагу учнів на те, що відсотки називають простими, якщо нарахування відбуваються постійно на початковий капітал, а складні відсотки нараховуються на капітал, який утворюється протягом певного періоду.
Особливість нарахувань відсотків щомісячно можна проілюструвати на прикладі:
Задача 3. Обчислити відсоткові гроші у випадку вкладу 1000 грн. під 12 % річних, якщо відсотки нараховуються кожного місяця.
Перед розв’язанням задачі учні колективно шукають відповідь на запитання: Як знайти відсоткову ставку щомісячних нарахувань, якщо відома річна відсоткова ставка?
Для закріплення цього факту учням пропонується за даними задачі відповісти на запитання, якщо відсотки нараховуються кожного півріччя, кожного кварталу, кожного місяця. Після цього можна запропонувати самостійну роботу на виведення формули нарахувань відсоткових грошей, якщо відсотки нараховуються кожного півріччя, кожного кварталу, кожного місяця. Робиться висновок, що під n у формулі розуміється кількість періодів нарахування відсотків.
Для порівняння дії цих формул корисно запропонувати учням самостійно знайти складний відсоток, щоб через три роки на вкладі була така ж сама сума грошей, як і при простому відсотку нарахувань. Таке завдання активізує учнів та вчить порівнювати результати нарахування відсоткових грошей, аналізувати математичні данні.
Сформованість вмінь учнів дев’ятого класу розв‘язувати квадратні рівняння дає змогу розв’язувати задачі, які показують можливе використання послуг банку для власного планування грошових витрат. Це можуть бути, наприклад, задачі такого змісту.
Задача 4. На початку року є можливість внести в банк на рахунок 1640 гривень, але в кінці року треба зняти з рахунку 882 гривні, а через рік знову - 882 гривні. Під який відсоток потрібно внести гроші в банк, щоб вказані операції відбулися?
Початкова робота з даними цієї задачі потребує повторення фінансових понять – початковий вклад, відсоткові гроші, відсоток та прибуток.
Математичні залежності між цими величинами дають можливість пояснити данні задачі у вигляді тверджень: 1640 грн. – початковий вклад для першого року. Нехай х % - щорічні відсоткові нарахування банку. Тоді на кінець року банк нарахував (0,01х×1640) грн., і на рахунку стало
(1 640 + 0,01х × 1 640) грн. або (1 640 × (1 + 0,01х)) грн.
На початку другого року вклад становив
(1 640 × (1 + 0,01х) - 882) грн.
На цю суму було нараховані (0,01х × (1 640 × (1 + 0,01х) - 882)) грн. - відсоткові гроші, а сума, яка була на рахунку на кінець другого року, становила ((1 640 × (1 + 0,01х) - 882) + 0,01х × (1 640 × (1 + 0,01х) - 882)) грн., або ((1640(1+0,01х)-882)(1+0,01х)) грн., що за умовою задачі дорівнює 882 грн.
Отримаємо рівняння:
(1640 × (1 + 0,01х) - 882)(1 + 0,01х) = 882.
Введемо нову змінну у = 1 + 0,01х. Тоді рівняння має вигляд:
(1640у - 882) × у = 882;
1640у2 - 882у - 882 = 0;
820у2 - 441у - 441 = 0.
Розв‘язуючи отримане квадратне рівняння, знаходимо:
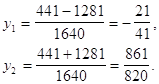
Повертаючись до
змінної х, зазначаємо, що значення у1 не задовольняє умову задачі.
Тому 1 + 0,01х =![]() , а х = 5 (%).
, а х = 5 (%).
Відповідь: 5%.
Методика розв’язування таких задач, як бачимо, традиційна. Це забезпечує успіх у їх використанні. Одночасно з удосконаленням вмінь розв’язувати квадратні рівняння учні здобувають первинні фінансові знання та з’ясовують для себе питання “вдалого” вкладу. Вони шукають найкращий варіант для збереження грошей – можливість отримати потрібний прибуток із певної кількості грошей.
Крім цього учні отримують інформацію і про те, що депозитний вклад - це кошти в готівковій або у безготівковій формі, у валюті України або в іноземній валюті, які розміщені клієнтами на їх іменних рахунках у банку на договірних засадах на визначений строк зберігання або без зазначення такого строку і підлягають виплаті вкладнику відповідно до законодавства України та умов договору [20].
Дуже часто банки пропонують різні види депозитного вкладу. Ознайомлення учнів із особливостями вкладів на депозитний рахунок, як показав експеримент, можна здійснити на уроці математики в 9класі під час вивчення теми “Відсоткові розрахунки”. Для цього учням у ході експерименту було запропоноване попереднє домашнє завдання, яке полягало в знаходженні різних умов вкладів до банків. На уроці було визначено як краще вкласти 1000 гривень на один рік. Кожен учень рахував прибуток, який буде отриманий за один рік, якщо всі гроші відразу покласти до банку та отримувати відсоткові гроші а)щомісяця, б) в кінці дії договору, та якщо вклад поповнювати через певні проміжки часу, наприклад щомісяця або щоквартально. Цікавим прикладом була пропозиція одного з банків про вклад “дитячий”, де банком, крім запропонованих відсоткових грошей, пропонувалась премія при закритті рахунку в термін, обумовлений договором, яка обчислювалась як сума відсоткового доходу, помножена на відсоток, що дорівнює середньому балу успішності.
Таким чином, учні мають можливість познайомитись із особливостями депозитних вкладів у банках та спробувати самостійно здійснити розрахунки кількості власних грошей, які можуть бути покладені на депозитний рахунок.
Різні умови вкладів дають можливість застосовувати фінансові операції, навіть на етапі мотивації вивчення нового матеріалу на уроці. Так, у дев’ятому класі ознайомлення учнів із використанням геометричної прогресії ми провели на прикладі вкладу з обов’язковим поповненням.
Задача 5. Обчислити суму вкладу та прибуток, якщо банк пропонує умови вкладу, відображені в таблиці 2.1, а вкладник планує покласти 1000 гривень на два роки з поповненням по 1000 гривень щоквартально.
Таблиця 2.1
Основні умови вкладу (до задачі)
| Мінімальна сума вкладу | 500 гривень | |||
| Мінімальна сума поповнення | 100 гривень | |||
| Дохідність ( %, річні) | 6 місяців | 9 місяців | Більше 13 місяців | |
|
До 10000 грн. |
10 % | 11 % | 12 % | |
| Більше 10000 грн. | 12 % | 13 % | 15,5 % | |
| Нарахування відсотків | Щоквартально | |||
| Обов’язкове поповнення | Кожні три місяця |
Це задача із зайвими даними. Учні, в першу чергу, повинні прийняти правильне рішення щодо виконання умов банку. Таким чином, для роботи маємо такі данні:
· Термін дії договору – два роки,
· Сума вкладу – 1000 гривень із щоквартальним поповненням у 1000 гривень,
· Відсоток банку – 12 % щорічно, або 12 : 4 = 3 % щоквартально.
Ці данні можуть бути зображені за допомогою мал.2.2 та продемонстровані учням за допомогою кодоскопа.

Мал. 2.2. Виконання умов договору (до задачі)
Аналіз мал.2.2 повинен включати визначення етапів нарахування відсотків. Маємо таку схему нарахування грошей:
· на останній внесок відсотки нараховується лише один раз, тому з цього внеску вкладник буде мати на кінець дії договору:
1000 + 1000 × 0,03 = 1000 × (1 + 0,03) = 1000 × 1,03;
на шостий внесок (передостанній) відсотки нараховуються два рази, тому з цих грошей на кінець дії договору:
1000 + 1000 × 0,03 + (1000 + 1000 × 0,03) × 0,03 =
1000×(1 + 0,03) + 1000×(1 + 0,03)×0,03 = 1000×(1 + 0,03)(1 + 0,03) = 1000×1,032;
· з п’ятого внеску – 1000 × 1,033, бо відсотки нараховувались три рази;
· ...
· з першого внеску – 1000 × 1,038.
Отримали геометричну прогресію, у якої знаменник дорівнює q = 1,03, перший член (останній внесок) b1= 1000, а кількість членів n =8.
Таким чином, вкладник у кінці дії договору має таку суму грошей:
S =1000×1,03 + 1000×1,032 + 1000×1,033 +...+ 1000 × 1,038.
Для обчислення значення цього виразу скористаємось формулою суми геометричної прогресії:
![]() = 8 892,34
(грн.).
= 8 892,34
(грн.).
Після обчислення значення отриманого виразу, учнів потрібно ознайомити з фінансовими термінами, які використовувались для отримання результату, а саме:
· ануїтет - послідовність однакових внесків, зроблених через рівні проміжки часу,
· інтервал сплати – проміжок часу між двома послідовними платежами,
· строк ануїтету – час, від першого до останнього платежу.
Робота з такими даними показує учням застосування властивостей геометричної прогресії в банківських розрахунках.
При подальшому вивченні властивостей геометричної прогресії може бути розглянута проблемна задача, яка показує діяльність системи банків у нашій державі.
Задача 6. Вклади населення України в комерційних банках з 1995 року в національній валюті кожного року збільшуються приблизно в 2 рази, а у іноземній валюті – в 1,5 рази. В 1995 році вклади населення в комерційних банках в національній валюті становили 505 млн. грн., а в іноземній – 111 млн. грн. Чи буде загальна кількість вкладів утворювати геометричну прогресію, і якщо так, то який у неї буде знаменник?
Розглянемо один з можливих варіантів її розв’язання. Пропонуємо учням заповнити таблицю 2.2 наближених даних по вкладам населення України в комерційних банках з 1995 до 2000 року.
Таблица 2.2
Вклади населення України в комерційні банки, млн. грн.
| 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | |
| В національній валюті | 505 | |||||
| В комерційній валюті | 111 | |||||
| Всього |
Для інтенсифікації роботи учнів доцільно заготувати шаблон таблиці та роздати до початку роботи. При цьому початкові данні таблиці можуть мати певні розбіжності, оскільки данні задачі є наближеними до реальних даних, однак не остаточними.
Для активізації пізнавальної діяльності учнів варто заповнення таблиці організувати у вигляді змагання на кращого фінансиста. Далі учням пропонується проаналізувати отримані числа та зробити потрібні висновки.
Заповнення таблиці проводиться кожним учнем самостійно, але аналіз отриманих даних потрібно зробити колективно та звернути увагу учнів на важливість математичних закономірностей у реальному житті. Обов’язково треба звернути увагу учнів на те, що данні про вклади в іноземній валюті наведені в гривнях. Чому?
Якщо роботу проводити на вищому рівні складності, то аналіз задачі приводить до формули загальної кількості всіх вкладів у комерційних банках, тобто:
формула n - ного члена прогресії вкладів у національній валюті - 505×2n;
формула n - ного члена прогресії вкладів у комерційній валюті - 111×1,5n.
Тоді формула n - ного члена прогресії всіх вкладів – 505×2n+111×1,5n.
Ця задача показує учням, що довіра у людей до роботи з комерційними банками нашої держави поступово зростає. Наведена робота відповідає такому типу проблемних задач, як задача з декількома можливими способами розв’язання.
Отже, при розгляді задач про діяльність банків, яка пов‘язана з депозитними вкладами, потрібно виділити такі величини:
1. Початковий капітал.
2. Відсоткова ставка.
3. Прибуток ( відсоткові гроші).
4. Термін вкладу (час).
5. Результативний капітал.
Робота банків не обмежується лише депозитними вкладами, тобто залученням коштів клієнтів із виплатою їм відсоткової ставки. Банки також кредитують клієнтів, тобто надають кошти у користування юридичним або фізичним особам на визначений строк із отриманням прибутку у вигляді процентів, які сплачує клієнт за користування кредитом.
Дуже часто в діяльності банків зустрічається надання коштів у кредит з умовою послідовної виплати суми кредиту за певний проміжок часу.
В нашій державі все більших обертів набирає споживчий кредит, який в свою чергу стає ланкою витрат сімейного бюджету. Споживчий кредит - це кошти та матеріальні цінності, які надаються громадянам для придбання, замовлення та використання товарів (робіт, послуг) для власних побутових потреб на визначений строк та під встановлені проценти. Прикладом отримання споживчого кредиту є кредит на певний проміжок часу з щорічними (щомісячними, щоквартальними) виплатами кредиту та нарахуванням відсотків на суму, яка залишилась не виплаченою. При розгляді властивостей арифметичної прогресії учням запропоновано порівняти величини відсоткових грошей такого кредитування та кредитування, коли відсотки нараховуються завжди на суму кредиту.
Задача 9. Кредит отриманий на 12000 грн. під 10 % річних на залишок кредиту на 12 років з щорічною виплатою 1/12 частини кредиту. На скільки зміняться відсоткові гроші виплати кредиту, якщо взяти цю ж суму на той самий строк під 10 % від суми кредиту?
Для знаходження відповіді на запитання задачі клас доцільно розподілити на дві групи: сильніші учні та слабкі. Для групи з сильніших учнів запропонувати обчислити відсоткові гроші за умови взяття кредиту в задачі, а для групи слабких учнів – за умови запитання задачі.
Міркування сильної групи доцільно спрямувати на складання послідовності щорічних виплат отриманого кредиту:
Кожного року залишок кредиту зменшується на
12 000 × 1/12 = 1 000 (грн.).
Тоді відсоткові виплати за 1 рік становлять
(12 000 – 1 000)×0,1 = 1 100(грн.)
за другий рік – (12 000 – 2 × 1 000)×0,1 = 1 000 (грн.),
за третій рік – (12 000 – 3 × 1 000)×0,1 = 900 (грн.),
...
за одинадцятий рік – (12 000 - 11×1 000)×0,1 = 100 (грн.)
за дванадцятий – 0 грн.
Отже, отримали арифметичну прогресію, різниця якої 100 грн. Тому для обчислення всіх відсоткових грошей скористаємось формулою суми арифметичної прогресії:
![]() = 6 600 (грн.)
= 6 600 (грн.)
Міркування слабкіших учнів доцільно спрямувати наступним чином: якщо взяти 12000 грн. на 12 років під 10 % річних на суму кредиту, то відсоткові виплати будуть дорівнювати
12 000 × 0,1 = 1 200 (грн.) щорічно,
а років - 12, тому всі відсоткові виплати дорівнюють:
1 200 × 12 = 14 400 (грн.).
Аналіз та порівняння отриманих даних проводиться колективно. Після чого робиться висновок, що виплати більші на
14 400 – 6 600 = 7 800 (грн.).
Також доцільно учням самостійно запропонувати визначити таку відсоткову ставку кредиту без щорічних виплат, щоб відсоткові виплати були однаковими у двох випадках.
Для учнів, які цікавляться математикою, доцільно запропонувати вивести формулу обчислення відсоткових грошей кредиту, який отриманий на S грн. під р % річних на залишок кредиту на n років з щорічною виплатою рівних частин кредиту.
Учні вчаться рахувати власні витрати при використанні різних видів кредитів, які поширені в нашій державі.
У нашій державі існує розгалужена банківська система. Тому найчастіше люди проводять грошові операції зі своїми коштами через декілька різних банків. Так, наприклад, під час вивчення теми "Розв‘язування задач за допомогою рівнянь" учням може бути запропонована така задача.
Задача 10. Яку загальну суму кредитор повинен покласти в три різні банки, щоб виконувались умови: в банк "А" потрібно покласти 45% від вкладу в банк "В", а сума вкладу в банк "В" становить 80% від вкладу в банк "С", а в банк "С" він вклав суму, яка перевищує вклад в банк "А" на 6 400 гривень?
Розв‘язування цієї задачі може бути проведено за такою схемою. Спочатку потрібно звернути увагу учнів на вклади, зроблені в різні банки. За умовою задачі вклади мають між собою математичну відсоткову залежність, хоча в житті бувають різні ситуації і не завжди між банківськими вкладами спостерігається математична залежність або закономірність.
Для перекладу даних задачі на математичну мову, учням самостійно пропонується записати залежність між вкладами в різні банки за допомогою математичних виразів. Виконуючи це завдання, учні приходять до висновку, що для виконання цього завдання доцільно ввести змінну х гривень - сума вкладу в банк "С". Тоді в банк "В" потрібно покласти 0,8х гривень, а в банк "А" - 0,36х гривень. Вклад у банк "С" перевищує вклад у банк "А" на (х - 0,36х) гривень, що за умовою задачі дорівнює 6 400 гривень. Отже, в результаті наведених міркувань отримаємо рівняння з однією змінною:
х - 0,36 × х = 6 400;
0,64 × х = 6 400;
х = 10 000 (грн.).
Тоді вклад у банк "В" дорівнює:
0,8 × 10 000 = 8 000 (грн.),
а вклад у банк "А":
0,36 × 10 000 = 3 600 (грн.).
Загальна сума, вкладена кредитором в банки:
3 600 + 8 000 + 10 000 = 21 600 (грн.).
Підбиваючи підсумковий аналіз цієї задачі, потрібно звернути увагу учнів на велику мережу банків, що працюють в Україні. Вони утворюють дворівневу банківську систему держави (мал.2.4):
 Національний
банк України
Національний
банк України
комерційні та спеціалізовані банки
Мал.2.4. Банківська система держави
Національний банк України є головним банком країни. Він проводить єдину кредитно-грошову політику, організовує міжбанківські розрахунки, забезпечує стабілізацію національної валюти та координує роботу всіх комерційних банків. До компетенції комерційних банків віднесено такі функції:
1. кредитно-розрахункове обслуговування підприємств, організацій, населення;
2. касове обслуговування підприємств, організацій, населення;
3. операції з іноземною валютою;
4. інші, визначені законодавством.
За законом про банки і банківську діяльність [20]кожний комерційний банк зобов’язаний частину коштів відраховувати до Національного банку України для створення стабілізаційного фонду. Це обов‘язкові резерви банків. Вони встановлюються як певний відсоток від суми коштів, якими володіє комерційний банк. Решта коштів – вільний резерв, якими банк розпоряджається самостійно.
Для ілюстрації цього учням може бути запропонована така задача.
Задача 12. Комерційний банк отримав кошти у сумі 650 000 грн., а відсоткова ставка обов‘язкових резервів становить 12%. Знайти вільні та обов‘язкові резерви банку від цієї суми.
Після колективного розв’язання цієї задачі доцільно запропонувати аналогічні данні і провести їх обчислення у формі групової роботи: клас розбивається на групи – банки, назви яким вони придумають самостійно. Ставиться вимога обчислити вільні та обов‘язкові резерви їх банку за умов поданих в табл. 2.4.
Таблиця 2.4
Завдання для обчислення резервів банку
| № | Банк | Сума надходжень | Відсоткова ставка обов‘язкових резервів |
| 1. | 20000 | 20% | |
| 2. | 45000 | 12% | |
| 3. | 120000 | 15% | |
| 4. | 22000 | 18% | |
| 5. | S | p % |
Порівнюючи отримані данні, учні роблять висновок, що існує пряма залежність між сумою коштів, які надійшли до банку, та величиною вільних резервів. Як наслідок, кожний банк може видати кредитів не більше за суму його вільних резервів.
Ознайомлення з поняттям обов’язкових резервів банку дає змогу провести дискусію з учнями з питання: "Як Національний банк України впливає на величину кредитів комерційних банків?" В результаті отримаємо відповідь: "Встановленням долі обов‘язкових резервів: чим більше відсоток обов‘язкових резервів, тим менше кредитів може видати банк, і навпаки." Заключним етапом роботи стає виведення загальної формули обчислення обов’язкових та вільних резервів банку, якщо сума вкладу S та відсоткова ставка p % обов‘язкових резервів:
![]() - обов‘язкові
резерви банку, (2.3)
- обов‘язкові
резерви банку, (2.3)
![]() - вільні
резерви банку. (2.4)
- вільні
резерви банку. (2.4)
Після ознайомлення учнів з основними сторонами діяльності банків у державі, доцільно провести дидактичну гру. Для цього клас слід розподілити на п‘ять команд.
Перша – робітники Національного банку; друга, третя, четверта – різні банки; п‘ята – особи, які співпрацюють із банками. Банки варто назвати та описати отриману банківську систему. Отриманий результат слушно відобразити у вигляді схеми (мал. 2.5.).
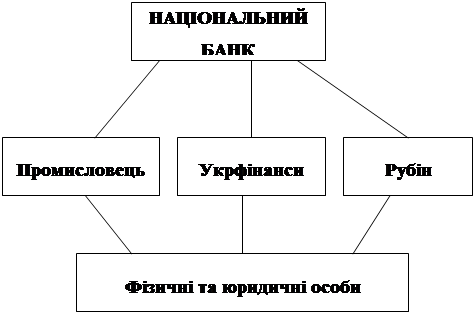
Мал. 2.5. Банківська система на уроці математики
Надалі схему (мал. 2.5) слід доповнити таблицею 2.5.
Завдання на гру.
1. Національний банк встановлює відсоток на обов‘язкові резерви банку, за умови, що кількість обов‘язкових резервів повинна “покривати” половину грошей, які банк бере у фізичних та юридичних осіб на депозитні вклади.
2. Кожна фізична та юридична особа має 3000 гривень. Вони домовляються з одним із банків про депозитний вклад на три роки, а з іншим про кредит на два роки.
3. Кожний банк встановлює власну ставку відсотку на кредит та оформлює договори з фізичними та юридичними особами.
Таблиця 2.5
Початкові данні для виконання завдань
| Банк | Сума в банку | Сума, яка надійшла на депозитні вклади | Відсоткова ставка депозитних вкладів |
| Промисливець | 15000 | 7000 | 16 % |
| Укрфінанси | 17000 | 10000 | 20 % |
| Рубін | 14000 | 5000 | 14 % |
Після оформлення всіх договорів, кожний банк та кожний клієнт банків рахують власний бюджет через три роки.
Національний банк перевіряє обчислення та виносить результати на дошку. Фізичні та юридичні особи, які отримали збитки, шукають варіанти покращення власного стану. Для цього розриваються укладені договори та укладаються нові. Банки, в яких результативна сума буде меншою за початкову, повертають депозитні кошти і надані кредити, а з кожної суми, яка обумовлена договором з клієнтами, виплачує 1 % та починає розрахунки з нової початкової суми.
Діти дуже захоплюються такою діяльністю. Вони набувають нового досвіду у використанні власних коштів при співпраці з банками.
Отже, для розв‘язування математичних задач такого типу цілком досить знань з курсу математики середньої школи. Однак різні поняття та терміни, які зустрічаються в задачах, не є звичними для шкільної програми, тому вимагають додаткового пояснення та обґрунтування. Інколи вони стають зрозумілими вже з тексту задач. Завдяки введенню нових понять розширюються знання учнів та демонструються можливості використання математичних знань у банківській діяльності протягом курсу математики основної школи, що відображено в додатку Є. Це активізує діяльність учнів та збуджує інтерес до практичного застосування шкільних математичних знань.
Ведення задач на діяльність банків до курсу математики основної школи, які пов‘язані з депозитними вкладами та наданням кредитів, ознайомлює учнів із такими фінансовими величинами, як початковий капітал, відсоткова ставка банку, прибуток або відсоткові гроші, термін вкладу або час та результативний капітал. Це показує математичну залежність між ними.
У процесі розв’язування математичних задач на діяльність банків, відбувається усвідомлення учнями таких функцій комерційних банків:
· кредитно-розрахункове обслуговування підприємств, організацій та населення;
· касове обслуговування підприємств, організацій та населення;
· операції з іноземною валютою;
· інші, визначені законодавством.
Задачі на банківські розрахунки, які були використані в ході експерименту, розширили знання учнів про банківську систему України та розкрили деякі її особливості. Ці задачі рівномірно розподіляються за темами шкільного курсу математики, що відображено в додатку А.
2.2. Особливості роботи з задачами на оподаткування
Невід’ємною частиною економічного всеобучу в умовах ринкових відносин України є знання про сплату податків та вміння їх нараховувати.
За допомогою математичних методів, з якими учні знайомляться під час шкільних занять з математики, можна розкрити зміст багатьох податкових термінів, операцій та залежностей, які оточують людину сьогодні. Питання податкових надходжень до бюджету держави та система їх нарахування є однією з фінансових тем, які доцільно було розглянути в ході вивчення математики в основній школі.
У податковій практиці зустрічається велика кількість задач різного типу. Податки – це обов’язкові платежі, які держава стягує із громадян, підприємств та організацій до бюджету. Не всі задачі податкової тематики можуть бути запропоновані до розгляду на уроках математики. Та й не всі мають зв’язок із математикою. Розглянемо лише ті задачі на податки, фабула яких розкриває використання математики в системі податків й ознайомлює із застосуванням математичних понять, операцій та методів у податковій сфері.
Важливо зазначити, що задачі на податки дають можливість реалізувати прикладну спрямованість математики. Вже в основній школі учні вчаться елементам математичного моделювання, знайомляться з особливостями перекладу текстової задачі на мову математики, розкриттям отриманого математичного результату в реальній життєвій ситуації та його аналізом.
У процесі розв’язування математичних задач на податки, учні мають справу з такими поняттями, як платник прибуткового податку, об’єкт оподаткування, сукупний податковий дохід, ставка податку, порядок обчислення і сплата податку, перерахування податку до бюджету, використання податкових коштів державою, тощо. Це формує у них уявлення про шлях сплати податків, розуміння причин їх нарахування. Це допомагає уникнути помилок у життєво важливих питаннях.
Розглянемо конкретне використання таких задач на уроках математики.
Система оподаткування України включає велику кількість різних видів податків. Податкова система – це сукупність установлених у державі податків та механізмів їх сплати.
Для практичного ознайомлення учнів із системою оподаткування в Україні, на різних прикладах та задачах потрібно проілюструвати різні схеми оподаткування. В різних країнах перелік податків включає від 10 до 30 видів. Найпоширенішими є податки на прибуток, на майно (обладнання, будівлі, транспорт і т.д.), на заробітну плату та на спадок.
Узагалі, всі податки за економічним змістом об’єкта оподаткування поділяють за схемою 2.7 [44 , с.234].
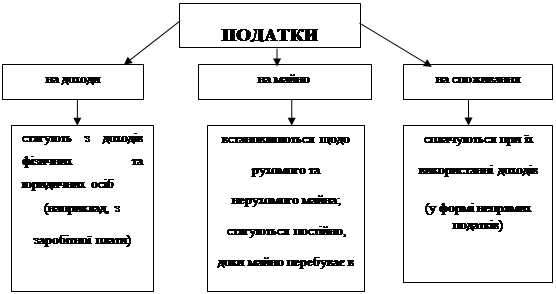
Мал. 2.7. Види податків
Кожний вид податку нараховується у відповідності до законів. Активним учням слід запропонувати самостійно знайти за допомогою комп’ютерних засобів (інтернет) як нараховуються податки на споживання та на майно, на прикладі показати їх дію і зробити доповідь класу. Для зменшення складності завдання доцільно запропонувати декілька сайтів з інтернету звідки можна взяти ці данні.
У дев’ятому класі при повторенні теми “Відсотки” учням може бути запропоновано самостійно на базі витягу з закону “Про прибутковий податок із громадян”, якій діяв до 2004 року обчислити розмір податку з власного сукупного доходу за основним місцем роботи. Таблиця 2.9 може бути продемонстрована учням за допомогою кодоскопа.
Таблиця 2.9
Ставка та розміри прибуткового податку з доходів громадян за місцем основної роботи в Україні (до 2004 року)
|
Місячний сукупний доход, що оподатковується (у неоподатковуваних мінімумах) |
Ставки та розміри податку |
| до 17 грн. включно | не оподатковується |
| від 17 грн. до 85 грн. | 10 % суми, що перевищує 17 грн. |
| від 86 грн. до 170 грн. | 6,8 грн. + 15 % суми, що перевищує доход 85 грн. |
| від 171 грн. до 1020 грн. | 19,55 грн. + 20 % суми, що перевищує доход 170 грн. |
| від 1021 грн. до 1700 грн. | 189,55 грн. + 30 % суми, що перевищує доход 1020 грн. |
| від 1701 грн. і вище | 393,55 грн. + 40 % суми, що перевищує доход 1700 грн. |
Задача 3. Прибутковий податок із сукупного оподаткованого доходу громадян за місцем основної роботи до 2004 року обчислювався за ставками табл. 2.9. [48, с.19]. Обчислити розмір суми податків, яку сплачував кожний член Вашої родини за основним місцем роботи: а) за один місяць; б) за рік.
Розв’язання таких задач в курсі математики знайомить та навчає дітей працювати з витягами законів України.
У дев’ятому класі під час вивчення властивостей арифметичної прогресії учням може бути запропонована наступна задача.
Задача 4. Місячний оподатковуваний дохід за неосновним місцем роботи громадянина в січні становив 450 гривень, а далі збільшувався щомісяця на 20 гривень. Доходи, отримані не за місцем основної роботи, оподатковуються прибутковим податком за ставкою 20 %. Обчислити загальну суму річного податку.
Наведемо можливу методику розв’язування такого типу задач. Спочатку слід звернути увагу учнів на фіксовану ставку податку, тому якби дохід не змінювався, то і сума сплати податку не змінювалась.
Зміни в доходах, які описані в задачі, мають певну математичну закономірність. Учням пропонується перекласти речення задачі "Місячний оподатковуваний дохід за неосновним місцем роботи громадянина в січні становив 450 гривень, і далі збільшувався щомісяця на 20 гривень." на математичну мову. В результаті: "Місячні оподатковувані доходи складають арифметичну прогресію, у якої перший член – 450, а різниця – 20". Таке формулювання налаштовує на виконання певних математичних дій.
Для ілюстрації закономірностей арифметичної прогресії учням пропонується побудувати числову послідовність, яка буде відображати місячний оподатковуваний дохід за неосновним місцем роботи протягом року за умовою задачі.
Далі клас розбивається на дві групи: перша група шукає відповідь за допомогою властивостей вже побудованої прогресії, друга – будує числову послідовність щомісячного податку та за отриманим рядом шукає відповідь.
Наведемо міркування першої групи учнів. В році дванадцять місяців, тому потрібно знайти суму 12 перших членів арифметичної прогресії. Для цього треба обчислити дванадцятий член прогресії (або він вже обчислений на дошці в числовому ряду):
a12 = 450 + (12 - 1) ×20 = 670.
Тоді за формулою суми членів арифметичної прогресії:
![]() - сукупний
річний дохід за неосновним місцем роботи.
- сукупний
річний дохід за неосновним місцем роботи.
Це не є остаточним результатом, тому речення з задачі "Доходи, отримані не за місцем основної роботи, оподатковуються прибутковим податком за ставкою 20 %" також потрібно перекласти на мову математики: "Для обчислення величини податку потрібно знайти 20 % від сукупного річного доходу за неосновним місцем роботи". Тобто:
0,2 × 6 720 = 1 344 (грн.).
Відповідь: сукупний річний дохід за неосновним місцем роботи – 6 720 грн., а податок – 1 344 грн.
Друга група учнів має більше розрахунків, оскільки вони повинні виконати додаткове завдання, яке полягає в побудові числової послідовності податку.
Аналіз результатів показує, що отримані відповіді однакові. Обов’язково потрібно звернути увагу, що допоміжний ряд можна було і не будувати. Достатньо знайти лише його перший та дванадцятий члени.
Виконання такої роботи ознайомлює учнів із деякими фінансовими розрахунками, які проводить кожний громадянин України при заповненні податкової декларації.
Для ознайомлення учнів із сучасною системою оподаткування, учням у дев’ятому класі при вивченні теми "Властивості функцій" пропонується завдання: "На сайті Верховної ради України (www.rada.gov.ua) знайти, як нараховується прибутковий податок з доходів громадян за основним місцем роботи з 2004 року та як він нараховувався до 2004 року. Скласти відповідні функції у = у(х), де х – місячний сукупний дохід, у – величина прибуткового податку. Побудувати графіки. Провести порівняльний аналіз графіка до 2004 року та графіка після 2004 року. Яке оподаткування діє сьогодні: прогресивне, пропорційне чи регресивне?"
Для наочної демонстрації різних податкових ставок у дев’ятому класі під час вивчення теми “Нерівності” в ході педагогічного експерименту була використана така задача.
Задача 6. Якщо місячний оподатковуваний дохід становить від 1021 до 1700 гривень, то прибутковий податок за основним місцем роботи обчислюється за формулою 189,55 + (х - 1020)×0,3, а за неосновним місцем роботи - за формулою 0,2х, де х - місячний дохід, що підлягає оподаткуванню. Який повинен бути місячний оподатковуваний дохід, щоб податок за основним місцем роботи був менше за податок за неосновним місцем роботи?
Пропонуємо методику розв’язання задач даного типу. Колективний аналіз задачі підводить учнів до висновку, що для знаходження відповіді необхідно розв’язати нерівність:
189,55 + (х - 1020)×0,3 < 0,2x.
В результаті:
x < 1164,5.
Для знаходження остаточної відповіді необхідно звернути увагу учнів на обмеження, які накладені в умові задачі на місячний оподатковуваний дохід. Тому отримаємо, що для умови задачі х Î [1021; 1164,5). При перекладі математичного результату на фінансову мову відповідь формулюється наступним чином: місячний оподатковуваний дохід може бути більше або дорівнювати 1 021 грн., але менше за 1 164,5 грн.
Для повного аналізу цього факту учням пропонується самостійно порівняти розміри податку за основним та неосновним місцем роботи у всіх інших сумах місячного оподатковуваного доходу.
Для самостійної роботи учням можна запропонувати провести порівняльний аналіз розміру податку за основним місцем роботи, який обчислюється за таблицею 2.8, та розміром податку в 13 % від місячного оподатковуваного доходу, який нараховується в Україні з 2004 року. Знайти при якому місячному оподатковуваному доході розмір податку збільшиться, а при якому зменшиться?
Така робота навчає аналізувати чинні закони України та привчає самостійно рахувати суму сплачених податків.
Ознайомлення учнів з податковою системою України потребує звернути їх увагу на такі запитання: для чого нараховуються податки в державі? як використовуються отримані податкові кошти державою? Відповіді на ці запитання доцільно проілюструвати за допомогою навчальних задач, приклади яких наведені в додатку Б. Зокрема:
Задача 7. З усіх доходів Держави податкові надходження в 1999 році становили 76,5%, що становить 25 130 млн. грн. Які видатки бюджету України в 1999 році, якщо вони перевищили доходи на 1 944,5 млн. грн.?
Ця задача може бути запропонована в 9 класі при вивченні теми “Відсоткові розрахунки”.
Податки в Україні розподіляються за окремими галузями. Наведемо приклади задач, які розкривали це питання в ході педагогічного експерименту.
1. Освіта та охорона здоров’я.
Задача 8. Видатки на освіту та охорону здоров’я разом за 1998 рік становлять 8 196,2 млн. грн., при чому на освіту виділено з Державного бюджету на 932,2 млн. грн. більше. Знайти скільки на освіту, а скільки на охорону здоров’я виділено на кожного громадянина України, якщо населення України 42 млн.
Задача 9. В Україні частка видатків на охорону здоров’я, відповідно до закону про державний бюджет на 1998 рік, складала 11 % всіх державних видатків і становила приблизно 75 гривень на одного громадянина на рік. Обчислити наближено (з точністю до млн.) кількість коштів у державному бюджеті на 1998 рік, якщо кількість населення України становила 42 млн.
2. Соціальна допомога.
Задача 10. В Україні в 1999 році на соціальну допомогу було використано 4 147,1 млн. грн. із Державного бюджету. Серед цих коштів 74% отримано за допомогою різних видів податків. Яка кількість коштів була використана державою на допомогу безробітним та малозабезпеченим, якщо вона становила 0,001 % від коштів, спрямованих на соціальну допомогу за рахунок податків?
3. Пенсії.
Задача 11. Яку кількість грошей держава повинна виділити для надання пенсій в країні за умови табл. 2.12. [55,c.231]
Таблиця 2.12
Надання грошової допомоги непрацездатним громадянам
| Види пенсій | Кількість громадян, тис. | Середній розмір допомоги, грн. |
| за віком | 1366 | 22,5 |
| за інвалідністю | 374,2 | 20,9 |
| у разі втрати годувальника | 540,4 | 22,6 |
| за вислугу років | 2,5 | 9,6 |
| соціальна пенсія | 391,3 | 30,5 |
| Всього |
Отже, податкові надходження держави в основному розподіляються на освіту, на охорону здоров’я, на соціальну допомогу, пенсії громадян та інші важливі галузі життя. Такі задачі можуть бути використані вчителями в процесі вивчення математики на будь-якому етапі роботи.
В ході проведеного нами експерименту було виявлено, що найбільша складність при роботі із задачами на податки виникає при переведенні фінансової мови задачі на математичну та при виведені фінансового значення математично отриманого результату. Для усунення цієї проблеми було складено словник фінансових термінів. Він показував тлумачення фінансової термінології та математичних законів, з якими вони пов’язані (додаток К). Учні самостійно його доповнювали та знаходили математичні зв’язки між фінансовими термінами, які розглядались раніше. В ході вивчення математики в основній школі відбувалось поступове ознайомлення учнів з податковою системою України (див. додаток Є).
Ознайомлення учнів із системою обчислення податків та їх використання державою є важливим елементом загальної підготовки майбутнього громадянина України для життя в умовах ринкової економіки. Відображення в задачах реальних податкових даних нашої держави та інших держав спрямовують учнів на пошук величин за допомогою засобів комп'ютеризації. На уроках математики, працюючи з податковими даними, учні усвідомлюють необхідність сплати податків, розуміють систему їх нарахування та подальше використання податкових надходжень Державою. Такі задачі можуть використовуватись у процесі вивчення тем шкільного курсу математики (додаток Б).
2.3 Mісце задач на цінні папери в курсі математики основної школи
Ринок – це обмін товарами. Головним еквівалентом товару виступають гроші. З тих пір, як гроші були введені як засіб обміну товарів, вони виступають як новий товар, який поклав основу для створення фінансового ринку. Це вторинний ринок, де товаром виступають благородні метали, гроші, валюта та цінні папери. Торгівля цінними паперами відбувається на первинному та вторинному ринку цінних паперів.
Ознайомлення з ринком цінних паперів та його особливостями можливо провести, якщо на уроках математики включати роботу з задачами про різні види цінних паперів. Так, наприклад, під час вивчення теми “Розв’язування задач за допомогою рівнянь” у дев’ятому класі в ході експерименту була запропонована така задача.
Задача 1. У 1996 році ринок цінних паперів України мав вартість 1994,6 млн. грн. На ньому акції складали на 204,8 млн. грн. більше, ніж векселя, та на 691,4 млн. грн. більше за облігації. Інші цінні папери мали вартість 624,9 млн. грн. Знайти яка вартість облігацій, акцій та векселів окремо на ринку цінних паперів в 1996 році.
Спочатку учні були ознайомлені із зв’язком ринку цінних паперів із ринком грошей та з ринком капіталів. Тут відбувається купівля-продаж цінних паперів. Цінний папір є свідоцтвом про право власності на капітал. Він відображає відношення позики та дає право на отримання певного прибутку, будучи елементом фінансового ринку. Ознайомлення учнів з цими фактами є важливим етапом при роботі з такими задачами, оскільки учні повинні розуміти не лише математичний зміст задачі, а також і її фінансове значення та застосування.
Також важливо показати учням, що фінансовий ринок складається з грошового ринку та ринку капіталів. Його структура (мал. 2.9.) може бути проілюстрована за допомогою кодоскопа при першому ознайомленні з цінними паперами для розуміння місця цінних паперів у фінансовому колі питань. На грошовому ринку обертаються засоби, які виступають короткостроковими фінансовими коштами. Ринок капіталів – це ринок середньо - та довгострокових накопичень. Межа між ними дуже умовна, бо між цими ринками постійно відбувається перебіг коштів.
|
|
Мал. 2.9. Схема фінансового ринку
Особливістю первинного ринку є надходження грошей покупців цінних паперів прямо до підприємства, яке випустило цінні папери. Вторинний ринок функціонує для обігу раніше випущених цінних паперів, тобто їх купівлі-продажу. Купити цінні папери можна у торговця, через мережу Державної акціонерної компанії "Національна мережа аукціонних центрів" чи у приватної особи. Продати цінні папери можна будь-якій фізичній або юридичній особі, яка хоче їх купити.
Коли учні усвідомили факти, які проілюстровані в задачі, для подальшого розв’язування учням пропонується перекласти фінансові дані задачі на математичну мову, використовуючи відповідні математичні терміни, які розкривають математичну залежність між елементами ринку цінних паперів. Така робота з реальними даними держави, а також із відповідальними елементами фінансового ринку рідної країни активізує пізнавальну діяльність учнів, виховує уважність, повагу до математичних законів й операцій в цілому та показує використання математичних знань в реальних умовах.
Міркування учнів, приводять до висновку, що за х млн. грн. доцільно позначити вартість всіх акцій на ринку цінних паперів України в 1996 році. Тоді (х - 204,8) млн. грн. – вартість всіх векселів, а (х - 691,4) млн. грн. - вартість всіх облігацій. Враховуючи, факт, ринок ціних паперів включає акції, облігації, векселя та інші види цінних паперів, складається вираз для обчислення вартості ринку цінних паперів в 1996 році:
(х + (х - 204,8) + (х - 691,4) + 624,9) млн. грн.,
значення якого дорівнює 1 994,6 млн. грн.
Отримали рівняння:
х + (х - 204,8) + (х - 691,4) + 624,9 = 1 994,6,
розв’язування якого дає відповідь: х = 755,3 (млн. грн.) - вартість всіх акцій.
Тоді учні самостійно шукають відповідь на запитання задачі, враховуючи математичні закономірності між вже відомими фінансовими даними, та тими, що необхідно відшукати. Отримують, що вартість акцій -755,3 млн. грн., вартість облігацій – 63,9 млн. грн., а вартість векселів – 550,5 млн. грн.
Така робота ілюструє учням значення ринку цінних паперів у фінансовому колі держави, показує його різноманітність та багатоаспектність. Доцільно зазначити, що українським законодавством визначені такі види цінних паперів:
а) акції;
б) облігації внутрішніх республіканських і місцевих позик;
в) облігації підприємств;
г) казначейські зобов'язання підприємств;
д) ощадні сертифікати;
е) векселі;
є) приватизаційні папери;
ж) інвестиційні сертифікати.
Серед перерахованих цінних паперів, у нашому дослідженні ми виділили три види, які можна та доцільно використовувати в курсі математики основної школи. Це акція, облігація та вексель.
Найпростіші фінансові обчислення на ринку цінних паперів можуть бути проілюстровані при розв’язуванні задач на вексель.
При розв’язуванні задач на вексель треба звернути увагу на те, що розрізняють прості та переказні векселі.
Простий вексель свідчить про таке: векселедавець (емітент, той, хто цей вексель написав) дає чесне слово сплатити обумовлену суму коштів в обумовлений строк тому, хто цей вексель пред'явить. Чесне слово векселедавця може бути (бажано, щоб саме так і було) підтверджене іншою особою, як правило, - це банк або фірма, фінансовий стан якої не викликає сумнівів.
Переказний вексель - це наказ векселедавця іншій особі заплатити власнику векселя обумовлену суму в обумовлений термін. Щоб власник векселя міг ним скористатися, переказний вексель має бути акцептований, тобто особа, якій було наказано заплатити, має підтвердити свою згоду це зробити. У цьому випадку саме вона дає чесне слово сплатити за векселем. Не зайвим було б підтвердження банком або іншою фірмою, якій власник векселя довіряє.
При роботі з векселями потрібно враховувати, що:
1. При позиках кредитор найчастіше отримує відсоток наперед.
2. Кредитор не може вимагати виплати грошей раніше терміну, вказаного в векселі.
3. В строк, визначений у векселі, кредитор отримує з векселем вказану у ньому суму.
Процес знаходження теперішньої вартості майбутнього платежу називається дисконтування. Дисконтувати вексель – це знайти суму грошей, отриману продавцем векселю. Цю суму називають ціною векселя.
Задача 2. Наведений вище вексель (мал.2.10) Чіп продає банку 19 вересня 2003 року з дисконтом (знижкою) за річною ставкою 10 %. За якою ціною купить банк цей вексель?
Перед розв’язанням проводиться фронтальна бесіда в ході якої учні усвідомлюють, що на момент продажу векселя до терміну погашення залишилось 3 місяця. Ставка 10 % є річною, тобто ставка за 12 місяців. Ці данні показують, що необхідно знайти відсоткову ставку за три місяця. Як? Міркування учнів приводять до того, що за 3 місяця відсотки становлять (10×3) / 12 = 2,5 %.
Для знаходження дисконту необхідно від фактичної вартості векселя знайти ці відсотки. Отже, знайдемо суму грошей, яка утримується з валюти векселя при його продажу, тобто дисконт: 4 600 × 0,025 = 115 (грн.)
Тоді банк купить цей вексель за 4 600 – 115 = 4 485 ( грн.)
Отже, 4 600 грн. – фактична вартість векселя;
2,5 % - термінові відсотки;
115 грн. – дисконт;
4 485 грн. – ціна векселя на 19 вересня 2003 року за ставкою 10 % річних.
Після цього учням пропонується знайти всі ці величини для отриманих векселів (з якими вони працювали раніше) на сьогоднішній день при знижці за 12% річних. Проблемні ситуації виникнуть при розрахунку термінових відсотків у випадку, коли термін потрібно обчислювати з точністю до дня. Це активізує діяльність учнів та потребує деяких самостійних міркувань у розв’язання ситуації. Таке завдання може бути запропоноване учням, які цікавляться математикою, та мають відповідні вміння роботи з фінансовими величинами. Доцільно також надати учням відповідні фінансово-математичні теми для виконання реферативної роботи.
Отже, при роботі з векселями необхідно розрізняти такі величини:
· дата погашення векселя,
· сума погашення векселя (валюта векселя),
· ставка відсотка,
· ціна векселя (сума, отримана від продажу векселя),
· час роботи з векселем (залишок до терміну погашення).
Наступним цінним папером для ознайомлення учнів є акція. Акція – це цінний папір, якій випускається фірмами з метою залучення капіталу та надає право її власнику на отримання прибутку акціонерного товариства у вигляді дивідендів, на участь в управлінні акціонерним товариством та на частину товару, який залишається після її ліквідації. Вона підтверджує дольову участь у статутному фонді акціонерного товариства. Акція не має встановленого строку обігу. Якщо ви купили акцію, то це означає, що ви стали акціонером і співвласником підприємства. Ви маєте право брати участь у загальних зборах акціонерів та голосувати, обирати правління, ревізійну комісію та отримувати дохід у вигляді дивідендів, якщо за звітний період підприємство має прибуток. Рішення про виплату дивідендів та їх розмір приймає правління, а затверджують загальні збори акціонерів - вищий орган управління акціонерним товариством. Крім того, у випадку ліквідації акціонерного товариства (підприємства) ви можете претендувати на долю його майна, пропорційну вартості вашим акціям після розрахунку товариства з державою, кредиторами та найманими працівниками. Всі ці факти повинні бути включені у первинне ознайомлення учнів з акцією.
Статутний капітал акціонерного товариства розподілено на певну кількість акцій, які мають номінальну вартість. Номінальна вартість акції – це її вартість, за яку вона була вперше продана. Тут відбувається обчислення за формулою, яка демонструється учням за допомогою кодоскопа та залишається на дошці доки виконується завдання:
![]() , де (2.5)
, де (2.5)
K - статутний капітал;
H0 - номінальна вартість звичайної акції;
N0 – кількість звичайних акцій;
Hi - номінальна вартість привілейованої акції;
Ni - кількість привілейованих акцій.
Для ілюстрації такого розподілу установчого капіталу учням пропонується заповнити порожні клітинки в табл. 2.13.
Таблиця 2.13
Розподіл установчого капіталу на акції
| K |
H0 |
N0 |
H1 |
N1 |
H2 |
N2 |
H3 |
N3 |
| 150 | 5 | 50 | 100 | 65 | 125 | 84 | 250 | |
| 330860 | 127 | 18 | 54 | 45 | 72 | 404 | 700 | |
| 32960 | 160 | 100 | 74 | 80 | 52 | 67 | 200 |
Перед початком роботи обов‘язково необхідно звернути увагу учнів на наявність різних видів акцій:
1. Прості акції дають право голосу на загальних зборах акціонерів і, таким чином, право на участь в управлінні підприємством.
2. Привілейовані акції дають власникові переважне право на отримання дивідендів, а також на пріоритетну участь у розподілі майна акціонерного товариства у разі його ліквідації. Власники привілейованих акцій не мають права брати участь в управлінні товариством, якщо інше не передбачено його статутом. Привілейовані акції бувають різних видів, і, відповідно, мають різну вартість та різну кількість. І прості, і привілейовані акції можуть бути іменними і на пред'явника.
3. Іменні акції містять інформацію про акціонера. Коли акції продаються і купуються, ця інформація змінюється.
4. Акції на пред'явника не містять інформації про їх власника.
Для заповнення другого та третього рядка таблиці доцільно учням запропонувати скласти вираз для обчислення установчого капіталу у якому невідому величину позначити відповідною буквою. Для заповнення таблиці учням пропонується скласти рівняння. Перша група заповнює другий рядок, а друга – третій. Аналіз отриманих результатів проводиться колективно.
Крім номінальної вартості, акція має ще й ринкову вартість, або курс акції, - ціну, за якою вона може бути проданою на даний момент. Курс акції залежить від дивідендів, які отримує власник. Для простеження цієї залежності можна розглянути таку задачу.
Задача 4. Підприємство видало 15 звичайних акцій вартістю 350 гривень кожна. Виплачені дивіденди цих акцій у 2003 році становили 600 грн., а в 2004 році – 3000 грн. Який прогнозований курс цих акцій можливий у 2005 році?
Робота над цією задачею потребує розуміння зв’язку вартості акції з дивідендами. Міркування учнів можливо спрямувати за наступною схемою.
Так як на виплату дивідендів за всіма акціями в 2003 році було спрямовано 1 300 грн., то виплата на одну акцію становила
600 : 15 = 40 (грн.),
тобто ринкова вартість акції в 2003 році вже була не менше за
350 + 40 =390 (грн.).
Аналогічно, в 2004 році курс цих акцій вже становив не менше за
390 + (3 000 : 15) = 590( грн.).
Тому на 2005 рік прогнозується курс акцій не менше 590 гривень.
Необхідною умовою зростання курсу акцій є стабільна робота підприємства, та, як наслідок, зростання ринкової вартість курсу акцій. Зниження економічного потенціалу виробництва тягне за собою зменшення виплати дивідендів, зниження курсу акції до номінальної вартості, а за деяких умов і визначення ринкового курсу, нижче номінальної вартості. Робиться висновок: чим вище курс акції, тим вищий рівень доходів (дивідендів) можливо отримати на ринку цінних паперів від фінансових операцій з акцією.
Отже, акція має номінальну вартість, яка встановлюється при створенні акціонерного товариства і фіксується на бланку акції, та курсову (ринкову) вартість, яка зумовлюється попитом і пропозицією на ринку цінних паперів та прибутку від діяльності підприємства, тобто поточна ціна акцій на фондовій біржі чи в позабіржовому обігові.
В Україні дуже часто використовується видання привілейованих акцій, розмір дивідендів яких не фіксований, а визначається за формулою:
![]() , де (2.6)
, де (2.6)
D – дивіденд,
n – чистий прибуток підприємства,
K – статутний капітал.
Щоб робота учнів носила більш практичний характер доцільно запропонувати учням вивести з формули як знаходяться установчий капітал та чистий прибуток підприємства. Далі учні розподіляються на дві групи і складають задачі, обернені до даної, після чого кожен учень самостійно розв’язує отримані задачі. Ця робота показує учням як розвиток діяльності підприємств у нашій державі пов’язаний з підвищенням доходів власного бюджету кожного громадянина.
Під час вивчення теми “Нерівності” корисно розглянути таку задачу.
Задача 6. Який чистий прибуток повинно отримати підприємство, щоб дивіденд привілейованих акцій цього підприємства був не менше за 0,8 %, якщо статутний капітал становить 456 000 гривень?
Серед висновків до цієї роботи, обов‘язково треба звернути увагу на зв‘язок прибутку підприємства, дивіденду акцій та попитом на ці акції.
Придбання акції означає придбання частини даного підприємства. Це дає можливість взяти участь в управлінні його діяльністю та отриманні прибутку у випадку успішної роботи підприємства.
У дев‘ятому класі програма з математики передбачає вивчення розділу "Елементи прикладної математики", який дає можливість використання різних фінансово-математичних задач різного характеру для демонстрації фінансового застосування математики. Саме тут цікаво розглянути задачу такого змісту:
Задача 7. Ви маєте суму 1000 гривень, яку бажаєте розмістити з метою отримання як найбільшого доходу. Банк залучає кошти клієнтів на депозитні вклади під 8 % річних. Акціонерне товариство випустило цінні папері у вигляді 8 привілейованих акцій номінальною вартістю 250 гривень із виплатою дивідендів у розмірі 10 %, та 10 звичайних акцій номінальною вартістю 200 гривень. На виплату дивідендів акціонерним товариством виділено 800 гривень. Куди краще вкласти гроші: а) у банк; б) у привілейовані акції; в) у звичайні акції?
Розв‘язання задачі можна провести в такому вигляді. Для пошуку відповіді учні розділяються на три команди, кожна з яких рахує дохід від відповідного вкладу. Результати команди оголошують:
1-ша команда: Якщо внести гроші на депозитний рахунок у банк, то за рік можна отримати 80 гривень у вигляді нарахованих та виплачених банком доходів.
2-га команда: На привілейовані акції виплачені дивіденди складуть 8×10% = 80% від суми виділеної на дивіденди, тобто 640 грн. Одна привілейована акція дає в рік дохід 640 : 8 = 80 (грн.)
Розрахунок показує, що можна купити (1000 грн. : 250 грн.) = 4 привілейовані акції та отримати за рік 4×80 = 320 (грн.) прибутку у вигляді виплачених дивідендів.
3-а команда: На виплати по звичайних акціях залишиться 800 - 640 = 160 грн. А виплачені дивіденди на одну звичайну акцію становлять
160 : 10 = 16 (грн.)
Можна придбати 1000 : 200 = 5 звичайних акцій та отримати за них
5 × 16 = 80 (грн.)
Колективно здійснивши порівняльний аналіз отриманих результатів, маємо відповідь: найбільшій прибуток буде отримано у разі придбання привілейованих акцій акціонерного товариства.
Також при розгляді особливостей акції учням може бути запропонована така задача.
Задача 3. Як отримати збільшення капіталу, якщо відомо, що акція в Нью-Йорку продається за ціною 200 $, а в Лондоні – за ціною 100 фунтів, а поточний обмінний курс долара по відношенню до фунта 1,71?
Проблемна ситуація полягає в тому, що для розв’язання задачі не вистачає початкових даних. Тому в цьому випадку можливий наступний ланцюг дій: взяти в борг 100фунтів, купити акцію в Лондоні за 100 фунтів, продати її в Нью-Йорку за 200 доларів, обміняти 200 доларів за курсом 1,71 на 116,9 фунтів, повернути борг 100фунтів. У результаті отримаємо чистий прибуток 16,9 фунтів. Така ілюстрація ознайомлює учнів із можливістю арбітражних стратегій.
Отже, у курсі математики основної школи через розв’язання навчальних задач можна ознайомили учнів з такими особливостями акцій, як:
· особливості обчислень при роботі з простими та привілейованими акціями;
· вплив діяльності підприємства на ринкову вартість акції;
· зв’язок розвитку підприємницької діяльності з сімейним бюджетом громадян через акції;
· арбітражні стратегії та інше.
Наступний цінний папір, з яким важливе ознайомлення учнів, - облігація. Облігація - цінний папір, якій задовольняє внесок її власника грошових засобів та підтверджує зобов‘язання емітента повернути інвестору номінальну вартість цього паперу в певний термін із виплатою зафіксованого в ньому відсотку від номінальної вартості. Облігації видаються для отримання грошей у борг підприємством.
Таким чином, облігації підтверджують наявність кредиторсько-дебіторських взаємовідносин між емітентом і власником облігацій. В цьому випадку власник облігації надає кошти, а емітент отримує їх в користування. Випускаючи облігації, емітент тим самим офіційно оголошує про свою потребу в позикових коштах, про терміни, протягом яких ці кошти йому знадобляться та про розмір винагороди, яку він згоден платити за можливість користуватися грошима. У більшості випадків необхідним є повідомлення про цілі, для досягнення яких йому ці кошти потрібні, про свою готовність у майбутньому повністю повернути борг.
Прикладом можуть бути облігації державного займу. Дуже близькими за своєю суттю до облігацій є казначейські зобов'язання України та ощадні сертифікати, які емітують банки.
Облігації відрізняються від акцій головним чином тим, що їх власник не є членом акціонерного товариства та не має майнових прав або права голосу на зборах акціонерів.
Учням варто пояснити, що як і акції, облігації можуть бути іменними та на пред’явника, знаходитися у вільному обігові та з обмеженнями. Крім того, розрізняють процентні та безпроцентні (цільові) облігації. Прибуток із процентних облігацій виплачується відповідно до умов їхнього випуску, якими передбачаються фіксовані розміри та строки виплати процентів. Номінальна вартість облігації повертається власникові після її погашення. Прибуток із облігацій цільових позик (безпроцентних) не виплачується. Власник такої облігації після настання обумовленого терміну має можливість придбати відповідні товари.
Далі учням можна запропонувати розв’язати самостійно наступну задачу.
Задача 9. Уявіть, що ви директор фабрики, яка виготовляє трикотажні вироби трьох видів. Для Вашої подальшої роботи необхідно отримати кредит на 5 млн. грн. Ви випускаєте облігації вартістю 1000 грн. Яку кількість товару та за якою вартістю ви повинні випустити, щоб власники облігацій могли через рік придбати товари на отримані облігації а ви отримали прибуток, якщо кожний виріб першого виду має вартість 520 грн., другого – 730 грн., а третього – 380 грн.?
Така задача навчає дітей раціонально розподіляти отримані кошти.
Характеристиками облігації є час погашення, вартість погашення та виплата до погашення.
Як і акції, облігації мають ринкову вартість.
Якщо облігація, яка отримана в момент випуску, зберігається в інвестора до терміну погашення, то він отримає прибуток. Але якщо інвестор з деяких причин продасть її до терміну погашення, то рівень доходності облігації буде залежати від її ринкової вартості на момент продажу. Для ілюстрації пропонується задача.
Задача 10. Інвестор отримав облігацію номінальної вартості 3 200 грн. з терміном погашення 3 роки та відсотковою ставкою 10 % річних. Який прибуток отримає інвестор:
а) через три роки?
б) якщо через рік він продасть її за ринковою вартістю 3 750 грн.?
Яка з проведених операцій (залишити облігації у себе або продати) дасть кращий фінансовий результат?
Розв‘язування задачі можна провести, якщо учнів розподілити на дві команди: перша команда – шукає відповідь на запитання а), а друга – на б). Учні по групах обговорюють данні задачі та приходять до висновків:
а) Спочатку треба обчислити, який прибуток має інвестор щорічно:
3 200 × 0,1 = 320 (грн.)
через три роки прибуток інвестора становитиме:
320 × 3 = 960 (грн.)
б) якщо облігація буде продана, то прибуток отримаємо за правилом:
(3 750 +320) – 3 200 = 870 (грн.)
В даному випадку потрібно проаналізувати отримані данні, та звернути увагу учнів на термін отримання реального прибутку. Прибуток на 960 грн. буде отриманий лише через три роки, а на 870 грн. – вже через один рік. Це є реальні гроші, якими можна розпоряджатися на власний розсуд чи знову включати в оборот заради нового прибутку, а не боргове зобов’язання з терміном погашення лише через 2 роки. Тому цікаво дати учням завдання самостійно знайти такий шлях використання отриманих грошей протягом наступний двох років, щоб за цей термін інвестор міг отримати ще більший прибуток, ніж попередній.
Це завдання навчає дітей знаходити різні шляхи збільшення доходів та порівнювати результати від використання коштів.
Таким чином, для роботи з облігаціями учнів потрібно ознайомити з математичною залежністю між такими величинами, як номінальна вартість облігації, ринкова вартість облігації, строк погашення облігації, відсоткова ставка облігації, прибуток з облігації та вартість погашення облігації. Вже в дев’ятому класі при вивченні теми “Елементи прикладної математики” учні можуть віднайти такі формули:
![]() , (2.7)
, (2.7)
![]() , (2.8)
, (2.8)
![]() або
або ![]() , (2.9)
, (2.9)
де W - вартість погашення облігації,
Р – прибуток з облігації,
R - ринкова вартість облігації,
N – номінальна вартість облігації,
p – строк від початку дії облігації,
v – відсоткова ставка.
Ознайомлення з ринком цінних паперів є необхідним елементом сьогоднішньої освіти в Україні, бо ринкові відносини в державі набувають все більших обертів. Цінні папери стають невід’ємної ланкою розвитку фінансового ринку країни.
Для ілюстрації важливості ринку цінних паперів в Україні під час вивчення теми “Графіки функцій та їх властивості” пропонується побудувати графіки розвитку ринку цінних паперів та видів цінних паперів за даними таблиці 2.15.
Таблиця 2.15
Вартість цінних паперів, млн. грн. [55, c.81]
| 1996 | 1997 | 1998 | 1999 | 2000 | |
| Всього | 1994,6 | 5103,8 | 12320,0 | 21909,8 | 34406,2 |
| Акції | 755,3 | 2814,7 | 8908,3 | 15010,9 | 21610,9 |
| Облігації | 63,9 | 612,2 | 1248,1 | 1020,8 | 771,9 |
| Векселі | 550,5 | 780,4 | 1359,2 | 4704,2 | 9800,8 |
| Інші |
Обов’язково потрібно провести аналіз отриманих графіків та звернути увагу учнів на високі темпи розвитку ринку цінних паперів у державі.
Отже, в процесі навчання використання математичних задач про цінні папери розширює клас учбових задач. Ці задачі протягом вивчення курсу математики в основній школі ознайомлюють учнів з важливими фінансовими поняттями, які використовуються в роботі з цінними паперами (додаток Є). Це надає більше можливостей для розвитку творчості дитини та ілюстрації математичних законів на реальних об’єктах, які займають важливе місце в суспільних умовах ринкової економіки.
При розв’язування математичних задач про векселі учні знайомляться з такими величинами, як дата погашення векселя, сума погашення векселя (валюта векселя), ставка відсотка, ціна векселя (сума, отримана від продажу векселя) та час роботи з векселем (залишок до строку погашення) й вчаться знаходити математичні залежності між ними.
Математичні задачі про акцію як цінний папір знайомлять учнів у процесі роботи з номінальною вартістю акції, яка встановлюється при створенні акціонерного товариства і фіксується на бланку акції чи курсовою (ринковою) вартістю акцій Це зумовлюється попитом і пропозицією на ринку цінних паперів та правилами знаходження прибутку від діяльності підприємства, тобто поточною ціною акцій на фондовій біржі чи в позабіржовому обігові. Задачі про акції відображають вплив фінансового стану підприємства та держави на такі характеристики акції.
Фабула учбової математичної задачі про облігацію на ринку цінних паперів показує зв’язки між номінальною вартістю облігації, ринковою вартістю облігації, строком погашення облігації, відсотковою ставкою облігації, прибутку з облігації, вартістю погашення облігації, які можуть відображатись за допомогою формул (2.7)- (2.9).
Всі зазначені види цінних паперів характеризуються величинами, між якими діють математичні залежності, доступні для розгляду в курсі математики основної школи (додаток В).
2.4. Методичні рекомендації використання задач на сімейний бюджет
Кожна сім’я для підвищення свого добробуту застосовує основний принцип бюджетного формування - планування та прогнозування власних доходів і витрат. Збалансований підхід до формування сімейного бюджету дозволяє родині досягнути вищого рівня життя та дещо заощадити. На її бюджет впливають різні чинники, врахування яких дозволяє досягнути оптимального співвідношення між доходами та витратами. Ці факти можна продемонструвати учням через математичні задачі фінансового змісту.
Доходи сімейного бюджету формуються по-різному. Вони залежать від соціально-економічного статусу родини, кількості членів родини та кількості працюючих осіб. Для деяких родин основним джерелом доходу виступає заробітна плата, для інших – доходи від підприємницької діяльності, а в сільськогосподарській місцевості – доходи від особистого господарства. Також поповнення доходів родини можливе за рахунок надання власних приміщень в оренду, отримання дивідендів, спадщини та інших надходжень. Кожна родина має реальне збільшення власного доходу за рахунок отримання законодавчо визначених соціальних гарантій: отримання пенсій, стипендій, надання одноразових виплат у випадку народження дитини, втрати годувальника тощо.
Витрати сімейного бюджету залежать від досягнутого життєвого рівня. Вони включають витрати на придбання продуктів харчування, одягу, взуття, предметів особистої гігієни, придбання житла та його утримання, предмети тривалого користування, власний духовний та культурний розвиток, сезонні закупки, оплату відпочинку, оплату проїзду, платні послуги, різні внески, тощо.
В Україні на законодавчому рівні держава забезпечує громадян безкоштовною освітою, безкоштовним медичним обслуговуванням. Родина також має можливість в разі необхідності отримувати різні пільги. Проте, як альтернатива, родина, в залежності від рівня доходів, може коригувати витрати для отримання освіти та медичного обслуговування підвищеного рівня. Крім цього, необхідно враховувати, що “кожен зобов'язаний сплачувати податки і збори в порядку і розмірах, встановлених законом [32,ст.67]", тобто сплата податків є важливою статтею витрат сімейного бюджету.
Розумне планування доходів та витрат дозволяє родині заощаджувати власні кошти та спрямовувати їх на підвищення свого добробуту. Тому важливо, серед багатьох аспектів проблеми формування підготовки учнів до дорослого життя, наголосити на розумінні формування сімейного бюджету. Для розв’язання цієї проблеми слід розглянути математичні задачі, які розкривають це питання. Вони охоплюють велике коло фінансових операцій.
Бюджет кожної сім'ї є важливою складовою фінансової системи будь-якої країни. Визначимо це поняття. Згідно словника іншомовних слів "бюджет" - це розпис грошових доходів та видатків держави, підприємства чи установи на певний період" або "сукупність доходів і видатків особи, сім’ї за певний період". Розглядаючи бюджет як економічну категорію, відразу видно, що бюджет родини є складовою частиною загального поняття "бюджет".
Для ознайомлення учнів із питаннями бюджету родини, вчитель повинен, в першу чергу, пояснити особливості його формування, а потім визначити, які статті доходів та видатків мають сім’ї нашої країни.
На уроках математики під час вивчення теми “Нерівності” може бути запропоноване таке завдання:
Задача 2. Дохід від заробітної плати в родині у 1999 році складав 450 гривень на місяць. Заробітна плата батька відноситься до заробітної плати мати як 3 : 2. Знайти в яких галузях економіки працюють батьки, використовуючи данні наведені в табл. 2.16.
Таблиця 2.16
Середня заробітна плата в Україні в 1999 році
| Середня заробітна плата, грн. | |
|
сільське господарство торгівля будівництво промисловість зв’язок річковий транспорт |
100,0 180,0 211,0 217,0 260,0 270,0 |
При розв’язуванні цієї задачі розглядаються два випадки:
а) заробітну плату в родині отримують лише батьки.
Тоді задача розв’язується складанням лінійного рівняння
3х + 2х = 450.
б) дохід родини від заробітної плати залежить не лише від зарплати батька та матері (є ще хтось хто отримує заробітну плату, наприклад, син).
У цьому випадку для відшукання відповіді розглядається нерівність
3х + 2х < 450.
Розв’язування отриманого рівняння та нерівності приводить до відповіді. Доцільно учням запропонувати відшукати дані про середню заробітну плату у попередньому році в Україні та спробувати скласти задачу відповідну до наведеної вище провести порівняльний аналіз зміни заробітної плати в різних галузях економіки.
Подальші міркування узагальнюють, що занижена заробітна плата обумовлює низькі грошові доходи населення, які в свою чергу призводять до скорочення платоспроможного попиту.
У структурі доходів української сім'ї за останній час зросли надходження від особистих господарств. Дохід від особистого господарства передбачає надходження в натуральній формі та його перерахування в грошовий еквівалент. В економічному плані він виступає у формі збільшення сімейних доходів, які пов’язані з родинними відносинами та спільним господарюванням.
Це джерело доходів родина використовує як і для цілей внутрішнього споживання, так і для продажу продуктів сільського господарства. Для наочного розкриття цього факту в 9-ому класі учням може бути запропонована така фінансово-математична ситуація:
Задача 4. Родина планує отримати від власного вирощування та продажу картоплі дохід у розмірі 600 гривень. Яку кількість урожаю потрібно зібрати, якщо на рік для всієї родини потрібно 200 кг картоплі, а на ринку картоплю можна продати за ціною 1гривня 20 копійок за 1 кілограм?
Працюючи з класом над цією задачею, однозначної відповіді отримати не можливо, оскільки враховано не всі факти, на які потрібно звернути увагу в плануванні врожаю картоплі. Тому врахування даних задачі приводить до складання нерівності. Нехай х кг картоплі родина продасть за 1 грн. 20 коп. Тоді врожай картоплі повинен задовольняти нерівність:
х - 200 < 60 000 / 120.
Робота з такими даними знайомить учнів із плануванням власних доходів та видатків. Це розвиває такі риси характеру як уважність, організованість, планування власних дій тощо.
Різні види заощаджень також можуть виступати джерелом доходів для родини, якщо вони розміщенні на ринку цінних паперів (акції, облігації, ощадні сертифікати тощо) або вкладені в банки. Методика роботи з такими математичними задачами розглядалася в попередніх пунктах роботи.
Одним із засобів формування бюджету сім’ї є участь родини у суспільному виробництві. Це досягається підприємницькою діяльністю та використанням її результатів.
Мале підприємництво протягом останніх років привертає до себе прискіпливу увагу держави. Вона зацікавлена у розвитку малого підприємництва, бо підприємець має можливість знайти своє місце в економічному просторі держави. Держава від цього отримує податки, збільшуючи валовий внутрішній продукт та число робочих місць у реальній економіці, зменшуючи соціальну напругу. Підприємець, в свою чергу, отримує низькі накладні витрати, можливість отримувати банківські кредити на розвиток власної справи, зменшений податковий тиск, можливість активної участі у виробничому та соціальному житті, реалізацію власних планів. Значення цього факту можливо відобразити такою задачею.
Задача 5. Розвиток малого підприємництва в нашій державі набуває все більшого значення. Побудуйте стовпчасту діаграму динаміки зростання чисельності суб’єктів малого підприємництва та їх доходів в Україні за даними таблиці 2.17.
Ці данні показують, що в Україні створені можливості для підприємницької діяльності, які громадяни використовують для отримання та збільшення власного доходу.
Таблиця 2.17
Динаміка чисельності та доходів суб’єктів малого підприємництва в Україні
Рік |
Кількість суб’єктів малого підприємництва, тис. од. |
Доходи від власності та підприємницької діяльності, млн. грн. |
| 1998 | 1132 | 1160,0 |
| 1999 | 1258 | 1414,0 |
| 2000 | 1421 | 3244,0 |
| 2001 | 1586 | 3934,0 |
За даними цієї ж таблиці при вивченні теми "Графіки функцій" у дев’ятому класі доцільно з учнями побудувати графік зміни середнього доходу суб’єктів підприємницької діяльності в Україні та провести його аналіз як з математичної так і з фінансової сторони. Демонстрація даних таблиці можлива за допомогою кодоскопа.
Розв’язування таких завдань показує учням можливості створення та розширення власного бізнесу, реалізації особистих планів та програм, отримання доходів та покращення добробуту.
В структурі грошових доходів родини суттєвим є отримання доходів за рахунок соціальних гарантій.
Соціальні гарантії надаються в межах соціального захисту інтересів населення. Рівень соціальних гарантій та соціальної допомоги залежить від соціальної політики держави. Він спрямований на підвищення добробуту населення та задоволення мінімально необхідних стандартів життєвого рівня населення. Видами та формами соціального забезпечення населення є соціальні допомоги на випадок безробіття, захворювання чи нещасного випадку на виробництві.
Для аналізу робочої спроможності та доходів громадян в Україні завжди відстежується офіційний рівень безробіття
Вивчаючи, тему “Графіки функцій” у дев’ятому класі учням можна запропонувати проаналізувати графік (мал. 2.13) “Рівень безробіття в Україні” та відповісти на питання:
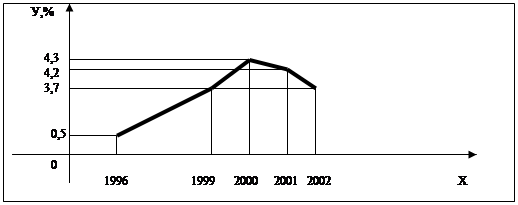
Мал. 2.13. Графік рівня безробіття в Україні
1. Що вибрано за незалежну змінну, а що - за функцію?
2. В якому році рівень безробіття був найбільшим?
3. Як змінювалась кількість безробітних з 1996 до 2001 року?
4. В який період рівень безробіття зростав? спадав?
5. Яка область визначення функції?
6. Яка область значень функції?
Робота з такими даними знайомить учнів з фактами впливу на рівень безробіття: науково-технічний прогрес; втілення в життя новітніх технологій, що заміняють живу працю; міграція працездатних осіб, які шукають можливості більше заробляти тощо.
Також до соціальних гарантій відносяться пенсії, стипендії та надання соціальної допомоги у разі необхідності.
При подальшій роботі з математичними задачами фінансового змісту про сімейний бюджет було звернуто увагу учнів на наявність різних видів соціальних гарантій, які також є джерелом стабілізації доходів родини.
У державі проводиться політика адресного надання соціальної допомоги. До категорій населення, які отримують адресну соціальну допомогу, належать сім’ї з дітьми, віком до трьох років, багатодітні сім’ї, малозабезпечені одинокі громадяни, учасники бойових дій, інваліди війни, особи, які мають особливі заслуги перед Батьківщиною, учасники ліквідації аварії на Чорнобильській АЕС, особи, які мають статус громадян, які постраждали в наслідок Чорнобильської катастрофи та інші.
Крім адресної соціальної допомоги, в Україні діє низка програм, соціально спрямованих на покращення добробуту населення. Однією з них є програма житлових субсидій. Вона захищає сім'ї з низьким рівнем доходів від підвищення цін на житло, комунальні послуги, електроенергію, газ тощо. У зв’язку з цим учням було запропоновано такі задачі:
Задача 8. У Київській області для відшкодування витрат на оплату житлово-комунальних послуг виділено 10 000 тис. грн., а кількість сімей, яким призначено субсидії, становить 200 тис. Який відсоток річного прибутку має кожна з цих родин від користування субсидіями, якщо середньомісячний прибуток кожної родини становить 450 гривень?
Безкоштовні послуги населенню на освіту, охорону здоров'я тощо, є додатковим джерелом надходжень до бюджету сім'ї з бюджетів різних рівнів.
Аналіз різних джерел доходів родини розвиває в учнів фінансовий досвід, вміння застосовувати математичні закони для розрахунку власних грошей. Це показує, що рівень життя громадян залежить від їх діяльності. Напрошується висновок: чим більше в державі заможніх людей, тим багатшою є держава в цілому. Тому потрібно акцентувати увагу учнів на тому, що від особистої діяльності кожного з них як громадянина України залежить як фінансовий стан родини, так і загальний економічний розвиток держави.
Розглянемо як можна ознайомити учнів із статтями витрат сімейного бюджету на уроках математики.
У результаті ознайомлення учнів із різними доходами та видатками родини узагальнюючим завданням виступає складання бюджету родини. Доречно запропонувати в дев‘ятому класі під час вивчення теми “Елементи прикладної математики” учням заповнити дома таблицю 2.20.
Таблиця 2.20
Сімейний бюджет
Доходи |
Витрати |
||||
| в грн. | у % | в грн. | у % | ||
|
1).Заробітна плата. 2). Доход від особистого господарства. 3). Доходи від інших джерел, які пов'язані з власністю. 4).Пенсії, стипендії, соціальна допомога. 5). Доходи від цінних паперів. 6). Інше. |
1).Поточні витрати. 2).Одноразові витрати. 3). Заощадження. 4). Податки. 5). Різні обов'язкові платежі. 6). Інше. |
||||
| Всього: | Всього: |
На наступному уроці, під час перевірки домашнього завдання, слід проаналізувати результати і з’ясувати відповіді на такі запитання:
1. Як обчислюється відсоток доходів, який припадає на заробітну плату та на інші статті доходів?
2. Чим відрізняється обчислення доходів родини від обчислення видатків?
3. Коли можна вважати, що бюджет родини дефіцитний (видатки більші за доходи)? Профіцітний (доходи більші за видатки)? Збалансований?
4. Яким чином можна розпорядитись залишком коштів, якщо бюджет профіцитний? Як поповнити доходи, якщо бюджет дефіцитний?
5. Якого виду бюджету краще всього дотримуватись у родині, у державі в цілому?
Потім учням було роздано зведений бюджет України за 2003 рік та проведено аналіз наведених даних. Учням пропонувалося ввести свої пропозиції щодо покращення Державного бюджету.
Така робота навчає учнів робити аналіз числових даних та привчає їх корисно розпоряджатися власними коштами та державними коштами.
Ознайомлення учнів з елементами складання бюджету сприяє розумінню фінансових операцій родини, підприємства, фірми та держави в цілому. Учні навчаються ширше бачити можливості застосування власних математичних знань як в повсякденному житті, так і в науковому використанні математичного аналізу різних даних. Це привчає робити правильні висновки та прогнозувати подальші власні дії в різних життєвих ситуаціях.
Система задач на сімейний бюджет, яка відображена в додатку Г. Ці задачі сприяють поступовому ознайомленню учнів основної школи з різними фінансовими термінами та поняттями, які важливі для складання розумного сімейного бюджету родини.
2.5. Задачі на страхування та їх особливості
Формування в Україні ринкової економіки та створення різних механізмів ринкових операцій загострює проблеми збереження власних коштів. Зростання ризику у всіх сферах людського життя та господарської діяльності обумовлене необхідністю захисту громадян від можливих витрат та збитків.
Страхування в умовах ринкової економіки ґрунтується на попередньому створенні страхових фондів зі страхових внесків та на відшкодуванні збитків потерпілим. Кожна людина повинна знати, як вона може зменшити свій ризик і скільки їй це коштуватиме. Отже, страхування – це спосіб захисту майнових інтересів громадян в умовах ринкової економіки.
У курсі математики основної школи не можливо висвітлити всі особливості страхової справи, оскільки основні засади страхування пов’язані, в першу чергу, з економічним ризиком, який ґрунтується на поняттях теорії ймовірності. Розділ теорії ймовірності сьогодні не включено до програми основної школи, хоча деякі його засади розкриваються учням лише в старшій школі. Тому ознайомлення з усіма математичними розрахунками страхування в основній школі неможливе, але основні поняття та розрахунки страхування як напрямку фінансової сфери людської діяльності, можуть бути відображені в задачах основної школи.
Страхування як система економічних відносин передбачає наявність двох суб’єктів – страховика та страхувальника. Страховик – це юридична особа (наприклад, акціонерне товариство), яка має право на здійснення страхової діяльності. Страхувальник – це особа, яка страхує власне майно або власні інтереси, сплачує страхові внески та має право на отримання компенсації при настанні страхового випадку.
Законом України “Про страхування” [41] визначено, що об'єктами страхування можуть бути майнові інтереси, що не суперечать законодавству України. Вони пов'язані з:
· життям, здоров'ям, працездатністю та додатковою пенсією страхувальника або застрахованої особи (особисте страхування);
· володінням, користуванням і розпорядженням майна (майнове страхування);
· відшкодуванням страхувальником заподіяної ним шкоди особі або її майну, а також шкоди, заподіяної юридичній особі (страхування відповідальності).
Відповідно розрізняють страхування добровільне та обов’язкове. Добровільне страхування - це страхування, яке здійснюється на основі договору між страхувальником і страховиком. Загальні умови і порядок здійснення добровільного страхування визначаються правилами страхування, що встановлюються страховиком самостійно. Видами добровільного страхування можуть бути: страхування життя; страхування від нещасних випадків; медичне страхування; страхування транспорту; страхування вантажів та багажу; страхування на випадок пожежі та стихійних явищ; страхування майна; страхування кредитів тощо. В Україні здійснюються такі види обов'язкового страхування: медичне страхування; особисте страхування медичних працівників на випадок інфікування вірусом імунодефіциту людини при виконанні ними службових обов'язків; особисте страхування працівників пожежної охорони; страхування спортсменів вищих категорій; страхування життя і здоров'я спеціалістів ветеринарної медицини; особисте страхування від нещасних випадків на транспорті; страхування засобів водного транспорту; страхування врожаю; страхування цивільної відповідальності оператора ядерної установки за ядерну шкоду, яка може бути заподіяна внаслідок ядерного інциденту; страхування працівників, які беруть участь у наданні психіатричної допомоги; страхування тварин; страхування відповідальності суб'єктів туристичної діяльності; страхування відповідальності морського судновласника тощо.
Ознайомлення учнів із різними видами страхування та деякими їх особливостями може бути здійснене за допомогою навчальних математичних задач. Розглянемо, наприклад, такі задачі.
Задача 1. Визначити, яке страхове відшкодування отримає сільськогосподарський виробник, якщо він застрахує урожай за таких умов, що страхова компанія відшкодує збитки у розмірі 70% від недоотримання урожаю. Середня врожайність з 1га - 23 ц, а фактично отримали 20 ц з га. Площа посіву 200га. Закупівельна ціна пшениці за 1 ц дорівнює 50 грн.
Для розв’язання цієї задачі потрібно відповісти на запитання:
1. Якою повинна бути ціна врожаю?
23 × 200 × 50 = 230 000 (грн.)
2. Яка фактична ціна отриманого урожаю?
20 × 200 × 50 = 200 000 (грн.)
3. Яка величина збитків?
230 000 – 200 000 = 30 000 (грн.)
4. Яке страхове відшкодування?
30 000 × 0,7 = 21 000 (грн.)
Відповідь: 21 000 гривень.
Для слабких учнів можуть бути роздані картки де складений план розв’язування задачі. Сильніші учні самостійно складають план та розв’язують задачу.
Робота з такою задачею не лише вчить учнів обчислювати відсотки від певної фінансової суми, а й показує важливість страхування в реальних умовах життя.
В системі страхування застосовують кілька видів фінансових розрахунків та франшизи.
Для визначення величини страхового внеску в страховій практиці часто використовується страховий тариф, який визначається як ставка страхового внеску з одиниці страхової суми за визначений період страхування.
Задача 6. Страховий внесок за майно становив 300 грн. при страховому тарифі 0,2 %. Яка страхова сума застрахованого майна?
Для розв’язання цієї задачі важливо усвідомити, що страховий тариф показує відсоткове відношення між страховим внеском і страховою сумою, тобто 300 грн. є 0,2 % від страхової суми. Тому знаходження страхової суми полягає у знаходження числа за його частиною:
300 : 0,002 = 150 000 (грн.)
Відповідь: 150 000 грн.
У страхуванні майна найпоширенішим є страхування за дійсною вартістю майна, що визначається на день укладання договору. В цьому випадку страхове забезпечення дорівнює величині збитків, тобто повне покриття збитків страхувальника. Для відображення цього виду страхування під час вивчення теми “ Функція” учням може бути запропоновано задати функціональну залежність між збитками та страховим відшкодуванням і побудувати відповідний графік функції, якщо збитки дорівнюють а грн.
Це завдання не викликає труднощів, але показує механізм фінансових розрахунків у цій ситуації.
Наступний вид розрахунків – страхування за системою пропорційної відповідності. Воно передбачає виплату страхового відшкодування, яке розраховується за формулою 2.10:
![]() , (2.10)
, (2.10)
де Q – страхове відшкодування ,
S - страхова сума за угодою (страховий внесок),
T – вартісна оцінка об’єкта страхування,
W – фактична сума збитків.
Це дуже поширений вид страхування. Учням пропонується з формули 2.10 знайти вирази, за яким обчислюється страхова сума за угодою, фактична сума збитків та вартісна оцінка об’єкта страхування. Це знайомить учнів із головними величинами страхової справи та показує математичні залежності між ними.
У 9 класі учням під час вивчення теми “Нерівності” можна запропонувати завдання, яке демонструє використання наведеної вище формули. Наведемо приклад.
Задача 2. Визначити, на яку суму варто застрахувати майно, якщо вартісна оцінка квартири становить 12 000 умовних одиниць, можлива сума збитків 10 000 у. о., а страхове відшкодування повинно бути більше за 8 000 у. о.
Розв’язування цієї задачі можна оформити таким чином.
Складаємо на основі формули 2.10 нерівність:
12 000 × (S/10 000) > 8 000.
Звідси маємо:
S/10 000 > 2/3;
S > 6 666,(6).
Відповідь: бажано застрахувати більше, ніж на 6667 у. о.
В ході аналізу отриманого результату учні спостерігають залежність: покриття збитків тим вище, чим менше різниця між вартісною оцінкою об’єкта страхування та страховою сумою.
Наступний вид – страхування за системою першого ризику. В цьому випадку відбувається виплата відшкодування у розмірі збитків, але в межах страхової суми.
На етапі ознайомлення учнів із задачею, важливо пояснити, що під “першим ризиком” у страховій справі розуміють ризик, вартісна оцінка якого не перевищує страхової суми. При дії даної системи страхування, всі збитки у межах страхової суми відшкодовуються повністю. Збитки, які перевищують страхову суму (другий ризик), страховиком не відшкодовуються. Тому розв’язання цієї задачі полягає у виконанні наступної дії: 321 500 – 234 000 = 87 500 (грн.)
У страховій справі особиста участь страхувальника у покритті збитків виражається через франшизу. Франшиза - частина збитків, що не відшкодовується страховиком згідно з договором страхування, тобто це звільнення страховика від покриття збитків на певну суму. Вона може бути встановлена у відсотках або в абсолютних розмірах щодо страхової суми, вартісної оцінки об’єкту або розміру збитків.
Розрізняють умовну та безумовну франшизи. Умовна франшиза звільняє страховика від відповідальності за збитки, які не перевищують встановленої франшизи і зобов’язує його покривати збитки повністю, якщо розмір їх перевищує франшизу.
Безумовна франшиза звільняє страховика від компенсації перших х % страхової суми, незалежно від величини збитків. За будь-яких умов вона вилучається з зобов’язань страховика, тому вона безумовна. В цьому випадку страхове відшкодування завжди дорівнює різниці між збитками та безумовною франшизою.
Під час вивчення теми “Функції та їх властивості” учням пропонується задати функцію та побудувати їх графік за такими даними задачі:
Задача 4. Задати функціональну залежність між збитками та страховим відшкодуванням, зробити порівняльний аналіз отриманих результатів, якщо:
1. Страхова сума становить 200 тис. грн., а умовна франшиза становить 20% від страхової суми.
2. Страхова сума становить 200 тис. грн., а безумовна франшиза становить 20% від страхової суми.
Міркування над даними задачі проводить до наступних результатів.
Нехай х – сума збитків, а у(х) – страхове відшкодування. В умові задачі франшиза становить 200 000 × 0,2 = 40 000 (грн.)
1. У випадку умовної франшизи повинні виконуватись умови:
· якщо величина збитків менше за 40000 грн., то страхове відшкодування дорівнює 0, тобто у = 0;
· якщо величина збитків більше за 40000 грн., то страхове відшкодування дорівнює сумі збитків, тобто у = х.
Врахування цих даних, приводить до такої функції:
![]()
В отриманої функції область визначення та область значення лише додатні числа, тому графік функції розташований лише в першій чверті координатної площини. Враховуючи все вище зазначене, отримаємо графік, який зображений на малюнку 2.14.
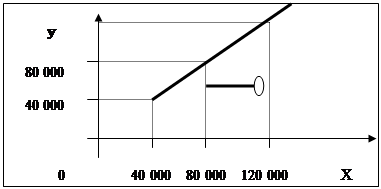
Мал.2.14. Графік страхових відшкодувань у випадку умовної франшизи
2.
У
випадку безумовної франшизи страхове відшкодування завжди дорівнює
різниці між збитками та безумовною франшизою, тобто ![]() .(мал.2.15)
.(мал.2.15)
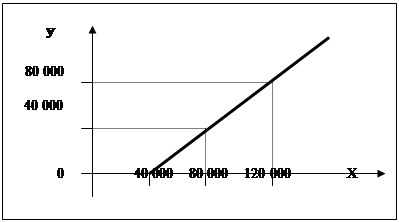
Мал.2.15. Графік страхових відшкодувань у випадку безумовної франшизи
У отриманої функції область визначення та область значення лише додатні числа, тому графік функції розташований лише в перший чверті координатної площини (мал.2.15.)
Проводячи порівняльний аналіз отриманих графіків, треба звернути увагу учнів на відмінності, які виникли з особливостей кожного виду франшизи.
Надалі, учням пропонується самостійно задати числові характеристики для різних видів страхування та побудувати графіки функціональної залежності між збитками і страховим відшкодуванням за цими умовами.
Для узагальнення дій різних видів страхування учням можуть бути запропоновані задачі, де відбувається страхування за декількома видами.
Задача 5. Обчислити страхові відшкодування за викрадений автомобіль вартістю 8200 грн., якщо він був застрахований у трьох різних компаніях на умовах: в першій - на суму 6 500 грн. за безумовною франшизою у розмірі 5 %, в другій - на суму 8 000 грн. за безумовною франшизою у розмірі 3 %, а в третій - на суму 8 100 грн. за умовною франшизою у розмірі 8 %.
В цьому прикладі важливо звернути увагу учнів на те, що у випадку страхування в декількох місцях франшиза обчислюється від відсоткової вартості застрахованого об’єкта, яка попадає на даний договір страхування. Тому обчислення будуть відбуватись за такою схемою:
1. Загальна страхова сума становить: 6 500+8 000+8 100 = 22 600 (грн.)
2. Відповідно частки страховиків від загальної суми становлять:
(6 500 : 22 600) × 100 » 28,76 % – для першого,
(8 000 : 22 600) × 100 » 35,40 % – для другого,
(8 100 : 22 600) × 100 » 85,84 % – для третього.
3. Страхові виплати з врахуванням франшизи становлять:
8 200 × (0,2876 - 0,05) = 1 948,32 (грн.) – для першого,
8 200 × (0,3540 - 0,03) = 2 656,8 (грн.) - для другого,
8 200 × (0,8584 - 0,08) = 6 382,88 (грн.) - для третього.
Відповідь: 1 948,32 грн., 2 656,8 грн., 6 382,88 грн.
Робота з такими даними показує учням особливості, які відбуваються при розрахунках у випадку одночасного страхування одного об’єкта в декількох місцях на різних умовах.
Таким чином, розв’язуючи математичні задачі на страхування учні усвідомлюють такі фінансові поняття, як:
· страхове відшкодування - страхова виплата, яка здійснюється страховиком у межах страхової суми за договорами майнового страхування і страхування відповідальності при настанні страхового випадку;
· страхова сума - грошова сума, в межах якої страховик відповідно до умов страхування, зобов'язаний провести виплату при настанні страхового випадку;
· страховий внесок – сума, яка сплачується страхувальником за страхування;
· страховий тариф - ставка страхового внеску з одиниці страхової суми за визначений період страхування або відношення страхового внеску до страхової суми об’єкту страхування;
· вартісна оцінка об’єкта страхування;
· фактична сума збитків;
· умовна та безумовна франшиза;
· інші.
Особливості роботи з задачами на страхування в курсі математики основної школи полягають у трактуванні різних страхових термінів в ході розв’язування задач. Тоді показується математична залежність в страховій системі. Учні вчаться застосовувати математичні знання у звичайних страхових ситуаціях, які відбуваються в повсякденному житті. Важливість страхової справи в умовах ринкової економіки підкреслюється та розкривається змістом математичних задач на страхування, які ми пропонуємо ввести в курс основної школи (додаток Д). Через систему задач на страхування в курсі математики основної школи відбувається ознайомлення учнів з різними страховими поняттями (додаток Є). Задачі на страхування в курсі математики основної школи відображають можливий соціально-фінансовий напрямок захисту власних інтересів кожного громадянина українського суспільства.
2.6. Організація, проведення та аналіз результатів педагогічного експерименту
Основні теоретичні положення активізації пізнавальної діяльності при роботі з математичними задачами фінансового змісту, які висвітлені в роботі, були реалізовані під час проведення експериментального дослідження у шевченківській загальноосвітній школі. Для уточнення активізації пізнавальної діяльності було використано дослідження пізнавального інтересу учнів 9-А класу (14 учнів), його формування та розвиток, що виступає головним показником в процесі пізнавальної діяльності учнів.
Робота проводилась з вересня 2006 по травень 2007 р.
Мета експерименту полягала в перевірці робочої гіпотези дослідження. Її перевірка вимагала, в першу чергу, виявлення ефективності впливу запропонованої системи задач на активізацію навчання та формування пізнавального інтересу до математики. В ході експерименту з‘ясовувались доступність та ефективність системи математичних задач фінансового змісту, яка спрямована на формування та розвиток пізнавального інтересу до математики, можливість використання різних прийомів і методів роботи з ними, роль запропонованих задач в процесі навчання математики та в процесі розширення фінансово-математичної обізнаності учнів.
Під час розв‘язання проблеми та перевірки гіпотези розв‘язувались як основні, так і часткові завдання. Зокрема:
1. З‘ясувати спрямованість інтересів учнів 9 класів до учбових предметів та місце математики серед них.
2. З‘ясувати особливості пізнавального інтересу до математичних задач фінансового змісту.
3. Визначити методи та засоби роботи з математичними задачами фінансового змісту, що сприяють формуванню та розвитку пізнавального інтересу учнів.
Дослідження проводилось протягом трьох етапів.
На першому етапі була сформульована робоча гіпотеза, визначались конкретні задачі дослідження та розроблявся план дослідної роботи. На початковому етапі дослідження особлива увага приділялась розгляду та вивченню літератури, аналізу психологічних, педагогічних та методичних праць з даної проблеми та розробці тестів, метою яких було виявлення пізнавального інтересу учнів до математичних задач фінансового змісту та математики в цілому.
На другому етапі проводився пошуковий педагогічний експеримент. В ході експерименту здійснювалась цілеспрямована робота з активізації пізнавальної діяльності учнів при розв’язуванні математичних задач фінансового змісту на уроках математики. В процесі відстежувались зміни у ставленнях учнів до математики та їх успішності. За допомогою різних методик досліджувались рівні пізнавального інтересу учнів.
На третьому етапі за допомогою тестів та анкет проводилось опитування учнів з метою порівняння даних в експериментальних та контрольних класах. Метою опитування було виявлення впливу спеціально підібраної системи математичних задач фінансового змісту та методики її використання на розвиток пізнавального інтересу учнів до математики.
Остаточна робота полягала в обробці, перевірці та уточненні даних, отриманих у процесі експерименту, формулюванні висновків.
Спостереження на уроках математики проводились за планом, який включав: аналіз використання математичних задач фінансового змісту та методів роботи з ними; спостереження за уважністю, самостійністю в теоретичній та практичній діяльності учнів; виявлення інтересу до вивчення математичних основ та, особливо, до роботи із запропонованими задачами.
У процесі спостереження зверталась увага на питання, які ставлять учні до вчителів та товаришів, відповіді за власним бажанням, зацікавленість у роботі з математичними задачами фінансового змісту, прагнення зрозуміти життєве значення та застосування даних задач та прагнення поповнювати свої знання самостійно шляхом розв‘язування задач з додаткових джерел.
На початку експерименту за допомогою тестів було з‘ясоване питання про наявність та предметну спрямованість інтересів учнів, а також рівень їх сформованості.
Перший тест включав у себе завдання, де крім вибору відповіді на питання, в деяких випадках, потрібно ще й обґрунтувати свій вибір. (див. Додаток Ж.)
Серед професій, які вказували учні у відповідях на перше питання, зустрічалися такі як бухгалтер, фінансист, економіст, менеджер. Це свідчить про зацікавленість учнів у фінансових операціях та підтверджує ідею необхідності збільшення фінансової освіти в школі.
У відповідях на друге питання, на жаль мало хто з учнів знайшов реальне застосування власних математичних знань. Багато відповідей вказували на те, що учні не знаходять життєвого значення для математики: для допомоги виконувати домашні завдання молодшому брату, для отримання гарної оцінки тощо. Аналіз відповідей на наступні питання тесту подано у таблиці 2.21.
Таблиця 2.21
Аналіз тесту на виявлення рівня пізнавального інтересу до математичних задач фінансового змісту та рівня знань фінансово-математичних операцій і законів
| Запитання | Так | Ні | Не знаю |
| Чи мрієте Ви стати багатими? | 98 % | 0 % | 2 % |
| Чи можливо з грошей робити гроші? | 86 % | 3 % | 11 % |
| Чи бажаєте дізнатися більше про фінансово-математичні закони? | 65 % | 35 % | - |
| Чи потрібно вивчати фінансові задачі та закони в школі? | 95 % | 5 % | - |
| Чи зустрічаєтесь Ви з фінансовими проблемами в житті? | 78 % | 22 % | - |
| Чи подобаються Вам фінансово-математичні розрахунки? | 16 % | 1 % | 83 % |
| Чи допоможе, на Ваш погляд, вивчення фінансових особливостей в школі розбагатіти кожному громадянину країни? | 86 % | 5 % | 9 % |
| Чи є в нашій країні економічна нестабільність? | 64 % | 29 % | 7 % |
Данні таблиці показують, що у більшості учнів виникає інтерес до фінансової тематики, але програмою основної школи не передбачено ознайомлення учнів з цим напрямком життя. Тому для забезпечення первинних знань фінансових операцій, термінів, законів, ознайомлення з елементарними поняттями фінансового світу доцільно до задач, які розглядаються на уроках математики, включити математичні задачі фінансового змісту.
Другий тест було побудовано за селективним методом, який потребував вибору однієї або декількох альтернатив із множини запропонованих (див. додаток З).
З метою виявлення предметної спрямованості інтересів учнів, було запропоновано перше завдання в тесті: "Виписати предмети, які Ви вивчаєте в стовпчик та напроти кожного поставити відповідне число: 3 – якщо Ви любите предмет; 2 – якщо предмет Вам подобається; 1 - якщо Ви ставитись до нього байдуже; 0 – якщо Вам предмет зовсім не подобається." Обчисливши середній бал, отримали данні діаграми, які відображені на мал. 2.16.
Як видно з діаграми, алгебра займає п’яте місце серед шкільних предметів,
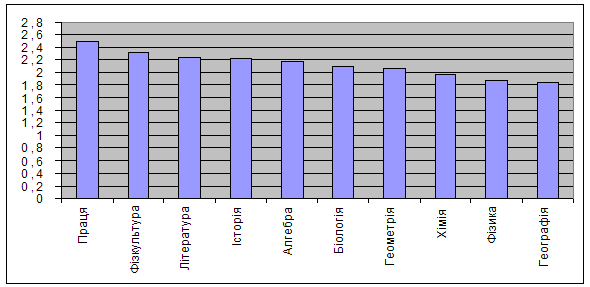
Мал. 2.16. Середній бал інтересу учнів до навчальних предметів
На запитання "Чим Вам подобається математика?" учні відповідали:
· своїм науковим змістом, багато важливих та цікавих знань – 26 %;
· тим, як веде урок вчитель – 37 %;
· задачами, які ми розглядаємо –22 %;
· легко вивчати та цікаво виконувати домашнє завдання – 14 % ;
· математика допомагає мені в житті – 1 %.
На запитання "Що не подобається в математиці?" були такі відповіді:
· не бачу застосування знань у житті, необхідності у вивченні -23 %;
· багато не розумію, важко вчити -17 %;
· не подобаються задачі, які ми розглядаємо - 13 %;
· на уроках нецікаво - 27 %;
· багато домашнього завдання - 20 % .
Цікавими виявились відповіді і на запитання: "Чим подобається займатися на уроках математики?". Тут учні назвали:
· слухати викладача – 23 %;
· розв‘язувати задачі та завдання разом із класом - 41 % ;
· самостійно розв‘язувати задачі та працювати з підручником –14 % ;
· виконувати самостійні та контрольні роботи – 13 %;
· займатися зайвими справами, які не пов‘язані з математикою – 9 %.
Ці данні вказують на відсутність інтересу до математики, бо коли існує інтерес, то завдання виконуються легко та із задоволенням. Тоді учні використовують додаткову літературу, розв’язують нестандартні завдання і прагнуть до самостійного поширення знань, вмінь та навичок. Певним чином це позначилось і у відповідях на запитання "Які завдання подобається виконувати з математики?". Розподіл був такий:
· 13 % - легкі;
· 25 % - які потребують не дуже складних міркувань;
· 6 % - важкі, підвищеної складності;
· 11 % - на кмітливість та уважність;
· 45 % - пов‘язані з реальним життям.
Аналіз відповідей учнів на це питання ще раз підтверджує, що для підвищення інтересу учнів до вивчення математики необхідно в курс математики основної школи вводити задачі пов‘язані з життєвою реальністю, а не задачі, які не знаходять відображення у повсякденному житті.
Аналіз тестів дав можливість простежити рівень пізнавального інтересу учнів до вивчення математики та фінансових законів через певний проміжок часу. Підсумковий тест проводився в експериментальному класі на кінець проведення експерименту.
Підсумковий тест (див. додаток І) виявлення рівня інтересу учнів до математики та до розв‘язування математичних задач фінансового змісту показав, що в експериментальному класі математика вже стала займати третю позицію щодо інтересу учнів до шкільних предметів, а задачі з фінансовим змістом серед всіх навчальних задач зайняли третє місце, після задач пов’язаних із життям та задач - жартів.
У процесі дослідження було проведено аналіз підручників з математики, за якими відбувається навчання в основній школі, на наявність в них математичних задач фінансового змісту. Були отримані данні наведені в табл.2.22.
За результатами таблиці 2.22 можна зробити такі висновки:
· кількість математичних задач фінансового змісту дуже обмежена в шкільному курсі математики, серед них зустрічаються комерційні задачі на сімейний бюджет, банківські розрахунки, але зовсім відсутні задачі на податки та цінні папери;
· кількість математичних задач фінансового змісту трохи збільшується при вивченні теми “Елементи прикладної математики” в 9-ому класі, але майже всі вони стосуються складних відсотків нарахування грошей, але діти майже зовсім не ознайомлюються з математичними операціями, які використовуються в фінансових розрахунках;
· рідко використовуються задачі з недостачею даних, із зайвими даними, не наводяться приклади математичних задач фінансового змісту із заданими даними у вигляді таблиць, графіків, діаграм;
· відсутні задачі для самостійного фінансового обрахування життєвих даних, що знижує показ реальності математичних операцій та законів;
· мала кількість математичних задач фінансового змісту, а при викладанні нового матеріалу їх відсутність, знижує інтерес учнів до вивчення абстрактних математичних понять та предмету математика в цілому.
Таблиця 2.22
Математичні задачі фінансового змісту в діючих підручниках з математики
|
загальна кількість завдань |
задачі на банківські розрахунки | задачі на податки | задачі на цінні папери | задачі на страхування |
задачі на сімейний бюджет та комерційні (купівля – продаж) |
|||||||
| Підручник | Клас | |||||||||||
|
Бевз Г.П. Алгебра 7-9, 2003 р. |
||||||||||||
| 9 | 375 | 3 | 0 | 0 | 0 | 3 | ||||||
| Кравченко В.Р. та інш. Алгебра, 9, 2003 р. | 9 | 1049 | 8 | 0 | 0 | 0 | 3 | |||||
Головне місце в ході дослідження займав експеримент, який включав у себе використання математичних задач фінансового змісту в процесі вивчення математики та різних методів роботи над ними. Це дало змогу виявити особливості пізнавального інтересу учнів до математичних задач фінансового змісту та організувати експериментальне навчання, яке проводилось у звичайних умовах без змін ходу учбового процесу, у відповідності до програм навчання математики.
Під час проведення формуючого експерименту ставилась задача комплексного використання математичних задач фінансового змісту різних видів з метою активізації пізнавальної діяльності учнів та розвитку пізнавального інтересу учнів до вивчення математики та перевірки гіпотези, яка була сформульована в результаті спостережень та теоретичного аналізу проблеми.
Експериментальне навчання проводилось в окремому класі у відповідності з чинною програмою. Вивчення матеріалу відбувалось за діючими підручниками, проте робота була посилена по використанню математичних задач фінансового змісту та певних методів роботи з ними, що сприяло підвищенню інтересу учнів до вивчення математики та, в загальному, активізувало пізнавальну діяльність учнів.
Задачний матеріал було розроблено та розподілено майже за всіма темами, що вивчаються в курсі математики основної школи. Він відповідав зазначеним вимогам до змісту задач та методиці їх використання. Час для роботи над задачами даної групи з‘являвся за рахунок заміни типових задач підручника математичними задачами фінансового змісту. Крім того, велика кількість задач обговорювалась на уроці, а подальша робота виносилась на самостійне дослідження.
Результати експерименту показали, що використання задач фінансово-економічного змісту при вивченні математики в середній школі сприяє підвищенню інтересу учнів до математики та підвищенню їх успішності.
ВИСНОВКИ
Результати проведеного теоретичного дослідження та педагогічного експерименту дозволяють нам сформулювати висновки щодо їх практичного використання:
1. Активізація пізнавальної діяльності учнів – це перехід до більш високого рівня активності та самостійності учнів у процесі навчання, який стимулюється розвитком пізнавального інтересу, та відбувається завдяки удосконаленню методів та прийомів навчального процесу.
2. Показниками та ознаками прояву активності та інтересу учнів у процесі роботи над задачею є:
· постановка запитань;
· відстеження помилок в процесі роботи над задачею;
· використання отриманих раніше знань;
· прагнення розв’язувати нестандартні задачі;
· пошук цікавих математичних фактів, використання набутих математичних знань у повсякденному житті;
· самостійне створення задач;
· допомога одноліткам у розв’язанні складніших завдань;
· пошук альтернативних способів розв’язування задач тощо.
3. Розв’язування математичних задач фінансового змісту та введення їх в учбову програму основної школи сприяє створенню необхідного емоційного настрою, активності учнів у навчанні та розширенню сфери практичного застосування вмінь та навичок учнів, отриманих у процесі вивчення математики.
4. Математичні прикладні задачі фінансового змісту виконують:
· освітню функцію, оскільки їх використання спрямоване на формування у школярів системи знань, вмінь та навичок на різних етапах навчання;
· розвиваючу функцію, бо робота з ними розвиває вміння осмислювати зміст понять, застосувати здобуті знання на практиці, аналізувати результати, робити відповідні узагальнення, порівняння та висновки;
· виховну функцію, бо економічне та фінансове виховання на уроках математики може здійснюватися насамперед завдяки цим задачам;
· контролюючу функцію як навчальні задачі.
5. Для досягнення активізації пізнавальної діяльності учнів при роботі з математичними задачами фінансового змісту потрібно дотримуватись виконання таких вимог до задач:
· задача повинна бути правильно подана (вчитель пояснює важливість її розв‘язання для подальшої роботи та набуття відповідних вмінь);
· задача повинна бути зрозуміла учням, тобто пояснені всі терміни, які зустрічаються в задачі, ситуація описана в задачі відома та цікава для учнів із життєвої необхідності, вимога задачі повинна викликати інтерес;
· задача повинна бути посильною учням, тобто учні повинні мати досвід роботи з такими задачами або можуть самостійно набути необхідних знань;
· задача повинна викликати інтерес завдяки хоч одній умові: зовні цікавого формулювання, незвичної постановки запитання чи процесу розв’язування задачі;
· задача повинна розвивати життєвий досвід учнів, показувати можливість використання шкільних знань у різних життєвих ситуаціях.
6. Система математичних задач фінансового змісту виступає ефективним засобом активізації пізнавальної діяльності учнів основної школи. Це відбувається на основі підвищення пізнавального інтересу учнів, досягається акцентуванням уваги на значенні знань в реальному житті та реалізується вибором методів, форм і засобів навчання.
7. Використання учителями математичних задач фінансового змісту потребує певної їх підготовки, а запропонована система задач можливе бути введена в курс математики основної школи завдяки заміні учбових задач та завдань із “застарілою” фабулою новими задачами фінансового змісту.
8. Результати експериментальної перевірки та досвід впровадження системи математичних задач фінансового змісту в практику основної школи підтверджують правильність висунутої гіпотези. Зокрема, вони свідчать про її позитивний вплив на весь навчально-виховний процес, а саме: використання системи математичних задач фінансового змісту сприяє:
· формуванню пізнавального інтересу учнів до вивчення математики;
· підвищенню успішності та якості математичної підготовки учнів;
· формуванню в учнів знань, вмінь та навичок використання математичних знань у фінансовій сфері людської діяльності;
· розвитку логічного мислення, творчої активності та пізнавальної самостійності школярів.
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
1. Ананьев Б.Г. Психология и проблемы человекознания : Избранные психологические труды. – М.: Изд-во Моск. псих.- соц. ин-та, 1996. – 384 с.
2. Аристова Л.П. Активность учения школьника. - М.: Просвещение, 1968. - 210 с.
3. Бабанский Ю.К. Проблемное обучение как средство повышения эффективности учения школьников. - Ростов- на-Дону: 1970. - 31 с.
4. Бевз Г.П. Алгебра: Підручник для 7-9 кл. серед. шк. - К.: Освіта, 2003. - 303 с.
5. Бевз Г.П. Методика викладання математики. - К.: Вища школа, 1989. - 376 с.
6. Бевз Г.П. Методика розв'язування алгебраїчних задач у 6-8 класах. Посібник для вчителя. - К.: Рад. шк., 1975. - 204 с.
7. Брушлинський А.В. Психология мышления и проблемного обучения. – М.: Знания, 1983. – 96 с.
8. Буряк В.К. Самостоятельная работа учащихся. - М.: Просвещение, 1984. - 64с.
9. Виготский Л.С. Собрание сочинений: В 6-ти томах. – М.: Педагогика, 1982. – Т.4 Детская психология / Под ред. Д.Б. Эльконина. – 432 с.
10. Винокуров Е.Ф. Школьное экономическое образование и учитель математики // Математика в школе. – 2001.- №2. – С.23- 27.
11. Габай Т. В. Учебная деятельность и ее средства. - М.: МГУ, 1988. - 255 с.
12. Гнеденко Б.В. Математика и математическо образование в современном мире. - М.: Просвещение, 1985. - 190 с.
13. Голанд Е.Я. О развитии самостоятельности и творческой активности учащихся в процесе обучения // Воспитание познавательной деятельности и самостоятельности учащихся. Ч.1. – Казань: 1969. – С.78 - 89.
14. Груденов Я.И. Совершенствование методики роботы учителя математики. - М. : Просвещение, 1990. - 224 с.
15. Гурова Л.Л. Психологический анализ решения задач. – Воронеж: 1976. – 340 с.
16. Данилов М.А. Воститание у школьников самостоятельности и творческой активности. – Казань: Тат.кн.изд-во, 1963.- 96 с.
17. Дубинчук Е.С. Активизация познавательной деятельности учащихся средних професионально-технических училищ в процесе обучения математике. - К.: Вища школа, 1987. - 101 с.
18. Дутка Г.Я. Практикум з математики для економістів. - Л.: 1998. – 362 с.
19. Есипов Б.П. Самостоятельная работа учащихся на уроках. - М.: Учпедгиз, 1961. - 239 с.
20. Закон України “Про банки і банківську діяльність” № 2121-III від 07.12.2000
21. Закон України “Про загальну середню освіту” // Освіта. – 1997. – 20-27 серпня. – С.6-11.
22. Закон України “Про оподаткування прибутку підприємств” від 12.08.1994
23. Закон України “Про освіту” // Голос України. – 1996. – 25 квітня. – С.1-6.
24. Закон України “Про податок на додану вартість” від 01.10.1997.
25. Закон України “ Про страхування” від 7.03.1996
26. Закон України “Про цінні папери і фондову біржу” (1991) Мін.фін. України № 04-305 від 30.09.1991 р.
27. Зимняя И.А. Педагогическая психология: Учебник для вузов. – М.: Логос, 2001. – 384 с.
28. Ігнатенко М.Я., Соколенко Л.О. Реалізація прикладної спрямованості шкільного курсу математики як засіб активізації навчально-пізнавальної діяльності учнів. Навчальний посібник. - К.: ІЗМН, 1997. - 76 с.
29. Кабанова– Меллер Е.Н. Формирование приемов умственной деятельности и умственное развитие учащихся. – М.: Просвещение, 1968. – 160 с.
30. Колягин Ю.М. Задачи в обучении математике. Ч.1.Математические задачи как средство обучения и развития учащихся. - М.: Просвещение, 1977.- 110с.
31. Колягин Ю.М. Задачи в обучении математике. Ч.2. Обучение математике через задачи и обучение решению задач. - М.: Просвещение, 1977. - 144 с.
32. Конституція України. – К.: Юрінком, 1996. – 80 с.
33. Кордемский Б.А. Увлечь школьников математикой. - М.: Просвещение, 1981. - 112 с.
34. Корсакова О.К. Методи навчання, що формують в учнів досвід перетворювальної діяльності. – К.: ФАДА ЛТД, 2000. – 28 с.
35. Крутецкий В.А. Психология математических способностей школьников. - М.: Просвещение, 1968. - 432 с.
36. Кудрявцев П.Д. Современная математика и ее преподавание. – М.: Наука, 1980. – 144с.
37. Левинберг Л.М., Ібрагимов Р.А. Активизация познавательной деятельности младших школьников ( на материале математики). – Ташкент: Из-во “Фан” АН УзССР, 1991. – 216с.
38. Матушкина З.П. Формирование умений решать задачи при обучении математике учащихся 4-5 классов. Дис… канд. пед. наук.: 13.00.02. - М.,1985. - 223 с.
39. Матюшкин А.М. Проблемные ситуации в мышлении и обучении. - М.: Педагогика, 1972. - 208 с.
40. Махмутов М.И. Организация проблемного обучения в школе. – М.: Просвещение, 1977. – 240с.
41. Менчинская Н.А. Задачи в обучении / В кн. Педагогическая энциклопедия. Т.2 - М.: Просвещение, 1965. - С.3-16.
42. Педагогічний словник / за ред. М.Д. Ярмаченка - К.: Пед. думка, 2001. - 516 с.
43. Пидкасистый П.И. Самостоятельная деятельность учащихся. – М.: Педагогика, 1972. – 184 с.
44. Податкова система України / За ред. Федосеева В.М. – К.: Либідь,1994. – 464 с.
45. Пономарев Я.А. Психология творения: Избр. псих. труды – Воронеж: Модэк, 1999. – 480 с.
46. Пономаренко О.І. Сучасний фінансовий аналіз і фінансові числення // У світі математики. - 1997. - т.3. в.1.– С. 28-42.
47. Про затвердження інструкції “Про прибутковий податок з громадян.”// Все про бухгалтерський облік. - № 67 (492) від 24.07.2000. – С.12 – 38.
48. Про податки і збори населенню України: Посібник / М.Я. Азаров, Г.І. Бондаренко, П.В. Мельник та інші – Ірпінь: Академія ДПС України, 2000. – 182 с.
49. Психологические основы формирования личности в педагогическом процессе / Под ред. А. Коссановски, Х. Кюка, И. Ломпшер, Г. Розенфелда. Перевод с немецкого. – М.: Педагогика, 1981. – 224 с.
50. Ростовецкая Л.А. Самостоятельность личности в познании и общении. – Ростов-на-Дону: РГПИ, 1975. – 297с.
51. Рубинштейн С.Л. Основы общей психологии. – М.: Педагогика, 1989. – 320с.
52. Cкаткин М.Н. Совершенствование процесса обучения. Проблемы и суждения. – М.: Педагогика, 1971. – 206 с.
53. Скрипченко О.В., Лисянська Т.М., Скрипченко Л.О. Довідник з педагогіки та психології. – К.: Видавництво Національного педагогічного університету імені М.П. Драгоманова, 2002. – 216 с.
54. Cрода Г.В. Воспитание активности и самостоятельности учащихся в обучении. – М.: Изд-во АПН РСФСР, 1956. – 56 с.
55. Статистичний збірник України за 2000 рік. - К.:, 2001. – 432 с.
56. Фридман Л.М. Учитесь учиться математике: Кн. для учащихся. – М.: Просвещение, 1985. – с.112.
57. Фридман Л.М. Логико-психологический анализ школьных учебных задач. – М.: Педагогика, 1977. – 208 с.
58. Фридман Л.М., Кулагина И.Ю. Психологический справочник учителя. – М.:Просвещение, 1991. – 288с.
59. Фридман Л.М., Турецкий Е.Н. Как научиться решать задачи. – М.: Просвещение, 1984. – 175 с.
60. Харламов И.Ф. Педагогика в вопросах и ответах. – М.: Гардарики, 2001. – 253 с.
61. Харламов И.Ф. Педагогика. – Минск: Універсітэцкае, 2000. – 560 с.
62. Шамова Т.И. Активизация учения школьников. –М.: Педагогика, 1982 – 208 с.
63. Шапиро И.М. Использование задач с практическим содержанием в преподавании математики. - М.: Просвещение, 1990. - 96 с.
64. Шорох-Троцький С.Н. Методика арифметики для учителей начальных школ. – М.,1915. – 78 с.
65. Щукина Г.И. Актуальные вопросы формирования интереса в обучении. – М.: Просвещение, 1984. – 176 с.
66. Щукина Г.И. Педагогические проблемы формирования познавательных интересов учащихся. – М.: Педагогика, 1988. – 203 с.
67. Якиманская И.С. Знания и мышление школьника.– М.: Знание, 1985. – 78с.
68. Якиманская И.С. Личностно ориентированное обучение в современной школе. – М.,1996. –96 с.
| Шпоры по Госам МСХА | |
|
... Она состоит из общих основ эк теории, микрои макроэкономики и интерэкономики (мировой экономики). В общ осн эк теории дается: хар-ка понятия общества ... По хар прогнозир: -пассивный: предпол, что регион,пр-е не мог активно воздействов на св будущ(внеш ср). -активный -самые активные действия пр-я,региона на вн ср. -вариантный: связ ... Управление мотивационными факторами: это след. компоненты - орг-ция труда (мастерство раб-ка, значимость, самост-ть), психологич. состояние раб-ков (чувство ответ-сти, собст-ой ... |
Раздел: Остальные рефераты Тип: реферат |
| Аналіз виконання і планування місцевих бюджетів | |
|
... ІНСТИТУТ УАБС До захисту допускаю: завідувач кафедри обліку і фінансів, д.е.н., професор В.М. Тимофєєв ДИПЛОМНА РОБОТА АНАЛІЗ ВИКОНАННЯ І ПЛАНУВАННЯ ... Навч. пос. / М.І.Ка-рлін, Л.М.Горбач, Л.Я.Новосад та ін.; За заг. ред. д.е.н., проф. Навч.-метод, посібник для самост. вивч. дисц. / М.А.Гапонюк, В.П.Яцюта, А.Є.Буряченко, А.А.Славкова. |
Раздел: Рефераты по финансовым наукам Тип: дипломная работа |
| Економічна ефективність виробництва зерна та шляхи її підвищення у ... | |
|
КУРСОВИЙ ПРОЕКТ "ЕКОНОМІЧНА ЕФЕКТИВНІСТЬ ВИРОБНИЦТВА ЗЕРНА ТА ШЛЯХИ ЇЇ ПІДВИЩЕННЯ У ПРИВАТНОМУ СІЛЬКОГОСПОДАРСЬКОМУ ПІДПРИЄМСТВІ "КУМАРИ ... Для цього при визначенні ефективності виробництва продовольчого зерна розраховують розмір праці на 1 ц зерна і на 100 грн. валової продукції, фуражного зерна - витрати праці на 1 ц ... У ум. = Ѭ У0П1 / Ѭ П1 = 29906,8 / 988 = 30,27 ц/га |
Раздел: Рефераты по ботанике и сельскому хозяйству Тип: курсовая работа |
| Разработка поточных технологических линий обслуживания животных для ... | |
|
Содержание Аннотация Введение 1. Анализ производственной деятельности КСП. Характеристика хозяйства Производство продукции растениеводства ... продукции, грн/ц; чел- ч/ц Зм - материальные затраты, грн; |
Раздел: Рефераты по технологии Тип: реферат |
| Ответы на госудаственные экзамены по психологии ЮУрГУ | |
|
1. Принцип единства сознания и деятельности как конкретизация принципа детерминизма Деятельность - динамическая система взаимодействий субъекта с ... Становление Я-концепции. обусловленное широким со ц.-культурным контекстом, возникает в обстоятельствах обмена Д-ю между людьми, в ходе коего субъект "смотрится как в зеркало в ... Процесс становления Л-ти связан с осознанием иерархий мотивов (Выготский-характеризовал соц. среду Т-я подр-ка -необ-сть Т-я их интересов => устойчивая иерархия мотивов ... |
Раздел: Рефераты по психологии Тип: шпаргалка |
