Курсовая работа: Анализ и синтез механизмов
1. Структурное и кинематическое исследование плоско-рычажного механизма
1.1 Структурный анализ механизма
1.1.1 Наименование звеньев и их количество
Дана структурная схема механизма. Механизм предназначен для преобразования вращательного движения кривошипа 1 в возвратно-поступательное движение ползуна 5.
Для данного кривошипно-ползунного механизма (изображенного на 1 листе графического задания), наименование звеньев и их количество приведено в таблице 1.
Таблица 1
|
Наименование звена |
Буквенное обозначение звена |
Действительный размер, (мм) |
Чертежный размер, (мм) |
| 1. Кривошип |
О1А |
200 | 40 |
| 2. Кулиса | АС | 1000 | 200 |
| 3. Ползун | В | - | - |
| 4. Шатун | СD | 500 | 100 |
| 5. Ползун | D | - | - |
| 6. Неподвижная стойка |
О1О2О3 |
Х1=400 X2=600 |
80 120 |
Всего звеньев 6 из них подвижных n=5
1.1.2 Кинематические пары и их классификации
Для данного кривошипно-ползунного механизма кинематические пары и их классификации приведены в таблице 2.
Таблица 2
|
Обозначение КП |
Звенья составляющие КП |
Вид движения |
Подвижные КП (класс) |
Высшая или низшая |
|
О1 |
0–1 | вращательное |
P1(V) |
низшая |
| А | 1–2 | вращательное |
P1(V) |
низшая |
|
B3 |
2–3 | поступательное |
P1(V) |
низшая |
|
О2 |
0–3 | вращательное |
P1(V) |
низшая |
|
C4 |
2–4 | вращательное |
P1(V) |
низшая |
|
С5 |
4–5 | вращательное |
P1(V) |
низшая |
|
S5 |
0–5 | поступательное |
P1(V) |
низшая |
Всего звеньев 6 из них подвижных n=5
1.1.3 Степень подвижности механизма
Число степеней свободы (степень подвижности) кривошипно-ползунного механизма определяется по формуле П.Л. Чебышева:
![]()
где n – число подвижных звеньев механизма;
P1 – число одноподвижных кинематических пар.
Т.к. W=1 механизм имеет одно ведущее звено и это звено №1.
1.1.4 Разложение механизма на структурные группы (группы Ассура)
Проведенное разложение кривошипно-ползунного механизма на структурные группы (группы Ассура) приведено в таблице 3.
Таблица 3
|
Группа |
Эскиз группы |
Звенья составляющие группу |
КП в группе |
Степень подвижности |
Класс, порядок, модификация группы |
|
|
внутренние |
внешние |
|||||
| Ведущая группа |
О1 А
|
1–0 |
О1 |
А | W=1 |
1 кл. 1 вид. |
| Группа Ассура |
О2
B |
2–3 |
B3(2–3) |
А (2–1) О2(0–3) |
W=1 | II кл., 2 пор., 3 модиф. |
| Группа Ассура |
D С |
4–5 |
D4(4–5) |
C (2–4) D5(0–5) |
W=1 | II кл., 2 пор., 2 модиф. |
1.1.5 Структурная формула механизма (порядок сборки)
![]()
К механизму 1 класса, 1 вида состоящего из звеньев 0 и 1 присоединена группа Ассура II класса, 2 порядка, 3 модификации состоящая из звеньев 2 и 3. К этой группе присоединена группа Ассура II класса, 2 порядка, 2 модификации состоящая из звеньев 4 и 5.
1.2 Кинематический анализ механизма
Цель: определение положения звеньев и траектории движения их точек, определение скоростей и ускорений точек звеньев, а также определение угловых скоростей и угловых ускорений звеньев по заданному закону движения ведущего звена.
1.2.1 Графический метод кинематического анализа
Заключается в построении графиков перемещении, скорости и ускорения последнего звена механизма в функции от времени (построение кинематических диаграмм) и определение их истинных значений.
1.2.1.1 Построение планов положения механизма
Кинематический анализ начинаем с построения плана положения механизма. Для этого должны быть известны:
1) размеры звеньев механизма, м;
2) величина и направление угловой скорости
ведущего звена ![]() .
.
Размеры звеньев механизма равны:

Выбираем масштабный коэффициент длины: ![]()
Нулевым положением является крайнее нижнее положение ползуна 5 – начало преодоления силы F п.с.
Построенный план положения механизма представлен на листе №1 графической части курсового проекта.
Длина отрезков, изображающих звенья механизма на чертеже, будут равны:

1.2.1.2 Построение диаграммы перемещений
Диаграмма перемещений пятого звена является графическим изображением закона его движения.
Проводим оси координат (графическая часть, лист
№1). По оси абсцисс откладываем отрезок ![]() ,
представляющий собой в масштабе
,
представляющий собой в масштабе ![]() время
Т(с) одного периода (время одного полного оборота выходного звена):
время
Т(с) одного периода (время одного полного оборота выходного звена):
![]()
Масштабный коэффициент времени:
![]()
Откладываем перемещение выходного звена по оси
ординат, принимаем за нулевое – крайнее нижнее положение ползуна. Масштабный
коэффициент будет равен: ![]()
Построенная диаграмма представлена на листе №1 графической части курсового проекта.
1.2.1.3 Построение диаграммы скорости
Построение диаграммы скорости осуществляется методом графического дифференцирования диаграммы угла поворота (методом хорд).
Н1=25 мм – расстояние до полюса графического дифференцирования (Р1).
Масштабный коэффициент диаграммы угловой скорости:
![]()
Построенная диаграмма скорости представлена на листе №1 графической части курсового проекта.
1.2.1.4 Построение диаграммы ускорения
Построение диаграммы ускорения осуществляется методом графического дифференцирования диаграммы угловой скорости.
Н2=15 мм – расстояние до полюса графического дифференцирования (Р2).
Масштабный коэффициент диаграммы углового ускорения:
![]()
Построенная диаграмма ускорения представлена на листе №1 графической части курсового проекта.
Истинные значения перемещения, скорости и ускорения приведены в сводной таблице 4.
Таблица 4
| № положения |
l, м |
v, м/с |
a, м/с2 |
| 0 | 0,00 | 0,00 | 14,56 |
| 1 | 0,07 | 1,02 | 6,48 |
| 2 | 0,15 | 0,99 | -1,38 |
| 3 | 0,22 | 0,88 | -0,63 |
| 4 | 0,29 | 0,92 | 1,64 |
| 5 | 0,36 | 1,11 | 2,97 |
| 6 | 0,46 | 1,33 | 1,95 |
| 7 | 0,56 | 1,34 | -3,19 |
| 8 | 0,65 | 0,59 | -28,31 |
| 9 | 0,62 | -2,69 | -35,90 |
| 10 | 0,29 | -4,53 | 0,94 |
| 11 | 0,02 | -1,20 | 19,41 |
1.2.2 Графоаналитический метод кинематического анализа
1.2.2.1 Построение плана скорости
Исходные данные:

Угловая скорость ведущего звена
![]()
1. Абсолютная скорость точки А1 на конце ведущего звена 1
![]()
![]()
2. Масштабный коэффициент:

Длинна вектора скорости точки А:
![]()
3. Скорость средней точки первой группы Ассура – точки В определяем через скорости крайних точек этой группы А и О2.
Скорость точки В относительно точки А:
![]()
Скорость точки В относительно точки О2:
![]()
Отрезок ![]() представляет
собой вектор скорости точки B, решаем графически.
представляет
собой вектор скорости точки B, решаем графически.
4. По свойству подобия находим на плане скоростей точку С, которая принадлежит звену 2 и 4, то есть является крайней точкой второй группы Ассура.
Длину вектора ![]() определяем
из соотношения:
определяем
из соотношения:
![]()
откуда:
![]()
Отрезок ![]() представляет
собой вектор скорости точки С.
представляет
собой вектор скорости точки С.
5. Скорость средней точки второй группы Ассура D4 определяем через скорости крайних точек этой группы С и О3.
Скорость точки D4 относительно точки С:
![]()
Скорость точки D4 относительно точки О3:
![]()
Отрезок ![]() представляет
собой вектор скорости точки D4, решаем
графически.
представляет
собой вектор скорости точки D4, решаем
графически.
Центры тяжести весомых звеньев определяем по свойству подобия.
6. Пользуясь планом скорости, определяем истинные (абсолютные) значения скоростей точек механизма:
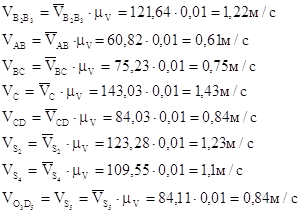
7. Определяем абсолютные величины угловых скоростей звеньев:

где lАВ = lАВ∙μl =89,38· 0,005 = 0,4469 м
1.2.2.2 Построение плана ускорения
Исходные данные: 1. Кинематическая схема механизма (1 лист)
2. Угловая скорость ведущего звена ![]()
3. План скоростей для заданного положения.
1. Абсолютное ускорение точки А на конце ведущего звена:

![]()
2. Масштабный коэффициент:

Длина вектора ускорения точки А1:
![]()
3. Ускорение средней точки первой группы Ассура – точки В2 определяем через ускорения крайних точек этой группы А и О2.
Ускорение точки В2 относительно точки А:
![]()
![]()
![]()
![]()
Ускорение точки В относительно точки О2:
![]()
Величина ускорения Кориолиса определяется по модулю формулой:
![]()
Длина вектора, изображающего ускорение Кориолиса на плане ускорений равна:
![]()
Для определения направления ускорения Кориолиса
вектор относительной скорости ![]() поворачиваем
на 90о по направлению угловой скорости
поворачиваем
на 90о по направлению угловой скорости ![]() .
.
Из конца вектора ![]() проводим
линию действия релятивного ускорения
проводим
линию действия релятивного ускорения ![]() параллельную
звену АВ.
параллельную
звену АВ.
Решаем графически.
4. По свойству подобия находим на плане ускорения точку С, которая принадлежит звеньям 2 и 4, то есть является крайней точкой второй группы Ассура.
![]()
откуда:
![]()
5. Ускорение средней точки второй группы Ассура – точки D4 определяем через ускорения крайних точек этой группы C и О3, причем точка D4 принадлежит звену 4 и совпадает с точкой D5.
Ускорение точки D4 относительно точки С:
![]()
![]()
![]()
![]()
Ускорение точки D4 относительно точки О3:
![]()
![]()
Решаем графически.
Центры тяжести весомых звеньев определяем по свойству подобия
6. Пользуясь планом ускорений, определяем истинные (абсолютные) значения ускорений точек механизма:
![]()

7. Определяем абсолютные величины угловых ускорений звеньев:

На этом кинематическое исследование кривошипно-ползунного механизма завершено.
2. Силовой анализ плоско-рычажного механизма
2.1 Определение внешних сил
К звену 5 приложена сила полезного сопротивления FПС, направление которой указано на схеме.
Величина FПС = 1200 Н.
Масса звеньев:
![]()
где q = 10 – вес 1 метра длины звена, кг/м
li – максимальная длина звена, м.
Определяем массы звеньев:

Собственные моменты инерции звеньев относительно оси, проходящей через центр тяжести:
![]()
где ![]() - масса
звена, кг.
- масса
звена, кг.
![]() – длинна звена, м.
– длинна звена, м.
Определяем моменты инерции:

Определяем силы веса по формуле:
![]()
(Принимаем g=10 м/с2 – ускорение свободного падения)

Определяем силы инерции по формуле:
![]()
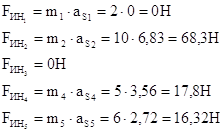
Определяем моменты пар сил инерции по формуле:
![]()

Определяем плечи переноса сил по формуле:
![]()
![]()
![]()
Направление внешних сил проставлено на кинематической схеме механизма (лист №1 графической части курсового проекта)
2.2 Определение внутренних сил
2.2.1 Вторая группа Ассура
Структурная группа 2 класса, 2 порядка, 2 модификации.
Изображаем эту группу отдельно. Действие
отброшенных звеньев 3 и 0 заменяем силами реакций ![]() и
и
![]() .
.
В точке О3 на звено 5 действует сила
реакции со стороны стойки – ![]() ,
которая перпендикулярна СО3, но неизвестна по модулю и
направлению.
,
которая перпендикулярна СО3, но неизвестна по модулю и
направлению.
В точке С на звено 4 действует сила реакции со
стороны звена 2 – ![]() , тк величина и
направление не известно, раскладываем её на тангенсальную и нормальную.
, тк величина и
направление не известно, раскладываем её на тангенсальную и нормальную.
Линия действия тангенсальной составляющей силы реакции перпендикулярна СD. Величину и направление находим из уравнения моментов сил относительно точки D.
![]()
![]()
При расчете величина ![]() получилась со знаком (+), т.е.
Направление силы выбрано верно.
получилась со знаком (+), т.е.
Направление силы выбрано верно.
Векторное уравнение сил, действующих на звенья 4 и 5:
![]()
Это векторное уравнение решаем графически, т.е. строим план сил.
Принимаем масштабный коэффициент:
![]()
Вектора сил будут равны:


Из плана сил находим:

2.2.2 Первая группа Ассура
Структурная группа 2 класса, 2 порядка, 3 модификации.
Изображаем эту группу отдельно. Действие отброшенных звеньев заменяем силами реакций.
В точке С на звено 2 действует сила реакции со
стороны звена 4 – ![]() , которая равна
по модулю и противоположно направлена найденной ранее силе
, которая равна
по модулю и противоположно направлена найденной ранее силе ![]() , т.е.
, т.е. ![]() .
.
В точке О2 на звено 3 действует сила
реакции со стороны стойки – ![]() ,
которая известна по точке приложения, перпендикулярна звену АВ и неизвестна по
модулю и направлению.
,
которая известна по точке приложения, перпендикулярна звену АВ и неизвестна по
модулю и направлению.
В точке А на звено 2 действует сила реакции со
стороны звена 1 – ![]() .
.
Линия действия этой силы неизвестна, поэтому
раскладываем её на нормальную и тангенсальную. Величину ![]() находим из уравнения
моментов сил относительно точки В.
находим из уравнения
моментов сил относительно точки В.
![]()

При расчете величина ![]() получилась со знаком (+), т.е.
Направление силы выбрано верно.
получилась со знаком (+), т.е.
Направление силы выбрано верно.
Векторное уравнение сил, действующих на звенья 2 и 3:
![]()
Это векторное уравнение решаем графически, т.е. строим план сил.
Принимаем масштабный коэффициент:
![]()
Вектора сил будут равны:

Из плана сил находим:

2.2.3 Определение уравновешивающей силы
Изображаем ведущее звено и прикладываем к нему все действующие силы. Действие отброшенных звеньев заменяем силами реакций.
В точке А на звено 1 действует сила реакции со
стороны звена 2 -![]() , которая равна
по величине и противоположна по направлению найденной ранее силе реакции
, которая равна
по величине и противоположна по направлению найденной ранее силе реакции ![]() , т.е.
, т.е. ![]() .
.
В точке О1 на звено 1 действует сила
со стороны звена 0 – ![]() , которую
необходимо определить.
, которую
необходимо определить.
Для определения ![]() составим
векторное уравнение сил звена 1:
составим
векторное уравнение сил звена 1:
![]()
Это векторное уравнение решаем графически, т.е. строим план сил.
Вектора сил будут равны:

Из плана сил находим:
![]()
Для уравновешивания звена 1 в точках А и О1
прикладываем уравновешивающие силы – ![]() перпендикулярно
звену.
перпендикулярно
звену.
Сумма моментов относительно точки О1:
![]()
![]()
Знак ![]() – положительный,
следовательно, направление силы выбрано, верно.
– положительный,
следовательно, направление силы выбрано, верно.
Уравновешивающий момент:
![]()
Построенный силовой анализ кривошипно-ползунного механизма изображен на листе №1 графической части курсового проекта.
2.2.4 Определение уравновешивающей силы методом Н.Е. Жуковского
Для определения уравновешивающей силы методом Н.Е. Жуковского строим повернутый в любую сторону план скоростей. Силы, действующие на звенья механизма, переносим в соответствующие точки рычага Жуковского без изменения их направления.
Плечи переноса сил ![]() и
и
![]() на рычаге находим из
свойства подобия:
на рычаге находим из
свойства подобия:
![]()
![]()
Направление плеча переноса ![]() от точки S2 за точку А.
от точки S2 за точку А.
Направление плеча переноса ![]() от точки S4 к точке С.
от точки S4 к точке С.
Уравнение моментов сил, действующих на рычаг относительно полюса:
![]()

Уравновешивающий момент:
![]()
2.2.5 Определение погрешности.
Сравниваем полученные значения уравновешивающего момента, используя формулу:

Допустимые значения погрешности менее 3% следовательно, расчеты произведены верно.
На этом силовой анализ кривошипно-ползунного механизма закончен.
3. Расчет маховика
3.1 Момент сопротивления движению
Приведенный к валу кривошипа момент сопротивления движению определяем по формуле:
![]()
где: ![]() = 1200
Н – сила полезного сопротивления, действует только на рабочем ходу. На холостом
ходу
= 1200
Н – сила полезного сопротивления, действует только на рабочем ходу. На холостом
ходу ![]() = 0.
= 0.
w1 = 6,81м/с – угловая скорость ведущего звена (кривошипа).
VS5 –скорость выходного звена (ползуна), определенная для 12 положений в первой части курсового проекта.
Значения ![]() для
12 положений механизма сводим в таблицу 5.1.
для
12 положений механизма сводим в таблицу 5.1.
Таблица 5.1.
| № |
w1 1/с |
VS5 м/с |
|
|
|
| 0 | 6,81 | 0,000 | 0 | 0,00 | 0,0 |
| 1 | 6,81 | 1,022 | 1200 | 180,13 | 72,1 |
| 2 | 6,81 | 0,985 | 1200 | 173,67 | 69,5 |
| 3 | 6,81 | 0,876 | 1200 | 154,35 | 61,7 |
| 4 | 6,81 | 0,917 | 1200 | 161,71 | 64,7 |
| 5 | 6,81 | 1,111 | 1200 | 195,81 | 78,3 |
| 6 | 6,81 | 1,332 | 1200 | 234,79 | 93,9 |
| 7 | 6,81 | 1,344 | 1200 | 236,85 | 94,7 |
| 8 | 6,81 | 0,592 | 1200 | 104,37 | 41,7 |
| 9 | 6,81 | -2,691 | 0 | 0,00 | 0,0 |
| 10 | 6,81 | -4,533 | 0 | 0,00 | 0,0 |
| 11 | 6,81 | -1,202 | 0 | 0,00 | 0,0 |
3.2 Приведенный момент инерции рычажного механизма
Приведенный момент инерции определяем по формуле:

где: ![]() = 0,016кгм2
– момент инерции звена 1;
= 0,016кгм2
– момент инерции звена 1;
m5 = 6 кг – масса пятого звена;
Значения ![]() для
12 положений механизма сводим в таблицу 5.2.
для
12 положений механизма сводим в таблицу 5.2.
Таблица 5.2.
| № |
|
m5, кг |
w1 1/с |
VS5,м/с |
|
|
|
| 0 | 0,016 | 6 | 6,81 | 0,000 | 0,0000 | 0,0160 | 1,60 |
| 1 | 0,016 | 6 | 6,81 | 1,022 | 0,1352 | 0,1512 | 15,12 |
| 2 | 0,016 | 6 | 6,81 | 0,985 | 0,1257 | 0,1417 | 14,17 |
| 3 | 0,016 | 6 | 6,81 | 0,876 | 0,0993 | 0,1153 | 11,53 |
| 4 | 0,016 | 6 | 6,81 | 0,917 | 0,1090 | 0,1250 | 12,50 |
| 5 | 0,016 | 6 | 6,81 | 1,111 | 0,1598 | 0,1758 | 17,58 |
| 6 | 0,016 | 6 | 6,81 | 1,332 | 0,2297 | 0,2457 | 24,57 |
| 7 | 0,016 | 6 | 6,81 | 1,344 | 0,2337 | 0,2497 | 24,97 |
| 8 | 0,016 | 6 | 6,81 | 0,592 | 0,0454 | 0,0614 | 6,14 |
| 9 | 0,016 | 6 | 6,81 | -2,691 | 0,9380 | 0,9540 | 95,40 |
| 10 | 0,016 | 6 | 6,81 | -4,533 | 2,6608 | 2,6768 | 267,68 |
| 11 | 0,016 | 6 | 6,81 | -1,202 | 0,1870 | 0,2030 | 20,30 |
3.3 Построение графиков (метод Виттенбауэра)
По данным таблицы 5.1. строим диаграмму изменения момента сопротивления в функции от угла поворота кривошипа МС=МС(φ1).
По оси абсцисс откладываем отрезок произвольной длинны, соответствующий полному обороту кривошипа, и делим его на 12 частей, соответствующих 12 положениям механизма.
Масштабный коэффициент угла поворота:
![]()
Примем ![]() =
360 мм.
=
360 мм.
![]()
По оси ординат откладываем значение МС для каждого положения механизма в определенном масштабе.
Примем μм = 2,5 Нм/мм.
Графически интегрируя график МС=МС(φ1), строим график работы сил сопротивления в зависимости от угла поворота кривошипа АС=АС(φ1).
Примем Н = 60 мм.
Масштабный коэффициент графика работы:
![]()
Работа сил сопротивления за один оборот кривошипа равна работе движущих сил. Соединяя прямой линией начало и конец графика работы сил сопротивления, строим график работы движущих сил АД=АД(φ1).
Графически дифференцируя график АД=АД(φ1) на графике МС=МС(φ1) строим график МДМД(φ1) = const (горизонтальная прямая линия).
Величина движущего момента, Нм.
![]()
Строим график ΔТ= ΔТ(φ1) в масштабе μТ= μА=2,63Нм/мм.
По данным таблице 5.2. строим график изменения
приведенного момента инерции в функции от угла поворота JПР=JПР(φ1).
Ось угла поворота направляем вертикально вниз, откладываем на ней отрезок ![]() и делим его на 12 частей
и делим его на 12 частей
Значение JПР откладываем по горизонтальной оси для каждого положения
Примем μJ = 0,01 кгм2/мм.
Имея диаграммы ΔТ= ΔТ(φ1) и JПР=JПР(φ1) строим диаграмму энергомасс ΔТ= ΔТ(JПР), для этого сводим одноименные точки и соединяем их плавной линией.
3.4 Определение момента инерции маховика
Для определения момента инерции маховика определяем углы наклона касательных к диаграмме Виттенбауэра Ψmax и Ψmin.
![]()
где: wСР =w1 = 6,811/с – угловая скорость кривошипа,
δ=0,04 – коэффициент неравномерности хода.
![]() 0,0916
0,0916
Ψmax=5,23o
![]() 0,0846
0,0846
Ψmin=4,83o
К Диаграмме Виттенбауэра проводим касательные под найденными углами к горизонтальной оси JПР. Эти касательные пересекают ось ординат в точках а и в. замеряем отрезок ав.
Момент инерции маховика:
![]()
По найденному моменту инерции маховика определяем его размеры. Маховик конструктивно выполняем в виде сплошного чугунного диска диаметром – d и шириной – в. Момент инерции сплошного диска относительно его оси равен:
![]()
где: g = 7200 кг/м2 – удельная плотность чугуна,
d – диаметр диска,
в - ширина диска.
Примем ![]() ,
тогда:
,
тогда:
![]()
Откуда:
![]()
![]()
dо = в = 0,17256 м – диаметр отверстия под вал.
4. Синтез зубчатого механизма
4.1 Геометрический синтез зубчатого зацепления
Задачей геометрического синтеза зубчатого зацепления является определение его геометрических размеров и качественных характеристик (коэффициентов перекрытия, относительного скольжения и удельного давления), зависящих от геометрии зацепления.
4.2 Определение размеров внешнего зубчатого зацепления
Исходные данные:
Z4 = 12 – число зубьев шестерни,
Z5 = 30 – число зубьев колеса,
m2 = 10 – модуль зацепления.
Шаг зацепления по делительной окружности
![]() 3,14159 · 10 = 31,41593 мм
3,14159 · 10 = 31,41593 мм
Радиусы делительных окружностей
![]() 10 · 12 / 2 = 60 мм
10 · 12 / 2 = 60 мм
![]() 10 · 30 / 2 = 150 мм
10 · 30 / 2 = 150 мм
Радиусы основных окружностей
![]() 60 · Соs20o = 60 · 0,939693 = 56,38156 мм
60 · Соs20o = 60 · 0,939693 = 56,38156 мм
![]() 150 · Соs20o = 150 · 0,939693 = 140,95391 мм
150 · Соs20o = 150 · 0,939693 = 140,95391 мм
Коэффициенты смещения
Х1 – принимаем равным 0,73 т. к. Z4 =12
Х2 – принимаем равным 0,488 т. к. Z5 =30
Коэффициенты смещения выбраны с помощью таблиц Кудрявцева.
![]() 0,73 + 0,488 = 1,218
0,73 + 0,488 = 1,218
Толщина зуба по делительной окружности
![]() 31,41593 / 2 + 2 · 0,73 · 10 · 0,36397 = 21,02192 мм
31,41593 / 2 + 2 · 0,73 · 10 · 0,36397 = 21,02192 мм
![]() 31,41593 / 2 + 2 · 0,488 · 10 · 0,36397 = 19,26031 мм
31,41593 / 2 + 2 · 0,488 · 10 · 0,36397 = 19,26031 мм
Угол зацепления
Для определения угла зацепления вычисляем:
![]() 1000 · 1,218 / (12 + 30) = 29
1000 · 1,218 / (12 + 30) = 29
С помощью номограммы Кудрявцева принимаем ![]() =26о29'=26,48о
=26о29'=26,48о
Межосевое расстояние
![]() (10·42/2) · Соs20o / Cos26,48o=210·0,939693
/ 0,89509 = 220,46446 мм
(10·42/2) · Соs20o / Cos26,48o=210·0,939693
/ 0,89509 = 220,46446 мм
Коэффициент воспринимаемого смещения
 (42 / 2) · (0,939693 / 0,89509 – 1) = 21 · 0,04983 = 1,04645
(42 / 2) · (0,939693 / 0,89509 – 1) = 21 · 0,04983 = 1,04645
Коэффициент уравнительного смещения
![]() 1,218 – 1,04645 = 0,17155
1,218 – 1,04645 = 0,17155
Радиусы окружностей впадин
![]() 10 · (12 / 2 – 1 – 0,25 + 0,73) = 54,8 мм
10 · (12 / 2 – 1 – 0,25 + 0,73) = 54,8 мм
![]() 10 · (30 / 2 – 1 – 0,25 + 0,488) = 142,38 мм
10 · (30 / 2 – 1 – 0,25 + 0,488) = 142,38 мм
Радиусы окружностей головок
![]() 10 · (12 / 2 + 1 + 0,73 – 0,17155) =75,5845 мм
10 · (12 / 2 + 1 + 0,73 – 0,17155) =75,5845 мм
![]() 10 · (30 / 2 + 1 + 0,488 – 0,17155) =163,1645 мм
10 · (30 / 2 + 1 + 0,488 – 0,17155) =163,1645 мм
Радиусы начальных окружностей
![]() 56 · 0,939693 / 0,89509 = 62,98984 мм
56 · 0,939693 / 0,89509 = 62,98984 мм
![]() 150 · 0,939693 / 0,89509 = 157,47461 мм
150 · 0,939693 / 0,89509 = 157,47461 мм
Глубина захода зубьев
![]() (2 · 1 – 0,17155) · 10 = 18,2845 мм
(2 · 1 – 0,17155) · 10 = 18,2845 мм
Высота зуба
![]() 18,2845 + 0,25 · 10 = 20,7845 мм
18,2845 + 0,25 · 10 = 20,7845 мм
Проверка:
1. ![]()
62,98984 + 157,47461 = 220,46445
условие выполнено
2. ![]()
220,46446 – (54,8 + 163,1645) = 0,25 · 10
220,46446 – 217,9645 = 2,5
условие выполнено
3. ![]()
220,46446 – (134,176 + 75,5845) = 0,25 · 10
220,46446 – 217,9645 = 2,5
условие выполнено
4. ![]()
220,46446 – (60 + 150) = 1,04645 · 10
220,46446 – 210 = 10,4645
условие выполнено
4.3 Построение элементов зубчатого зацепления
Принимаем масштаб построения:
![]() 0,0004
0,0004![]() = 0,4
= 0,4 ![]()
На линии центров колес от линии W откладываем
радиусы начальных окружностей (![]() и
и ![]() ), строим их так, чтобы
точка W являлась их точкой касания.
), строим их так, чтобы
точка W являлась их точкой касания.
Проводим основные окружности (![]() и
и ![]() ), линию зацепления n – n касательно к
основным окружностям и линию t – t, касательно к начальным окружностям через точку W. Под углами aW к межосевой
линии проводим радиусы
), линию зацепления n – n касательно к
основным окружностям и линию t – t, касательно к начальным окружностям через точку W. Под углами aW к межосевой
линии проводим радиусы ![]() и
и ![]() и отмечаем точки А, В
теоретической линии зацепления.
и отмечаем точки А, В
теоретической линии зацепления.
Строим эвольвенты, которые описывает точка W прямой АВ при
перекатывании её по основным окружностям. При построении первой эвольвенты
делим отрезок AW на четыре равные части. На линии зацепления n – n откладываем
примерно 7 таких частей. Также 7 частей откладываем на основной окружности ![]() от точек А и В в разные
стороны. Из полученных точек на основной окружности проводим радиусы с центром
О1 и перпендикуляры к радиусам. На построенных перпендикулярах
откладываем соответственное количество частей, равных четверти расстояния AW. Соединив
полученные точки плавной кривой получаем эвольвенту для первого колеса.
Аналогично строим эвольвенту для второго зубчатого колеса.
от точек А и В в разные
стороны. Из полученных точек на основной окружности проводим радиусы с центром
О1 и перпендикуляры к радиусам. На построенных перпендикулярах
откладываем соответственное количество частей, равных четверти расстояния AW. Соединив
полученные точки плавной кривой получаем эвольвенту для первого колеса.
Аналогично строим эвольвенту для второго зубчатого колеса.
Строим окружности головок обоих колес (![]() и
и ![]() ).
).
Строим окружности впадин обоих колес (![]() и
и ![]() ).
).
Из точки пересечения эвольвенты первого колеса
с делительной окружностью этого колеса ![]() откладываем
половину толщины зуба 0,5 S1 по делительной
окружности. Соединив полученную точку с центром колеса О1 получаем
ось симметрии зуба. На расстоянии шага по делительной окружности строим еще два
зуба. Аналогично строим зубья второго колеса.
откладываем
половину толщины зуба 0,5 S1 по делительной
окружности. Соединив полученную точку с центром колеса О1 получаем
ось симметрии зуба. На расстоянии шага по делительной окружности строим еще два
зуба. Аналогично строим зубья второго колеса.
Определяем активную часть линии зацепления (отрезок ав).
Строим рабочие участки профилей зубьев. Для этого из центра О1 проводим дугу радиуса О1а до пересечения с профилем зуба. Рабочим участком зуба является участок от полученной точки до конца зуба. Те же действия производим с зубом второго колеса, проведя окружность О2в из центра О2.
Строим дуги зацепления, для этого через крайние точки рабочего участка профиля зуба проводим нормали к этому профилю (касательные к основной окружности) и находим точки пересечения этих нормалей с начальной окружностью. Полученные точки ограничивают дугу зацепления. Произведя построения для обоих колес получаем точки а/, в/, а// и в//.
4.4 Определение качественных показателей зацепления
Аналитический коэффициент перекрытия определяем по формуле:
![]() (√(75,58452 – 56,381562) + √(163,16452
–
(√(75,58452 – 56,381562) + √(163,16452
–
– 140,953912) – 220,46446 · Sin 26,48o) / 3,14 · 10 · Cos20о = 1,1593
Графический коэффициент перекрытия определяем по формуле:
![]() 34,22 / 3,14 · 10 · 0,939693 = 1,15930
34,22 / 3,14 · 10 · 0,939693 = 1,15930
где ав = ав * µ = 85,56 · 0,4 = 34,22 мм – длина активного участка.
Определение процента расхождения:
![]() (1,15930 – 1,1593) / 1,1593 · 100% = -0,00021%
(1,15930 – 1,1593) / 1,1593 · 100% = -0,00021%
4.5 Определение коэффициентов относительного скольжения
Коэффициенты относительного скольжения определяем по формулам:
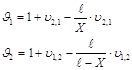
где ![]() = АВ =
256,07 мм – длина теоретической линии зацепления,
= АВ =
256,07 мм – длина теоретической линии зацепления,
![]() 12 / 30 = 0,4
12 / 30 = 0,4
![]() 30 / 12 = 2,5
30 / 12 = 2,5
Х – расстояние от точки А отсчитываемое в направлении к точке В.
Пользуясь формулами, составляем таблицу. Для
этого подсчитываем ряд значений ![]() и
и ![]() , изменяя Х в границах от 0
до
, изменяя Х в границах от 0
до ![]() .
.
Таблица коэффициентов скольжения
| Х | 0 | 15 | 30 | 45 | 60 | AW | 100 | 130 | 160 | 190 | 220 | 245,76 |
|
υ1 |
-∞ | -5,154 | -1,877 | -0,785 | -0,238 | 0,000 | 0,417 | 0,644 | 0,786 | 0,883 | 0,953 | 1 |
|
υ2 |
1 | 0,837 | 0,652 | 0,440 | 0,193 | 0,000 | -0,715 | -1,808 | -3,664 | -7,519 | -20,351 | -∞ |
Из таблицы строим диаграммы в прямоугольной системе координат.
Далее строим круговые диаграммы, проецируя значение Х на активную часть линии зацепления. Из полученных точек, проводим окружности, на которых откладываем соответствующие значения коэффициента скольжения.
4.6 Синтез редуктора с планетарной передачей
Входное звено – Водило Н:
Дано: ![]()
Определить: ![]()
Решение:
Определяем общее передаточное отношение редуктора:
![]()
Определяем передаточное отношение передачи z4 – z5:
![]()
Определяем передаточное отношение планетарной части редуктора:
![]()
Определяем передаточное отношение при неподвижном водиле:

Принимаем: ![]() ,
тогда
,
тогда 
 допустимое значение
допустимое значение ![]()
Определяем соотношение чисел зубьев z1 – z2:

Принимаем ![]() К=2;
3; 4; 5. Берем К=3
К=2;
3; 4; 5. Берем К=3
Определяем числа зубьев шестерен.

Проверка условий:
1. Соосность: ![]() 31+31=34+28
31+31=34+28
Условие выполнено;
2. Сборка: ![]()
![]()
Условие выполнено;
3. Соседство: ![]()
![]()
![]()
![]()
Условие выполнено;
4. Передаточное отношение: 
Условие выполнено.
4.7 Аналитическое определение частот вращения

4.8 Построение картины скоростей
Определяем радиусы делительных окружностей шестерен:

Определение скорости центров колес на водиле
![]()
Выбираем отрезок Р12V12 = 100 мм, при этом µV = 12,14/100 = 0,1214 м/мм.с.
Зная скорость центра водила, равную нулю, и найденную скорость точки строим закономерность скоростей для ведущего звена.
На звене 2,2/ известными точками являются рассмотренная ранее скорость центров колес на водиле и точки касания 1-й и 2-й шестерни равная нулю. Соединив эти точки, получим линию 1,2.
Проецируя скорость точки касания 2/-й и 3-й шестерни на линию 1,2, получаем точку 3. Соединив полученную точку с полюсом, получаем линию 3,4.
Проецируем точку касания 4-й и 5-й шестерни на линию 3,4. найденную точку соединяем с центром 5-й шестерни.
4.9 Построение плана частот вращения
На произвольном расстоянии «Н» от горизонтальной линии выбираем полюс «Р». Через полюс проводим линии параллельные линиям на плане скоростей, которые отсекут отрезки, пропорциональные частотам вращений.
Масштаб плана частот вращения ![]() , тогда:
, тогда:

Расхождения графического и аналитического определения частот вращения составляет менее 3% следовательно, расчеты произведены верно.
5. Синтез кулачкового механизма
5.1 Построение кинематических диаграмм движения выходного звена
5.1.1 Исходные данные
- тип: кулачковый механизм с роликовым толкателем.
- ход толкателя: h=35 мм
- смещение оси толкателя: е =16о
- угол подъема: jп=100о
- угол верхнего выстоя: jпвв=60о
- угол опускания: jо=120о
- эксцентриситет: aдоп=24о
5.1.2 Определение амплитуды ускорения


где: ![]() – фазовые
углы подъема и опускания, рад;
– фазовые
углы подъема и опускания, рад;
![]() – безразмерный коэффициент ускорения.
– безразмерный коэффициент ускорения.
5.1.3 Определение амплитуды скорости


где: ![]() – фазовые
углы подъема и опускания, рад;
– фазовые
углы подъема и опускания, рад;
![]() – безразмерный коэффициент скорости.
– безразмерный коэффициент скорости.
5.1.4 Масштабный коэффициент
![]()
![]()
где: ![]() – длинна
отрезка соответствующая полному обороту кулачка.
– длинна
отрезка соответствующая полному обороту кулачка.
5.2 Определение основных размеров кулачкового механизма
5.2.1 Определение минимального радиуса кулачка
Строим диаграмму зависимости перемещения толкателя от его скорости. К диаграмме проводим касательные лучи t и tI под углом aдоп к оси ординат.
Расстояние между точкой пересечения лучей (О1) и точкой А0 определяет искомый начальный радиус кулачка.
5.2.2 Определение радиуса ролика
Т.к. минимальный начальный радиус кулачка равен 92,58 мм (3-й лист курсового проекта) принимаем начальный радиус rо =95 мм.
rо=r+ rрол;
rрол<0,4 rо;
Принимаем rрол=35 мм, следовательно:
rо=r+ rрол=60+35=95 мм;
35 мм=rрол<0,4 rо=0,4·95=38 мм;
Условия неравенства выполнены.
5.3 Построение профиля кулачка
Строим окружность радиусом rо и в направлении противоположном вращению кулачка и разбиваем полученную окружность на дуги, соответствующие фазовым углам. Первую из этих дуг, разбиваем на 12 равных частей, обозначая точки деления 1,2,3….12, дугу соответствующую фазе опускания делим на 12 равных частей, обозначая точки 13,14,15….25.
По линии действия толкателя от окружности откладываем отрезки с диаграммы перемещений соответственно, полученная кривая даст центровой профиль кулачка.
Конструктивный профиль кулачка получаем как огибающую семейства окружностей радиуса rрол с центрами на центровом профиле кулачка.
На этом работа над курсовым проектом завершена.
Список использованных источников
1. Артоболевский И.И. Теория механизмов и машин. – М.: «Наука», 1975 г.
2. Кореняко А.С. и др. Курсовое проектирование по теории механизмов и машин. – Киев: «Высшая школа», 1970 г.
3. Фролов К.В. Теория механизмов и машин. – М.: «Высшая школа», 1987 г.
4. Попов С.А. Курсовое проектирование по теории механизмов и машин. – М.: «Высшая школа», 1986 г.
5. Методические указания по теме Курсовое проектирование по теории механизмов и машин
