Учебное пособие: Аналитические методы исследования температурных полей
Раздел: Промышленность, производство
Тип: учебное пособие
РЕФЕРАТ
АНАЛИТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ТЕМПЕРАТУРНЫХ ПОЛЕЙ
Дифференциальное уравнение совместно с начальным и граничным условиями полностью определяют задачу, т.е., зная геометрическую форму тела, начальные и граничные условия, можно дифференциальное уравнение решить до конца и, следовательно, найти функцию распределения температуры в любой момент времени. Таким образом, в результате решения должна быть найдена функция
Т (х, у, z, t) == f (х, у, z, t).
Функция f (х, у, z, t) должна удовлетворять дифференциальному уравнению (при подстановке ее вместо Т в дифференциальное уравнение теплопроводности оно должно обращаться в тождество), а также начальному и граничному условиям.
По теореме единственности решения, если некоторая функция Т (х, у, z, t) удовлетворяет дифференциальному уравнению теплопроводности, начальным и граничным условиям, то она является единственным решением данной задачи.
Методы расчета. Для решения задач теплопроводности применяют аналитические методы и численный метод. Аналитические методы состоят в подборе уравнения процесса, удовлетворяющего дифференциальному уравнению теплопроводности и краевым условиям. Из аналитических методов наиболее часто применяются метод Фурье, метод источников и операторный метод. В дальнейшем мы будем применять только метод источников как наиболее простой и удовлетворительно описывающий распределение температуры во многих случаях нагрева металла при сварке.
Метод источников удобен для решения задач нагрева и охлаждения металла при сварке, связанных с местным выделением тепла. Физическая сущность метода источников состоит в том, что любой процесс распространения тепла в теле теплопроводностью можно представить как совокупность процессов выравнивания температуры от множества элементарных источников тепла, распределенных как в пространстве, так и во времени. Решение задач теплопроводности по этому методу в основном сводится к правильному выбору источников и их распределению.
Существующие аналитические методы дают возможность получать решения только для процессов, описываемых линейными дифференциальными уравнениями при линейных граничных условиях, т.е. для тех случаев, когда коэффициенты теплофизических свойств - теплопроводность λ и объемную теплоемкость сγ, а также коэффициент теплоотдачи α можно считать независящими от температуры. Аналитические методы приводят к общим уравнениям процессов, действительным при разнообразных числовых значениях параметров, характеризующих данную задачу, - геометрических размеров, тепловых характеристик режима нагрева и физических свойств металла. В простейших задачах удается получить решение в замкнутой форме, т.е. выразить уравнение процесса через изученные функции от времени, пространственных координат и постоянных параметров процесса. В более сложных задачах решения описываются определенными интегралами или бесконечными рядами.
Для расчета процессов нагрева и охлаждения металла при сварке выбирают постоянные значения коэффициентов λ, су, а и α, соответствующие некоторой средней температуре процесса. В диапазоне температур сварочного процесса - от температуры плавления металла до температуры окружающего воздуха - теплофизические коэффициенты значительно изменяются, особенно коэффициент теплоотдачи. Средняя температура, которой соответствуют принимаемые для расчета значения теплофизических коэффициентов, определяется из сопоставления опытных данных по измерению температуры с результатами расчета. Для расчета температуры при сварке малоуглеродистой стали следует принимать теплофизические коэффициенты металла λ, су и а, соответствующие средней температуре 400-500°, и коэффициент теплоотдачи α, соответствующий температуре 200-400°.
Основные расчетные схемы нагрева металла сварочными источниками
Хотя процессы распространения тепла в условиях сварки являются чрезвычайно сложными, для их решения в ряде случаев удается применять упрощенные методы, сводящие конкретную задачу к идеальным теоретическим схемам.
Так как характер распространения тепла в теле сильно зависит от его формы и размеров, то для расчетов принимают следующие схемы нагреваемого тела.
1. Бесконечное тело – тело (рис.4.1, а), которое имеет такую протяженность по осям oX, oY, oZ, при которой его границы не влияют на характер теплового поля, т.е. его можно заменить бесконечным телом, у которого имеется неограниченная протяженность по всем трем направлениям.
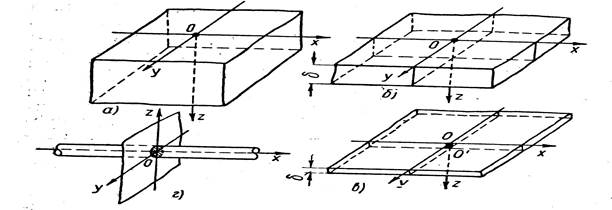
Рис.4.1. Расчетные схемы теплопроводящего тела и источника тепла при нагреве дугой: а - точечный источник О на поверхности полубесконечного тела; б-точечный источник О на поверхности плоского слоя; в - линейный источник О О' в пластине; г - плоский источник О в стержне.
Схема бесконечного тела тем лучше описывает процесс, чем больше размер реального тела, меньше длительность процесса, чем меньше теплопроводность и чем ближе к источнику расположена расчетная область.
Это понятие используется только для предварительных выводов.
2. Полубесконечное тело – тело, имеющее только одну граничную поверхность z = 0, со стороны которой, как правило, действует источник тепла.
3. Пластина - это тело (рис.4.1, в), ограниченное двумя
плоскостями, например, z = 0 и z
= ![]() . При использовании этой
схемы, всегда предполагают, что температура по толщине листа равномерна, а
теплота может распространяться только в плоскости. Схема тем лучше описывает реальное
тело, чем оно тоньше, чем больше продолжительность процесса, чем выше
теплопроводность и чем дальше от источника расположена зона рассчитываемых
температур.
. При использовании этой
схемы, всегда предполагают, что температура по толщине листа равномерна, а
теплота может распространяться только в плоскости. Схема тем лучше описывает реальное
тело, чем оно тоньше, чем больше продолжительность процесса, чем выше
теплопроводность и чем дальше от источника расположена зона рассчитываемых
температур.
4. Плоский слой - это пластина (4.1, б), у которой температура
точек тела по толщине не является равномерной. Эту схему применяют в тех
случаях, когда толщина тела не настолько велика, чтобы можно было пренебречь
влиянием ограничивающей плоскости z =-![]() и считать тело полубесконечным.
и считать тело полубесконечным.
5. Стержень - это тело (рис.4.1, г), имеющее неограниченный размер по одной из координатных осей и ограниченный размер в направлении двух других осей. При использовании этой схемы предполагается, что температура по поперечному сечению стержня распределена равномерно. Тепловой поток в этом случае линеен.
Схемы источника тепла. Схему источника выбирают сообразно со схемой теплопроводящего тела. При наплавке валика на поверхность массивного изделия (или толстого листа) (рис.4.1, а, б) источник считается сосредоточенным в точке О - центре дугового пятна нагрева. При сварке листов встык (рис.4.1, в) целесообразно считать, что тепло дуги приложено к линейному элементу 00', а при сварке встык стержней (рис.4.1, г) или при нагреве торца электрода к плоскому элементу О. Такая схематизация источника не позволяет рассчитывать процесс распространения тепла в области, непосредственно прилегающей к дуге в начальном периоде процесса, т.е. непосредственно после введения тепла дуги. Для этого нужно более точно учитывать характер распределения тепла источника, например, по схемам нормального распределения
Длительность действия источника тепла.
Источники тепла, встречающиеся в практических случаях сварки, также разнообразны. Их схематизируют так:
А) по признаку распределенности: сосредоточенные (точечный, плоский, объемный) и распределенные (по определенному закону ввода тепла в изделие) источники тепла;
Б) по времени действия: мгновенно и непрерывно действующие;
В) по расположению относительно рассматриваемой точки во времени: неподвижные, подвижные, быстродвижущиеся источники тепла.
Фактически тепловой поток сварных источников тепла всегда распределен по нагреваемой поверхности или объему. Однако, учет распределенности ввода тепла от сварочных источников весьма затрудняет получение формул, удобных для расчетов. Поэтому применяют различные упрощенные схемы точечного, линейного, плоского и объемного источников тепла. Эти упрощения в непосредственной близости от источников значительно искажают температурные поля, а на некотором расстоянии от него дают удовлетворяющую практику сходимость с реальными полями.
Точечный источник тепла - это такой источник, объем которого бесконечно мал и в пределе представляет собой точку.
Линейный источник тепла - это такой источник, у которого тепло равномерно распределено вдоль прямой: можно представить, что тепло в этом случае сконцентрировано в цилиндре с r → 0.
Плоский источник тепла - это источник тепла, равномерно распределенный по некоторой плоскости.
Поверхностный источник тепла – это источник, поток тепла которого распределен по поверхности свариваемого тела согласно определенному закону.
Объемный источник тепла - источник, равномерно выделяющий тепло в некотором объеме.
Мгновенный источник тепла - это источник, длительность действия которого стремится к нулю (принимается только для общей исходной схемы).
Непрерывно действующий источник тепла - это источник постоянной тепловой мощности, действующей непрерывно или достаточно длительно.
Неподвижный источник тепла - это не перемещающийся в теле (или по телу) источник тепла постоянной мощности.
Подвижный источник тепла - это источник постоянной мощности, перемещающийся в теле или по поверхности тела прямолинейно с постоянной скоростью.
Быстродвижущийся источник тепла - это подвижный источник тепла, перемещающийся с такой скоростью, при которой распространением тепла перед источником можно пренебречь.
Выбор правильной схемы тела и источника тепла определяет возможность приближения расчета к реальным условиям в соответствующих конкретных случаях.
Рассмотрим некоторые расчетные формулы для различных случаев тепловых процессов, имеющих отношение к тепловым расчетам при сварке.
Начнем с рассмотрения распространения тепла мгновенных источников, сосредоточенных в точке, линии или плоскости в телах различных принятых схем.
Мгновенные сосредоточенные источники
Решения метода источников получаются в наиболее простой форме, если область распространения тепла не ограничена, а источник сосредоточен в весьма малом элементе объема.
Мгновенный точечный источник. В начальный момент времени t = 0 в бесконечно малом элементе объема dx dy dz неограниченного теплопроводящего тела, находящегося при начальной нулевой температуре Т0 = 0, сосредоточено количество тепла Q Дж. Теплофизические свойства тела характеризуются коэффициентом теплопроводности λ [дж/см·сек°С], объемной теплоемкостью сγ [дж1см3·°С] и коэффициентом температуропроводности а [смг/сек] эти коэффициенты остаются постоянными во всем теле за все время процесса и не зависят от температуры. Совместим с элементом объема начало О прямоугольной системы координат XYZ. Тогда процесс распространения тепла мгновенного сосредоточенного источника Q выразится уравнением
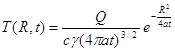 (4.1)
(4.1)
здесь R2 = х2+ y2+ z2 - квадрат расстояния от источника тепла О до точки тела А с координатами х, у, z. Это уравнение процесса является особым решением дифференциального уравнения теплопроводности. Очевидно, что процесс (4.1) симметричен относительно точки О, т.е. температура любой точки тела определяется только ее сферическим радиусом-вектором R. Изотермическими поверхностями являются сферы R = const с центром в точечном источнике О.
Для того, чтобы убедиться, что решение (4.1) удовлетворяет дифференциальному уравнению теплопроводности, вычислим частные производные температуры по времени и пространственным координатам х, у, z и подставим в дифференциальное уравнение. В результате подстановки должно получиться тождество.
Производную ∂Т/∂t, т.е. скорость изменения температуры, найдем по правилу дифференцирования произведения двух функций от t
![]()
где
T=uv; ![]()
![]()
Производную ∂T/∂x, т.е. градиент температуры в направлении ОХ вычислим по правилу дифференцирования сложных функций
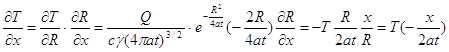 (а)
(а)
Вторую производную температуры по оси ОХ найдем по правилу дифференцирования произведения двух функций
![]() (б)
(б)
Вторые производные по осям OY и OZ выразим аналогично
![]() ;
; ![]() (в)
(в)
Подставляя выражения (а) – (в) в дифференциальное уравнение теплопроводности, получим тождество
![]() (г)
(г)
![]()
![]()
Следовательно, решение (4.1) удовлетворяет дифференциальному уравнению теплопроводности. Необходимо лишь убедиться в правильном выборе постоянного (не зависящего от х и t) сомножителя в выражении (4.1), очевидно, сокращающегося в тождестве (г).
По мере того, как тепло Q источника распространяется по телу, температуры отдельных точек тела изменяются, но общее теплосодержание остается постоянно равным Q. Подсчитаем теплосодержание тела Q(t) в процессе распространения (4.1) тепла точечного источника в любой момент времени t:
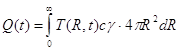 (4.2)
(4.2)
и проверим, остается ли оно постоянно равным Q.
Выражение 4πR2 представляет собой площадь изотермической сферической поверхности радиуса R. Подставим в выражение (4.2) уравнение процесса распространения тепла (4.1) и вычислим интеграл
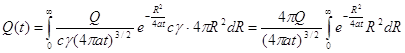
Интеграл берем по частям
∫udp = up - ∫pdv
dp=exp{-R2/4at}·d(-R2/4at) =-exp{-R2/4at}·RdR/2at
p= exp{-R2/4at}; u=-2atR; du=-2atdR
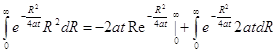
Известно, что 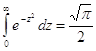 ; приведем к этому виду интеграл
; приведем к этому виду интеграл 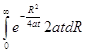 подстановкой
подстановкой ![]() , тогда
, тогда
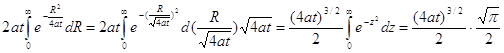
Подставим это значение интеграла в уравнение
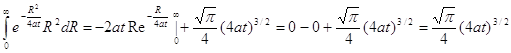
Следовательно,
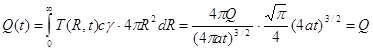
Теплосодержание Q(t) тела, нагретого мгновенным точечным источником, в любой момент процесса t равняется теплу Q, сосредоточенному в начальный момент в точке О, следовательно, постоянный сомножитель в уравнении (4.1) выбран правильно. Теплосодержание бесконечного тела остается постоянным, так как тело не теряет тепла в окружающую среду.
В начальный момент t = 0, формула (4.1) дает бесконечно большую температуру в точке О, T(0,0) → ∞, так как в этот момент конечное количество тепла Q сосредоточено в точке, т.е. в бесконечно малом элементе объема. Во всем объеме тела вне точечного источника начальная температура равна нулю, Т (R, 0) = 0. В весьма удаленных от источника точках тела R→∞ температура во все время процесса остается равной нулю, T(∞,t) → 0.
Изотермические поверхности представляют собой сферы. Убывание
температуры по радиусу выражается множителем ![]() , в то время как множитель
, в то время как множитель ![]() представляет убывание температуры точки R=0 во времени. Наибольшая температура всегда в точке R = 0.
представляет убывание температуры точки R=0 во времени. Наибольшая температура всегда в точке R = 0.
Принцип наложения. В теле действует ряд сосредоточенных источников. Будем полагать коэффициенты λ, су и α независящими от температуры, тогда дифференциальное уравнение теплопроводности и граничные условия становятся линейными. Как известно, сумма любого числа частных решений линейного дифференциального уравнения также удовлетворяет этому уравнению. Поэтому тепло каждого источника распространяется по телу независимо от действия других источников, т.е. так, как и тепло от одиночного источника. Процессы распространения тепла отдельных источников не взаимодействуют между собой, а просто накладываются друг на друга. Принцип наложения состоит в том, что температура в процессе распространения тепла при совместном действии ряда источников рассматривается, как сумма температур от действия каждого из источников в отдельности.
Принцип наложения неприменим, если:
а) коэффициенты теплофизических свойств материала λ, сγ и коэффициент теплоотдачи α считать зависящими от температуры;
б) учитывать происходящие в теле изменения агрегатного состояния, связанные с поглощением или выделением тепла (плавление, отвердевание, структурные превращения).
Если теперь воспользоваться принципом наложения, то, комбинируя мгновенные точечные источники, можем получить множество иных источников теплоты.
Мгновенный линейный источник. Мгновенный линейный источник теплоты представляет собой комбинацию мгновенных точечных источников, действующих одновременно и расположенных по линии.
Температурное поле в пластине от мгновенного линейного источника при отсутствии теплоотдачи получается путем интегрирования температурных полей от мгновенных точечных источников
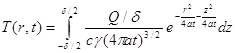 (4.3)
(4.3)
После преобразования и замены Q1=Q/δ, [дж/см] находим
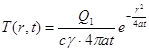 (4.4)
(4.4)
здесь r2 = x2+y2 - квадрат расстояния от источника тепла OZ до точки тела A (x, y, z). Процесс (4.4) симметричен относительно оси OZ, и удовлетворяет дифференциальному уравнению теплопроводности для плоского поля. Температурное поле является плоским, т.е. температура не зависит от координаты z, так как размеры источника в направлении оси OZ неограничены; изотермические поверхности - круговые цилиндры с осью OZ.
Мгновенный плоский источник. Мгновенный плоский источник теплоты представляет собой совокупность мгновенных точечных источников теплоты, действующих одновременно и расположенных в одной плоскости. Под мгновенным плоским источником обычно понимают равномерное распределение Q по сечению.
Температурное поле от мгновенного плоского источника Q2= Q/F, [дж/см2] в стержне без теплоотдачи выражается уравнением
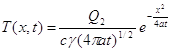 (4.5)
(4.5)
Процесс симметричен относительно плоскости YOZ и удовлетворяет дифференциальному уравнению теплопроводности (4.5) для линейного поля. Так как размеры источника в плоскости YOZ не ограничены, температурное поле является линейным, т.е. температура зависит только от координаты х. Изотермические поверхности-плоскости, параллельные YOZ.
Мгновенный объемный источник теплоты представляет собой совокупность мгновенных точечных источников, распределенных по какому-либо закону в теле. Используя принцип наложения, удается получить различные мгновенные источники, отличающиеся по распределенности. По существу только точечный источник является сосредоточенным по отношению ко всем координатным осям.
Линейный источник является сосредоточенным по отношению к двум координатным осям и распределенным в третьем направлении. Плоский источник является сосредоточенным лишь в одном направлении. Объемный источник может служить примером распределенного источника по всем направлениям.