Курсовая работа: Анализ и оптимизация цифровой системы связи
АНАЛИЗ И ОПТИМИЗАЦИЯ ЦИФРОВОЙ СИСТЕМЫ СВЯЗИ
СОДЕРЖАНИЕ
Введение
1. Методические рекомендации для выполнения анализа и оптимизации цифровой системы связи
1.1 Структурная схема цифровой системы связи
1.2 Определение параметров АЦП и ЦАП
1.3 Выбор вида модуляции и расчет характеристик качества передачи
1.4 Выбор вида помехоустойчивого кода и определение длины кодовой комбинации
1.5 Показатели эффективности цифровой системы связи
Список рекомендованной литературы
Приложение
ВВЕДЕНИЕ
Жизнь современного общества немыслима без широко разветвленных систем передачи информации. Без нее не смогли бы функционировать промышленность сельское хозяйство, транспорт.
Дальнейшее развитие всех сторон деятельности нашего общество немыслимо без широчайшего внедрения автоматизированных систем управления, важнейшей частью которых является система связи для обмена информацией, а также устройства ее хранения и обработки.
Передача, хранение и обработка информации имеют место не только при использовании технических устройств. Обычный разговор представляет собой обмен информацией. Существует множество всевозможных форм представления и хранения информации, такие как: книги, дискеты, винчестеры и т.д.
Технология передачи информации, возможно в большей степени, чем любые другие технологии, оказывает влияние на формирование структуры мирового сообщества. Последние десятилетие сопровождалось революционными изменениями в сети Интернет и вместе с этим радикальными и зачастую непредсказуемыми переменами в способах ведения бизнеса в мировом масштабе. Отсюда следует вполне закономерный вывод, что без знания основ теории передачи сигналов невозможны создание новых совершенных систем связи и их эксплуатация. Поэтому ее изучение является неотъемлемой частью теоретической подготовки студентов.
Передача сообщение из одного пункта в другой составляет основу теории и техники связи. В курсе «Теория электросвязи» изучают единые методы решения разнообразных задач, возникающих при передаче информации от ее источника до получателя.
1. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ДЛЯ ВЫПОЛНЕНИЯ АНАЛИЗА И ОПТИМИЗАЦИИ ЦИФРОВОЙ СИСТЕМЫ СВЯЗИ
1.1 Структурная схема цифровой системы связи
В целом ряде случаев практики возникает проблема передачи непрерывных сообщений дискретным каналом связи. Эта проблема решается при использовании цифровой системы связи. Одной из таких систем есть система передачи непрерывных сообщений методом импульсно-кодовой модуляции (ИКМ) и манипуляции гармоничного носителя. Структурная схема такой системы приведена на рис. 1. Она состоит из источника сообщений (ИС), аналогово-цифрового преобразователя (АЦП), двоичного дискретного канала связи (ДКС), Составной частью которого является непрерывный канал связи (НКС), цифро-аналогового преобразователя (ЦАП) и получателя сообщений (ПС). Каждая из приведенных частей системы содержит в себе еще целый ряд элементов. Остановимся на них подробнее.
Источник сообщений - это некоторый объект или система, информацию о состоянии или поведении которого необходимо передать на некоторое расстояние. Информация, которая передается от ИС, есть непредвиденной для получателя. Поэтому ее количественную меру в теории электросвязи выражают через статистические (вероятностные) характеристики сообщений (сигналов). Сообщение представляет собой физическую форму представления информации. Часто сообщения подают в виде изменяющегося во времени тока или напряжения, которые отображают переданную информацию.
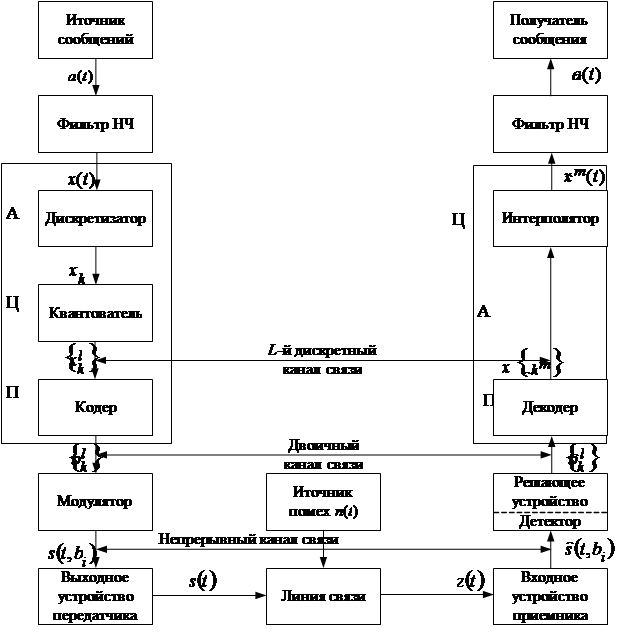
Рисунок 1.1 – Структурная схема цифровой системы связи
В передатчике (ИС) сообщения сначала фильтруется с целью ограничения его спектра некоторой верхней частотой fВ. Это необходимо для эффективного представления отклика ФНЧ x(t) в виде последовательности отсчетов xk = x(kT), k = 0, 1, 2, ..., которые наблюдаются на выходе дискретизатора. Отметим, что фильтрация связана с внесением погрешности eф(t), что отображает ту часть сообщения, которая ослабляется ФНЧ. Дальше отсчеты {хk} квантуются за уровнем. Процесс квантования связан с нелинейным преобразованием непрерывнозначащих отсчетов {хk} в дискретнозначащие {xkl}, которые также привносят погрешность, которую называют погрешностью (шумом) квантования eкв(t). Квантованые уровни {yk = xkl} потом кодируются двоичным безизбыточным (примитивным) или помехоустойчивым кодом.
Последовательность кодовых комбинаций {bkl} образовывает сигнал ИКМ, который направляется к модулятору - устройству, которое предназначенно для согласования источника сообщений с линией связи. Модулятор формирует линейный сигнал S(t, bi), который представляет собой электрическое или электромагнитное колебания, способное распространяться по линии связи и однозначно связанное с сообщением, которое передается, (в данном случае с сигналом ИКМ). Сигнал S(t, bi) создается в результате дискретной модуляции (манипуляции) - процесса изменения одного или нескольких параметров носителя соответственно сигналу ИКМ. При использовании гармоничного носителя UН(t) = Umcos(2pfнt+j0) различают сигналы: амплитудной, частотной и фазовой манипуляций (АМ,ЧМ и ФМ).
Для предотвращения внеполосных излучений в одноканальной связи или при организации многоканального связи, а также для установления нужного отношения сигал/шум на входе приемника линейный сигнал фильтруется и усиливается в выходном каскаде ИС.
Сигнал S(t) с выхода ИС поступает в линию связи, где на него влияет помеха n(t). На входе приемника (Пр) действует смесь z(t) = s(t) + n(t) переданного сигнала и помехи, которая фильтруется во входном каскаде Пр и подается на демодулятор (детектор).
При демодуляции из принятого сигнала ![]() выделяют закон изменения
информационного параметра, который в нашем случае пропорциональный сигналу ИКМ.
При этом для распознавания переданных двоичных сигналов на выход демодулятора
подключается решающее устройство (ВП). При передаче двоичных сигналов bi, i = 0, 1
по ДКC наличие помех в НКC приводит к неоднозначных решений
(погрешностей) РУ, которая в свою очередь вызывает несоответствие переданных и
принятых кодовых комбинаций.
выделяют закон изменения
информационного параметра, который в нашем случае пропорциональный сигналу ИКМ.
При этом для распознавания переданных двоичных сигналов на выход демодулятора
подключается решающее устройство (ВП). При передаче двоичных сигналов bi, i = 0, 1
по ДКC наличие помех в НКC приводит к неоднозначных решений
(погрешностей) РУ, которая в свою очередь вызывает несоответствие переданных и
принятых кодовых комбинаций.
Наконец, для восстановления
переданного непрерывного сообщения a(t), т.е. получение его оценки ![]() , принятые кодовые комбинации
подвергаются декодированию, интерполяции и низкочастотной фильтрации. При этом
в декодере по двоичным кодовым комбинациям восстанавливаются L-е уровни
, принятые кодовые комбинации
подвергаются декодированию, интерполяции и низкочастотной фильтрации. При этом
в декодере по двоичным кодовым комбинациям восстанавливаются L-е уровни ![]() , m = 1 … L-1.
, m = 1 … L-1.
Наличие погрешностей в двоичном ДКC приводит к погрешностям передачи в L-м
ДКС и возникновение шума передачи eП(t). Совокупное действие погрешности фильтрации, шумов
квантования и передачи приводит к неоднозначности между переданным и принятым сообщениями
![]() .
.
1.2 Определение параметров АЦП и ЦАП
Интервал дискретизации по времени Тд выбирается на основе теоремы Котельникова. Обратная к Тд величина - частота дискретизации fд = 1/Tд выбирается из условия
fд ≥ 2Fm, (1.1)
где Fm - максимальная частота первичного сигнала (сообщения).
Увеличение частоты дискретизаций позволяет упростить входной фильтр нижних частот (ФНЧ) АЦП, который ограничивает спектр первичного сигнала, и выходной ФНЧ ЦАП, который восстанавливает непрерывный сигнал по отсчетом. Но увеличение частоты дискретизации приводит к уменьшению продолжительности двоичных символов на выходе АЦП, что требует нежелательного расширения полосы частот канала связи для передачи этих символов. Обычно параметры входного ФНЧ АЦП и выходного ФНЧ ЦАП выбирают одинаковыми.
На рис. 1.2 представлены: S(f) - спектр отсчетов, которые отображаются узкими импульсами, Sa(f) - спектр непрерывного сообщения a(t), A(f) - рабочее ослабление ФНЧ.
Для того, чтобы ФНЧ не вносил линейных искажений в непрерывный сигнал, предельные частоты полос пропуска ФНЧ должны удовлетворять условию
f1 ≥ Fm (1.2)
Для того, чтобы исключить наложение спектров Sa(f) и Sa(f-fД}, а также обеспечить ослабление востанавливающим ФНЧ составных Sa(f-fД} предельные частоты полос задерживания ФНЧ должны удовлетворять условию
f2 ≤ (fД - Fm) (1.3)
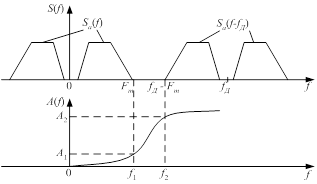
Рисунок 1.2 - Спектр отсчетов и АЧХ ослабления фильтров АЦП и ЦАП
Чтобы ФНЧ не были слишком сложными, отношение предельных частот выбирают из условия
f2 / f1 = 1,3 ... 1,1.(1.4)
После подстановки соотношений (1.2) и (1.3) в (1.4) можно выбрать частоту дискретизации fД.
В системе цифровой передачи методом ИКМ мощность помехи на выходе ЦАП определяется как
![]() ,(1.5)
,(1.5)
где ![]() - средняя мощность шума квантования;
- средняя мощность шума квантования;
![]() - средняя мощность шумов ошибок измерения.
- средняя мощность шумов ошибок измерения.
На практике принято считать, чтобы ![]() не превышало
не превышало ![]() более, чем на 10%, то есть
более, чем на 10%, то есть
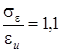
![]() (1.6)
(1.6)
Мощность шума квантования выражается через величину шага квантования Dx:
![]() .(1.7)
.(1.7)
Шаг квантования зависит от числа уровней квантования N:
Dx = Umax / (N-1)(1.8)
Из выражения (1.8) определим минимально возможное число уровней квантования:
![]() (1.9)
(1.9)
Длина двоичного примитивного кода на выходе АЦП есть целое число:
m = log2 N .(1.10)
Поэтому число уровней квантования N выбирается как целая степень числа 2, при котором
N ≥ Nmin.(1.11)
Длительность двоичного символа (бита) на выходе АЦП определяется как
Тб = ТД / m.(1.12)
Среднее количество информации, передаваемое по каналу связи в единицу времени, - скорость передачи информации Ht определим по формуле
![]() ,(1.13)
,(1.13)
где ![]() - скорость передачи отсчетов;
- скорость передачи отсчетов;
![]() – энтропия.
– энтропия.
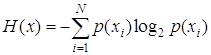 , (1.14)
, (1.14)
где ![]() - закон распределения уровня сигнала,
- закон распределения уровня сигнала, ![]() - число уровней квантования.
- число уровней квантования.
Скорость передачи отсчетов равна частоте дискретизации:
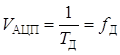 .(1.15)
.(1.15)
1.3 Модуляция
Вид модуляции выбираем так, чтобы скорость передачи информации после модуляции была не меньше производительности источника, т.е.
![]() .
.
![]() ,
,
где ![]() - скорость модуляции,
- скорость модуляции,
![]() - число позиций сигнала.
- число позиций сигнала.
Для АМ, ФМ, ОФМ, КАМ
![]() ,
,
![]() - полоса пропускания канала.
- полоса пропускания канала.
![]()
![]() .
.
Для ОFDМ
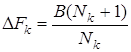 ,
,
где ![]() - число подканалов.
- число подканалов.
тогда 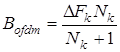 ,
,
После определения числа позиций сигнала М рассчитаем вероятности ошибки
Вероятность ошибки при АМ-М:
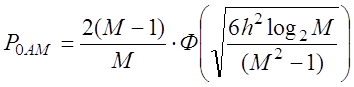 ,
,
Вероятность ошибки при ФМ-М:
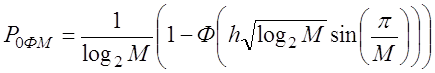
Вероятность ошибки при ОФМ-М:
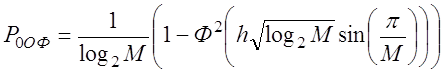
Вероятность ошибки при КАМ-М:
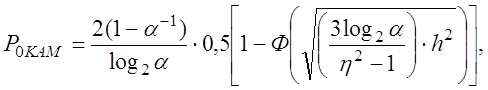
где η – число уровней амплитуды;
α = η+1;
![]() M = 2k, k – четное число.
M = 2k, k – четное число.
Вероятность ошибки при ОFDМ:
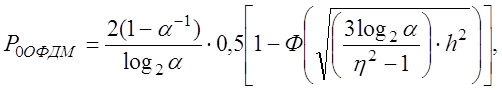
где η – число уровней амплитуды;
α = η+1;
![]() M = 2k, k – четное число.
M = 2k, k – четное число.
Выбор метода модуляции осуществляется в соответствии с критерием минимума вероятности ошибки.
1.4 Выбор вида помехоустойчивого кода и определение длины кодовой комбинации
Помехоустойчивое, или избыточное, кодирование применяется для обнаружения и(или) исправления ошибок, возникающих при передаче по дискретному каналу. Отличительное свойство помехоустойчивого кодирования состоит в том, что избыточность источника, образованного выходом кодера, больше, чем избыточность источника на входе кодера. Помехоустойчивое кодирование используется в различных системах связи, при хранении и передаче данных в сетях ЭВМ, в бытовой и профессиональной аудио- и видеотехнике, основанной на цифровой записи.
Если экономное кодирование сокращает избыточность источника сообщений, то помехоустойчивое кодирование, напротив, состоит в целенаправленном введении избыточности для того, чтобы появилась возможность обнаруживать и(или) исправлять ошибки, возникающие при передаче по каналу связи.
Чтобы посчитать вероятность ошибки кодовой комбинации найдем параметры кода. К ним относятся:
n=m+k – длина кодовой комбинации;
m – число информационных символов(разрядов);
k – число проверочных символов (разрядов);
Особую важность для характеристики корректирующих свойств кода имеет минимальное кодовое расстояние dmin, определяемое при попарном сравнении всех кодовых комбинаций, которое называют расстоянием Хемминга.
В безизбыточном коде все комбинации являются разрешёнными, и, следовательно, его минимальное кодовое расстояние равно единице - dmin = 1. Поэтому достаточно исказиться одному символу, чтобы вместо переданной комбинации была принята другая разрешённая комбинация. Чтобы код обладал корректирующими свойствами, необходимо ввести в него некоторую избыточность, которая обеспечивала бы минимальное расстояние между любыми двумя разрешёнными комбинациями не менее двух - dmin > 2.
Минимальное кодовое расстояние является важнейшей характеристикой помехоустойчивых кодов, указывающей на гарантируемое число обнаруживаемых или исправляемых заданным кодом ошибок.
При применении двоичных кодов учитывают только дискретные искажения, при которых единица переходит в нуль (1 → 0) или нуль переходит в единицу (0 → 1). Переход 1 → 0 или 0 → 1 только в одном элементе кодовой комбинации называют единичной ошибкой (единичным искажением). В общем случае под кратностью ошибки подразумевают число позиций кодовой комбинации, на которых под действием помехи одни символы оказались заменёнными на другие. Возможны двукратные (t = 2) и многократные (t > 2) искажения элементов в кодовой комбинации в пределах 0 < t < n.
Минимальное кодовое расстояние является основным параметром, характеризующим корректирующие способности данного кода. Если код используется только для обнаружения ошибок кратностью t0, то необходимо и достаточно, чтобы минимальное кодовое расстояние было равно
dmin > t0 + 1.(1.29)
В этом случае никакая комбинация из t0 ошибок не может перевести одну разрешённую кодовую комбинацию в другую разрешённую. Таким образом, условие обнаружения всех ошибок кратностью t0 можно записать в виде:
t0 ≤ dmin - 1.(1.30)
Чтобы можно было исправить все ошибки кратностью tи и менее, необходимо иметь минимальное расстояние, удовлетворяющее условию:
![]() .(1.31)
.(1.31)
В этом случае любая кодовая комбинация с числом ошибок tи отличается от каждой разрешённой комбинации не менее чем в tи + 1 позициях. Если условие (1.31) не выполнено, возможен случай, когда ошибки кратности t исказят переданную комбинацию так, что она станет ближе к одной из разрешённых комбинаций, чем к переданной или даже перейдёт в другую разрешённую комбинацию. В соответствии с этим, условие исправления всех ошибок кратностью не более tи можно записать в виде:
tи ≤ (dmin - 1) / 2 .(1.32)
Из (1.29) и (1.31) следует, что если код исправляет все ошибки кратностью tи, то число ошибок, которые он может обнаружить, равно t0 = 2∙tи. Следует отметить, что соотношения (1.29) и (1.31) устанавливают лишь гарантированное минимальное число обнаруживаемых или исправляемых ошибок при заданном dmin и не ограничивают возможность обнаружения ошибок большей кратности. Например, простейший код с проверкой на чётность с dmin = 2 позволяет обнаруживать не только одиночные ошибки, но и любое нечётное число ошибок в пределах t0 < n.
Длина кодовой комбинации n должна быть выбрана таким образом, чтобы обеспечить наибольшую пропускную способность канала связи. При использовании корректирующего кода кодовая комбинация содержит n разрядов, из которых m разрядов являются информационными, а k разрядов – проверочными.
Избыточностью корректирующего кода называют величину
![]() ,(1.33)
,(1.33)
откуда следует
![]() .(1.34)
.(1.34)
Эта величина показывает, какую часть общего числа символов кодовой комбинации составляют информационные символы. В теории кодирования величину Bm называют относительной скоростью кода. Если производительность источника информации равна Ht символов в секунду, то скорость передачи после кодирования этой информации окажется равной
![]() ,(1.35)
,(1.35)
поскольку в закодированной последовательности из каждых n символов только m символов являются информационными.
Если в системе связи используются двоичные сигналы (сигналы типа "1" и "0") и каждый единичный элемент несет не более одного бита информации, то между скоростью передачи информации и скоростью модуляции существует соотношение
![]() ,(1.36)
,(1.36)
где V - скорость передачи информации, бит/с; B - скорость модуляции, Бод.
Очевидно, что чем меньше k, тем больше отношение m/n приближается к 1, тем меньше отличается V от B, т.е. тем выше пропускная способность системы связи.
Извеcтно также, что для циклических кодов с минимальным кодовым расстоянием dmin = 3 справедливо соотношение
k ³ log2(n+1).(1.37)
Видно, что чем больше n , тем ближе отношение m/n к 1. Так, например, при n = 7, k = 3, m = 4, m/n=0,571; при n = 255, k = 8, m = 247, m/n = 0,964; при n = 1023, k = 10, m = 1013, m/n = 0,990.
Приведенное утверждение справедливо и для больших dmin, хотя точных соотношений для связей между m и n нет. Существуют только верхние и нижние оценки, которые устанавливают связь между максимально возможным минимальным расстоянием корректирующего кода и его избыточностью.
Так, граница Плоткина даёт верхнюю границу кодового расстояния dmin при заданном числе разрядов n в кодовой комбинации и числе информационных разрядов m, и для двоичных кодов:
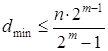 (1.38)
(1.38)
или
![]() при
при ![]() .(1.39)
.(1.39)
Верхняя граница Хемминга устанавливает максимально возможное число разрешённых кодовых комбинаций (2m) любого помехоустойчивого кода при заданных значениях n и dmin:
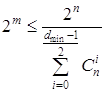 ,(1.40)
,(1.40)
где ![]() -
число сочетаний из n элементов по i элементам.
-
число сочетаний из n элементов по i элементам.
Отсюда можно получить выражение для оценки числа проверочных символов:
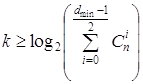 .(1.41)
.(1.41)
Для значений (dmin/n) ≤ 0,3 разница между границей Хемминга и границей Плоткина сравнительно невелика.
Граница Варшамова-Гильберта для больших значений n определяет нижнюю границу для числа проверочных разрядов, необходимого для обеспечения заданного кодового расстояния:
![]() .(1.42)
.(1.42)
Все приведенные выше оценки дают представление о верхней границе числа dmin при фиксированных значениях n и m или оценку снизу числа проверочных символов k при заданных m и dmin.
Из изложенного можно сделать вывод, что с точки зрения внесения постоянной избыточности в кодовую комбинацию выгодно выбирать длинные кодовые комбинации, так как с увеличением n относительная пропускная способность
R = V/B = m/n(1.43)
увеличивается, стремясь к пределу, равному 1.
В реальных каналах связи действуют помехи, приводящие к появлению ошибок в кодовых комбинациях. При обнаружении ошибки декодирующим устройством в системах с РОС производится переспрос группы кодовых комбинаций. Во время переспроса полезная информация не передается, поэтому скорость передачи информации уменьшается.
Можно показать, что в этом случае
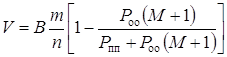 ,(1.44)
,(1.44)
где Poo - вероятность обнаружения ошибки декодером (вероятность переспроса):
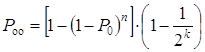 ;(1.45)
;(1.45)
Рпп
- вероятность правильного приема (безошибочного приема) кодовой комбинации ![]() ;
;
М - емкость накопителя передатчика в числе кодовых комбинаций
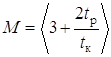 ,(1.46)
,(1.46)
где tp - время распространения сигнала по каналу связи, с;
tк – время передачи кодовой комбинации из n разрядов, с.
Знак < > означает, что при расчете М следует брать большее ближайшее целое значение.
Время распространения сигнала по каналу связи и время передачи кодовой комбинации рассчитываются в соответствии с выражениями
tp = (L/с);
tк = (n/B),
где L - расстояние между оконечными станциями, км;
с - скорость распространения сигнала по каналу связи, км / с (с = 3х105);
В - скорость модуляции, Бод.
При наличии ошибок в канале связи величина R является функцией Р0, n, k, В, L, с. Следовательно, существует оптимальное n (при заданных Р0, В, L, с), при котором относительная пропускная способность будет максимальной.
Для вычисления оптимальных величин n, k, m удобнее всего воспользоваться программным пакетом математического моделирования, таким как MathLab или MathCAD, построив в нем график зависимости R(n). Оптимальное значение будет в том случае, когда R(n) – максимально. При определении величин n, k, m необходимо также обеспечить выполнение условия:
![]() ,(1.47)
,(1.47)
где
![]() - эквивалентная вероятность
ошибки приема единичного разряда при применении помехоустойчивого кодирования с
РОС.
- эквивалентная вероятность
ошибки приема единичного разряда при применении помехоустойчивого кодирования с
РОС.
Величину
![]() можно определить
воспользовавшись соотношением, что при передаче без применения
помехоустойчивого кодирования вероятность ошибочной регистрации кодовой
комбинации Р0кк длины n
равна
можно определить
воспользовавшись соотношением, что при передаче без применения
помехоустойчивого кодирования вероятность ошибочной регистрации кодовой
комбинации Р0кк длины n
равна
![]() .(1.48)
.(1.48)
В тоже время при применении помехоустойчивого кодирования
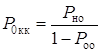 ,(1.49)
,(1.49)
где ![]() - вероятность необнаруженных ошибок
- вероятность необнаруженных ошибок
![]() ;(1.50)
;(1.50)
![]() - вероятность обнаруженных ошибок
- вероятность обнаруженных ошибок
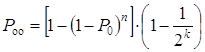 .(1.51)
.(1.51)
Дополнительно к выполнению условия (1.47) необходимо обеспечить
V ³ Ht. (1.52)
Из казанного выше следует, что процесс поиска значений В, n, m, k является итерационным и его удобнее всего оформить в виде таблицы, образец которой приведен в табл. 1.2
Таблица 1.2
| Ht = , Pдоп = . | ||||||
| to | n | m | K |
|
В | V |
| 1 | ||||||
| 2 | ||||||
| 3 | ||||||
| … |
Для обнаружения ошибок выбираем циклический код. Из всех известных помехоустойчивых кодов циклические коды являются наиболее простыми и эффективными. Эти коды могут быть использованы как для обнаружения и исправления независимых ошибок, так и, в особенности, для обнаружения и исправления серийных ошибок. Основное их свойство состоит в том, что каждая кодовая комбинация может быть получена путём циклической перестановкой символов комбинаций, принадлежащей этому же коду.
Циклические коды значительно упрощают
описание линейного кода, поскольку для них вместо задания ![]() элементов двоичной матрицы Ρ требуется задать (n-k+1) двоичных коэффициентов многочлена g(D). Кроме того, они упрощают процедуру кодирования и
декодирования для обнаружения ошибок. Действительно, для осуществления
кодирования достаточно выполнить перемножение полиномов, что реализуется с
помощью линейного регистра, содержащего k ячеек памяти и имеющего обратные связи, соответствующие многочлену
h(D) [4].
элементов двоичной матрицы Ρ требуется задать (n-k+1) двоичных коэффициентов многочлена g(D). Кроме того, они упрощают процедуру кодирования и
декодирования для обнаружения ошибок. Действительно, для осуществления
кодирования достаточно выполнить перемножение полиномов, что реализуется с
помощью линейного регистра, содержащего k ячеек памяти и имеющего обратные связи, соответствующие многочлену
h(D) [4].
Циклический код гарантированно
обнаруживает ошибки кратностью ![]() и исправляет
и исправляет ![]() . Поэтому в системах с решающей обратной связью
применяется кодирование циклическим кодом.
. Поэтому в системах с решающей обратной связью
применяется кодирование циклическим кодом.
При обнаружении ошибки на приемной стороне по обратному каналу связи посылается запрос на блок, в котором она была обнаружена, и тогда этот блок передаётся повторно. Так продолжается до тех пор, пока данный блок не будет принят без обнаруженной ошибки. Такая система называется системой с решающей обратной связью (РОС), поскольку решение о приёме блока или о его повторной передаче производится на приёмной стороне. Система с РОС являются эффективным способом повышения помехоустойчивости передачи информации.
При описании процедуры кодирования и декодирования циклическим кодом удобно использовать математический аппарат, основанный на сопоставлении множества кодовых слов с множеством степенных полиномов. Этот аппарат позволяет выявить для циклического кода более простые операции кодирования и декодирования.
Среди всех полиномов, соответствующих кодовым словам циклического кода, имеется ненулевой полином P(x) наименьшей степени. Этот полином полностью определяет соответствующий код и поэтому называется порождающим.
Степень порождающего полинома P(x) равна n - m, свободный член всегда равен единице.
Порождающий полином является делителем всех полиномов, соответствующих кодовым словам циклического кода.
Нулевая комбинация обязательно принадлежит любому линейному циклическому коду и может быть записана как (xn Å 1) mod (xn Å 1) = 0. Следовательно, порождающий полином Р(x) должен быть делителем бинома xn Å 1.
Это даёт конструктивную возможности построения циклического кода заданной длины n: любой полином, являющийся делителем бинома xn Å 1, можно использовать в качестве порождающего.
При построении циклических кодов, пользуются таблицами разложения биномов xn Å 1 на неприводимые полиномы, т.е. полиномы, которые нельзя представить в виде произведения двух других полиномов (см. приложение А).
Любой неприводимый полином, входящий в разложение бинома xn Å 1, а также любое произведение неприводимых полиномов может быть выбрано в качестве порождающего полинома, что дает соответствующий циклический код.
Для построения систематического циклического кода используется следующее правило построения кодовых слов
![]() ,
,
где R(x) – остаток от деления m(x)×xn-m на Р(x).
Степень R(x), очевидно, меньше (n - m), а потому в кодовом слове первые m, символов будут совпадать с информационными, а последние n - m символов будут проверочными.
В основу процедуры декодирования циклических кодов может быть положено свойство их делимости без остатка на порождающий полином Р(x).
В режиме обнаружения ошибок, если принятая последовательность делится без остатка на Р(x), делается вывод, что ошибки нет или она не обнаруживается. В противном случае комбинация бракуется.
В режиме исправления ошибок декодер вычисляет остаток R(x) от деления принятой последовательности F¢(x) на P(x). Этот остаток называют синдромом. Принятый полином F¢(x) представляет собой сумму по модулю два переданного слова F(x) и вектора ошибок Eош(x):
![]() .
.
Тогда синдром S(x) = F¢(x) mod P(x), так как по определению циклического кода F(x) mod P(x) = 0.
Определенному синдрому S(x) может быть поставлен в соответствие
определенный вектор ошибок Eош(x). Тогда переданное слово F(x) находят,
складывая ![]() .
.
Однако один и тот же синдром может соответствовать 2m различным векторам ошибок. Положим, синдром S1(x) соответствует вектору ошибок E1(x). Но и все векторы ошибок, равные сумме E1(x) Å F(x), где F(x) любое кодовое слово, будут давать тот же синдром. Поэтому, поставив в соответствие синдрому S1(x) вектор ошибок E1(x), мы будем осуществлять правильное декодирование в случае, когда действительно вектор ошибок равен E1(x), во всех остальных 2m- 1 случаях декодирование будет ошибочным.
Для уменьшения вероятности ошибки декодирования из всех возможных векторов ошибок, дающих один и тот же синдром, следует выбирать в качестве исправляемого наиболее вероятный в заданном канале.
Например, для ДСК, в котором вероятность P0 ошибочного приёма двоичного символа много меньше вероятности (1 - P0) правильного приема, вероятность появления векторов ошибок уменьшается с увеличением их веса i. В этом случае следует исправлять в первую очередь вектор ошибок меньшего веса.
Если кодом могут быть исправлены только все векторы ошибок веса i и меньше, то любой вектор ошибки веса от i + 1 до n, будет приводить к ошибочному декодированию.
Вероятность ошибочного декодирования будет равна вероятности Pn(>i) появления векторов ошибок веса i + 1 и больше в заданном канале. Для ДСК эта вероятность будет равна
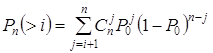 .
.
Общее число различных векторов ошибок, которые может исправлять циклический код, равно числу ненулевых синдромов – 2n-m - 1.
В курсовом проекте необходимо на основании вычисленного в предыдущем пункте значения k выбрать образующий полином по таблице приведенной в приложении А. По выбранному образующему полиному необходимо разработать схему кодера и декодера для случая обнаружения ошибки.
1.5 Показатели эффективности цифровой системы связи
Цифровые системы связи характеризуются качественными показателями, одним из которых является верности (правильность) передачи.
Для оценки эффективности системы
связи вводят коэффициент использования канала связи за мощностью ![]() (энергетическая эффективность) и
коэффициент использования канала по полосе частот
(энергетическая эффективность) и
коэффициент использования канала по полосе частот ![]() (частотная эффективность):
(частотная эффективность):
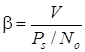 , (1.53)
, (1.53)
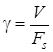 , (1.54)
, (1.54)
где V – скорость передачи информации;
![]() — отношения сигнал/шум на входе демодулятора
— отношения сигнал/шум на входе демодулятора
![]() ; (1.55)
; (1.55)
![]() - ширина полосы частот, которую занимает сигнал
- ширина полосы частот, которую занимает сигнал
![]() , (1.56)
, (1.56)
где М – число позиций сигнала.
Обобщенной характеристикой есть коэффициент использования канала по пропускной способности (информационная эффективность):
![]() . (1.57)
. (1.57)
Для непрерывного канала связи с учетом формулы Шеннона
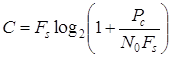
получаем следующее выражение
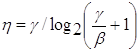 . (1.58)
. (1.58)
Соответственно теоремам Шеннона при h=1 можно получить зависимость между b и g:
b=g/(2g - 1), (1.59)
которая имеет название границы Шеннона, что отображает наилучший обмен между b и g в непрерывном канале. Эту зависимость удобно изобразить в виде кривой на плоскости b - g (рис.1.6).
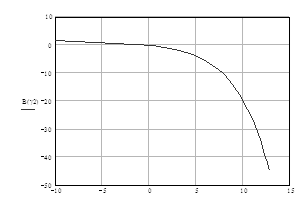
Рисунок 1.6 - Граница Шеннона
Эффективность системы может быть повышена за счет увеличения скорости передачи информации (повышать энтропию сообщений). Энтропия сообщений зависит от закона распределения вероятностей. Следовательно, для повышения эффективности необходимо осуществить перераспределение плотностей элементов сообщения.
Если устранить или ослабить взаимосвязь между элементами сообщений, то также можно добиться повышения эффективности систем.
Наконец, повышения эффективности систем можно получить за счет соответствующего выбора кодирования, обеспечивающего экономию во времени при передачи сообщений.
В курсовом проекте необходимо на построенном графике (рис.1.6) отметить точкой эффективность проектируемой цифровой системы связи.
СПИСОК РЕКОМЕНДОВАННОЙ ЛИТЕРАТУРЫ
1. Методические указания к курсовому проектированию по дисциплине «Теорія електричного зв’язку» Бидный Ю.М., Золотарев В.А., Омельченко А.В. - Харьков: ХНУРЭ, 2008.
2. Омельченко В.А, Санников В.Г. Теория электрической связи. Ч. 1, 2, 3. - К.: ИСДО, 2001.
3. Теория электрической связи: Учебник для вузов / А.Г.Зюко. Д.Д.Кловский, В.И.Коржик, М.В.Назаров; Под ред. Д.Д.Клоковского. – М.: Радио и связь. 1998.
4. Питерсон У., Уэлдон Э. Коды, исправляющие ошибки / Пер, с англ. под ред. Р.Л.Добрушина и С.И.Самойленко. - М-: Мир, 1999. - 596 с.
5. Андреев B.C. Теория нелинейных электрических цепей. Учеб. пособие для вузов. — М.: Радио и связь, 1999. - 280 с.
ПРИЛОЖЕНИЕ
Таблица неприводимых порождающих полиномов степени m
|
Степень m = 7 x7 + x3 + 1 x7 + x4 + x3 + x 2 + 1 x7 + x3 +x 2 + x + 1 |
Степень m = 13 x13 + x4 + x3 + x + 1 x13 + x12 + x6 + x5 + x4 + x3 + 1 x13 + x12 + x8 + x7 + x6 + x5 + 1 |
|
Степень m = 8 x8 + x4 + x 3 + x + 1 x8 + x5 + x 4 + x3 + 1 x8 + x7 + x 5 + x +1 |
Степень m = 14 x14 + x8 + x 6 + x + 1 x14 + x10 + x 6 + 1 x14 + x12 + x6 + x5 + x3 + x + 1 |
|
Степень m = 9 x9 + x4 +x 2 + x + 1 x9 + x5 + x 3 + x2 + 1 x9 + x6 + x 3 + x + 1 |
Степень m = 15 x15 + x10 + x 5 + x + 1 x15 + x11 + x 7 + x6 + x2 + x + 1 x15 + x12 + x3 + x + 1 |
|
Степень m = 10 x10 + x3 + 1 x10 + x4 +x 3 + x + 1 x10+x8+xз+x2+ 1 |
Степень m = 16 x16 + x12 + x 3 + x + 1 x16 + x13 + x12 + x11 + x7 + x 6 + x3 + x + 1 x16 + x15 + x11 + x10 + x9 + x 6 + x2+ x + 1 |
|
Степень m = 11 x11 + x2 + 1 x11 + x7 + x3 + x2 + 1 x11 + x8 + x5 + x2 + 1 |
Степень m = 17 x17 + x3 + x2 + x + 1 x17 + x8 + x7 + x6 + x4 + x3 + 1 x17 + x12 + x6 + x3 + x2 + x + 1 |
|
Степень m = 12 x12 + x4 + x + 1 x12 + x9 + x3 + x2 + 1 x12+ x11 + x6 + x4 + x2 + x+1 |
|