Учебное пособие: Алгоритм решения Диофантовых уравнений
Раздел: Рефераты по математике
Тип: учебное пособие
Алгоритм решения Диофантовых уравнений
Нижнегородская область
Г.Заволжье
2009 г.
В работе рассмотрен метод исследования Диофантовых уравнений и представлены решенные этим методом:
- великая теорема Ферма;
- уравнение Пелля;
- уравнения эллиптических кривых У2=X3+K,
(У2=Х3-Х, У2=Х3-Х+1, У2=Х3+аХ+В);
- иррациональные корни уравнения Х2-У2=1;
- поиск Пифагоровых троек;
- уравнение Каталана;
- уравнение гипотезы Билля
Решение Диофантовых уравнений
Лирическое отступление (ЛО) – 1
Всё началось с теоремы Ферма.
В клубе фермистов оказался случайно, решал совершенно другую задачу, и неожиданно пришла идея ВТФ. Я даже не помнил её классическое написание – хn+уn=сn , формулу ВТФ написал в виде хn = уn + сn, а потом не стал переучиваться, т.к. привык к своему написанию формулы.
ЛО – 2. При доказательстве ссылаюсь на закон распределения простых чисел. Можно было бы обойтись без упоминания оного. Просто сохранил историческую правду, т.к. лично для меня этот закон стал подсказкой.
ЛО – 3. Этот же подход был применён для решения уравнения гипотезы Биля и решения других уравнений. Выводы получились интересными.
Для себя обкатал этот метод на нескольких шуточных уравнениях. При профессиональном подходе, похоже, этот метод может дать как качественные выводы, так и количественные, окончательный же приговор этому методу будет сделан совместными усилиями.
Великая теорема Ферма. Решение
![]() – не имеет решений в целых числах при показателе степени
n>2.
– не имеет решений в целых числах при показателе степени
n>2.
Для доказательства данного утверждения было рассмотрено аналогичное функциональное уравнение. Чтобы получить функциональное уравнение надо обратиться к закону распределения простых чисел в ряду натуральных чисел. В таблице изображена матрица распределения составных чисел в ряду натуральных чисел.
| 4 |
|
6 |
|
8 |
|
10 |
|
12 |
|
14 |
|
16 |
|
18 | … | ||||||
|
+2 |
+3 |
+4 |
+5 |
+6 |
+7 |
+8 |
+9 |
||||||||||||||
| 6 |
|
9 |
|
12 |
|
15 |
|
18 |
|
21 |
|
24 |
|
27 | … | ||||||
|
|
|
||||||||||||||||||||
| 8 |
+4
|
12 | 16 | 20 | 24 | 28 | 32 | 36 | … | ||||||||||||
|
|
|||||||||||||||||||||
| 10 |
|
15 | 20 | 25 | 30 | 35 | 40 | 45 | … | ||||||||||||
|
|
|||||||||||||||||||||
| 12 | +6 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | … | ||||||||||||
|
|
|
||||||||||||||||||||
| 14 |
|
21 | 28 | 35 | 42 | 49 | 56 | 63 | … | ||||||||||||
|
|
|||||||||||||||||||||
| 16 |
|
24 | 32 | 40 | 48 | 56 | 64 | 72 | … | ||||||||||||
|
|
|||||||||||||||||||||
| 18 |
|
27 | 36 | 45 | 54 | 63 | 72 | 81 | … | ||||||||||||
| … | … | … | … | … | … | … | … |
Формула любого составного
числа, соответствующего этой матрице, имеет вид - (![]() i + 1) (
i + 1) (![]() j + 1), где
j + 1), где ![]() i - номер столбца этой матрицы,
i - номер столбца этой матрицы,
![]() j – соответственно, номер строки этой
матрицы. Для верхней строки (
j – соответственно, номер строки этой
матрицы. Для верхней строки (![]() = 1) формула
составного числа примет вид – 2(
= 1) формула
составного числа примет вид – 2(![]() i + 1) – это ряд чётных чисел.
i + 1) – это ряд чётных чисел.
Всё это пока заготовка для доказательства великой теоремы Ферма (ВТФ).
Нечётные числа примут вид
2(![]() i + 1) ± 1. В нашем случае пусть
нечётные числа будут - 2(
i + 1) ± 1. В нашем случае пусть
нечётные числа будут - 2(![]() i + 1) - 1.
i + 1) - 1.
Чтобы доказать ВТФ надо рассмотреть три варианта:
- I X - чётное число, У - чётное число, Z - чётное число;
- II X - чётное число, У - нечётное число, Z - нечётное число;
- III X - нечётное число, У - чётное число, Z - нечётное число.
Вариант I. Пусть уравнение ВТФ верно для чётных чисел.
В формулу ВТФ вставим аналитические выражения чётных чисел.
[2(![]() 1 + 1)]n = [2(
1 + 1)]n = [2(![]() 2 + 1)]n + [2(
2 + 1)]n + [2(![]() 3 + 1)]n ,
3 + 1)]n ,
где для определённости
возьмём ![]() 1 >
1 > ![]() 2 >
2 > ![]() 3
3
После упрощения.
(![]() 1 + 1)n = (
1 + 1)n = (![]() 2 + 1)n + (
2 + 1)n + (![]() 3 + 1)n
3 + 1)n
По сути, природа этого
уравнения та же, что и уравнения ВТФ, т.к. зависимость между Х, У, Z и столбцами
матрицы ![]() i – функции соответствующие линейным
уравнениям.
i – функции соответствующие линейным
уравнениям.
Можно составить систему подобных уравнений.
![]()
![]()
![]()
………………………………………… (а)
![]()
![]()
Каждое уравнение этой системы также является функциональным уравнением ВТФ.
Для обоснования данного утверждения рассмотрим следующий пример.
Вычислим несколько значений
![]() соответствующих числу 10 по
формуле чётных чисел.
соответствующих числу 10 по
формуле чётных чисел.
2(![]() 1 + 1)=10
1 + 1)=10 ![]() 1 =4
1 =4
2(![]() 2 + 2)=10
2 + 2)=10 ![]() 2 =3
2 =3
2(![]() 3 + 3)=10
3 + 3)=10 ![]() 3 =2
3 =2
Т.е. переменная ![]() может принимать значения от 1 до ¥.
может принимать значения от 1 до ¥.
Условием для существования системы уравнений (а) служат лишь условия
![]() и
и ![]() .
.
Данные условия слабее условий существования пифагоровых троек, где, если (а, в, с) – пифагорова тройка, то таковою будет и тройка (nа, nв, nс), при всех n = 1, 2, 3 …
Т.е. система (а) должна
быть справедливой для всего ряда натуральных чисел, при условии неизменности
величин р и f, и условии ![]() 3
+1<½K½<¥.
3
+1<½K½<¥.
Это следует при
предположении справедливости уравнения ВТФ – ![]() .
.
У системы уравнений (а) есть 2 варианта:
- I - каждое уравнение системы имеет решение;
- II - каждое из уравнений системы не имеет решений.
Если взять в уравнении
системы к = -![]() 3,
тогда уравнение примет
вид
3,
тогда уравнение примет
вид
![]()
Данное уравнение вида ![]() не может иметь
решений в целых числах при n>2.
не может иметь
решений в целых числах при n>2.
Тогда не верно любое уравнение системы и следовательно не верно и уравнение ВТФ.
Рассматривались чётные значения Х, У, Z.
В системе уравнений (а) переменные
![]() I принимают значения всех чисел натурального ряда, и
чётных и не чётных. Тогда ВТФ тоже доказана для всего ряда натуральных чисел.
Если же рассматривать варианты II и III доказательства ВТФ, тогда
функциональные уравнения примут вид:
I принимают значения всех чисел натурального ряда, и
чётных и не чётных. Тогда ВТФ тоже доказана для всего ряда натуральных чисел.
Если же рассматривать варианты II и III доказательства ВТФ, тогда
функциональные уравнения примут вид:
II [2(![]() 1+1)]n=[2(
1+1)]n=[2(![]() 2+1)-1]n+[2(
2+1)-1]n+[2(![]() 3+1)-1]n
3+1)-1]n
III [2(![]() 1+1)-1]n=[2(
1+1)-1]n=[2(![]() 2+1)]n+[2(
2+1)]n+[2(![]() 3+1)-1]n
3+1)-1]n
Принципиально в доказательстве ВТФ это ничего не меняет.
Для обоснования данного, довольно – таки экзотического на сегодняшний день метода, далее будут рассмотрены некоторые известные задачи.
Уравнение Пелля
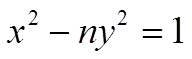 (1)
(1)
Рассмотрим 3 варианта:
- I Х - чётное число, У - нечётное число, n - нечётное число;
- II Х - нечётное число, У - нечётное число, n - чётное число;
- III Х - нечётное число, У - чётное число, n – любое, и чётное, и нечётное число.
И всегда ½Х½ > ½У½
Вариант I.
Составим функциональное уравнение.
![]() , где, конечно же,
, где, конечно же, ![]() 1 >
1 > ![]() 2
2
Возьмём к = - ![]() 2, тогда
2, тогда
![]()
После преобразований
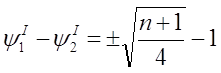 (2)
(2)
где 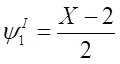 ;
; 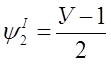 .
.
Окончательно, после подстановки будет
![]() , где n = 3, 15 . . . . .
, где n = 3, 15 . . . . .
Проверим при n = 3
а) ![]() ,
, ![]()
б) ![]() ,
, ![]()
Подставим (а) в уравнение (1)
![]()
![]()
![]()
![]()
![]()
![]()
Для случая Х = 2, У = 1, n = 3 будет
![]()
Подставим (б) в уравнение (1)
![]()
![]()
![]()
![]()
Для ![]()
![]()
Проверка даёт
![]()
Для ![]()
![]()
Проверка даёт
![]()
Составим последующее функциональное уравнение.
![]()
После упрощения
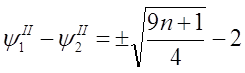
где 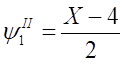 ,
, 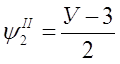
После подстановки
![]()
Следующее функциональное уравнение примет вид
![]()
После упрощения
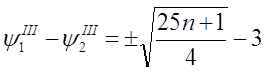
где 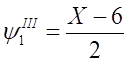 ,
, 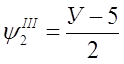
После подстановки
![]()
Получилась система бесконечных решений:
![]()
![]()
![]()
![]() (3)
(3)
![]()
Вариант II.
Функциональное уравнение примет вид.
![]()
![]()
После преобразований будет
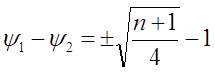 , где n чётные числа n = 8, 24 ……
, где n чётные числа n = 8, 24 ……
Само же выражение идентично формуле (2).
Система бесконечных решений примет вид системы (3).
Тогда система решений (3) будет общей для вариантов I и II при n – чётных и нечётных числах.
Вариант III.
Также напишем функциональное уравнение.
![]()
Опускаю все вычисления, - напишу окончательный результат:
![]()
![]()
![]()
![]()
![]()
На решении данного уравнения Пелля подтверждено следующее утверждение из доказательства ВТФ:
Или все формулы системы функциональных уравнений имеют решения, или же в системе уравнений нет ни одной такой формулы.
Мне не приходилось встречать классического решения этого уравнения, - для меня это чистый экспромт. Специалисты могут сравнить.
Вообще же, этим методом решается любое уравнение вида:
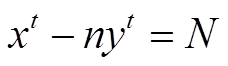 ,
,
а уравнение Пелля лишь как частный случай, при t = 2 и N = 1.
Уравнение
![]() . (1)
. (1)
(У2=Х3-Х, У2=Х3-Х+1, У2=Х3+аХ+В)
Рассмотрим 4 варианта:
- I У - нечётное число, Х - нечётное число, К - чётное число;
- II У - нечётное число, Х - чётное число, К - нечётное число;
- III У - чётное число, Х - чётное число, К - чётное число;
- IV У - чётное число, Х - нечётное число, К - нечётное число.
Решение этого уравнения принципиально ни чем не отличается от решения уравнения Пелля, - в обоих уравнениях наличие двух переменных.
Вариант I.
![]()
Во всех четырёх вариантах
У>Х, и следовательно ![]() 1>
1>![]() 2
2
![]()
![]()
![]()
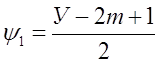
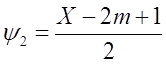
Тогда будет
![]() (2)
(2)
Получилась система уравнений (1) и (2).
Хотя и без решения системы часть решений уже можно определить.
![]()
![]()
![]()
Рассмотрим частный случай уравнения (2) при m=1.
![]() ,при m≥1.
,при m≥1.
Т.к. K чётное число, тогда K=8, 24, 48, 80, 120, 168, 224, 288, 360 ….
Получится возрастающий ряд K.
Этому ряду K соответствует ряд разностей:
У-Х=2, 4, 6, 8, 10, 12 …. при положительных значениях радикала и
У-Х=-4, -6, -8, -10, -12 …. при отрицательных значениях радикала.
Рассмотрим четыре примера, взяв соответственно:
1) У-Х=2 K=8
2) У-Х=4 K=24
3) У-Х=6 K=48
4) У-Х=8 K=80
1) У=Х+2, подставим в уравнение (1) при K=8
![]()
![]()
Х1=1 Х2=2 Х3=-2
У1=3 У2=4 У3=0
K=8 K=8 K=8
2) У=Х+4
Х=1
У=5
K=24
3) У=Х+6
Х=1
У=7
K=48
4) У=Х+8
Х1=1 Х2=4 Х3=-4
У1=9 У2=12 У3=4
K=80 K=80 K=80
Вариант II.
![]()
![]()
![]() (3)
(3)
![]()
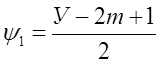
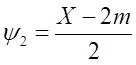
Подставляем в (3), получаем
![]() , m≥1.
, m≥1.
При m=1 K примет значения –7, 1, 17, 41, 73, 113 ….;
Как и в предыдущем варианте получится возрастающий ряд K, и ему соответствует ряд разностей:
У-Х=-1, 1, 3, 5, 7, 9….; У-Х=-3, -5, -7, -9….
Вариант III.
![]()
![]()
![]()
![]()
![]()
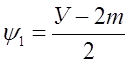
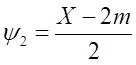
После подстановки ![]() 1,
1, ![]() 2, окончательно получим
2, окончательно получим
![]() , m≥1.
, m≥1.
При m=1 K примет значения –4, 8, 28, 56 ….
Этому ряду K соответствует ряд разностей:
У-Х=0, 2, 4, 6….; У-Х=-4, -6, -8, -10….
Вариант IV.
![]()
![]()
![]()
![]()
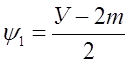
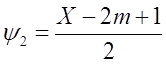
![]() , m≥1.
, m≥1.
При m=1 K примет значения 3, 15, 35, 63, 99 ….
Этому ряду K соответствует ряд разностей:
У-Х=1, 3, 5, 7, 9 ….; У-Х=-3, -5, -7, -9, -11….
Уравнения У2=Х3-Х, У2=Х3-Х+1, У2=Х3+аХ+В и прочие уравнения эллиптических кривых познавательного интереса для данного алгоритма не представляют.
Повторяясь, скажу, важно лишь количество неизвестных. Поэтому распишу лишь первое из них.
- I У - чётное число, Х - нечётное число;
- II У - чётное число, Х - чётное число, всегда У > Х, и как следствие ![]() 1>
1>![]() 2.
2.
Вариант I.
![]()
![]()
![]()
Т.к.
![]()
![]()
![]()
Тогда
![]()
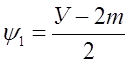
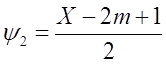
После подстановки
![]()
Вариант II.
Сразу пишу ответ
![]()
И после всех преобразований и подстановок
![]()
Работа при исследовании уравнений данным алгоритмом достаточно монотонная.
Исследование уравнения ![]() проведено, кстати, не до конца.
проведено, кстати, не до конца.
Не рассмотрена ситуация У < Х.
Иррациональные корни уравнения
![]() .
.
Известно, что данное уравнение имеет иррациональные корни. Но для решения, предположим, что уравнение увидели впервые. И тогда начало решения будет традиционным для данного алгоритма.
Рассмотрим 2 варианта:
- I Х - чётное число, У - нечётное число;
- II Х - нечётное число, У - чётное число.
Всегда Х > У
Вариант I.
Функциональное уравнение общего вида будет:
![]() , где
, где ![]() ,
, ![]() (1)
(1)
Преобразования изображу подробно
![]()
![]()
![]() (2)
(2)
В уравнении (1) ![]() ,
, ![]()
Тогда  ,
, 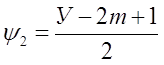
Значения ![]() и
и ![]() подставим в формулу (2)
подставим в формулу (2)
![]()
Исходное уравнение
![]()
запишем в виде
![]()
Тогда
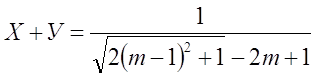
До конца не преобразуя, оставляю решение в виде системы
|
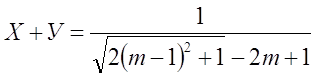
Вариант II.
![]() , где
, где ![]() ,
, ![]() (4)
(4)
Преобразования без комментариев.
![]()
![]()
![]() (5)
(5)
В уравнении (4)
![]()
![]()
Тогда 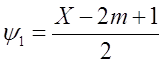 ,
, 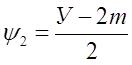
Значения ![]() и
и ![]() подставим в формулу (5)
подставим в формулу (5)
И сразу пишу систему решений
![]()
![]()
|
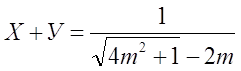
Итого: иррациональными решениями уравнения
![]()
являются две системы уравнений (3) и (6).
Отрицательные значения радикалов не рассматриваю.
Поиск Пифагоровых троек
![]() (1)
(1)
Пусть Х – нечётное число, У – чётное число, Z – нечётное число
и Х > У > Z.
![]()
![]() ,
,
уравнение ![]() представлено в виде
представлено в виде ![]() , и далее оно расписано в виде произведения
, и далее оно расписано в виде произведения ![]() (2)
(2)
![]()
Можно составить три системы уравнений:
|
![]()
|
![]()
![]()
|
![]()
И по порядку начинаем рассматривать все три варианта.
Заранее составим заготовку для их решения.
![]()
![]()
![]()
![]()
Откуда следует
![]()
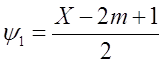
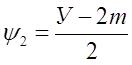 (3)
(3)
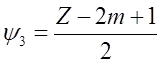
|
![]()
Произведя подстановку соотношений (3) и с учётом уравнений (2) получим систему из трёх уравнений с тремя же неизвестными.
![]()
![]()
![]()
![]()
После соответствующих преобразований будет
![]()
![]()
Перед радикалом убран знак «минус» ибо комплексные решения не интересуют.
Простой перебор значений m даёт следующие результаты:
- при m=2 ![]() , тогда
, тогда ![]()
![]()
- при m=7 ![]() , тогда
, тогда ![]()
![]()
б) Система (б) после сокращений примет вид
![]()
![]()
![]()
После подстановок (3) и с учётом уравнения (2) получим систему уравнений:
![]()
![]()
![]()
![]()
![]()
откуда
![]()
При m≥1, Z =1, 3, 5, 7, 9, 11…. т.е. все нечётные числа, хотя единицу надо убрать, ибо она не удовлетворяет условию системы (4).
Из (Х-У)(Х+У)=Z2 получаем, систему уравнений
![]()
![]() (4)
(4)
![]()
Решая данную систему, получаем ряд значений Пифагоровых троек.
| Х | 5 | 13 | 25 | 41 | 61 | 85 | 113 | 145 | 181 | 221 | 265 | 313 | 365 | 421 |
| У | 4 | 12 | 24 | 40 | 60 | 84 | 112 | 144 | 180 | 220 | 264 | 312 | 364 | 420 |
| Z | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | 25 | 27 | 29 |
В этой таблице, когда Z является простым числом, дальнейшие расчёты Пифагоровых троек отсутствуют.
Когда Z является составным числом, возможен дальнейший расчёт.
Возьмём Z=15 Z2=225
225=1х 225; 3х75; 5х45; 9х25
Будем рассматривать систему (4), подставляя подчёркнутые произведения .
![]()
![]() Х=39, У=36, Z=15, после сокращения на три
Х=39, У=36, Z=15, после сокращения на три
![]() Х=13, У=12, Z=5
Х=13, У=12, Z=5
![]()
![]() Х=25, У=20, Z=15, после сокращения на пять
Х=25, У=20, Z=15, после сокращения на пять
![]() Х=5, У=4, Z=3
Х=5, У=4, Z=3
![]()
![]() Х=17, У=8, Z=15, несколько неожиданный
Х=17, У=8, Z=15, несколько неожиданный
![]() результат, ибо рассматривается по условию У >
Z.
результат, ибо рассматривается по условию У >
Z.
Возьмём Z=27 Z2=729
729=1х729; 3х243; 9х81
Расчёт показывает
Х=123, У=120, Z=27, после сокращения на три Х=41, У=40, Z=9;
Х=45, У=36, Z=27, после сокращения на девять Х=5, У=4, Z=3.
Возьмём Z=35 Z2=1225
1225 = 1х1225; 5х245; 7х175; 25х49.
Х = 125 (25), 91 (13), 37
У = 120 (24), 84 (12), 12
Z = 35 (7), 35 (5), 35
И последний раз в качестве примера
Возьмём Z=39 Z2=1521
1521=1х1521; 3х507; 9х169; 13х117.
Х = 255 (85), 89, 65
У = 252 (84), 80, 52
Z = 39 (13), 39, 39
К сожалению системы пока не вижу.
в) После преобразований получается:
![]()
![]()
![]()
![]()
И формула для Z.
![]()
Рассмотрим следующий вариант.
От вышеуказанного он отличается следующим условием: У < Z,
а следовательно и ![]() <
< ![]() .
.
![]()
![]()
![]()
![]()
![]()
Получается девять систем уравнений.
|
![]()
|
![]()
|
![]()
|
![]()
|
![]()
|
![]()
|
![]()
|
![]()
|
![]()
И после подстановки в эти
девять систем значений ![]()
из соотношений (3), получается также девять систем значений Х, У, Z.
|
![]()
![]()
|
![]()
![]()
|
![]()
![]()
|
![]()
![]()
|
![]()
![]()
|
![]()
![]()
|
![]()
![]()
|
![]()
![]()
|
![]()
![]()
И далее, - все девять систем надо решить.
г) ![]()
- нет решения в целых числах при любых m.
д) ![]()
е) ![]() , при m=2, У=8;
, при m=2, У=8;
Решим уравнение (X-Z)(X+Z)=64 перебором произведений
64=1х64; 2х32; 4х16.
Из соотношения 2х32, получаем
![]()
![]()
![]()
т.е.
![]()
![]()
![]()
![]()
Система
![]()
![]()
![]()
Даёт значения
![]()
![]()
![]()
![]()
ж) ![]() - нет корней в целых числах.
- нет корней в целых числах.
з) ![]() , при m=2, У=12 и т.д.
, при m=2, У=12 и т.д.
Разберём до конца У=12 и соответственно У2=144.
Число 144 даёт следующие интересующие нас произведения
144=2х72; 4х36; 6х24; 8х18.
Из формулы (Х-Z)(X+Z)=У2 получим следующие значения Х, У, Z.
| Х 37 | 20 (5) | 15 (5) | 13 |
| У 12 | 12 (3) | 12 (4) | 12 |
| Z 35 | 16 (4) | 9 (3) | 5 |
и) ![]() - нет корней в целых числах.
- нет корней в целых числах.
к) ![]() - нет корней в целых числах.
- нет корней в целых числах.
л) ![]() - нет корней в целых числах.
- нет корней в целых числах.
м) ![]() - нет корней в целых числах.
- нет корней в целых числах.
Рассмотрим следующий вариант:
- пусть все три числа
чётные и Х>У>Z, как и ![]() >
> ![]() >
> ![]() .
.
Заранее знаю, что после сокращения всех членов на 22 уравнение перейдёт в область всех натуральных чисел.
![]()
![]()
![]()
![]()
![]()
Из последнего уравнения составим три системы уравнений, после соответствующих преобразований, используя соотношения
![]()
![]()
![]()
![]()
![]()
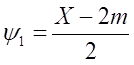
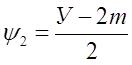
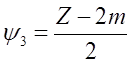
![]()
![]()
![]()
![]()
![]()
|
![]()
![]()
|
![]()
![]()
Рассмотрим все три полученные системы уравнений (н), (п), (р).
н) ![]() и преобразуя – Z=2m, получились все чётные числа при m ≥1.
и преобразуя – Z=2m, получились все чётные числа при m ≥1.
В таблице приведены значения троек для m ≤10, при условии Х-У=2.
| Х | 5 | 10 | 26 | 37 | 50 | 65 | 82 | 101 | ||
| У | 3 | 8 | 24 | 35 | 48 | 63 | 80 | 99 | ||
| Z | 4 | 6 | 10 | 12 | 14 | 16 | 18 | 20 |
п) ![]() - то же выражение, что и в (н).
- то же выражение, что и в (н).
р) ![]()
После упрощения.
![]()
При m=2, 3 значения троек будут
| Х 13 | 34 (17) | ||
| У 5 | 16 (8) | ||
| Z 12 | 30 (15) |
При рассмотрении вопроса о Пифагоровых тройках не было целью составление таблиц этих троек. Ибо целью этой статьи является показ возможностей алгоритма решения Диофантовых уравнений.
Решение уравнения Каталана
![]()
Уравнение данного вида получается при попытке решения гипотезы Биля. Поэтому решение данного уравнения является как бы леммой гипотезы Биля. Ответ будет дан лишь в качественной оценке. Количественный анализ принципиально не труден, но нуден.
Рассмотрим 2 варианта:
- I А - чётное число, В - нечётное число;
- II А - нечётное число, В - чётное число.
Каждый из вариантов распадается опять же на два случая:
А > В, Х < У;
А < В, Х > У.
И требуется перебрать комбинации Х, У – чётные - нечётные числа.
Итого 16 вариантов. Плюс варианты гипотезы Биля.
И если всё это обилие решать количественно, - это уже приличная работа для издания отдельной брошюры, а не публикации в формате статьи.
Вариант I.
1. А > В, Х < У Х – чётное число, У – чётное число.
Основания и показатели расписываю за один заход.
![]() , где конечно же
, где конечно же ![]() 1>
1>![]() 2,
а
2,
а ![]() 1 <
1 < ![]() 2.
2.
Вначале разбираемся с показателями
![]()
На второй стадии пройдусь по основаниям
![]()
![]()
Равенство левой и правой части уравнения невозможно.
Тогда и исходное
уравнение ![]() решений не имеет.
решений не имеет.
2. А > В, Х < У Х – нечётное число, У – нечётное число.
![]()
Во всех решениях вначале степень, затем основание
![]()
![]()
![]()
Решим полученное условие относительно А и В.
![]()
![]()
![]()
![]()
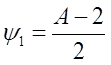
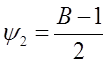
После подстановки А=В+1.
Т.е., чтобы уравнение Ах-Ву=1 существовало при заданных условиях д.б. А=В+1.
3. А > В, Х < У Х – чётное число, У – нечётное число.
![]()
После преобразований
![]()
![]()
Далее вывод, как и в примере (1).
4. А > В, Х < У Х – нечётное число, У – чётное число.
![]()
![]()
![]()
Результат, как и в примере (2).
5. А < В, Х > У Х – чётное число, У – чётное число.
![]()
![]()
Нет решения, ибо это формула разности квадратов.
6. А < В, Х > У Х – нечётное число, У – нечётное число.
![]()
![]()
![]()
![]()
Решение у такой формулы возможно.
7. А < В, Х > У Х – чётное число, У – нечётное число.
![]()
![]()
![]()
Противоречий для существования данной формулы нет.
8. А < В, Х > У Х – нечётное число, У – чётное число.
![]()
![]()
И окончательно.
![]()
Запрета на существование такого уравнения не вижу, но дальнейший анализ не в этой статье.
Вариант II.
9. А > В, Х < У Х – чётное число, У – чётное число.
![]()
![]()
Уравнение разности квадратов - тогда решений не существует.
10. А > В, Х < У Х – нечётное число, У – нечётное число.
![]()
![]()
![]()
Уравнение реальное - тогда решение есть.
11. А > В, Х < У Х – чётное число, У – нечётное число.
![]()
![]()
Уравнение реальное.
Пример: 32-23=1
12. А > В, Х < У Х – нечётное число, У – чётное число.
![]()
![]()
Решение существует.
13. А < В, Х > У Х – чётное число, У – чётное число.
![]()
![]()
14. А < В, Х > У Х – нечётное число, У – нечётное число.
![]()
![]()
15. А < В, Х > У Х – чётное число, У – нечётное число.
![]()
![]()
16. А < В, Х > У Х – нечётное число, У – чётное число.
![]()
![]() (а)
(а)
Для случаев 13, 14, 15, 16 итоговое уравнение одинаковое.
Рассмотрим эти четыре случая чуть подробнее.
![]()
![]() , тогда
, тогда
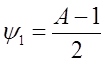
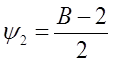
После подставим в уравнение (а) получим
![]() , при начальном условии
, при начальном условии ![]() .
.
Тогда варианты 13, 14, 15, 16 – не верны.
Из рассмотренных выше задач, при всех вариантах начальных условий, - 8 задач решений в целых числах не имеют.
Для закрепления материала предлагаю рассмотреть два заведомо не имеющих решения уравнения.
Первый пример.
Пусть: А - чётное число.
В - нечётное число.
А > В, Х > У, Х – чётное число, У – нечётное число.
Основное противоречие состоит в условии А > В, Х > У.
![]()
![]() ,
,
что, конечно же, не возможно, т.к. левая часть всегда больше правой.
Второй пример.
Пусть: А - нечётное число.
В - чётное число.
А > В, Х > У, Х – чётное число, У – нечётное число.
![]()
После соответствующих преобразований
![]() ,
,
что, конечно же, не возможно.
Гипотеза Биля (ГБ).
![]() , где А, В, С –
взаимно простые числа и Х, У, Z > 2.
, где А, В, С –
взаимно простые числа и Х, У, Z > 2.
Рассмотрим 2 варианта:
- I А - чётное число, В - нечётное число, С - нечётное число;
- II А - нечётное число, В - чётное число, С - нечётное число.
Строго говоря, чтобы полностью разобрать ГБ, надо рассмотреть все варианты решения уравнений.
Но дело в том, что новый метод исследования диофантовых уравнений говорит о том, что ГБ не верна, т.е. уравнение при некоторых сочетаниях А, В, С, Х, У, Z может иметь место. По этому будет рассмотрено лишь два примера, которые указывают на возможность решения уравнения.
Вариант I.
а) Пусть А > В > С, и Х < У < Z, и А - чётное число, В - нечётное число, С - нечётное число.
Составим функциональное уравнение.
![]()
Подразумевая систему
функциональных уравнений, возьмём к = - ![]() 3
3
![]() (1)
(1)
Возьмём обозначение ![]()
![]()
Уравнение (1) примет вид уравнения Каталана ![]()
И именно из этого и следует наличие решений у уравнения ГБ.
Вариант II.
а) Пусть А > В > С, и Х < У < Z, где Х, У – нечётные числа, А - нечётное число, В - чётное число, С - нечётное число.
Составим функциональное уравнение.
![]()
Решая относительно
основания, получим ![]()
Проведу преобразование в показателях
![]()
После упрощения.
![]()
Вполне реальное уравнение, которое должно иметь место.
В настоящей работе представлен сравнительно небольшой анализ. Более серьёзным анализом займусь в зиму 2009-2010 годов.
И приведу один контр пример.
Заведомо противоречивое начальное условие – в примере (а) пусть
Х > У > Z.
Тогда в уравнении Каталана
![]() ,
, ![]()
И тогда не может иметь место знак равенства.
Т.е. задача с заведомо неверными начальными условиями исключается сразу.
Вот почему и есть основание верить в решения в целых числах у уравнения ГБ.
Заключение
Данному алгоритму на момент появления в интернете всего два месяца. Дитё.
Что можно нарешать за два месяца? А больше я себе не могу позволить заниматься не профилирующим предметом в моей трудовой деятельности.
Напоследок хочу коснуться одной практической проблемы при решении Диофантовых уравнений данным методом.
Сколько раз можно «бить» по уравнению, представленным алгоритмом?
Можно по отношению к конкретному уравнению теоретически на единицу меньше, чем число неизвестных в данном уравнении.
Первая стадия – убираем самое меньшее неизвестное. А на второй стадии уже надо знать разницу между оставшимся самым маленьким числом, и предстоящим. Или же не зная этой разницы, вводить параметр.
Почему это происходит?
На первой стадии мы наши неизвестные приблизим к началу числовой оси. Если самое наименьшее число чётное, то оно будет находиться на позиции «два», а если не чётное – то на позиции «один».
И чтобы ещё по уравнению пройтись представленным алгоритмом, надо все неизвестные «откатить» от начала числовой оси на несколько шагов. Приведу простейший пример.
Пусть есть уравнение Х3+У3+Z3=6903
И пусть каким - то одним нам известным способом мы узнаём, что Х, У, Z – нечётные и следуют подряд.
![]()
![]()
Сдвигаю неизвестные на «шаг» от начала оси.
![]()
![]()
![]()
![]()
![]()
У=2m+1, при m=6 У=13
Z=2m-1, при m=6 Z=11
![]()
при m=6 Х=15
Данный метод позволяет данные вычисления.
Часть 2
Подход к решению уравнений
![]() (1)
(1)
![]() (2)
(2)
Сейчас данные уравнения, насколько мне известно, решены для n=4.
Т.е. доказано наличие для каждого из уравнений бесконечного количества сочетаний натуральных чисел a, b, c, d удовлетворяющим условиям равенств уравнений (1), (2).
Причём доказательства основаны на компьютерном поиске данных чисел. Нашли компьютерным расчётом для n=4, отлично - теперь сделайте тоже самое для n=5 и т.д., т.к. даже для n=1000 в целом проблема не будет закрыта.
Мне кажется, что есть общий подход к доказательству утверждения о существовании равенств в уравнениях (1), (2) при любых n ® ¥.
Я сомневаюсь, что мои рассуждения сойдут за доказательства, но направление, может быть, окажется верным.
I. ![]()
Существует наличие сочетаний a, b, c, d на чётность и нечётность.
Разберу одну возможность, - пусть все числа a, b, c, d будут чётными.
А далее буду использовать алгоритм решения Диофантовых уравнений.
Составлю систему уравнений. Бумагу экономить не буду, - распишу подробно.
![]()
![]()
![]()
![]()
![]()
![]()
В этих уравнениях пусть ![]() 1 >
1 > ![]() 3 >
3 > ![]() 4 >
4 >
![]() 2
– очевидное предположение.
2
– очевидное предположение.
Произведу в уравнениях
системы сокращения на 2n
и члены с ![]() 2 перенесу в
правую часть уравнений, а члены с
2 перенесу в
правую часть уравнений, а члены с ![]() 3 – в левую.
3 – в левую.
Сокращением же на 2n от чётных значений a, b, c, d уравнения системы переведены в значения всего натурального ряда.
![]()
![]()
![]()
![]()
![]()
![]()
Далее используются формулы разности степеней.
![]()
![]() +…..+
+…..+![]() =
=![]()
![]() +…..+
+…..+![]()
![]()
![]()
![]() +…..+
+…..+![]() =
=![]()
![]() +…..+
+…..+![]()
![]()
![]() +…..+
+…..+![]() =
=![]()
![]() +…..+
+…..+![]()
![]()
![]() +…..+
+…..+![]() =
=![]()
![]() +…..+
+…..+![]()
![]()
![]() +…..+
+…..+![]() =
=![]()
![]() +…..+
+…..+![]()
Т.к. ![]() ,
,![]() , система (4) примет вид:
, система (4) примет вид:
![]() p
p![]() +…..+
+…..+![]() =f
=f![]() +…..+
+…..+![]()
p![]() +…..+
+…..+![]() = f
= f![]() +…..+
+…..+![]()
p![]() +…..+
+…..+![]() = f
= f ![]() +…..+
+…..+![]()
p![]() +…..+
+…..+![]() = f
= f![]() +…..+
+…..+![]()
p![]() +…..+
+…..+![]() = f
= f![]() +…..+
+…..+![]()
Т.е. у каждого уравнения начальной системы уравнений (3) произведено понижение формы.
Ну и конечно же доказательство надо вести не от n к n-1, а наоборот, - от n=2 поэтапно к n ® ¥.
Уравнение (2) доказывается аналогичным образом.
![]() и т.д.
и т.д.
Мне в вышеизложенное и самому не на все 100% верится.
Поэтому я взываю к коллективному разуму.
Главное сомнение же вот в чём:
В таком разе все уравнения с нечётным числом членов решений в натуральных числах не будут иметь, ну или не так строго, могут не иметь.
Т.к. нет понижения формы у одного из членов уравнения.
Как, например, у уравнения (2) бесконечное число сочетаний натуральных чисел a, b, c, d существует, тогда, как у уравнения
![]() таких сочетаний может и не быть.
таких сочетаний может и не быть.
И без компьютерного расчёта, хотя бы для n=3, не обойтись, и если взять мои утверждения, и очень убедительные контрдоводы кого-либо другого.