Реферат: Анализ алгоритма Евклида в Евклидовых кольцах
Раздел: Рефераты по математике
Тип: реферат
ОТДЕЛ ОБРАЗОВАНИЯ ГОМЕЛЬСКОГО ГОРОДСКОГО
ИСПОЛНИТЕЛЬНОГО КОМИТЕТА
Государственное учреждение образования
«Средняя общеобразовательная школа №22 г.Гомеля»
Конкурсная работа
«Анализ алгоритма Евклида в Евклидовых кольцах»
Ученицы 9Б класса
ГУО СОШ№22 г. Гомеля
Самсоновой Галины Викторовны
Научный руководитель –
Горский Сергей Михайлович,
учитель математики
Государственного учреждения
образования СОШ №22 г. Гомеля
Гомель, 2009
Содержание
Введение
1 Алгоритм Евклида
1.1 Применение алгоритма Евклида
1.2 Математическая проблема календаря
2 Анализ алгоритма Евклида
3 Евклидовы кольца
4 Аналоги чисел Фибоначчи
Заключение
Список использованных источников
Введение
Один из героев великого французского писателя Мольера, месье Журден, был страшно удивлён, узнав, что всю жизнь пользуется прозой. Мы с вами, тоже можем удивляться, узнав, что всю жизнь мы исполняем огромное число всякого рода алгоритмов.
В каждодневной жизни человеку приходится решать большое число разного рода задач, в широком смысле этого слова, не только математических или физических, которые требуют применения определённых алгоритмов.
Когда мы переходим улицу на регулируемом светофором перекрёстке, мы выполняем определённый алгоритм, когда же переходим улицу в месте, не регулируемом светофором, выполняем другой алгоритм (эти алгоритмы заданы правилами уличного движения). Когда приготавливаем чай, пользуемся определённым алгоритмом (иногда заданным инструкцией, напечатанной на упаковке). И когда мы берём книги в библиотеке, мы выполняем определённые правила пользования библиотечными книгами, т.е. тоже определенный алгоритм.
Разве можно перечислить все задачи, при решении которых мы используем определённые алгоритмы?
Слово алгоритм стало широко употребляться в последнее время. Оно означает описание совокупности действий, составляющих некоторый процесс. Обычно здесь подразумевают процесс решения некоторой задачи, но и кулинарный рецепт, и инструкция по пользованию стиральной машиной, и описание процедуры проявления фотоплёнки, и ещё многие другие правила, не имеющие отношения к математике, являются алгоритмами.
Термин « алгоритм» произошёл от имени учёного VIII - IХ веков Аль–Хорезми. Его имя говорит, что родился он в городе Хорезми, который сейчас входит в состав Узбекистана. Большую часть своей жизни Аль-Хорезми провёл при дворе багдадских халифов. Из математических работ Аль-Хорезми до нас дошли всего две - алгебраическая и арифметическая. От названия первой книги родилось слово АЛГЕБРА.
Первые строки второй книги были переведены так: «Сказал Алгоритми. Воздадим хвалу Бог, нашему вождю и защитнику». Так имя Аль-Хорезми перешло в Алгоритми, откуда и появилось слово «алгоритм».
В своей работе я поставила цель исследовать известное в математике понятие «Алгоритм Евклида». В связи с этим были поставлены следующие задачи:
1. Изучить алгоритм Евклида.
2. Рассмотреть применение алгоритма Евклида для нахождения НОД чисел и многочленов.
3. Установить связь с числами Фибоначчи.
4. Найти аналоги чисел Фибоначчи в иных Евклидовых кольцах
1 Алгоритм Евклида
Одним из древнейших математических алгоритмов является алгоритм Евклида для нахождения наибольшего общего делителя двух положительных чисел. Вот его простейший вид. Пусть заданы два целых числа. Если они равны, то их наибольшим делителем будет каждое из них. В этом случае процесс заканчивается на первом шаге. Если они не равны, то вычитаем из большего числа меньшее. Это шаг алгоритма. Теперь рассмотрим вычитаемое и разность. Проделаем с ними ту же самую процедуру. Этот процесс будет продолжаться до тех пор, пока вычитаемое и разность не станут равны. Поскольку большее число в парах на каждом шаге уменьшается, но всегда не меньше единицы, то такой процесс не может продолжаться бесконечно, а закончится через несколько шагов.
Определение
Число d Î Z , делящее одновременно числа а , b , c , ... , k Î Z, называется общим делителем этих чисел. Наибольшее d с таким свойством называется наибольшим общим делителем. Обозначение:
d = ( a , b , c , ..., k )
Теорема. Если (a , b) = d , то найдутся такие целые числа u и v , что
d = au + bv .
Определение. Целые числа a и b называются взаимно простыми, если
(a , b ) = 1.
Вспоминая свойство 1 из предыдущего пункта, легко заметить, что два числа a и b являются взаимно простыми тогда и только тогда, когда найдутся целые числа u и v такие, что au + bv = 1.
Пусть даны два числа a и b ; a ³ 0, b ³ 0, считаем, что a > b . Символом := в записи алгоритма обозначаем присваивание. Алгоритм:
1. Ввести a и b .
2. Если b = 0 , то Ответ: а . Конец .
3. Заменить r := "остаток от деления а на b ", а := b , b := r .
4. Идти на 2.
В современной буквенной записи, алгоритм Евклида выглядит так:
a > b; a, b Î Z .
|
a = bq 1 + r 1 |
0 £ r 1 < b |
|
r n -3 = r n -2 q n -1 + r n -1 |
0 £ r n -1 < r n -2 |
Имеем: b > r 1 > r 2 >... > r n > 0, следовательно процесс оборвется максимум через b шагов.
1.1 Применение алгоритма Евклида
Как и всякая добротно выполненная работа, алгоритм Евклида дает гораздо больше, чем от него первоначально ожидалось получить. Из его разглядывания ясно, например, что совокупность делителей а и b совпадает с совокупностью делителей (a, b). Еще он дает практический способ нахождения чисел u и v из Z (или, если угодно, из теоремы пункта 2) таких, что
r n = au + bv = (a, b).
Действительно, из цепочки равенств имеем:
r n = r n -2 - r n -1 q n = r n -2 - (r n -3 - r n -2 q n -1) q n =...
(идем по цепочке равенств снизу вверх, выражая из каждого следующего равенства остаток и подставляя его в получившееся уже к этому моменту выражение)
... = au + bv = (a, b).
Несомненно, описанная Евклидом процедура определения общей меры двух величин применительно к числам (а общая мера двух натуральных чисел, очевидно, есть их наибольший общий делитель) была изобретена задолго до Евклида. Таким же образом находили НОД и древние китайские математики. И только то, что эта процедура стала известна в эпоху Возрождения именно из «Начал, дало ей название « алгоритм Евклида»
Скорее всего, она возникла из коммерческой практики древних купцов, когда им надо было сравнивать различные отношения целых чисел. Как, например, сравнивать отношения чисел 3703700 и 1234567 и чисел 22962965 и 7654321? Вполне естественна была попытка узнать, сколько раз меньшее число укладывается в большем. Легко проверить, что 3703700 = 2 · 1234567 + 1234566, а 22962965 = 3 · 7654321 + 2. Ясно теперь, что отношение 3703700 к 1234567 меньше, чем отношение 22962965 к 7654321. Таким образом, что сейчас мы записываем как
![]() = 2,99999919 <
= 2,99999919 <![]() = 3, 000000261,
= 3, 000000261,
Древние вычислители объясняли длинной фразой.
Если бы
пришлось сравнить более близкие отношения чисел, например, ![]() и
и ![]() , то вычисления были бы более сложными:
, то вычисления были бы более сложными:
71755875 = 61735500 + 10020375;
61735500 = 6 · 10020375 + 1613250;
10020375 = 6 · 1613250 + 340875;
1613250 = 4 · 340875 + 249750;
340875 = 249750 + 91125;
249750 = 2 · 91125 + 67500;
91125 = 67500 + 23625;
67500 = 2 · 23625 + 20250;
23625 = 20250 + 3375;
20250 = 6 · 3375.
Алгоритм Евклида здесь позволяет определить НОД чисел 71755875 и 61735500, равный 3375 и соответствует разложению отношения 71755875 к 61735500 в цепную дробь:
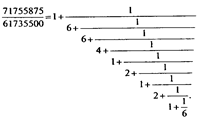
Алгоритм Евклида оказывается эквивалентным современной процедуре разложения числа в цепную дробь и более того, позволяет «округлить» отношения чисел, т.е. заменять дробь с большим знаменателем на очень близкую к ней дробь с меньшим знаменателем. В самом деле, выражение
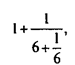 |
равное дроби ![]() , в современной математике называется «подходящей дробью»
разложения отношения α=
, в современной математике называется «подходящей дробью»
разложения отношения α=![]() в цепную (или непрерывную) дробь.
в цепную (или непрерывную) дробь.
Ясно, что
α=1+![]() < 1 +
< 1 +![]() и α=1 +
и α=1 +![]() > 1+
> 1+ ![]() =
= ![]() ,
,
поскольку
6+ ![]() >6+
>6+![]() .
.
Приведенное
сравнение ![]() >
>![]() было выполнено в III в. до н.э. Аристархом
Самосским в трактате «О расстоянии и размерах Луны и Солнца».
было выполнено в III в. до н.э. Аристархом
Самосским в трактате «О расстоянии и размерах Луны и Солнца».
Сейчас известно, что подходящие дроби разложения любого (рационального или иррационального) числа в цепную дробь представляют собой наилучшие рациональные приближения этого числа.
1.2 Математическая проблема календаря
Григорий XIII не был математиком. Он был римским папой, но его имя связано с важной математической задачей – проблемой календаря.
Природа дала нам две естественные единицы времени: год и сутки (солнечные). как сказано в одном старом учебнике космографии, «к сожалению, год не равен целому числу суток». С этим нельзя не согласиться, так как из упомянутого факта проистекает много неудобств. Зато он порождает интересную математическую проблему.
1
 |
год = 365 суток 5 часов 48 минут 46 секунд=365,2421199 суток.
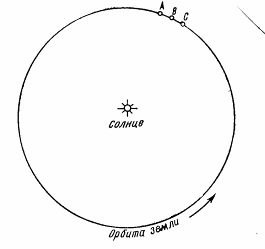
Узаконить в гражданской жизни такую длину года невозможно. А что получится, если принять гражданский год равным ровно 365 суткам? На рис. показана орбита Земля. 1 января 1980 года в 0 часов Земля находилась в точке А. за 365 суток она не дойдёт до точки А и 1 января 1981 года в 0 часов окажется в точке В, а 1 января 1982 года – в точке С и т.д. Получится, что если отмечать положение Земли на орбите, соответствующие фиксированной дате, то оно будет каждый год иное: оно будет отставать почти на 6 часов. За 4 года отставание состоит почти сутки, и фиксированная дата будет попадать на разные времена года, т.е. 1 января с зимы постепенно переместится на осень, потом на лето.
Выход из этого положения есть. Надо считать, что в некоторых годах по 365 суток, а в некоторых – по 366, чередуя годы так, чтобы средняя длина года была возможно ближе к истинной. Так можно воспроизвести истинную длину года с любой точностью, но для этого может понадобиться очень сложный закон чередования коротких (простых) и длинных (високосных) годов, что нежелательно. Нужен компромисс: сравнительно простой закон чередования коротких и длинных годов, дающий среднюю длину года, достаточно близкую к истиной.
Эту задачу впервые решил Юлий Цезарь. Точнее говоря, это сделал по его поручению александрийский астроном Созиген, вызванный для этой цели в Рим. Юлий Цезарь ввёл такую систему: три года подряд коротких (простых), четвёртый – длинный (високосный). Много позже, когда было принято христианское летосчисление, високосными стали считать годы, номера которых делятся на 4.
Этот календарь
называется юлианским. В России он существовал до февраля 1918 года. По юлианскому
календарю средняя длина года равна 365 ![]() суток = 365 суток 6 часов.
суток = 365 суток 6 часов.
Как видно, средняя длина юлианского года больше истинной на 11 минут 14 секунд.
Юлианский календарь был улучшен папой Григорием Х111. В 1582 году он произвёл следующую реформу календаря. Сохранил чередование простых и високосных лет, но добавил правило: если номер года оканчивается двумя нулями, а число сотен не делится на 4, то этот год простой, но 1600 - високосный. Кроме того, считая. Что от начала летосчисления (от «рождества Христова») уже накопилась ошибка в 10 дней, Григорий Х111 сразу прибавил 10 дней. С тех пор накопилось ещё 3 дня (в 1700,1800, 1900 годах). Поэтому в настоящее время расхождение между юлианским и новым (григорианским) составляет 13 дней.
Какова средняя
длина григорианского года? Из 400 лет по юлианскому календарю – 100 високосных.
А по григорианскому – 97. Поэтому средняя длина григорианского года = 365![]() суток = 365,242500 суток = 365 суток 5 часов 49 минут 12 секунд,
т.е. она больше истинной на 26 секунд.
суток = 365,242500 суток = 365 суток 5 часов 49 минут 12 секунд,
т.е. она больше истинной на 26 секунд.
Как видим, весьма простыми средствами достигнута очень большая точность. Как получили этот результат?
Сначала подумаем, как мы сами решили бы проблему чередования високосных лет. Мы представили бы длину года в виде цепной дроби
1год=365 суток 5 часов 48 минут 46 секунд = [365; 4, 7, 1, 3, 5, 64] суток.
Примечание 1. π – иррациональное число. Оно выражается бесконечной цепной дробью. Величина года – эмпирическая. Всякая эмпирическая величина измеряется лишь с определённой точностью, и говорить об её рациональности или иррациональности не имеет смысла. Приведённая выше величина года - принятая, и мы должны считать её точной. Она выражается конечной цепной дробью.
Примечание 2. Чтобы выразить длину года в виде цепной дроби, незачем выражать её десятичной дробью в долях суток (аналогично тому, как мы делали с числом π). Это вычисление производится так (целая часть отброшена):

Находим несколько первых подходящих дробей. Целую часть опустим, так как наличие в каждом году 365 целых суток не требует напоминаний:

Каждый
столбец дает решение проблемы календаря. Например, первый столбец дает для
длины года приближенное значение 365![]() суток. Чтобы реализовать такую длину года, надо считать
високосным 1 год из 4. Вообще, третья строка дает величину цикла или периода, а
вторая – число високосных лет в цикле. Например, второй столбец соответствует
такому решению: 7 високосных лет из каждых 29. Средняя длина года при этом
получится 365
суток. Чтобы реализовать такую длину года, надо считать
високосным 1 год из 4. Вообще, третья строка дает величину цикла или периода, а
вторая – число високосных лет в цикле. Например, второй столбец соответствует
такому решению: 7 високосных лет из каждых 29. Средняя длина года при этом
получится 365![]() суток. Это точнее, чем 365
суток. Это точнее, чем 365![]() , но зато сложнее.
, но зато сложнее.
2. Анализ алгоритма Евклида
Прежде чем, приступить к анализу алгоритма Евклида рассмотрим числа Фибоначчи.
Суть последовательности Фибоначчи в том, что начиная с 1,1 следующее число получается сложением двух предыдущих.
1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 ….
Приступим к анализу алгоритма Евклида. Нас будет интересовать наихудший случай — когда алгоритм работает особенно долго? Спросим точнее: какие два наименьших числа надо засунуть в алгоритм Евклида, чтобы он работал в точности заданное число шагов? Ответ на этот вопрос дает
Теорема (Ламэ, 1845 г.). Пусть n Î N , и пусть a > b > 0 такие, что алгоритму Евклида для обработки а и b необходимо выполнить точно n шагов (делений с остатком), причем а - наименьшее с таким свойством. Тогда а = F n +2 , b = F n +1 , где F k — k- ое число Фибоначчи.
Следствие. Если натуральные числа a и b не превосходят N Î N , то число шагов (операций деления с остатком), необходимых алгоритму Евклида для обработки a и b не превышает
é log Ф ( Ö 5 N ) ù - 2,
где é a ù - верхнее целое a , F = (1 + Ö 5)/2 — больший корень характеристического уравнения последовательности Фибоначчи.
log Ф ( Ö 5 N ) » 4,785 · lg N + 1,672, поэтому, например, с любой парой чисел, меньших миллиона, алгоритм Евклида разбирается не более, чем за é 4,785 · 6 + 1,672 ù - 3 = 31 - 3 = 28 шагов.
3. Евклидовы кольца
Неформально, евклидово кольцо — в абстрактной алгебре — кольцо, в котором «работает» алгоритм Евклида.
Примеры
·
Кольцо
целых чисел Z. Пример евклидовой функции — абсолютное значение ![]() .
.
· Кольцо целых гауссовых чисел Z[i] (где i — мнимая единица, i2 = − 1) с нормой d(a + ib) = a2 + b2 — евклидово.
· Произвольное поле K является евклидовым кольцом с нормой, равной 1 для всех элементов, кроме 0.
· Кольцо многочленов в одной переменной K[x] над полем K. Пример евклидовой функции — степень deg.
· Кольцо формальных степенных рядов K[[x]] над полем K является евклидовым кольцом. Норма степенного ряда — номер первого ненулевого коэффициента в нём (для нулевого ряда норма равна минус бесконечности).
· Евклидовыми являются кольца конечных двоичных и конечных десятичных дробей, так как они являются кольцами частных кольца целых чисел Z.
· Евклидовыми являются кольца рациональных функций над полем C с фиксированными полюсами, так как такие кольца являются кольцами частных кольца многочленов C[x].
4 Аналоги чисел Фибоначчи
Мною были построены аналоги чисел Фибоначчи в кольце многочленов и исследованы некоторые их свойства. Для этих целей я использовала программу Mathematica 5.1.
Определение аналогов чисел Фибоначчи:
![]() ;
; ![]() ;
; ![]()
Первые 10 многочленов:
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]()
6. ![]()
7.
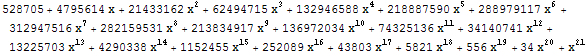 |
8.
9.
 |
10.

Заключение
Данная работа посвящена расширенному алгоритму Евклида. Алгоритму Евклида более 2000 лет и он традиционно используется для нахождения наибольшего общего делителя натуральных чисел посредством остатков от деления.
Со временем алгоритм Евклида стали применять и в диафантовом анализе (для решения уравнений в целых числах), и в механизме цепных дробей (для наилучшего приближения действительных чисел рациональными), используется и для быстрого возведения в степень в компьютерных алгоритмах, и в криптографии.
Как было показано, числа Фибоначчи обладают экстремальным свойствам: при подстановке в алгоритм Евклида чисел Фибоначчи с номерами n и n+1, алгоритм выполняется за n шагов.
В своей работе я нашла многочлены обладающие теми же свойствами. В дальнейшем я планирую исследовать свойства этих многочленов и построить степенные ряды, обладающие теми же свойствами.
Список использованных источников
1. С. Ленг, Алгебра, М., 1968
2. С. Коунтинхо, Введение в теорию чисел. Алгоритм RSA, – М. 2001
3. Н.М. Бескин, Замечательные дроби, –М.,1980 г.
4. А.И. Кострикин, Введение в алгебру, – М., 2000
5. Энциклопедия для детей Аванта + «математика» том 11 2002 г.
6. О. Зарисский, Коммутативная алгебра, т.1.,– М., 1963
7. Л.Я. Куликов, Алгебра и теория чисел – М.,1979 г.
8. А.Г. Цыпкин, Справочник по математике для средних учебных заведений, – 1984 г.
9. А.П. Савин, Я познаю мир. Сер. «Математика» / А.П. Савин, В.В. Станцо, А.Ю. Котова, – М. 2006 г.