Контрольная работа: Анализ поведения функций при заданных значениях аргумента
Национальный Горный Университет Украины
Контрольная работа
по дисциплине
«Использование вычислительной техники»
Днепропетровск
Используя приложение Excel пакета Microsoft Office (версии 95,97, 2000 или XP) рассчитать значения функций и построить графики.
Оформить работу в текстовом редакторе Microsoft Word (все выражения должны быть набраны в редакторе формул Microsoft Equation).
Задание 1. Исследовать методами математического анализа поведение функций при заданных значениях аргумента
Алгебраические рациональные ![]()
1. Область существования: ![]()
2. Четность: ![]() функция ни четная, ни нечетная
функция ни четная, ни нечетная
3. Точки разрыва: ![]() . Промежутки
непрерывности
. Промежутки
непрерывности ![]()
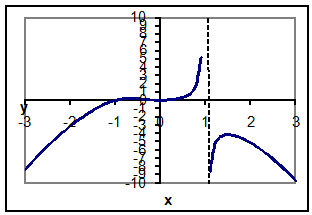
4. Точки пересечения функции с осями координат: (-1,0), (0,0).
5. Экстремум функции ![]()
![]()
![]()
![]()
![]()
![]()
![]()
| x |
|
-0,67 | (-0,67; 0) | 0 | (0,1) | (1;1,5) | 1,5 |
(1,5;+ |
|
y/ |
+ | 0 | – | 0 | + | + | 0 | – |
| y | возрастает | 0,23 | убывает | 0 | возрастает | возрастает | -4,14 | убывает |
6. Вертикальная асимптота ![]()
Значения функции ![]()
| x | y | x | y |
| -3 | -8,35714 | 0,1 | 0,01002 |
| -2,9 | -7,74751 | 0,2 | 0,040645 |
| -2,8 | -7,15684 | 0,3 | 0,094995 |
| -2,7 | -6,58507 | 0,4 | 0,18188 |
| -2,6 | -6,03218 | 0,5 | 0,321429 |
| -2,5 | -5,49812 | 0,6 | 0,558367 |
| -2,4 | -4,98288 | 0,7 | 1,001629 |
| -2,3 | -4,48648 | 0,8 | 1,982951 |
| -2,2 | -4,00896 | 0,9 | 5,16786 |
| -2,1 | -3,55043 | 1 | |
| -2 | -3,11111 | 1,1 | -8,52118 |
| -1,9 | -2,69131 | 1,2 | -5,39604 |
| -1,8 | -2,29152 | 1,3 | -4,51373 |
| -1,7 | -1,91249 | 1,4 | -4,20771 |
| -1,6 | -1,55529 | 1,5 | -4,14474 |
| -1,5 | -1,22143 | 1,6 | -4,21375 |
| -1,4 | -0,91299 | 1,7 | -4,36713 |
| -1,3 | -0,63276 | 1,8 | -4,58106 |
| -1,2 | -0,38428 | 1,9 | -4,84229 |
| -1,1 | -0,17182 | 2 | -5,14286 |
| -1 | 0 | 2,1 | -5,47767 |
| -0,9 | 0,126958 | 2,2 | -5,84332 |
| -0,8 | 0,206561 | 2,3 | -6,23743 |
| -0,7 | 0,23971 | 2,4 | -6,65832 |
| -0,6 | 0,232105 | 2,5 | -7,1047 |
| -0,5 | 0,194444 | 2,6 | -7,57564 |
| -0,4 | 0,140752 | 2,7 | -8,07039 |
| -0,3 | 0,085268 | 2,8 | -8,58838 |
| -0,2 | 0,039365 | 2,9 | -9,12914 |
| -0,1 | 0,00998 | 3 | -9,69231 |
График функции ![]()
Алгебраические иррациональные ![]()
1. Область существования: ![]()
2. Четность: ![]() функция ни четная, ни нечетная
функция ни четная, ни нечетная
3. Функция непрерывна
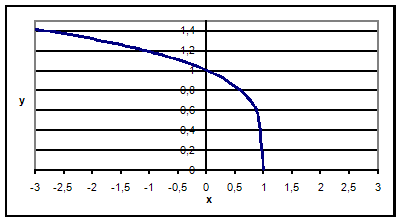
4. Точки пересечения функции с осями координат: (0, 1), (1,0).
5. Экстремум функции 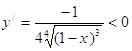 , следовательно, функция y(x) убывает
, следовательно, функция y(x) убывает
6. Выпуклость, вогнутость функции:
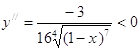 , следовательно, кривая выпукла
, следовательно, кривая выпукла
Значения функции ![]()
| x | y | x | y |
| -3 | 1,414214 | -1 | 1,189207 |
| -2,9 | 1,405291 | -0,9 | 1,174055 |
| -2,8 | 1,396194 | -0,8 | 1,158292 |
| -2,7 | 1,386917 | -0,7 | 1,141858 |
| -2,6 | 1,377449 | -0,6 | 1,124683 |
| -2,5 | 1,367782 | -0,5 | 1,106682 |
| -2,4 | 1,357906 | -0,4 | 1,087757 |
| -2,3 | 1,347809 | -0,3 | 1,06779 |
| -2,2 | 1,337481 | -0,2 | 1,046635 |
| -2,1 | 1,326907 | -0,1 | 1,024114 |
| -2 | 1,316074 | 0 | 1 |
| -1,9 | 1,304967 | 0,1 | 0,974004 |
| -1,8 | 1,293569 | 0,2 | 0,945742 |
| -1,7 | 1,281861 | 0,3 | 0,914691 |
| -1,6 | 1,269823 | 0,4 | 0,880112 |
| -1,5 | 1,257433 | 0,5 | 0,840896 |
| -1,4 | 1,244666 | 0,6 | 0,795271 |
| -1,3 | 1,231493 | 0,7 | 0,740083 |
| -1,2 | 1,217883 | 0,8 | 0,66874 |
| -1,1 | 1,203801 | 0,9 | 0,562341 |
| -1 | 1,189207 | 1 | 0 |
График функции
Тригонометрические: функция ![]()
1. Область существования: ![]()
2. Четность: ![]() функция нечетная
функция нечетная
3. Функция непрерывна
4. Точки пересечения функции с осями координат: (0, 0), (![]() ,0),
,0), ![]()
5. Экстремум функции ![]()
![]()
![]()
![]()
![]() ,
, ![]()
Значения функции ![]()
| x | y | x | y | x | y | x | y |
| -31,4 | -30947,4 | -17,27 | 0 | 3,14 | -30,959 | 17,27 | -0,00346 |
| -30,615 | -9676,29 | -16,485 | 1623,773 | 3,925 | -21,5061 | 18,055 | 2023,979 |
| -29,83 | 0,091927 | -15,7 | 3869,525 | 4,71 | 0 | 18,84 | 6686,259 |
| -29,045 | 9048,639 | -14,915 | 1146,551 | 5,495 | 58,17235 | 19,625 | 2752,484 |
| -28,26 | 22562,26 | -14,13 | 0 | 6,28 | 247,6694 | 20,41 | 0,009432 |
| -27,475 | 7028,394 | -13,345 | -857,374 | 7,065 | 126,0212 | 21,195 | -3258,35 |
| -26,69 | 0 | -12,56 | -1981,26 | 7,85 | 0 | 21,98 | -10617 |
| -25,905 | -6390,02 | -11,775 | -566,904 | 8,635 | -224,652 | 22,765 | -4316,48 |
| -25,12 | -15847,2 | -10,99 | 0 | 9,42 | -835,868 | 23,55 | -0,02226 |
| -24,335 | -4907,58 | -10,205 | 381,5954 | 10,205 | -381,595 | 24,335 | 4907,579 |
| -23,55 | 0 | -9,42 | 835,8683 | 10,99 | -0,00023 | 25,12 | 15847,22 |
| -22,765 | 4316,479 | -8,635 | 224,6522 | 11,775 | 566,9042 | 25,905 | 6390,015 |
| -21,98 | 10617,01 | -7,85 | 0 | 12,56 | 1981,265 | 26,69 | 0,047166 |
| -21,195 | 3258,345 | -7,065 | -126,021 | 13,345 | 857,3739 | 27,475 | -7028,39 |
| -20,41 | 0 | 0 | 0 | 14,13 | 0,001039 | 28,26 | -22562,3 |
| -19,625 | -2752,48 | 0,785 | 0,171231 | 14,915 | -1146,55 | 29,045 | -9048,64 |
| -18,84 | -6686,26 | 1,57 | 0 | 15,7 | -3869,52 | 29,83 | -0,09193 |
| -18,055 | -2023,98 | 2,355 | -4,60118 | 16,485 | -1623,77 | 30,615 | 9676,285 |
| 31,4 | 30947,37 |
График функции ![]()
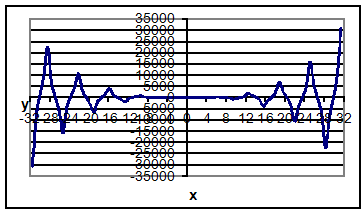
Гиперболические: функция ![]()
1. Область существования: ![]()
2. Четность: ![]() функция четная
функция четная
3. Функция непрерывна
4. Точки пересечения функции с осями координат: (0, 0)
5. Экстремум функции ![]()
![]()
![]()
![]()
![]()
Значения функции ![]()
| x | y | x | y | x | y |
| -3 | 1010,369 | -1 | 2,131145 | 1 | 2,131145 |
| -2,9 | 748,0854 | -0,9 | 1,510096 | 1,1 | 2,976561 |
| -2,8 | 553,8202 | -0,8 | 1,054878 | 1,2 | 4,125531 |
| -2,7 | 409,9402 | -0,7 | 0,722286 | 1,3 | 5,685108 |
| -2,6 | 303,383 | -0,6 | 0,480502 | 1,4 | 7,799941 |
| -2,5 | 224,4723 | -0,5 | 0,306196 | 1,5 | 10,66543 |
| -2,4 | 166,0397 | -0,4 | 0,182396 | 1,6 | 14,54546 |
| -2,3 | 122,7752 | -0,3 | 0,096937 | 1,7 | 19,79642 |
| -2,2 | 90,74509 | -0,2 | 0,04135 | 1,8 | 26,8995 |
| -2,1 | 67,03564 | -0,1 | 0,010084 | 1,9 | 36,50441 |
| -2 | 49,48836 | 0 | 0 | 2 | 49,48836 |
| -1,9 | 36,50441 | 0,1 | 0,010084 | 2,1 | 67,03564 |
| -1,8 | 26,8995 | 0,2 | 0,04135 | 2,2 | 90,74509 |
| -1,7 | 19,79642 | 0,3 | 0,096937 | 2,3 | 122,7752 |
| -1,6 | 14,54546 | 0,4 | 0,182396 | 2,4 | 166,0397 |
| -1,5 | 10,66543 | 0,5 | 0,306196 | 2,5 | 224,4723 |
| -1,4 | 7,799941 | 0,6 | 0,480502 | 2,6 | 303,383 |
| -1,3 | 5,685108 | 0,7 | 0,722286 | 2,7 | 409,9402 |
| -1,2 | 4,125531 | 0,8 | 1,054878 | 2,8 | 553,8202 |
| -1,1 | 2,976561 | 0,9 | 1,510096 | 2,9 | 748,0854 |
| -1 | 2,131145 | 1 | 2,131145 | 3 | 1010,369 |
График функции
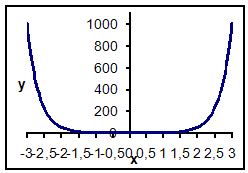
Натуральные логарифмы: функция ![]()
1. Область существования: ![]()
2. Четность: ![]() функция ни четная, ни нечетная
функция ни четная, ни нечетная
3. Функция непрерывна. 4. Точки пересечения функции с осями координат: (0, 0)
5. Экстремум функции 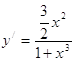
![]()
![]()
![]()
![]()
6. Точки перегиба: ![]()
![]()
![]()
![]()
![]() ,
, ![]()
Значения функции ![]()
| x | y | x | y |
| -1 | 1 | 0,346574 | |
| -0,9 | -0,65282 | 1,1 | 0,423149 |
| -0,8 | -0,35872 | 1,2 | 0,501784 |
| -0,7 | -0,21004 | 1,3 | 0,581106 |
| -0,6 | -0,12167 | 1,4 | 0,660077 |
| -0,5 | -0,06677 | 1,5 | 0,737953 |
| -0,4 | -0,03307 | 1,6 | 0,814228 |
| -0,3 | -0,01369 | 1,7 | 0,888577 |
| -0,2 | -0,00402 | 1,8 | 0,960809 |
| -0,1 | -0,0005 | 1,9 | 1,03083 |
| 0 | 0 | 2 | 1,098612 |
| 0,1 | 0,0005 | 2,1 | 1,164175 |
| 0,2 | 0,003984 | 2,2 | 1,227567 |
| 0,3 | 0,013321 | 2,3 | 1,288857 |
| 0,4 | 0,031018 | 2,4 | 1,348124 |
| 0,5 | 0,058892 | 2,5 | 1,405454 |
| 0,6 | 0,097783 | 2,6 | 1,460935 |
| 0,7 | 0,147453 | 2,7 | 1,514656 |
| 0,8 | 0,206717 | 2,8 | 1,566703 |
| 0,9 | 0,273772 | 2,9 | 1,617158 |
| 1 | 0,346574 | 3 | 1,666102 |
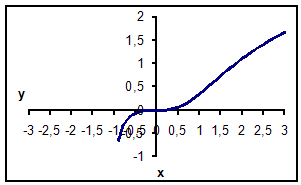
Сочетание тригонометрических, гиперболических: функция ![]()
1. Область существования: ![]() . Точка разрыва
. Точка разрыва ![]() .
.
2. Четность: ![]() функция четная.
функция четная.
4. Точек пересечения функции с осями координат нет.
5. Экстремум функции 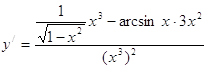
Значения функции ![]()
| x | y |
| -1 | 1,570796 |
| -0,9 | 1,536035 |
| -0,8 | 1,811123 |
| -0,7 | 2,260634 |
| -0,6 | 2,979172 |
| -0,5 | 4,18879 |
| -0,4 | 6,429951 |
| -0,3 | 11,28491 |
| -0,2 | 25,16974 |
| -0,1 | 100,1674 |
| 0 | |
| 0,1 | 100,1674 |
| 0,2 | 25,16974 |
| 0,3 | 11,28491 |
| 0,4 | 6,429951 |
| 0,5 | 4,18879 |
| 0,6 | 2,979172 |
| 0,7 | 2,260634 |
| 0,8 | 1,811123 |
| 0,9 | 1,536035 |
| 1 | 1,570796 |
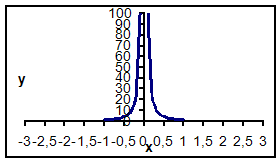
Задание 2. Выполнить исследование методами математического анализа уравнения функции и определить значения аргумента и параметра (если он имеется). Вид уравнения выбирается самостоятельно
Циссоида![]()
![]() (
(![]()
Обе функции ![]() и
и ![]() определены при всех
значениях
определены при всех
значениях ![]() . Заметим, что
. Заметим, что ![]() ,
, ![]() при
при ![]() . Найдем производные
. Найдем производные ![]() и
и ![]() :
:
![]()
![]()
![]() при
при ![]() ,
, ![]() при
при ![]() .
.
Для параметра t
получили критическую точку ![]() .
.
Далее, находим
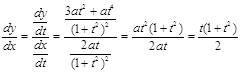
Составляем таблицу:
Область изменения t |
Соответствующая область изменения x | Соответствующая область изменения y |
Знак dy/dx |
Характер изменения yкак функции от x |
|
|
|
|
– | убывает |
|
|
|
|
+ | возрастает |
Найдем 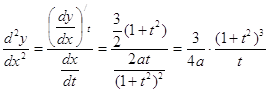
![]() при
при ![]() -
кривая вогнута;
-
кривая вогнута; ![]() при
при ![]() -
кривая выпукла
-
кривая выпукла
Точка 0 – точка возврата (такая точка, где направление движения вдоль кривой скачкообразно меняется на противоположное).
Вертикальная асимптота: ![]() .
.
Значения функции ![]()
![]() (при
(при ![]()
| t | x | y |
| -3 | 0,9 | -2,7 |
| -2,9 | 0,89373 | -2,59182 |
| -2,8 | 0,886878 | -2,48326 |
| -2,7 | 0,879373 | -2,37431 |
| -2,6 | 0,871134 | -2,26495 |
| -2,5 | 0,862069 | -2,15517 |
| -2,4 | 0,852071 | -2,04497 |
| -2,3 | 0,841017 | -1,93434 |
| -2,2 | 0,828767 | -1,82329 |
| -2,1 | 0,815157 | -1,71183 |
| -2 | 0,8 | -1,6 |
| -1,9 | 0,78308 | -1,48785 |
| -1,8 | 0,764151 | -1,37547 |
| -1,7 | 0,742931 | -1,26298 |
| -1,6 | 0,719101 | -1,15056 |
| -1,5 | 0,692308 | -1,03846 |
| -1,4 | 0,662162 | -0,92703 |
| -1,3 | 0,628253 | -0,81673 |
| -1,2 | 0,590164 | -0,7082 |
| -1,1 | 0,547511 | -0,60226 |
| -1 | 0,5 | -0,5 |
| -0,9 | 0,447514 | -0,40276 |
| -0,8 | 0,390244 | -0,3122 |
| -0,7 | 0,328859 | -0,2302 |
| -0,6 | 0,264706 | -0,15882 |
| -0,5 | 0,2 | -0,1 |
| -0,4 | 0,137931 | -0,05517 |
| -0,3 | 0,082569 | -0,02477 |
| -0,2 | 0,038462 | -0,00769 |
| -0,1 | 0,009901 | -0,00099 |
| 0 | 0 | 0 |
| 0,1 | 0,009901 | 0,00099 |
| 0,2 | 0,038462 | 0,007692 |
| 0,3 | 0,082569 | 0,024771 |
| 0,4 | 0,137931 | 0,055172 |
| 0,5 | 0,2 | 0,1 |
| 0,6 | 0,264706 | 0,158824 |
| 0,7 | 0,328859 | 0,230201 |
| 0,8 | 0,390244 | 0,312195 |
| 0,9 | 0,447514 | 0,402762 |
| 1 | 0,5 | 0,5 |
| 1,1 | 0,547511 | 0,602262 |
| 1,2 | 0,590164 | 0,708197 |
| 1,3 | 0,628253 | 0,816729 |
| 1,4 | 0,662162 | 0,927027 |
| 1,5 | 0,692308 | 1,038462 |
| 1,6 | 0,719101 | 1,150562 |
| 1,7 | 0,742931 | 1,262982 |
| 1,8 | 0,764151 | 1,375472 |
| 1,9 | 0,78308 | 1,487852 |
| 2 | 0,8 | 1,6 |
| 2,1 | 0,815157 | 1,71183 |
| 2,2 | 0,828767 | 1,823288 |
| 2,3 | 0,841017 | 1,93434 |
| 2,4 | 0,852071 | 2,04497 |
| 2,5 | 0,862069 | 2,155172 |
| 2,6 | 0,871134 | 2,264948 |
| 2,7 | 0,879373 | 2,374306 |
| 2,8 | 0,886878 | 2,483258 |
| 2,9 | 0,89373 | 2,591817 |
| 3 | 0,9 | 2,7 |
График функции
Список использованной литературы
1. Гай Харт-Девис WORD 2000. Базовый курс: Пер. с англ. – К.:ВЕК+,М:ЭНТРОП, СПБ: Корона-Принт, 2000. – 400 с., ил.
2. Джен Вейсскопф EXCEL 2000. Базовый курс (русифицированная версия): пер. с англ. – К.:ВЕК+, М.:ЭНТРОП, СПБ.: Корона-Принт, 2000. – 400 с., ил.
3. Пискунов Н.С. Дифференциальное и интегральное исчисления , том 1: учебное пособие для втузов. – 13-е изд. – М.: Наука, 1985. – 432 с.
4. Выгодский М.Я. Справочник по высшей математике. – М.:Физматгиз, 1963– 872с.