Курсовая работа: Види розподілу ймовірностей й оцінка його параметрів

Зміст

Вступ

1. Види розподілу ймовірностей

1.1 Біноміальний розподіл

1.2 Розподіл Х²

1.3 Розподіл Стьюдента

1.4 Розподіл F Фишера-Снедекора

2. Емпірична функція розподілу

3. Точечні та інтервальні оцінки параметрів розподілу

3.1 Точечна оцінка параметрів розподілу

3.2 Поняття інтервальної оцінки. Інтервальні оцінки параметрів нормального розподілу

4. Розподіл Пуассона

Висновок

Список літератури

Вступ

Предмет теорії ймовірностей. Події, що спостерігаються нами, (явища) можна підрозділити на наступні три види: достовірні, неможливі і випадкові.

Достовірним називають подія, що обов'язково відбудеться, якщо буде здійснена визначена сукупність умов S.

Наприклад, якщо в судині міститься вода при нормальному атмосферному тиску і температурі 20º, то подія "вода в судині знаходиться в рідкому стані" є достовірне. У цьому прикладі задані атмосферний тиск і температура води складають сукупність умов S.

Неможливим називають подія, що свідомо не відбудеться, якщо буде здійснена сукупність умов S.

Наприклад, подія "вода в судині знаходиться у твердому стані свідомо не відбудеться, якщо буде здійснена сукупність умов попереднього приклада.

Випадковим називають подію, що при здійсненні сукупності умов S може або відбутися, або не відбутися.

Наприклад, якщо кинута монета, то вона може упасти так, що зверху буде або герб, або напис. Тому подія "при киданні монети випав герб" - випадкове.

Кожна випадкова подія, зокрема - випадання герба, є наслідок дії дуже багатьох випадкових причин (у нашому прикладі: сила, з яким кинута монета, форма монети і багато хто інші). Неможливо врахувати вплив на результат усіх цих причин, оскільки число їхній дуже велике і закони їхньої дії невідомі. Тому теорія ймовірностей не ставить перед собою задачу пророчити, відбудеться одинична подія чи ні, - вона просто не в силах це зробити.

По-іншому обстоїть справа, якщо розглядаються випадкові події, щ о можуть багаторазово спостерігатися при здійсненні тих самих умов S, тобто якщо мова йде про масові однорідні випадкові події. Виявляється, що досить велике число однорідних випадкових подій, незалежно від їхньої конкретної природи, підкоряється визначеним закономірностям, а саме - вероятнісним закономірностям. Установленням цих закономірностей і займається теорія ймовірностей

Коротка історична довідка. Перші роботи, у яких зароджувалися основні поняття теорії ймовірностей, являли собою спроби створення теорії азартних ігор (Кардано, Гюйгенс, Паскаль, Ферма й ін. у XVI–XVII ст.).

Наступний етап розвитку теорії ймовірностей зв'язаний з ім'ям Якова Бернуллі (1654–1705). Доведена ним теорема, що одержала згод ом назву "Закону великих чисел", була першим теоретичним обґрунтуванням накопичених раніше фактів.

Подальшими успіхами теорія ймовірностей зобов'язана Муавру, Лапласові, Гауссу, Пуассонові та ін.

Новий, найбільш плідний, період зв'язаний з іменами П.Л. Чебишева (1821–1894) і його учнів А.А. Маркова (1856–1922) і А.М. Ляпунова (1857–1918). У цей період теорія ймовірностей стає стрункою математичною наукою, її наступний розвиток зобов'язаний, у першу чергу, російським і радянським математикам (С.Н. Бернштейн, В.І. Романовский, А.Н. Колмогоров, А.Я. Хінчин, Б.В. Гнеденко, Н.В. Смирнов і ін.). В даний час ведуча роль у створенні нових галузей теорії ймовірностей також належить радянським математикам.



1. Види розподілу ймовірностей

1.1 Біномінальний розподіл

Нехай виробляється п незалежних іспитів, у кожнім з який подія А може з'явитися, або не з'явитися. Імовірність настання події у всіх іспитах постійна і дорівнює р (отже, імовірність непояви q=l-p). Розглянемо в якості дискретної випадкової величини X число появ події А в цих іспитах.

Поставимо перед собою задачу: знайти закон розподілу величини X. Для її рішення потрібно визначити можливі значення X і їхньої імовірності.

Очевидно, подія А у п іспитах може або не з'явитися, або з'явитися 1 раз, або 2 рази,..., або п раз. Таким чином, можливі значення X такі:

Залишається знайти імовірності цих можливих значенні, для чого досить скористатися формулою Бернуллі:

(1.1)

де  =0, 1, 2,..., п.

Формула (1.1) і є аналітичним вираженням шуканого закону розподілу. Біномінальним називають розподіл ймовірностей, обумовлений формулою Бернуллі.

Закон названий "біномінальним" тому, що праву частину рівності (1.1) можна розглядати як загальний член розкладання бінома Ньютона

 (1.2)

Таким чином, перший член розкладання  визначає імовірність настання розглянутої події п раз у п незалежних, іспитах; другий член  визначає імовірність настання події п-1 раз;...; останній член  визначає імовірність того, що подія не з'явиться жодного разу. Напишемо біномінальний закон у виді таблиці:

Приклад:

Монета кинута 2 рази. Написати у виді таблиці закон розподілу випадкової величини X - числа випадань герба.

Рішення:

Імовірність появи герба в кожнім киданні монети  отже, імовірність не появи герба:

При двох киданнях монети герб може з'явитися або 2 рази, або 1 раз, або зо всім не з'явитися. Таким чином, можливі значення X такі:

Знайдемо імовірності цих можливих значенні по формулі Бернуллі:

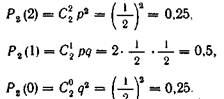
Напишемо шуканий закон розподілу:

Контроль:

1.2 Розподіл Х²

Нехай (і=1,2,...,п)- нормальні незалежні випадкові величини, причому математичне чекання кожної з них дорівнює нулю, а середнє квадратичне відхилення - одиниці. Тоді сума квадратів цих величин

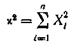
розподілена за законом Х² ("хи квадрат") з k=n ступенями волі; якщо ж ці величини зв'язані одним лінійним співвідношенням, наприклад , те число ступенів волі k=n-l. Диференціальна функція цього розподілу

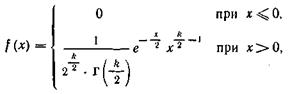
Де - гамма-функція; зокрема

Звідси видно, що розподіл "хи квадрат" визначається одним параметром - числом ступенів волі k. Зі збільшенням числа ступенів волі розподіл повільний наближається до нормального.

1.3 Розподіл Стьюдента

Нехай Z - нормальна випадкова величина, причому M(Z)=0, cy(Z) - 1, а V - незалежна від Z величина, що розподілена за законом /2 з k ступенями волі.

Тоді величина

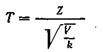
має розподіл, що називають t-розподілом, чи розподілом Стьюдента (псевдонім англійського статистика В. Госсета) з k ступенями волі.

Отже, відношення нормованої нормальної величини до квадратного кореня з незалежної випадкової величини, розподіленої за законом "хи квадрат" з k ступенями волі, діленої на k, розподілено за законом Стьюдента з k ступенями волі.

Зі зростанням числа ступенів волі розподіл Стьюдента швидко наближається до нормального. Додаткові зведення про цей розподіл приведені далі

1.4 Розподіл F Фішера-Снедекора

Якщо U і V незалежні випадкові величини, розподілені за законом х2 зі ступенями волі  і , те величина

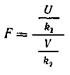
має розподіл, що називають розподілом F Фішера-Снедекора зі ступенями волі  і  (іноді його позначають через V²). Диференціальна функція

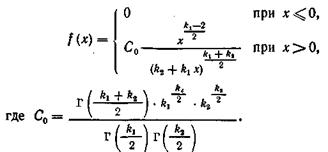
Ми бачимо, що розподіл F визначається двома параметрами - числами ступенів волі.

2. Емпірична функція розподілу

Нехай відомо статистичний розподіл частот кількісної ознаки X. Введемо значення п _х — число спостережень, менше х; п — загальне число спостережень (об’єм вибірки). Ясно, що відносна частота події X <1 дорівнює n(x)/п. Якщо х змінюється, то, взагалі говорячи, змінюється і відносна частота, тобто відносна частота п_х /п є функція від х. Тому що ця функція знаходиться емпіричним (досвідченим) шляхом, то її називають емпіричною.

Емпіричною функцією розподілу (функцією розподілу вибірки) називають функцію F*(x), що визначає для кожного значення х відносну частоту випадку X < х. '

Отже, по визначенню:

F(x)=nx/n

Де nx-число варіант, менших х; п — об'єм вибірки. Таким чином, для того щоб знайти, наприклад, F*(xi), потрібно число варіант, менших х_г, розділити на об’єм вибірки: F*(x2) = nx2/n.

На відміну від емпіричної функції розподілу вибірки функцію розподілу F (х) генеральної сукупності називають теоретичною функцією розподілу. Різниця між емпіричної і теоретичної функціями полягає в тому, що теоретична функція F (х) визначає імовірність події X < х, а емпірична функція F* (х) визначає відносну частоту події. З теореми Бернуллі випливає, що відносна частота події X < х, тобто F* (х) прагне по імовірності до імовірності F (х) цієї події. Іншими словами, при великих п числа F* (х) і F (х) мало відрізняються одне від іншого в тому змісті, що lim n-¥Р [ | F (х)- F* (х) | < е] = 1 (е > 0). Уже звідси випливає доцільність використання емпіричної функції розподілу вибірки для наближеного представлення теоретичної (інтегральної) функції розподілу генеральної сукупності.

Такий висновок підтверджується і тим, що F*(x) наділене усіма властивостями F (х). Дійсно, з визначення функції F* (х) випливають наступні її властивості: 1) значення емпіричної функції належать відрізку [О, 1];

2) F*(x) — функція, що не спадає;

3) якщо Xi — найменша варіанта, то F*(x) = Q при xx₁; якщо x_k—найбільша варіанта, то F* (х) = 1 при x> x_k.

Отже, емпірична функція розподілу вибірки служить для оцінки теоретичної функції розподілу генеральної сукупності.

Приклад.

Побудувати емпіричну функцію по даному розподілу вибірки:

варіанти x_i 2 6 10

частоти n_i 12 18 30

Розв’язок. Знайдемо обсяг вибірки: 12 + 18 + 30 = 60. Найменша варіанта дорівнює 2, отже,

F*(x) = О при x2. І

Значення X < 6, а саме x₁ = 2, спостерігалося 12 разів, отже,

:F*(x) = 12/60 = 0,2 при

2<x6. I

значення x<10, а саме x₁ = 2 і х₂ = 6, спостерігалися 12 + 18 = 30 разів, отже,

F* (х) = 30/60 = 0,5 при 6 < х  10. Тому що x=10 — найбільша варіанта, то | F*(x)=1 при х > 10. Шукана емпірична функція

Графік цієї функції зображений на малюнку.

3. Точечні та інтервальні оцінки параметрів розподілу

3.1 Точечна оцінка параметрів розподілу

Є два підходи до оцінювання невідомих параметрів розподілів по спостереженнях: точечний і інтервальний. Точечний вказує лише точку, біля якої знаходиться оцінюваний параметр; при інтервальному знаходять інтервал, що з деякою великою ймовірністю, що задається дослідником, накриває невідоме числове значення параметра. У главі розглядаються методи точечного оцінювання параметрів; будуються інтервальні оцінки параметрів нормального розподілу, обговорюється загальний підхід до інтервального оцінювання параметрів розподілу, відмінних від нормального.

3.1.1 Метод моментів

Метод моментів є одним із методів точечного оцінювання параметрів розподілу.

Нехай закон розподілу випадкової величини X відомий із точністю до числових значень його параметрів ₁,_2,…,k. Це означає, що відомий вид функції щільності f_x(х, ), де = (₁,_2,…,k), якщо X безперервна (відомий вид функції ймовірності Р (X= х,), якщо X дискретна), але числові значення k параметрів не відомі. Знайдемо оцінку = (₁,_2,…,k) параметра 0, розташовуючи вибіркою: х₁, х₂..., х_п.

Допустимо, що існує k початкових моментів, кожний із який можна висловити через  (без обмеження спільності можна розглядати тільки початкові моменти, тому що центральні моменти є функціями початкових). Нехай такими моментами будуть перший, другий,..., k-й: v₁,v_2,…,v_k (що зовсім не обов'язково). Висловимо кожний із них через :

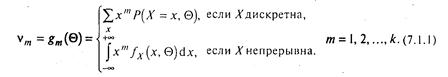                (3.1)

Помітимо, що в системі

                                    (3.2)

число рівнянь повинно бути рівним числу k оцінюваних параметрів. Знайдемо рішення системи (3.2). Висловивши кожний параметр q через v₁,v_2,…,v_k, одержимо:

                                    (3.3)

Властивість змістовності вибіркових початкових моментів є підставою для заміни в рівняннях (3.3) теоретичних моментів v₁,v_2,…,v_k на обчислені при великому п вибіркові моменти v₁,v_2,…,v_k.

Оцінками методу моментів параметрів ₁,_2,…,k називаються оцінки

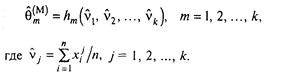                     (3.4)

Питання про те, які початкові моменти включати в систему (3.2), варто вирішувати, керуючись конкретними цілями дослідження і порівняльної простоти форм залежностей моментів від параметрів. У статистичній практиці справа рідко доходить навіть до четвертих моментів.

Приклад 3.1.1 Випадковий розмір Х~ N (а, σ), при цьому числові значення параметрів а і σ² не відомі. Знайдемо оцінки методу моментів для цих параметрів.

Використовуючи формулу (3.1), висловимо моменти v₁ і v₂ через а й σ²:

(v₁=a)∩(v₂=а² + σ²)- такий вид системи (3.2) у даному прикладі. Вирішивши її щодо а й σ ², одержимо: а = v₁ σ² = v₂ - v₁². Звідси оцінки методу моментів:

це оцінка математичного чекання а;

це оцінка дисперсії σ².

Відзначена раніше деяка невизначеність вибору початкових моментів може привести до одержання різних оцінок того самого параметра.

Приклад 3.1.2 Випадковий розмір X має розподіл Пуассона:

Знайдемо оцінку параметра X для двох

варіантів:

а) у якості початкового моменту візьмемо v1, одержимо:

б) у якості початкового моменту візьмемо v2; одержимо:

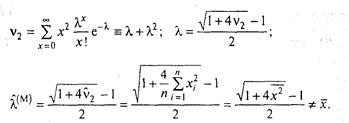
Оцінки - різні. Звичайно, краще перша: А, = х як більш проста і відповідному змісту параметра пуассонівського розподілу:

l = MX, тому за А, природно прийняти х - гарну точечну оцінку математичного чекання.

Однак не всі одержувані методом моментів оцінки мають властивості «гарної оцінки». Так, отримана в прикладі 3.1.1 оцінка

дисперсії σ² не має властивість незміщеності а є асимптотично незміщеною оцінкою: lim мd= limn-1/n*=, тобто при великих п можна вважати, що не зміщена щодо .

Приведемо без доказу теорему про функції від моментів, із якої випливають визначені властивості оцінок методу моментів.

Припустимо, що  є функцією двох вибіркових моментів vk і vm: =h(v,vm), що не містить явно п. Позначимо  =h(v,vm), де vk =Mvk, a vm = M/vm (останні дві рівності вірні в силу властивості незміщенності вибіркових початкових моментів),

Теорема стверджує: якщо в деякій околиці точки (v,vm), функція h безперервна зі своїми першими і другими похідними, то при великих п розподіл випадкового розміру =h(v,vm) близько до нормального (n має асимптотично нормальний розподіл) із математичним чеканням, рівним В, і дисперсією, рівної

                       (3.5)

де С²() — деяка постійна, що залежить від . (Теорему можна поширити на будь-яку кількість моментів — аргументів функції h)

З теореми випливає, що при виконанні досить загальних умов оцінка методу моментів ), при великих п задовольняє наступним співвідношенням:

                                       (3.6)

тобто оцінка методу моментів є асимптотично незміщенною,

                                             (3.7)

Переконаємося в тому, що  має властивість забезпеченості. Дійсно, нерівність Чебішева для розміру  при великих п, прийме вид:

звідси одержимо, що при п - P(/-/<)1.

Уведемо поняття ефективності й асимптотичної ефективності незміщеної оцінки скалярного параметра .

Ефективністю е() незміщеної оцінки  параметра  називають відношення min DQn(є s) — мінімально можливого значення дисперсії оцінки в класі S всіх незміщених оцінок параметра  до дисперсії Dn розглянутої оцінки. При виконанні функцією щільності f_х(х, 0) [функцією імовірності Р(Х =х, )] досить загальних умов регулярності: дифференційованих по , незалежності області визначення від  і т. д. — має місце нерівність Рао—Крамера—Фреше:

                                      (3.8)

де i() — кількість інформації про параметр , що міститься в одиничному спостереженні, визначається співвідношенням

                                   (3.9)

(i() — деяка постійна, що залежить від ). Тому

                    (3.10)

якщо е() = 1, то  — ефективна оцінка параметра  у класі S усіх

його незміщенних оцінок.

Асимптотичної ефективністю оцінки  називають розмір

                                      (3.11)

якщо () = 1 то  — асимптотична  ефективна оцінка (очевидно, що ефективна оцінка буде й асимптотично ефективною). Знайдемо вираження для асимптотичної ефективності оцінки

. Тому що при великих п оцінку  можна вважати незміщеною, то з урахуванням формул (3.11,3.10,3.7) одержимо

Приклад 3.1.3 Переконаємося в тому, що знайдена методом моментів по випадковій вибірці з генеральної сукупності X ~ N (а, а) оцінка X параметра а є ефективної в класі не зміщених оцінок, а оцінка ² параметра ² є, після виключення зміщення, асимптотично ефективною.

Оцінка X - незміщена, і DX = ²/п. Припустивши, що ² відома, і використовуючи формулу (3.10), у якій, з обліком нормальності розподілу,

1(а) = М(dln f(x,a)/da) = 1/ ² одержимо, що е() = 1. Звідси X - ефективна оцінка.

Оцінка  - зміщена; виключивши зміщення, одержимо оцінку

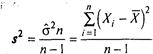
дисперсія котрої Ds =2/n-1.

Припустивши, що а відомо, і використовуючи вираження (3.10), у котрому, с обліком нормальності розподілу,

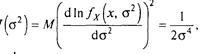
одержимо, що ефективність е(s2) =(n – 1/n)<1, а асимптотична эффективність e0(s2) = lim e(s2) = 1. Отже, s2 – асимптотична  эффективна оцінка.

Зауваження.

Незміщеною і ефективною оцінкою дисперсії є використовувана при відомому значенні параметра а оцінка s = (Xі -a) / п, тому що Мs = ², Ds = 2/n и е(s) = 1.

При виконанні досить загальних умов усі три оцінки: ²,s² і s забеспечені.

У приведеному прикладі оцінки методу моментів X і ² є відповідно ефективної й асимптотично ефективної. Однак подібні приклади швидке виключення: набагато частіше оцінки методу моментів із погляду ефективності не є найкращими з можливих навіть при великих п. Р. Фишер показав, що асимптотична ефективність цих оцінок часто значно менше одиниці. Асимптотично ефективні оцінки можуть бути отримані методом максимальної правдоподібності.

3.1.2 Метод максимальної правдоподібності

В основі методу максимальної правдоподібності лежить поняття функції правдоподібності. Нехай Х= (Х, Х₂,..., Х_п) — випадкова, а х = (х,х,..., х_п) — конкретна вибірки з генеральної сукупності X. Нагадаємо, випадкової називають вибірку, що задовольняє наступним умовам:

випадкові розміри Х, Х₂,,.., Х_п незалежні, тобто

                        (3.12)

            (3.13)

розподіл кожною з розмірів Х збігається з розподілом розміру X, тобто при і= 1, 2,..., n.

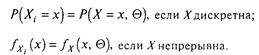                         (3.14)

Функція правдоподібності — це функція L (х, ), значення якої в точці х визначається співвідношенням:

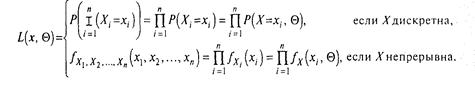
З визначення випливає: чим ймовірніше при фіксованому  набір х, тим більше значення функції правдоподібності L (x, ), звідси і її назва.

Отже,

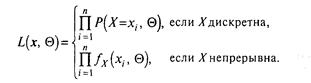               (3.15)

Відповідно до методу максимальної правдоподібності оцінка максимальної правдоподібності  ^(п) = (^п), ,..., ) параметра  = (, ,..., ), при заданому наборі х визначається з умови:

                                   (3.16)

де {} - область припустимих значень для .

Природність такого підходу до визначення оцінки  випливає зі змісту функції L: при фіксованому  функція L (х, 0) — міра правдоподібності набору х; тому, змінюючи , можна простежити, при яких його значеннях набір є більш правдоподібним, а при яких - менше, і вибрати таке значення , при якому наявний набір х буде найбільш правдоподібним.

У ряді випадків  зручніше визначати з умови:

In £(х, ) =  In L(x, )                               (3.17)

ідентичного умові (3.16): якщо замість функції L узяти In L, крапка максимуму не зміниться. Функцію In L (х, 0) називають логарифмічною функцією правдоподібності.

Відповідно до формули (3.17), для знаходження ^(П) випливає: знайти вирішення системи рівнянь максимальної правдоподібності

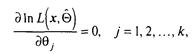                                      (3.18)

при цьому вирішенням вважається лише такий набір * = (*,*,..., *), що задовольняє (3.18), у якому кожне * дійсно залежить від х;

серед вирішень, що лежать усередині області {}, виділити крапки максимуму;

якщо система (3.18) не визначена, не розв'язна або якщо серед її вирішень немає крапки максимуму усередині {}, то крапку максимуму варто шукати на границі області {}.

Приклад 3.2.1 Знайдемо методом максимальної правдоподібності оцінки параметрів а і b = σ² нормального розподілу.

Відповідно до формули (3.15), функція правдоподібності

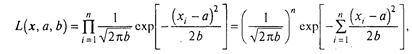
логарифмічна функція правдоподібності

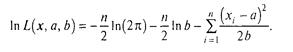
Приватні похідні:

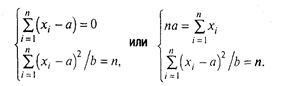
Перевіримо достатні умови максимуму функції In L у точці (а*, b*).

Знайдемо:

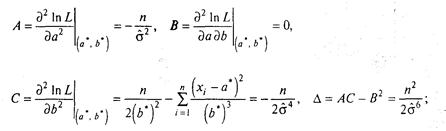
тому що ∆ >0, А<0, то крапка (а* = ,b*= ] є крапкою максимуму функції In L. Тому оцінки максимальної правдоподібності =х, =. Оцінки збіглися з оцінками методу моментів.

Приклад 3.2.2 Знайдемо методом максимальної правдоподібності оцінки параметрів а і b рівномірного на відрізку [а,b] розподіли. Відповідно до формули (3.15), функція правдоподібності

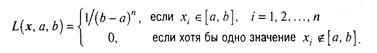
При першій умові система (3.18) не розв'язна, при другому - не визначена. Оцінки  і  варто шукати на границі області припустимих значень для а і b:

де а . Тоді умова (3.16) прийме вид:

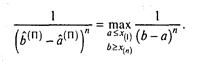
Тому що функція L(a,b) =1/(b - а)" убуває при зростанні b и убуванні а, то її максимум на області {} досягається в точці .

Приклад 3.2.4 Випадковий розмір Х- число успіхів в одиничному випробуванні: Р(Х = х) = р^х(1 – р) ^1-х, х = 0,1; р - імовірність успіху в одиничному випробуванні. Знайдемо оцінку максимальної правдоподібності  розташовуючи вибіркою х₁, х₂..., х_п, де х_і - число успіхів у і-м випробуванні.

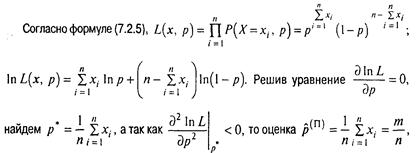
де т - число успіхів у л випробуваннях Бернуллі (таку ж оцінку можна одержати і методом моментів). Ця оцінка заможна, незміщена і, у чому неважко переконатися, ефективна.

Відзначена вище природність визначення оцінок максимальної правдоподібності з умови (3.16) підкріплюється їхніми гарними властивостями. Якщо функція щільності fx (х, 9) (функція імовірності Р(Х = х, 9), якщо-дискретна) задовольняє досить загальним умовам регулярності, оцінка максимальної правдоподібності  має при великих я розподіл, близький до нормального з математичним чеканням, рівним , і дисперсією, рівної 1/[пІ()], де І() визначається співвідношенням (3.9), є заможної, асимптично несумісної і асимптично ефективної; більш того, якщо існує ефективна оцінка параметра, вона буде єдиним вирішенням рівняння максимальної правдоподібності.

Крім описаних методів оцінювання параметрів існує ряд інших, наприклад метод найменших квадратів, відповідно до котрого

оцінка  параметра  знаходиться з умови:

                                       (3.19)

Звернемо увагу на те, що математичного чекання нормального розподілу з відомим значенням дисперсії умова (3.19) ідентично умові методу максимальної правдоподібності (3.16).

В останні роки розвиваються так називані робастні, або стійкі, методи оцінювання, що дозволяють знаходити оцінки, хоча і є не найкращими в рамках передбачуваного закону розподілу, але має досить стійкі властивості при відхиленні реального закону від передбачуваного.

3.2 Поняття інтервальної оцінки. Інтервальні оцінки параметрів нормального розподілу

Обчислена на основі вибірки оцінка  є лише наближенням до невідомого значення параметра  навіть у тому випадку, коли ця оцінка заможна, незміщена й ефективна. Виникає питання: не можна чи зазначити таке А, для якого з заздалегідь заданої близької до одиниці імовірністю 1 - α гарантувалося б виконання нерівності: |-| < ∆, або інакше, для котрого

                                 (3.2.1)

Якщо таке А існує, то інтервал (-∆, +∆) називають іньервальної оцінкою параметра 9, або довірчим інтервалом; -∆,  + ∆ — нижньої і верхньої довірчими границями; ∆ — помилкою оцінки , 1-α — надійністю інтервальної оцінки, або довірчою імовірністю. Вибір довірчої імовірності визначається конкретними умовами; звичайно використовуються значення 1 - α, рівні 0,90; 0,95; 0,99.

Оцінка , будучи функцією випадкової вибірки, є випадковим розміром, ∆ також випадкова: її значення залежить від імовірності 1 - α і, як правило, від вибірки. Тому довірчий інтервал випадковий і вираження (3.2.1) варто читати так: «Інтервал (-∆, +∆ накриє параметр  з імовірністю 1 — α», а не так: «Параметр  потрапить у інтервал (-∆, +∆ з імовірністю 1 - α».

У формулі (3.2.1) границі довірчого інтервалу симетричні щодо крапкової оцінки. Однак не завжди вдасться побудувати інтервал, що володіє такою властивістю. Для одержання довірчого інтервала найменшої довжини при заданому об'ємі виборки п і заданої довірчої імовірності 1 - а в якості оцінки  параметра  варто брати ефективну або асимптотично ефективну оцінку.

Існує два підходи до побудови довірчих інтервалів.

Перший підхід, якщо його вдасться реалізувати, дозволяє будувати довірчі інтервали при кожному кінцевому об'ємі вибірки п. Он заснований на доборі такої функції ψ (,), називаної надалі статистикою, щоб:

її закон розподілу був відомий і не залежав від ;

функція ψ(,) була безупинної і строго монотонної по .

Задавшись довірчою імовірністю 1- α, знаходять двосторонні критичні границі  , що відповідають імовірності а. Тоді з імовірністю 1 — α виконується нерівність І

                                          (3.2.2)

Вирішивши цю нерівність щодо 0, знаходять границі довірчого інтервалу для . Якщо щільність розподілу статистики в ψ(,) симетрична щодо осі 0у, то довірчий інтервал симетричний щодо .

Другий підхід, що одержав назву асимптотичного підходу, більш універсальний; однак він використовує асимптотичні властивості крапкових оцінок і тому придатний лише при досить великих об'ємах вибірки.

Розглянемо перший підхід на прикладах довірчого оцінювання параметрів нормального розподілу.

Інтервальна оцінка математичного чекання при відомій дисперсії. Отже, Х~ N (а, σ), причому значення параметра а не відомо, а значення дисперсії а² відомо.

При Х~ N (а, σ) ефективною оцінкою параметра а є X, при цьому X ~ N(a,σ а/√п). Статистика 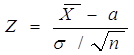 має розподіл N(0;1) незалежно від значення параметра а і як функція параметра а безупинна і строго монотонна. Отже, з обліком нерівності (3.2.2) і симетричності двосторонніх критичних границь розподілу y(0; 1) будемо мати:

Вирішуючи нерівність  щодо а, одержимо, що з імовірністю 1 - α виконується нерівність

                                     (3.2.3)

при цьому

                                                (3.2.4)

що відповідає результату (6.1.23); число и_а знаходять з умови Ф(u_а) = (1-α)/2.

Зауваження. Якщо п велике, оцінку (3.2.3) можна використовувати і при відсутності нормального розподілу розміру X, тому що в силу наслідку з центральної граничної теореми при випадковій вибірці великого об'єму п

Зокрема, якщо Х = ц, де ц - випадкове число успіхів у великому числі п випробувань Бернуллі, то

і з імовірністю ≈ 1 - α для імовірності р успіху в одиничному випробуванні виконується нерівність

                           (3.2.5)

Замінюючи значення p і q=1-pn лівій і правій частинах нерівності (3.2.4) їхніми оцінками  і , що припустимо при великому п, одержимо наближений довірчий інтервал для імовірності р:

                                     (3.2.6)

Приклад 3.2.1 Фірма комунального господарства бажає на основі вибірки оцінити середню квартплату за квартири визначеного типу з надійністю не менше 99% і погрішністю, меншої 10 д.е. Припускаючи, що квартплата має нормальний розподіл із середнім квадратичнім відхиленням, що не перевищує 35 д.е., знайдіть мінімальний об’єм вибірки.

Вирішення. За умовою потрібно знайти таке п, при якому , де а і Х- генеральна і вибіркова середні.

Прирівнявши 1 - α = 0,99, по табл. П. 4.1 знайдемо число и_а, при якому Ф() = (1 - α)/2 = 0,495; и_0.01= 2,6. При ∆ =10 і α = 35 із формули (3.2.4) одержимо п == 82,81. Але тому що з ростом 1 - α і зменшенням ∆ зростає п, то п > 82,81 і п_тin = 83 (звичайно, при зменшенні верхньої границі для про буде зменшуватися і п_тin). Т

Інтервальна оцінка математичного чекання при невідомій дисперсії. Отже, Х~ N (а, о), причому числові значення ні а, ні α ² не відомі. По випадковій вибірці знайдемо ефективну оцінку параметра а:  і оцінку  параметра σ².

Побудова інтервальної оцінки для а засновано на статистику , що при випадковій вибірці з генеральної сукупності Х~ N (а; σ) має розподіл Стьюдента з (п - 1) ступенем волі незалежно від значення параметра а і як функція параметра а безупинна і строго монотонна.

З обліком нерівності (3.2.2) і симетричності двосторонніх критичних границь розподілу Стьюдента будемо мати:

Вирішуючи нерівність -ta відносно а, одержимо, що з імовірністю 1 - α виконується нерівність

                                     (3.2.7)

і помилка оцінки X при невідомому значенні параметра о²

                                        (3.2.8)

де число знаходять по табл. П. 4.2 при k=n-1 пр = α.

Зауваження. При k=п-1>30 випадковий розмір t(k) має розподіл, близьке до N (0; 1), тому з імовірністю ≈ 1 - α

                      (3.2.9)

Приклад 3.2.2 Для галузі, що включає 1200 фірм, складені випадкова вибірка з 19 фірм. По вибірці опинилося, що у фірмі в середньому працюють 77,5 чоловік при середньому квадратичному відхиленні s = 25 чоловік. Користуючись 95%-нім довірчим інтервалом, оціните середнє число працюючих у фірмі по всій галузі і загальне число працюючих у галузі. Передбачається, що кількість працівників фірми має нормальний розподіл.

Вирішення. При k = n -1 = 18 і р = α = 1 - 0,95 = 0,05 знайдемо в табл. П. 4.2 t₀₀₅ = 2,10. Довірчий інтервал (3.2.7) прийме вид: (65,5; 89,5). З імовірністю 95% можна стверджувати, що цей інтервал накриє середнє число працюючих у фірмі по всій галузі. Тоді довірчий інтервал для числа працюючих у галузі в цілому такий: (1200-65,5; 1200-89,5). Т

Інтервальна оцінка дисперсії (середнього квадратичного відхилення) при відомому математичному чеканні. Ефективною оцінкою дисперсії в цьому випадку є .

Використовуються два варіанти інтервальної оцінки для σ²(σ).

1. Основу першого варіанта складає статистика

                                               (3.2.10)

який має розподіл%² із п ступенями волі незалежно від значення параметра а² і як функція параметра а² > О безупинна і строго монотонна.

Отже, з обліком нерівності (3.2.2) будемо мати:

де  і  — двосторонні критичні границі Х²-распределения з п ступенями волі.

Вирішуючи нерівність  щодо α², одержимо, що з імовірністю 1 — α виконується нерівність

                                             (3.2.11)

і з такою же імовірністю виконується нерівність

                                 (3.2.12)

Числа  і  знаходять по табл. П. 4.3 при k = п і відповідно при р=α/2 і р=1-α/2. Інтервальна оцінка (3.2.12) несиметрична щодо .

2. Другий варіант припускає знаходження інтервальної оцінки для а при заданій надійності 1 - α у виді

                                    (3.2.13)

При 5_а < 1 границі цієї оцінки симетричні щодо  і помилка оцінки , що гарантується з імовірністю 1 - α,

                                           (3.2.14)

Як знайти 8_а? Вирішуючи нерівність (3.2.13) щодо n/σ², одержимо, що з імовірністю 1 — α виконується нерівність

                             (3.2.15)

або, з огляду на формулу (3.2.10) і замінивши п на k, а α на р,

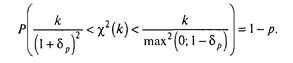                            (3.2.16)

Значення , задовольняють рівнянню (3.2.16) при різних р та k,приведені до таблиці П. 4.6.

Тоді,

                        (3.2.17)

де  — число, знайдене в табл. П. 4.6 при k = п и р = а.

Інтервальна оцінка дисперсії (середнього квадратичного відхилення) при невідомому математичному чеканні. Найкращою крапковою оцінкою дисперсії в цьому випадку є , і побудова інтервальної оцінки для а² засновано на статистику , який при випадковій вибірці з генеральної сукупності Х~ N(a; α) має розподіл Х² із (п — 1) ступенем волі.

Проробивши викладення для розміру Х²(п — 1), подібні викладенням при відомому математичному чеканні, одержимо два варіанти інтервальної оцінки для а² (σ):

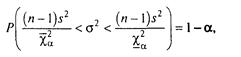                             (3.2.18)

                            (3.2.19)

де числа  і  знаходять по табл. П. 4.3 при k = п - 1 і відповідно при р = α/2 і р=- 1 - α/2.

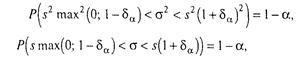(3.2.20)   (3.2.21)

при цьому помилка оцінки s, що гарантується з імовірністю 1 - α,

(3.2.22)

число 5_га знаходять по табл. П. 4.6 при k = п — 1 і р = α.

Зауваження. При k = п — 1 > 30 випадковий розмір Х²(к) має розподіл, близьке до , тому з імовірністю ≈ 1 - α

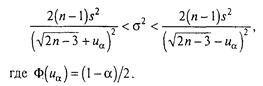                        (3.2.23)

Приклад 3.2.3 Варіація щодобового прибутку випадково обраних 10 кіосків деякої фірми, обмірюване розміром 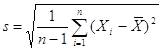 де  - прибуток і-го кіоска, опинилася рівної 100 д. е. Знайдіть таке ∆, при якому з надійністю 90% можна гарантувати, що варіація прибутку по всіх кіосках фірми не вийде за межі 100 + ∆. Передбачається, що прибуток - нормально розподілений розмір.

Тому що середній прибуток кіоску по усій фірмі не відомий і інтервал для про повинний бути симетричним щодо s, для розрахунку помилки оцінки s при 1 - а = 0,9 скористаємося формулою (3.2.22).

При k = 9 та р= α = 0,1 по табл. П. 4.6 знайдемо  = 0,476; тоді ∆ = 47,6. З надійністю 90% можна стверджувати, що генеральна варіація прибутку кіоску не вийде за межі 100 + 47,6.

Приклад 3.2.4 Користуючись 90%-нім довірчим інтервалом, оціните в умовах завдання 7.2 варіацію працюючих у фірмі по всій галузі.

Вирішення. За умовою п = 19, s = 25, 1 - α = 0,9. Знайдемо два варіанти довірчого інтервалу:

Відповідно формулі (3.2.19)

а тому що при k = п-1 = 18 верхня довірча границя , а нижня (див. табл. П. 4.3), то 19,740 < α < 34,613 - ця оцінка не симетрична щодо s.

2. Відповідно до рівняння (3.2.21),

а так як при k = п -1 = 18 50, = 0,297 (див. табл. П. 4.6), то 17,575<σ<32,425 - ця оцінка симетрична щодо s. Вона, як і випливало очікувати, відрізняється від попередньої інтервальної оцінки, однак

3.2.1 Асимптотичний підхід до інтервального оцінювання

З прикладами інтервальних оцінок, що мають місце тільки при великих об'ємах вибірок, ми вже зштовхувалися. Так, якщо розподіл випадкового розміру X відмінно від нормального, але п велике, то з імовірністю ≈ 1 - а інтервальна оцінка для MX = а має вид нерівності (3.2.3); з імовірністю ≈ 1-а інтервальна оцінка для р при великих п має вид нерівності (3.2.6) і т. д. [див. нерівності (3.2.9), (3.2.23)].

Розглянемо асимптотичний підхід у загальному випадку.

Раніше було встановлено, що при виконанні досить широких умов оцінка  параметра , отримана або методом моментів або методом максимальної правдоподібності, має в самому загальному випадку асимптотичний нормальний розподіл і асимптотично несумісної, тобто при великих п оцінка . Однак на відміну від ситуації, розглянутої на раніше, де дисперсія D оцінки передбачалася відомої, у загальному випадку дисперсія Dоцінки  залежить від оцінюваного невідомого параметра θ:

                                              (3.2.24)

Тому напряму перший підхід до довірчого інтервалу неприйнятий.

Порушимо питання так: не можна чи перетворити оцінку  у g – g() це невідомий параметр  у g = g (θ) так, щоб дисперсія D не залежала від θ. Викладемо схему добору такого перетворення, а потім пояснимо, як, використовуючи його, знайти інтервальну оцінку для θ.

Нехай θ — оцінка методу моментів: θ, а отже, і g = g(θ) є функціями вибіркових моментів. Тоді, відповідно до теореми про властивості функцій вибіркових моментів (див. 3.1), розподіл оцінки  при великих п близько до нормального,  і, з обліком виражень (3.5) і (3.2.25),

(аналогічні вираження утворюються і для оцінок максимальної правдоподібності в регулярному випадку). Але тому що дисперсія Dне повинна залежати від θ, то вираження c(θ) g'(θ) повинно бути постійним, наприклад, c(θ)g'(θ) = 1. Тоді g'(θ)= 1/ c(θ) і

                                              (3.2.25)

при цьому довільна постійна в невизначеному інтегралі вибирається з розумінь простоти остаточних виражень.

Отже, при великих п розподіл оцінки близько до нормального, при цьому , a  і, отже,

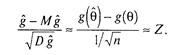
Тому при великих п для g(9) з імовірністю * I — а має місце нерівність, подібна нерівності (3.2.3):

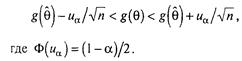                             (3.2.26)

Застосувавши до всіх частинам нерівності (3.2.26) перетворений не , що є зворотною функцією до функції g, одержимо інтервальну оцінку для θ.

Приклад 3.2.5 Побудуємо довірчий інтервал для параметра розподілення Пуассона: Р(Х = х) =л.

У прикладі 3.2.2 була знайдена оцінка методу моментів  параметра ;  будучи оцінкою методу моментів, має асимптотично нормальний розподіл (ця властивість оцінки  випливає також і з центральної граничної теореми), при цьому  - оцінка, тому що , а дисперсія оцінки , залежить від параметра λ:

Зіставивши вираження для  с вираженням (3.2.24), одержимо

і, відповідно до рівності (3.2.25),

З урахуванням виду функції нерівність (3.2.26)

                     (3.2.27)

Для функції  при х ≥ 0 і у ≥ 0 зворотна функція . Тому, якщо в нерівності (3.2.27)

то, застосувавши до всіх його частинам перетворення  одержимо нерівність

                           (3.2.28)

яке виконується при великих п з імовірністю ≈ 1 - α.

Приклад 3.2.6 Побудуємо довірчий інтервал для р - імовірності успіху в одиничному випробуванні.

У прикладі 3.2.4 методом максимальної правдоподібності для р була знайдена оцінка , де  - випадкове число успіхів у п випробуваннях Бернуллі; р має асимптотичний нормальний розподіл, при цьому М = р, a D= р(1 – р)/п - дисперсія залежить від параметра р.

Зіставивши вираження для D із вираженням (3.2.24), одержимо

і, відповідно до формули (3.2.25),

З обліком виду функції g(p) нерівність (3.2.26) прийме вид:

                   (3.2.29)

Для функції  при 0 <  < 1 зворотна функція , де 0 < у < π. Тому, якщо в нерівності (3.2.29)

 та , то застосувавши до всіх його частинам перетворення одержимо нерівність;

який виконується при великих п з імовірністю ≈ 1 - α.

4. Розподіл Пуассона

Нехай виробляється п незалежних іспитів, у кожнім з який імовірність появи події А дорівнює р. Для визначення імовірності k появ події в цих іспитах використовують формулу Бернуллі. Якщо ж п велико, то користаються асимптотичною формулою Лапласа. Однак, ця формула непридатна, якщо імовірність події мала (р≤0,1). У цих випадках (п велико, р мало) прибігають до асимптотичною формулою Пуассона.

Отже, поставимо своєю задачею знайти імовірність того, що при дуже великому числі іспитів, у кожнім з який імовірність події дуже мала, подія наступить рівно k раз.

Зробимо важливе допущення: добуток пр зберігає постійне значення, а саме і пр=λ. Як буде випливати з подальшого це означає, що середнє число появ події в різних серіях іспитів, тобто при різних значеннях п, залишається незмінним. Скористаємося формулою Бернуллі для обчислення цікавлячої нас імовірності:

Тому що пр=λ те  Отже,

Прийнявши в увагу, що п має дуже велике значення, замість  знайдемо . При цьому буде знайдене лише наближене значення імовірності, що відшукується: хоча і велико, але звичайно, а при відшуканні межі ми спрямуємо п д о нескінченності. Отже,

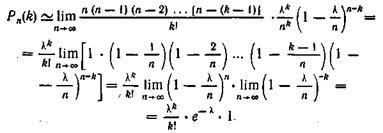
Отже (для простоти запису знак наближеної рівності опущений),

Ця формула виражає закон розподілу Пуассона імовірностей масових (п велике) рідких (р мале) подій.

Зауваження. Маються спеціальні таблиці користаючись якими можна з найти Pn(k). знаючи k і λ.

Висновок

У цій курсовій роботі ми розглянули апарат теорії ймовірностей і математичної статистики який використовується для аналізу динаміки об’ємів банківських депозитів. Цей апарат використовується у багатьох банківських системах та різних за призначенням галузях країн в тому числі і нашої країни.

Отже, предметом теорії ймовірностей є вивчення імовірнісних закономірностей масових однорідних випадкових подій. Знання закономірностей, яким підкоряються масові випадкові події, дозволяє передбачати, як ці події будуть протікати. Методи теорії ймовірностей широко застосовуються в різних галузях природознавства і техніки: у теорії надійності, теорії масового обслуговування, у теоретичній фізиці, геодезії, астрономії, теорії стрілянини, теорії помилок спостережень, теорії автоматичного керування, загальної теорії зв’язку й у багатьох інших теоретичних і прикладних науках. Теорія ймовірностей служить, також для обґрунтування математичної і прикладної статистики, що, у свою чергу, використовується при плануванні й організації виробництва, при аналізу технологічних процесів, попереджувальному і приємному контролі якості продукції та для багатьох інших цілей.

В останні роки методи теорії ймовірностей все ширше і ширше проникають в різні області науки і техніки, сприяючи їх прогресу.

Список літератури

1.    Колемаев В.А. Математическая экономика.- М: ЮНИТИ. 1998.

2.    Замков О.О., Толстопятенко А.В.. Черемніх Ю.Н. Математические методи в экономике.- М.: ДИС. 1997.

3.    Грубер И. Эконометрия.- Киев.: Изд. Астарта. 1996.

4.    Колемаев В.А. и др. Теория вероятностей и математическая статистика. - М.: Вісш. шк.. 1991.-400 с. 09. Толбатов Ю.А. Математична статистика та задачі оптимізації в алгоритмах і програмах. - Київ, 1991.

5.    Венцель Е.С.. Овчаров Л.Н. ТВ и ее инженерное приложение. - М.: Наука. 1988.

6.    Розанов Ю.А. Теория вероятностей, случайні процесси математическая статистика. - М.: Наука. 1985. 22. Айвазян С.А. и др. Прикладная статистика: Основи моделирования и первичная обработка даних. -М.: Финанси и статистика. 198?.-471 с.

7.    Айвазян С.А. и др. Прикладная статистика: Исследование зависимостей. — М.: Финансі и статистика. 1985. -487 с.

8.    Айвазян С.А. и др. Прикладная статистика: Классификация и снижение размерности. - М.: Финансі и статистика. 1989. - 607 с.

9.    Малахин В.И. Математическое моделирование экономики.-М.. 1998.

10. Красе М.С. Математика для экономических специальностей.- М.: ИНФРА-М. 1999.

11. Ляшенко И.Н.. Ляшенко Е.И. Математика для экономистов.- Донецк. 1998.

12. Сакович В.А. Исследование операций (детерминированніе методі и - модели) Справочное пособие.-Мн.: Віш.шк.. 1984.-254 с.

13. Зайченко Ю.П. Исследование операций.-К: Виша.шк.. 1988.

14. Вентцель Е.С. Исследование операций. Задачи, принципі, методология.-М.: Наука, 1980-208 с.