Контрольная работа: Высшая математика

Контрольная работа

высшая математика

ЗАДАЧА 1. Вычислить пределы функций а) —д):

а)        1..

  ►==.

  2. .

  ►.====0.

  3. ..

  ►.====-∞.

б)        .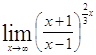

Решение.==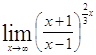

==

 ===

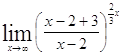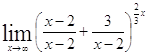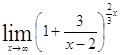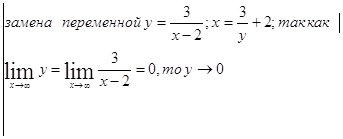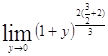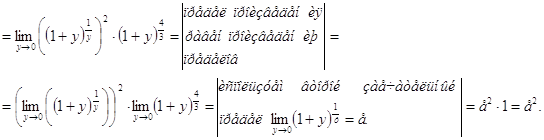
Предел  вычислен подстановкой

Предел  не может быть вычислен подстановкой , поскольку в результате подстановки получается неопределенность .

в) .

Анализ задачи. Подстановка числа 2 вместо  показывает, что пределы числителя и знаменателя равны нулю. Следовательно, нам потребуется раскрыть неопределенность . Для этого можно либо провести тождественные преобразования выражения , либо применить правило Лопиталя.

Решение. Выражение  является сопряженным по отношению к выражению , а выражение  - по отношению к . Умножая числитель и знаменатель дроби на произведение сопряженных выражений ()·(), и используя формулу разности квадратов , получаем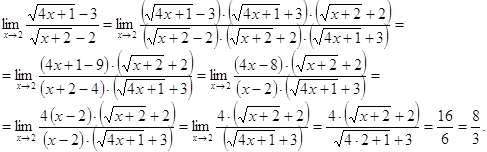

Другое решение задачи. Воспользуемся правилом Лопиталя

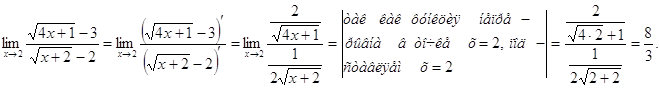
Анализ задачи. В данном случае, непосредственное применение те­оремы о пределе частного невозможного, поскольку, как показывает подстановка числа. -3 вместо x и предел числителя и предел знаме­натели равны пулю.

 и

Таким образом, рассматриваемый предел представляет собой неопределённость вида  и для решения задачи требуется про­вести тождественные преобразования выражения, находящего­ся под знаком предела.

Решение. Разложим числитель и знаменатель на множители, пользуясь следующей теоремой: если— корни квадратного трехчлена, то,

= Решаем квадратное уравнение, находя его дискриминант D.

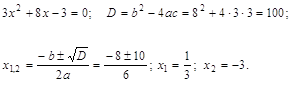
Отсюда,

Аналогично,

Поэтому,

  Преобразуем выражение находящиеся под знаком предела:

 ==

=

Другое решение задачи. Поскольку пределы числителя и знаменателя при

Равны нулю, применимо правило Лопиталя.

д)

Анализ задачи. Подстановка числа 0 вместо x показывает, что пределы числителя и знаменателя при  равны нулю. Поэтому, имеет место неопределённость .

Для того, чтобы раскрыть неопределённость можно либо провести тождественные преобразования выражения, либо применить правило Лопиталя.

  Решение. Совершим замену неизвестной при этом

Так как  при то

Используем теперь тригонометрическую формулу  

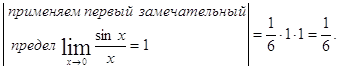
Другое решение. Воспользуемся вновь правилом Лопиталя

ЗАДАЧА 2. Вычислить производные функций а) – в):

а) Вычислить производную функции

►◄

б) Вычислить производную функции

1. .

►

◄

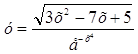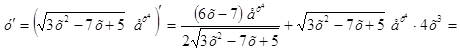
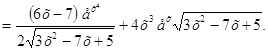в) Вычислить производную функции

.

►.◄

2. .

►

.◄

3.

►

.◄

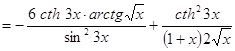ЗАДАЧА 3. Исследовать функцию и построить график

Исследовать функцию  и построить её график.

►Исследуем данную функцию.

1.           Областью определения функции является множество .

2.           Ордината точки графика .

3.           Точки пересечения графика данной функции с осями координат:

4.           Легко находим, что

.

Находим наклонные асимптоты:

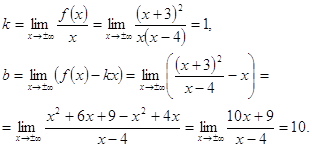
Таким образом, существует единственная наклонная асимптота

5. Исследуем функцию на возрастание, убывание, ло­кальный экстремум:'

y=  2(х + 3)(x-4)-(x + 3)²  _  2x² – 2x - 24 – х² - 6х - 9   =
(х-4)²                                     (x-4)²

=.

Из у' = 0 следует х^г — 8х — 33 = 0, откуда = 11, х₂₌— 3. В интервале (—∞; — 3) y'> 0, следовательно, функция возрастает в этом интервале; в (—3; 4) y'<0, т. е. функция убывает. Поэтому функция в точке х = —3 имеет локальный максимум: у( —3) = 0. В интервале (4; 11)

у' < 0, следовательно, функция убывает на этом интер­вале; в (11; +∞) у'>0, т. е. функции возрастает. В точке  = 11   имеем локальный  минимум:  y(ll) =28.

6.        Исследуем график функции на выпуклость, вогнутость   и  определим  точки   перегиба.  Для   этого  найдем

=

==.

Очевидно, что в интервале (—∞; 4) y"< 0, и в этом интервале кривая выпукла; в (4; +∞)

 у" > 0, т. е. в этом интервале кривая вогнута. Так как при х = 4 функция не определена, то точка перегиба отсутствует.

7.        График функции изображен на рис. 0.17

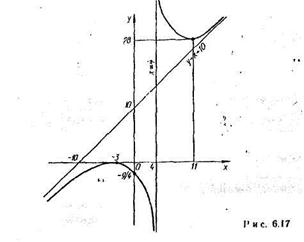
ЗАДАЧА 4. Вычислить неопределенные интегралы а) – в)

а)

1.

►◄

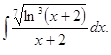
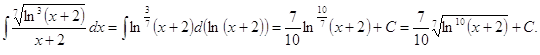2.

►

◄

3.

►

.◄

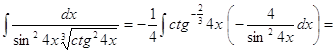
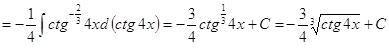4.

►

.◄

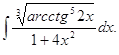
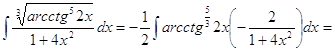
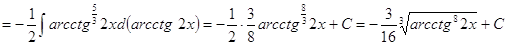б) .

Решение. Решение данной задачи на формуле интегрирования по частям:

В этой формуле принимаем за

 По формуле находим производственную второго сомножителя :

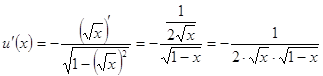
Подставляя найденные  в формулу интегрирования по частям получаем:

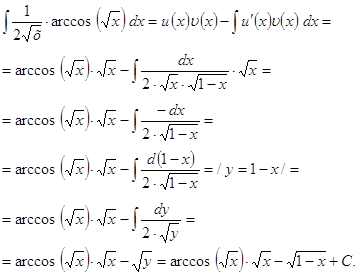
в) )

Решение. Так как корнями знаменателя является , то по формуле , знаменатель раскладываются на множители

.

Подставим дробь в виде следующей суммы:

,

и найдем коэффициенты А и В. Приведем дроби в правой равенства части к общему знаменателю:

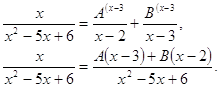
Приравняв числители, получим

         (2)                                   .

Подставив в последнее равенство , находим, что

Подставляя  в равенство (2), находим, что

Таким образом, .

Итак,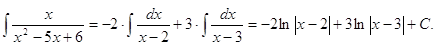

Здесь мы воспользуемся формулой (1)

ЗАДАЧА 5. Вычислите площадь фигуры, ограниченной графиками функций . Изобразите эту фигуру на координатной плоскости.

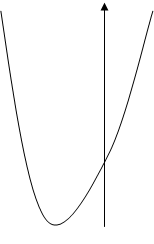
Решение. Графиком функции  является парабола, ветви которой направлены вверх. Вычисляем производную функции  и находим координаты вершины параболы С:

Рис. к задаче 5

Найдем точки пересечения графиков функции : .

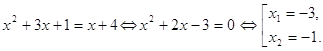
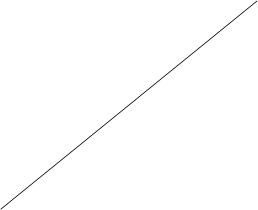
Заметим, что  Графиком функции является прямая, которую можно построить по двум точкам .

Пусть площадь фигуры , ограниченной графиками функций. Так как

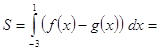
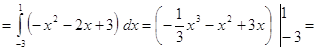
Дифференциальные уравнения с разделяющимися переменными. Дифференциальное уравнение вида

          (3)                                           

где  - заданные функции называются дифференциальным уравнением с разделяющимися переменными.

Для решения уравнения такого вида необходимо сделать следующее:

  1). Разделить переменные, т. е. Преобразовать уравнение к виду

           (4)                                 .

  2). Проинтегрировать обе части уравнения (4)

            (5)                                       

где  первообразная функции  первообразная функции  произвольная постоянная.

  3). Разрешить, если это возможно, уравнение (5) относительно y (и найти область определения решения):  

  4). Добавить к решению (5) все функции вида (горизонтальные прямые), где число

один из корней уравнения

Описанный метод решения можно схематично представить в виде формулы:

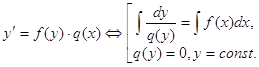
ЗАДАЧА 6. Найти общее решение дифференциального уравнения     Построить графики двух частных решений этого уравнения.

Решение. 1). Преобразуем уравнение к виду

Равенство  (у² + х²) = С показывает, что С > 0. Положим С =∙ R² ,где R > 0 — другая произвольная  постоянная. Тогда

у² + х² = R².

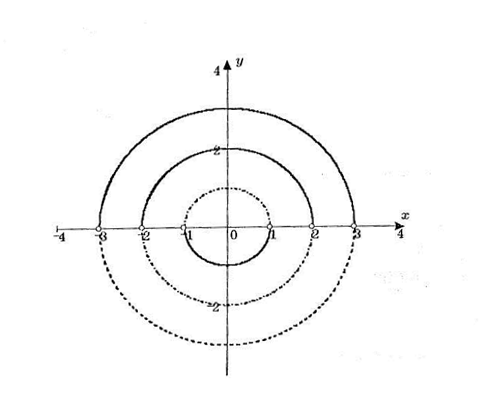
3). Разрешим, предыдущее уравнение относительно у и найдём область определения решения:

Рис. к задаче 6.

D(у) =>0. Графики решений — дуги концентрических окружностей произвольного радиуса с центром в на­чале координат (см. рис.).

4). В данном случае, уравнение не имеет решений. Поэтому решений вида

 y = а нет.   

Линейные дифференциальные уравнение второго порядка с постоянными коэффициентами. Уравнение  вида

(7)   у" + by' + су=0,

где b и с — некоторые числа, называется линейным однородным диф­ференциальным уравнением второго порядка с постоянными коэффи­циентами. Общее решение  этого уравнения в зависимости от знака дискриминанта

 характеристического уравнения

. (8)     k² + bk + c = 0

имеют следующий вид:

A) если D > 0, где k =α, к=β — два различных действительных корня (α≠β) характеристического уравнения (8);

Б)   , если D = О,

где α— единственный корень характеристического уравнения;

B)  если D < О,

где

Общее решение  линейного неоднородного дифференциаль­ного уравнения второго порядка с постоянными коэффициентами

(9)  

является суммой некоторого его частного решения  и общего решения

. однородного уравнения (7), т. е.

Многочлен  называют характеристическим мно­гочленом дифференциального уравнения (7).

В тех случаях, когда  представляет собой многочлен, функцию

 ,частное решение  удаётся найти подбором с помощью следующей таблицы.

1. :

2. если

3.

Задача 7. Найти частное решение дифференциального урав­нения  удовлетворяющее началь­ным условиям  у (0) = 1, у'(0) = 2.

Решение. 1). Характеристического  уравнение:

Так  как  D   =   — 16,   используем  формулу  В):   

   Общее решение однородного уравнения:

2). Так как правая часть многочлен второй степени, частное решение неоднородного уравнения бу­дем искать в виде многочлена 2-ой степени с неопределёнными коэффициентами:

Подставляя  у = в данное в задаче уравнение, получаем:

Сравнивая коэффициенты при одинаковых степенях х, нахо­дим:

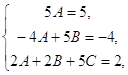
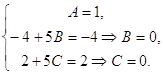
Отсюда  поэтому общее решение неоднородного уравнения имеет вид

3). Находим частное решение, удовлетворяющее начальным условиям, данным в задаче:

Напомним, что число n! (читается «эн-факториал»)- это произведение всех натуральных чисел от единицы до :

!=

При вычислениях с факториалами представляется важным следующее соображение:

и т.д.

Признак Даламбера. Если существует предел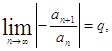

То числовой ряд сходится при  и расходится при

ЗАДАЧА 8. Исследовать сходимость ряда

Решение: .

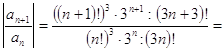
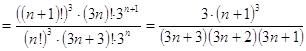
Вычисляем предел

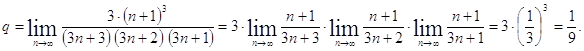
Таблицы и формулы.

1.      Производные основных элементарных функций

1). Производная константы равна нулю:

2). где  а — любое не равное нулю действительное число. В частности,

3). Показательная и логарифмическая функции.       

2.        Производные некоторых сложных функций:

1)        

2)                                                                    

3)                            

4)                             

5)                                 

6)                               

7)        

8)        

9)        

10)     

11)     

12)     

13)     

3.Правила дифференцирования:

Константы можно выносить за знак производной:

 Производная суммы равна сумме производных:

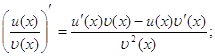
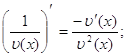
Пусть сложная функция,  и

Тогда:

9. Интегрирование, также как и операция дифференцирования , операция вычисления  пределов, является линейной; то есть, константы можно выносить за знак интеграла, и интеграл суммы функций равен сумме интегралов. Линейность операции интегрирования можно выразить формулой:

10. Таблица основных неопределенных интегралов:

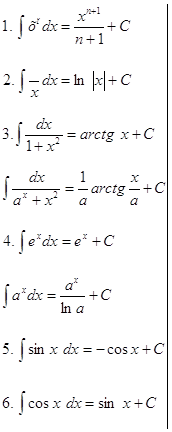
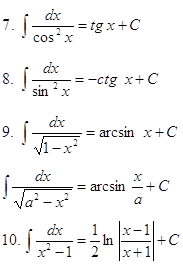
11).  при

11. Замена переменных (метод подстановки):

Если  Эта формула позволяет интегрировать произведения, одним из сомножителей которых служит сложная функция  

12. Интегрирование по частям: 

13. Интегрирование простейших дробей:

14. Если F(x)- первообразная, вычисляемая как неопределенный интеграл с С=0.