Контрольная работа: Высшая математика
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ РФ
НОУ ВПО «С.И.Б.У.П.»
Контрольная работа
по дисциплине «Высшая математика»
Вариант 13.
Выполнила студентка
Проверил:
Красноярск, 2008г.
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
A = B + C,
где B: работает только 1-й (2-й простаивает); C: работает только 2-й (1-й простаивает). Каждое из этих событий есть произведение 2 независимых событий:
B = D![]() ;
;
C = ![]() E,
E,
где
D, E
– события, состоящие в том, что 1-й и 2-й комбайны работают; ![]() ,
,
![]() -
противоположные им события, т.е. 1-й и 2-й комбайны не работают. Их
вероятности:
-
противоположные им события, т.е. 1-й и 2-й комбайны не работают. Их
вероятности:
P (D) = 0,8
P (E) = 0,6
P (![]() ) = 1 – P (D) = 1 – 0,8 = 0,2
) = 1 – P (D) = 1 – 0,8 = 0,2
P (![]() ) = 1 – P (E) = 1 – 0,6 = 0,4
) = 1 – P (E) = 1 – 0,6 = 0,4
По теоремам сложения и умножения вероятностей
P (A) = P (B) + P (C) = P (D) P (![]() ) + P (
) + P (![]() ) P (E) = 0,8 * 0,4 +
0,2 * 0,6 = 0,44
) P (E) = 0,8 * 0,4 +
0,2 * 0,6 = 0,44
Б) Данное событие (оба комбайна простаивают) есть произведение 2 независимых событий:
F = ![]()
![]()
По теореме умножения вероятностей
P (F)
= P (![]() )
P (
)
P (![]() )
= 0,2 * 0,4 = 0,08
)
= 0,2 * 0,4 = 0,08
Задание 2
Вероятность того, что пассажир опоздает к отправлению поезда, равна 0,01. Найти наиболее вероятное число опоздавших из 800 пассажиров и вероятность такого числа опоздавших.
Происходит n = 800 независимых испытаний, в каждом из которых данное событие (опоздание на поезд) происходит с вероятностью p = 0,01. Наиболее вероятное число наступлений события удовлетворяет неравенствам
np – q ≤ k < np + p,
где q = 1 – p = 1 – 0,01 = 0,99
800 * 0,01 – 0,99 ≤ k < 800 * 0,01 + 0,01
7,01 ≤ k < 8,01
k = 8
Так как n велико, p мала, соответствующую вероятность найдем по формуле Пуассона:
Pn (k)
= ![]() ,
,
где a = np = 800 * 0,01 = 8
P800 (8) = 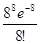 = 0,140
= 0,140
На двух автоматических станках производятся одинаковые изделия, даны законы распределения числа бракованных изделий, производимых в течение смены на каждом из них для первого и для второго.
X 0 1 2 Y 0 2
p 0,1 0,6 0,3 p 0,5 0,5
Составить закон распределения случайной величины Z = X + Y числа производимых в течение смены бракованных изделий обоими станками. Составить функцию распределения и построить ее график. Проверить свойство математического ожидания суммы случайных величин.
Величина Z может принимать значения:
0 + 0 = 0
0 + 2 = 2
1 + 0 = 1
1 + 2 = 3
2 + 0 = 2
2 + 2 = 4
Вероятности этих значений (по теоремам сложения и умножения вероятностей):
P (Z = 0) = 0,1 * 0,5 = 0,05
P (Z = 1) = 0,6 * 0,5 = 0,3
P (Z = 2) = 0,1 * 0,5 + 0,3 * 0,5 = 0,2
P (Z = 3) = 0,6 * 0,5 = 0,3
P (Z = 4) = 0,3 * 0,5 = 0,15
Закон распределения:
Z 0 1 2 3 4
p 0,05 0,3 0,2 0,3 0,15
Проверка:
∑ pi = 0,05 + 0,3 + 0,2 + 0,3 + 0,15 = 1.
Функция распределения
F (x)
= P (X
< x) = 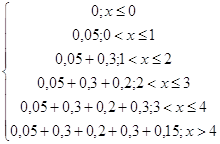 =
=
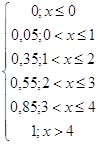
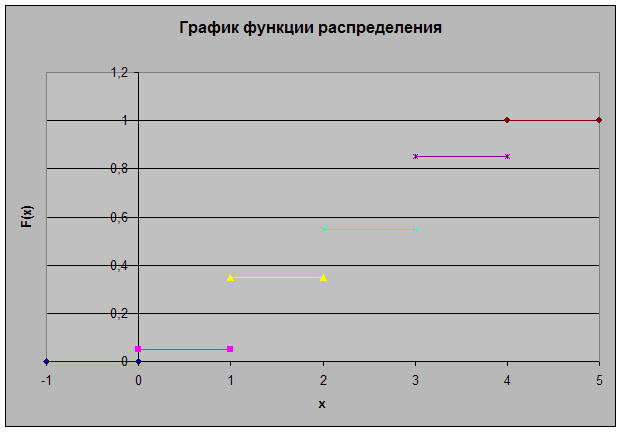
Математические ожидания:
M (x) = ∑ xipi = 0 * 0,1 + 1 * 0,6 + 2 * 0,3 = 1,2
M (y) = ∑ yipi = 0 * 0,5 + 2 * 0,5 = 1
M (z) = ∑ zipi = 0 * 0,05 + 1 * 0,3 + 2 * 0,2 + 3 * 0,3 + 4 * 0,15 = 2,2
M (z) = M (x) + M (y) = 1,2 + 1 = 2,2
Задание 4
Случайная величина X задана функцией распределения
F (x)
= 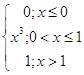
Найти: 1) вероятность попадания случайной величины X в интервал (1/3; 2/3); 2) функцию плотности распределения вероятностей f (x); 3) математическое ожидание случайной величины X; 4) построить графики F (x) и f (x).
1) Вероятность попадания случайной величины в интервал (a, b) равна
f (x) = F`(x) = 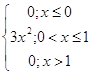
3) Математическое ожидание
M (X)
= ![]() =
= 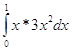 =
= 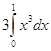 =
= ![]() = ¾ (14
– 04) = ¾
= ¾ (14
– 04) = ¾
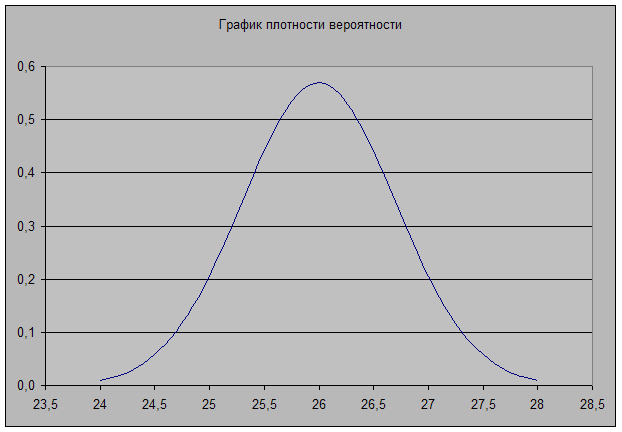
4) Графики:
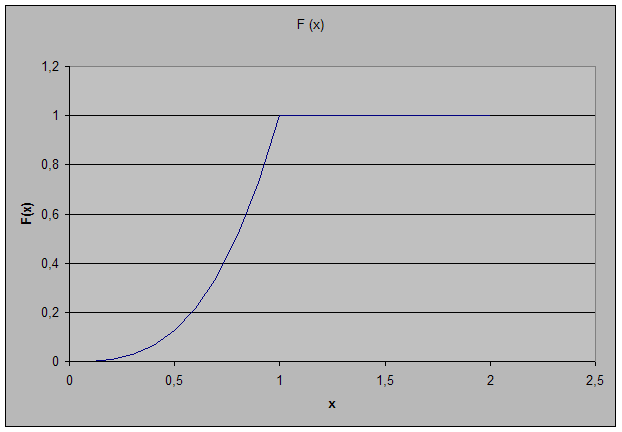
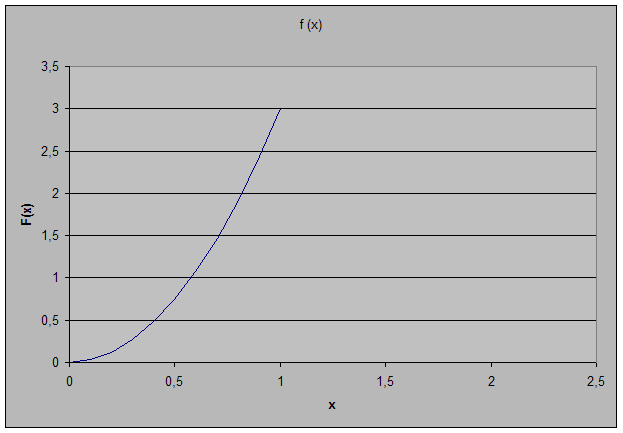
Задание 5
f (x)
= 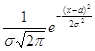 =
= 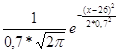 =
= 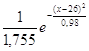
Б) Вероятность того, что нормальная величина примет значение из интервала (α; β), равна
P (α < X
< β) = ![]() -
- ![]() =
=
![]() -
- ![]() =
Ф (1,14) – Ф (-1,14) = 0,3735 + 0,3735 = 0,747
=
Ф (1,14) – Ф (-1,14) = 0,3735 + 0,3735 = 0,747
Значения
функции Лапласа Ф (x) = 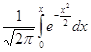 берем
из таблиц.
берем
из таблиц.
В) Вероятность того, что отклонение нормальной величины от математического ожидания не превышает ε, равна
P (|X
– a| < ε) = ![]()
P (|X
– 26| < 0,5) = ![]() = 2Ф (0,714) = 2 * 0,2611 =
0,5222
= 2Ф (0,714) = 2 * 0,2611 =
0,5222
СТАТИСТИКА
В задаче приведена выборка, извлеченная из соответствующей генеральной совокупности. Требуется: 1) по несгруппированным данным найти выборочную среднюю; 2) найти доверительный интервал для оценки неизвестного математического ожидания признака X генеральной совокупности (генеральной средней), если признак X распределен по нормальному закону; известны γ = 0,98 – надежность и σ = 200 – среднее квадратическое отклонение; 3) составить интервальное распределение выборки с шагом h = 200, взяв за начало первого интервала x1 = 700; 4) построить гистограмму частот; 5) дать экономическую интерпретацию полученных результатов.
Проведено выборочное обследования объема промышленного производства за 16 месяцев и получены следующие результаты (тыс. руб.):
750; 950; 1000; 1050; 1050; 1150; 1150; 1150; 1200; 1200; 1250; 1250; 1350; 1400; 1400; 1550
1) Выборочная средняя
![]() =
=
![]() = (750 +
950 + 1000 + 1050 + 1050 + 1150 + 1150 + 1150 + 1200 + 1200 + 1250 + 1250 +
1350 + 1400 + 1400 + 1550) / 16 = 18850 / 16 = 1178,1 тыс. руб.
= (750 +
950 + 1000 + 1050 + 1050 + 1150 + 1150 + 1150 + 1200 + 1200 + 1250 + 1250 +
1350 + 1400 + 1400 + 1550) / 16 = 18850 / 16 = 1178,1 тыс. руб.
2) Доверительный интервал
![]() -
- ![]() <
a <
<
a < ![]() +
+ ![]() ,
,
где Ф (t) = γ / 2 = 0,98 / 2 = 0,49. По таблице функции Лапласа находим: t = 2,32.
1178,1
- ![]() <
a <
1178,1 +
<
a <
1178,1 + ![]()
1178,1 – 116,3 < a < 1178,1 + 116,3
1061,8 < a < 1294,4 тыс. руб.
3) Подсчитаем границы интервалов:
x2 = x1 + h = 700 + 200 = 900 и т.д.
Подсчитаем частоты интервалов (т.е. количество значений объема производства, попавших в данный интервал). Интервальное распределение выборки:
Интервал |
Частоты |
| (700; 900) | 1 |
| (900; 1100) | 4 |
| (1100; 1300) | 7 |
| (1300; 1500) | 3 |
| (1500; 1700) | 1 |
4) Гистограмма частот:
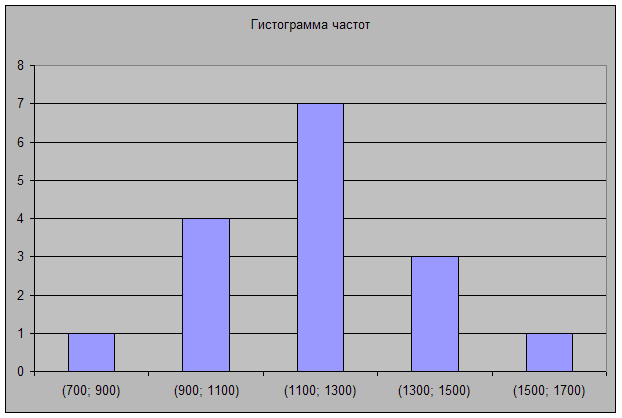
5) Экономическая интерпретация. Средний объем промышленного производства за 16 месяцев составил 1178,1 тыс. руб. С надежностью 0,98 можно утверждать, что средний объем производства находится в пределах от 1061,8 до 1294,4 тыс. руб. Наибольшее число месяцев (7) объем производства находился в интервале от 1100 до 1300 тыс. руб.
Задание 2
По корреляционной таблице требуется: 1) в прямоугольной системе координат построить эмпирические ломаные регрессии Y на X и X на Y, сделать предположение о виде корреляционной связи; 2) оценить тесноту линейной корреляционной связи; 3) составить линейные уравнения регрессии Y на X и X на Y, построить их графики в одной системе координат; 4) используя полученное уравнение, оценить ожидаемое среднее значение признака Y при заданном x = 98. Дать экономическую интерпретацию полученных результатов.
В таблице дано распределение 200 заводов по основным фондам X в млн. руб. и по готовой продукции Y в млн. руб.:
| y\x | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | ny |
| 12 | 4 | 4 | ||||||||
| 18 | 6 | 10 | 2 | 18 | ||||||
| 24 | 8 | 13 | 1 | 1 | 23 | |||||
| 30 | 4 | 7 | 9 | 3 | 4 | 2 | 29 | |||
| 36 | 1 | 2 | 3 | 12 | 4 | 8 | 30 | |||
| 42 | 1 | 3 | 18 | 24 | 1 | 47 | ||||
| 48 | 7 | 12 | 3 | 22 | ||||||
| 54 | 9 | 18 | 27 | |||||||
| nx | 10 | 23 | 24 | 14 | 19 | 26 | 41 | 22 | 21 | n = 200 |
1) Расчетная таблица:
|
X Y |
20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | ny | yny | y2 | y2ny | ∑xnxy |
Усл. ср. |
| 12 | 4 | 4 | 48 | 144 | 576 | 80 | 20,0 | ||||||||
| 18 | 6 | 10 | 2 | 18 | 324 | 324 | 5832 | 500 | 27,8 | ||||||
| 24 | 8 | 13 | 1 | 1 | 23 | 552 | 576 | 13248 | 870 | 37,8 | |||||
| 30 | 4 | 7 | 9 | 3 | 4 | 2 | 29 | 870 | 900 | 26100 | 1470 | 50,7 | |||
| 36 | 1 | 2 | 3 | 12 | 4 | 8 | 30 | 1080 | 1296 | 38880 | 1900 | 63,3 | |||
| 42 | 1 | 3 | 18 | 24 | 1 | 47 | 1974 | 1764 | 82908 | 3500 | 74,5 | ||||
| 48 | 7 | 12 | 3 | 22 | 1056 | 2304 | 50688 | 1940 | 88,2 | ||||||
| 54 | 9 | 18 | 27 | 1458 | 2916 | 78732 | 2610 | 96,7 | |||||||
| nx | 10 | 23 | 24 | 14 | 19 | 26 | 41 | 22 | 21 | 200 | 7362 | 296964 | 12870 | ||
| xnx | 200 | 690 | 960 | 700 | 1140 | 1820 | 3280 | 1980 | 2100 | 12870 | |||||
| x2 | 400 | 900 | 1600 | 2500 | 3600 | 4900 | 6400 | 8100 | 10000 | ||||||
| x2nx | 4000 | 20700 | 38400 | 35000 | 68400 | 127400 | 262400 | 178200 | 210000 | 944500 | |||||
| ∑ynxy | 156 | 528 | 630 | 444 | 672 | 1020 | 1692 | 1104 | 1116 | 7362 | |||||
| ∑xynxy | 3120 | 15840 | 25200 | 22200 | 40320 | 71400 | 135360 | 99360 | 111600 | 524400 | |||||
|
Усл. ср. |
15,6 | 23,0 | 26,3 | 31,7 | 35,4 | 39,2 | 41,3 | 50,2 | 53,1 |
Подсчитаем условные средние:
![]() x
= 20 =
x
= 20 = ![]() =
(12 * 4 + 18 * 6) / 10 = 15,6 и т.д.
=
(12 * 4 + 18 * 6) / 10 = 15,6 и т.д.
![]() y
= 12 =
y
= 12 = 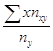 =
20 * 4 / 4 = 20,0 и т.д.
=
20 * 4 / 4 = 20,0 и т.д.
Эмпирические ломаные регрессии:
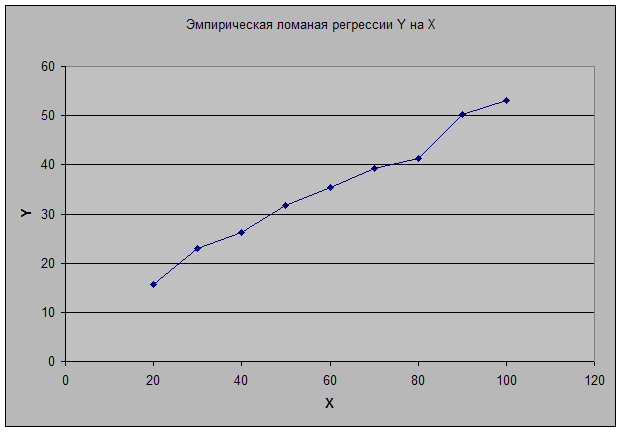
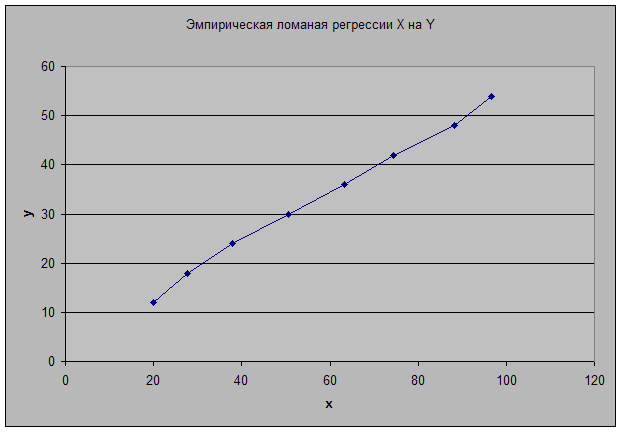
Эмпирические линии регрессии близки к прямым. Можно сделать предположение о линейном характере связи между величиной основных фондов и готовой продукцией.
2) Выборочные средние:
![]() =
= ![]() = 12870 / 200
= 64,35
= 12870 / 200
= 64,35
![]() =
= ![]() = 7362 / 200 =
36,81
= 7362 / 200 =
36,81
Выборочные средние квадратические отклонения
σx
= ![]() =
= ![]() =
24,12
=
24,12
σy
= 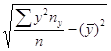 =
= ![]() =
11,39
=
11,39
Выборочный коэффициент корреляции
r = 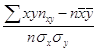 =
=
![]() = 0,922
= 0,922
3) Уравнение линейной регрессии Y по X:
![]() x
-
x
- ![]() = r
= r![]() (x
-
(x
- ![]() )
)
![]() x
– 36,81 = 0,922 *
x
– 36,81 = 0,922 * ![]() (x
– 64,35)
(x
– 64,35)
![]() x
= 0,435x + 8,786
x
= 0,435x + 8,786
Уравнение линейной регрессии X по Y:
![]() y
-
y
- ![]() =
r
=
r![]() ( y
-
( y
- ![]() )
)
![]() y
– 64,35 = 0,922 *
y
– 64,35 = 0,922 * ![]() (y
– 36,81)
(y
– 36,81)
![]() y
= 1,951y – 7,452
y
= 1,951y – 7,452
Графики:
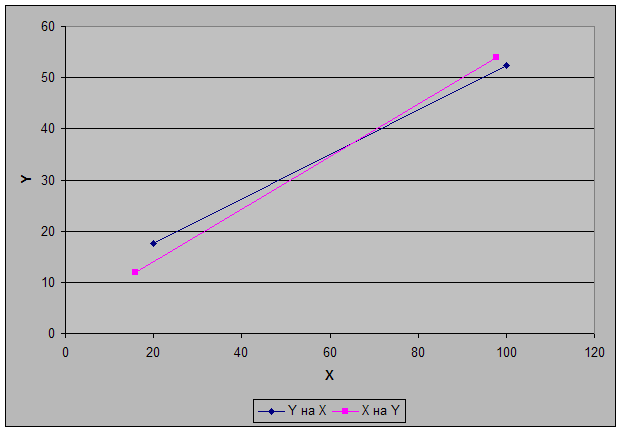
4) Ожидаемое среднее значение Y при X = 98:
![]() x
= 98 = 0,435 * 98 + 8,786 = 51,5 млн. руб.
x
= 98 = 0,435 * 98 + 8,786 = 51,5 млн. руб.
Экономическая интерпретация. Связь между величиной основных фондов и готовой продукций прямая и очень тесная: коэффициент корреляции положителен и близок к 1. При увеличении основных фондов на 1 млн. руб. готовая продукция возрастает в среднем на 0,435 млн. руб. При увеличении готовой продукции на 1 млн. руб. основные фонды возрастают в среднем на 1,951 млн. руб. При величине основных фондов 98 млн. руб. ожидаемое среднее значение готовой продукции 51,5 млн. руб.
Задание 3
Даны эмпирические значения случайной величины. Требуется: 1) выдвинуть гипотезу о виде распределения; 2) проверить гипотезу с помощью критерия Пирсона при заданном уровне значимости α = 0,05. За значения параметров a и σ принять среднюю выборочную и выборочное среднее квадратичное отклонение, вычисленные по эмпирическим данным.
В таблице дано распределение дохода от реализации некоторого товара:
| 8-12 | 12-16 | 16-20 | 20-24 | 24-28 | 28-32 |
| 6 | 11 | 25 | 13 | 4 | 1 |
1) Вычислим середины интервалов дохода:
xi = (8 + 12) / 2 = 10 и т.д.
Расчетная таблица:
| № | xi | ni | xini |
xi - |
(xi - |
(xi - |
| 1 | 10 | 6 | 60 | -8,067 | 65,071 | 390,4 |
| 2 | 14 | 11 | 154 | -4,067 | 16,538 | 181,9 |
| 3 | 18 | 25 | 450 | -0,067 | 0,004 | 0,1 |
| 4 | 22 | 13 | 286 | 3,933 | 15,471 | 201,1 |
| 5 | 26 | 4 | 104 | 7,933 | 62,938 | 251,8 |
| 6 | 30 | 1 | 30 | 11,933 | 142,404 | 142,4 |
| Сумма | 60 | 1084 | 1167,7 |
Выборочное среднее
![]() =
=
![]() = 1084 /
60 = 18,067
= 1084 /
60 = 18,067
Выборочное среднее квадратическое отклонение
s = 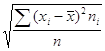 =
= ![]() = 4,412
= 4,412
Выдвигаем гипотезу о нормальном распределении.
2) Расчетная таблица для применения критерия Пирсона:
| i | xi | Частоты ni |
ui = (xi - |
φ (ui) = |
Теорет. частоты ni` = nh φ (ui) / s | ni - ni` | (ni - ni`)2 | (ni - ni`)2 / ni` |
| 1 | 10 | 6 | -1,829 | 0,0750 | 4,1 | 1,9 | 3,7 | 0,9 |
| 2 | 14 | 11 | -0,922 | 0,2609 | 14,2 | -3,2 | 10,2 | 0,7 |
| 3 | 18 | 25 | -0,015 | 0,3989 | 21,7 | 3,3 | 10,9 | 0,5 |
| 4 | 22 | 13 | 0,892 | 0,2681 | 14,6 | -1,6 | 2,5 | 0,2 |
| 5 | 26 | 4 | 1,798 | 0,0792 | 4,3 | -0,3 | 0,1 | 0,0 |
| 6 | 30 | 1 | 2,705 | 0,0103 | 0,6 | 0,4 | 0,2 | 0,3 |
| Сумма | 60 | 59,4 | 2,7 |
Наблюдаемое значение
χн2 = ∑ (ni - ni`)2 / ni` = 2,7
Критическое значение (из таблиц при уровне значимости α = 0,05 и числе степеней свободы k = 6 – 3 = 3)
χкр2 = 7,8
Так как χн2 < χкр2, гипотезу о нормальном распределении принимаем.