Реферат: Граничні теореми теорії ймовірностей

Міністерство освіти і науки України

Приватний вищий навчальний заклад

Європейський університет

Запорізька філія

Реферат

Граничні теореми теорії ймовірностей

з дисципліни: Теорія ймовірностей та математична статистика

Запоріжжя,

2007р.

Теорема Бернуллі. Нехай імовірність появи події А в кожному із п незалежних повторних випробувань дорівнює р, т - число появ події А (частота події) в п випробуваннях. Тоді

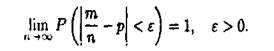
Доведення. Частість можна розглядати як невід'ємну випадкову величину. Знайдемо її математичне сподівання

Отже, необхідно оцінити імовірність відхилення випадкової величинивід її математичного сподівання. Для цього знайдемо дисперсію цієї випадкової величини

За нерівністю Чебишова одержимо

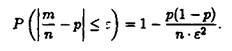
Звідси граничним переходомодержуємо (4), що й треба було довести.

Теорема Чебишова. Нехай - послідовність попарно незалежних випадкових величин, які задовольняють умовам

для усіх t = 1,2,..., п.

Тоді

Доведення. Знайдемо математичне сподівання та дисперсіюсередньої випадкових величин, тобто

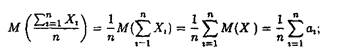
Застосуємо для випадкової величини нерівність Чебишова (2)

Границя цієї імовірності при  дорівнює одиниці, тобто рівність (5) доведено.

Центральна гранична теорема. Нехай задана послідовність незалежних однаково розподілених випадкових величин

Розглянемо випадкову величинуТоді

Прифункція розподілу

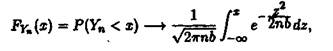
тобто сумабуде розподілена за нормальним законом з математичним сподіванням 0 та дисперсією

Для доведення цієї теореми треба знайти границю характеристичної функції, побудованої для нормованої випадкової величини

Наслідок. При розподіл суми однаково розподілених випадкових величин мало відрізняється від нормального розподілу.

Теорема Ляпунова. Нехай задана послідовність незалежних випадкових величин таких, що

Побудуємо суму випадкових величин  ПозначимоЯкщо виконується умова рівномірної малості величин, що утворюють суму

то сумабуде розподіленою нормально з математичним сподіваннямта дисперсією

Доведення цієї теореми досить складне, але відмітимо, що у випадку, колиможна розглядати випадкові величини Величинибудуть задовольняти умову теореми Ляпунова.

Приклад 2. Скільки додатків треба взяти у теоремі Чебишова, щоб з надійністю 96% і точністю до 0.01 виконувалась наближена рівність

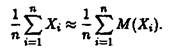
Розв'язок. В цьому прикладі є = 0.01. Щоб одержати надійність 96% згідно формули (6) достатньо підібрати таке п, яке задовольняє нерівність

Зауваження 1. Приклад 2 показує, що навіть у випадку не дуже великих точності та надійності, треба брати значну кількість додатків (п - досить велике число). Це означає, що оцінки, одержані з використанням нерівності (6), - завищені. Більш точні оцінки можна одержати за допомогою теореми Ляпунова.

Список використаної літератури

1.    Барковський В.В., Барковська Н.В., Лопатін О.К. теорія ймовірностей та математична статистика. – К.: ЦУЛ, 2002. – 448с.

2.    Гмурман В.Е. теория вероятностей и математическая статистика. – М.: Высшая школа, 1980.

3.    Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 1975.

4.    Гнеденко Б.В. Курс теории вероятностей. – М.: наука, 1988.

5.    Леоненко М.М., Мішура Ю.С. та ін. Теоретико-ймовірностні та статистичні методи в економетриці та фінансовій математиці. – К.: Інформтехніка, 1995.