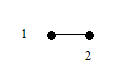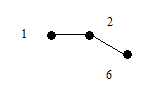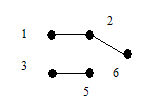Реферат: Деревья и их свойства (частный вид графов)

Учреждение образования

«Белорусский государственный университет

информатики и радиоэлектроники»

РЕФЕРАТ

на тему:

«ДЕРЕВЬЯ И ИХ СВОЙСТВА (ЧАСТНЫЙ ВИД ГРАФОВ)»

Минск, 2008

Рассмотрим частный вид графов, широко используемых, например, в теории электрических цепей, химии, вычислительной технике и в информатике.

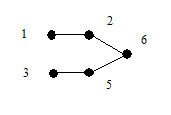
Определение 1. Деревом называется связный граф, не содержащий циклов. Любой (в том числе несвязный) граф без циклов называется ациклическим. Несвязный граф, каждая компонента связности которого является деревом, называется лесом. Можно сказать, что деревья являются компонентами леса. На рис.1 изображены два дерева G1, G2 и лес G3.

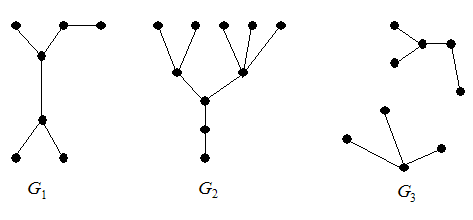
Рис.1

Сформулируем основные свойства деревьев. Сделаем это в виде совокупности утверждений, которые эквивалентны между собой (т.е. из любого утверждения следует любое другое) [].

Теорема 1. Пусть G(X, E) – неориентированный граф с p вершинами и q ребрами. Тогда следующие утверждения эквивалентны.

1 . G есть дерево.

2 . Любые две различные вершины x и y графа G соединены единственной простой цепью.

3 . G – связный граф, утрачивающий это свойство при удалении любого из его ребер.

4 . G – связный граф и p = q + 1.

5 . G – ациклический граф и p = q + 1.

6 . G – ациклический граф, причем если любые две его вершины x и y соединить ребром e, то в полученном графе будет ровно один простой цикл.

Для доказательства теоремы достаточно доказать следующую цепочку следствий: 1 Þ 2 Þ 3 Þ 4 Þ 5 Þ 6 Þ 1 , так как это означает, что из любого утверждения 1 – 6 выводится любое другое.

1 Þ2 . Так как граф связен, то любые две его вершины можно соединить простой цепью. Пусть m1 и m2 - две различные простые цепи, соединяющие вершины x и y. Если цепи m1 и m2 не имеют общих вершин, за исключением вершин x и y, то есть простой цикл. Предположим, что цепи m1 и m2 имеют общие вершины, отличные от x и y. Пусть z – первая из таких вершин при движении от вершины x к вершине y и пусть m1(x, z) и m2(x, z) – части цепей m1 и m2, взятые от вершины x до вершины z. Тогда  - простой цикл. Это противоречит тому, что граф ацикличен, и поэтому m1=m2, т.е. утверждение 2 доказано.

2 Þ3 . Граф G – связен, поскольку любые две его различные вершины x и y соединены простой цепью. Возьмем некоторое ребро графа e = (x, y). Согласно 2 простая цепь m={e} между вершинами x и y единственна. Если ребро e удалить, то вершины x и y будет невозможно соединить простой цепью, и полученный граф будет несвязным. Утверждение 3 доказано.

3 Þ4 . По условию 3 граф связен. Соотношение p = q + 1 докажем по индукции. Если граф имеет две вершины и удовлетворяет 3 , то он выглядит так:

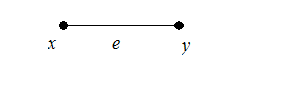
В этом случае p = 2, q = 1 и соотношение p = q + 1 выполняется. Предположим теперь, что соотношение верно для всех графов, удовлетворяющих 3 и имеющих меньше, чем p вершин, и докажем его для графа G с p вершинами. Удалим из графа G произвольное ребро e. Тогда новый граф G´ будет несвязным и будет состоять из двух связных компонент G1 и G2. По предположению индукции имеем

p1 = q1 + 1, p2 = q2 + 1,

где pi – число вершин компоненты Gi, qi – число ее ребер. Следовательно,

p = p1 + p2, q = q1 + q2 + 1,

поэтому p = q1 + q2 + 2 = q + 1, и свойство 4 доказано.

4 Þ5 . Предположим, что граф G, удовлетворяющий 4 , имеет простой цикл m длиной l ³ 1. Этот цикл содержит l вершин и l ребер. Для любой из p - l вершин, не принадлежащих циклу m, существует инцидентное ей ребро, ле­жащее на кратчайшей цепи ( т.е. цепи минимальной длины), идущей от данной вершины к некоторой вершине цикла m. Все такие ребра попарно различны. Если вершины x1 и x2 инцидентны одному такому ребру e, то e = (x1, x2), и кратчайшая цепь m1 для вершины x1 проходит через вершину x2, а кратчайшая цепь m2 для вершины x2 проходит через вершину x1 (рис. 2). Это противоречит тому, что цепи m1 и m2 – кратчайшие. Общее число ребер q в графе G в этом случае не меньше, чем l + p – l = p, т.е. q ³ p, что противоречит соотношению p = q + 1. Отсюда следует, что G – ациклический граф, и утверждение 5 доказано.

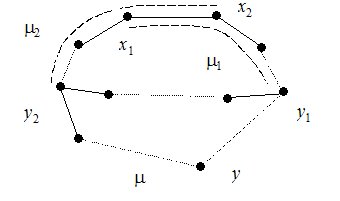
Рис. 2

5 Þ6 . Так как G – ациклический граф, то каждая его компонента связности Gi (i = 1, 2, …, k) является деревом. Для каждой компоненты Gi имеем в соответствии с 5 pi = qi + 1, откуда 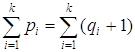, т.е. p = q + k. С другой стороны, p = q + 1, поэтому k = 1, т.е. граф G связен. Таким образом, G – дерево. Тогда (см. 2 ) любые две различные вершины x и y графа G соединены единственной простой цепью. Если добавить ребро между несмежными вершинами x и y, то оно образует с указанной цепью единственный простой цикл. Утверждение 6 доказано.

6 Þ1 . По условию 6 G – ациклический граф. Если граф G не является связным, то возьмем вершины x и y из различных компонент связности графа G и соединим их ребром e. Построенный граф  является, как и граф G, ациклическим. Это противоречит свойству G, поэтому G – связный граф, и свойство 1 доказано. Таким образом, доказана и теорема 1.

Определение, аналогичное дереву, можно ввести и для орграфа.

Определение 2. Орграф G(X, E) называется прадеревом или ориентированным деревом, растущим из корня x0, при следующих условиях:

1 . Неориентированный граф G', соответствующий графу G, является деревом.

2 . Единственная простая цепь между x0 и любой другой вершиной x графа G' является путем в орграфе G, идущим из вершины x0 в вершину x.

На рис. 3 изображено ориентированное дерево.

Рис. 3

В неориентированном графе G(X, E) вершина x называется концевой или висячей, если d(x) = 1, т.е. если этой вершине инцидентно единственное ребро e. Это ребро также называется концевым или висячим. С висячими вершинами связана следующая теорема.

Теорема 2. В любом дереве G(X, E) с p ³ 2 вершинами имеется не менее двух концевых вершин.

Доказательство. Пусть q – число ребер дерева G. В силу теоремы 1 p = q + 1. Кроме того, из теоремы 1.1 имеем

.

Таким образом, получаем

.                        (1)

Предположим, что x0 – единственная концевая вершина в дереве G. Тогда d(x0) = 1, d(x) ³ 2, если x ¹ x0. Отсюда

.                    (2)

Неравенство (2) противоречит (1), поэтому либо концевых вершин нет, либо их по крайней мере две. Если концевых вершин в G нет, то d(x) ³ 2 для всех xÎX. Тогда

.                               (3)

Неравенство (3) тоже противоречит (1). Отсюда следует, что концевых вершин в G две или больше. Теорема доказана.

Важным является вопрос о том, сколько существует деревьев с заданным числом вершин. Для деревьев с помеченными вершинами (например пронумерованными) или для помеченных деревьев ответ на этот вопрос дает следующая теорема.

Теорема 3. (А. Кэли, 1897 г.). Число помеченных деревьев с p вершинами равно pp-2.

Доказательство. Пусть G(X, E) – дерево с p помеченными вершинами. Для простоты предположим, что вершины пронумерованы в произвольном порядке числами 1, 2, …, p. Рассмотрим способ, позволяющий однозначно закодировать дерево G.

В соответствии с теоремой 2 дерево G имеет концевые вершины. Пусть x1 – первая концевая вершина в последовательности 1, 2, …, p и пусть e1 = (x1, y1) – соответствующее концевое ребро. Удалим из дерева вершину x1 и ребро e1. Получим новое дерево G1 с числом вершин p - 1. Найдем теперь пер­­вую концевую вершину x2 дерева G1 в последовательности вершин 1, 2, … …, p из множества {1, 2, …, p }\{x1}, далее возьмем концевое ребро e2 = (x2, y2) и удалим из G1 x2 и e2. Эту процедуру последовательно повторяем. Через (p - 2) шага остается дерево из двух вершин xp-1, yp-1 и одного ребра ep-1 = (xp-1, yp-1). Рассмотрим последовательность вершин

s(G) = {y1, y2, …, yp-2}.

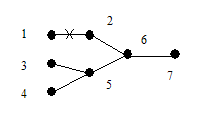
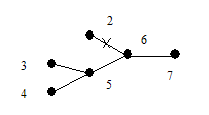
Очевидно, что по данному дереву последовательность строится однозначно. Покажем теперь, что по данной последовательности вершин s (G) дерево G можно восстановить однозначно. В последовательности 1, 2, …, p существуют вершины, не принадлежащие s (G). Выберем первую из них x1 и построим ребро e1 = (x1, y1). Затем удалим x1 из последовательности 1, 2, …, n и y1 удалим из s(G). Аналогичным образом построим ребро e2 = (x2, y2). Продолжая этот процесс, мы однозначно восстановим дерево G. Рассмотрим пример.

Построение кода	Восстановление
s(G)	s(G) и список вершин
(2,6,5,5,6)  1,2,3,4,5,6,7   (2)
(6,5,5,6)  2,3,4,5,6,7   (2,6)
(5,5,6)  3,4,5,6,7   (2,6,5)
(5,6)  4,5,6,7   (2,6,5,5)
(6)  5,6,7   (2,6,5,5,6)

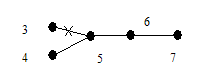
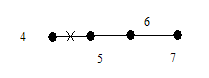
Рассмотренный пример позволяет отметить следующие две особенности:

1 В списке s(G) вершины могут повторяться.

2 . При восстановлении дерева последнее ребро соединяет вершину yp-2 и оставшуюся в списке 1, 2, …, p вершину не равную yp-2.

Итак, существует взаимно однозначное соответствие между множеством помеченных деревьев с p вершинами и множеством последовательностей вершин s(G). Число таких последовательностей равно, очевидно, pp-2, что и требовалось доказать.

Отметим, что среди pp-2 помеченных деревьев с p вершинами могут быть и изоморфные.

Определение 3. Подграф G1(X1, E1) неориентированного графа G(X, E) называется каркасом, или остовным деревом графа G, если G1 – дерево и X = X1.

Теорема 4. Граф G(X, E) тогда и только тогда обладает каркасом, когда он связен.

Доказательство. Необходимость этого очевидна. Докажем достаточность. Пусть G(X, E) – связный граф. Выясним, есть ли в графе G такое ребро, удаление которого не нарушает связности графа G. Если таких ребер нет, то граф есть дерево в соответствии с теоремой 1. Если же такое ребро, например e, существует, то выбросим его и придем к графу G1(X, E\{e}). Затем указанную процедуру проделываем с графом G1 и т.д. Через конечное число шагов будет построен, очевидно, каркас графа G. Теорема доказана.

Доказательство теоремы дает алгоритм построения некоторого каркаса в связном графе. Однако связный граф может иметь несколько каркасов, поэтому естественно поставить задачу выбора каркаса, удовлетворяющего дополнительным условиям.

Определение 4. Графом с нагруженными ребрами (нагруженным графом) называется неориентированный граф G(X, E), каждому ребру eÎE которого поставлено в соответствие число m(e) ³ 0, называемое весом или длиной ребра e.

Аналогично можно определить нагруженный орграф.

Поставим задачу нахождения такого каркаса G1(X, E1) в нагруженном графе G(X, E), для которого сумма

минимальна. Каркас с таким свойством называется минимальным каркасом. В соответствии с теоремой 4 каждый нагруженный связный граф обладает минимальным каркасом. Эта задача возникает при проектировании линий связи и электропередач, дорог, трубопроводов и т.п., когда требуется соединить системой каналов связи заданные узлы так, чтобы любые два узла были связаны (возможно, через другие узлы), а общая длина каналов связи была минимальной; при этом узлы можно считать вершинами нагруженного графа, весам ребер которого соответствует длина возможного канала связи между соответствующими узлами. Тогда искомая сеть каналов будет минимальным каркасом этого графа.

Алгоритм построения минимального каркаса

Пусть G(X, E) - связный нагруженный граф с p вершинами.

Шаг 1 . В качестве первого ребра искомого минимального каркаса выбираем ребро e1 с наименьшим весом m(e1). Если таких ребер несколько, то берем любое из них.

Шаг 2 . В качестве второго ребра берем ребро e2 из множества E\{e1}, имеющее наименьший вес m(e2), и такое, что множество {e1, e2} не содержит простых циклов. Если таких ребер несколько, то берем любое из них.

Шаг 3 . В качестве третьего ребра выбираем такое ребро e3 из множества E\{e1, e2}, которое имеет наименьший вес m(e2) и для которого множество {e1, e2, e3} не содержит простых циклов. Если таких ребер несколько, берем любое из них.

Указанный процесс повторяется и через некоторое число k шагов дает множество E = {e1, e2, …, ek}, к которому нельзя добавить ребро без появления цикла. Подграф G1(X, E1) и является минимальным каркасом графа G(X, E).

Обоснование алгоритма

В силу свойства 6 из теоремы 1 построенный подграф G1(X, E1) является деревом, поэтому k = p –1. Доказательство минимальности каркаса G1(X, E1) разобьем на два этапа. Пусть сначала G(X, E) – полный граф, у которого веса всех ребер различны, и пусть G2(X, E2) – минимальный каркас графа G. Если E2 ¹ E1, то рассмотрим el – первое из ребер множества E1, не принадлежащее E2. В графе  в силу свойства 6 теоремы 1 существует единственный простой цикл m. Цикл m содержит ребро e0ÏE1. Граф G3(X, E3), где , не содержит циклов и имеет n – 1 ребро, поэтому он является деревом. Множество {e1, e2, …, el-1, e0} содержится в E2 и поэтому не содержит циклов. Тогда в силу рассмотренного выше алгоритма m(e0) > m(el). Отсюда следует, что суммарный вес дерева G3(X, E3) меньше веса дерева G2(X, E2). Это противоречит минимальности каркаса G2, поэтому E2 = E1 и G1(X, E1) – единственный минимальный каркас графа G.

Пусть теперь G(X, E) – произвольный нагруженный связный граф. Если m(e1) = m(e2), то сделаем замену

m(e1) ® m'(e1) = m(e1) + e,

m(e2) ® m'(e2) = m(e2) + 2e,

взяв такое e, чтобы сохранились соотношения весов m(e1) и m(e2) с другими весами. Сделаем граф G полным, добавив такие ребра di, что . В полученном графе единственным минимальным каркасом будет каркас, полученный с помощью рассмотренного алгоритма. Легко видеть, что этот каркас будет минимальным и в исходном графе G(X, E).

На рис.4 изображены нагруженный граф G и его минимальный каркас G1.

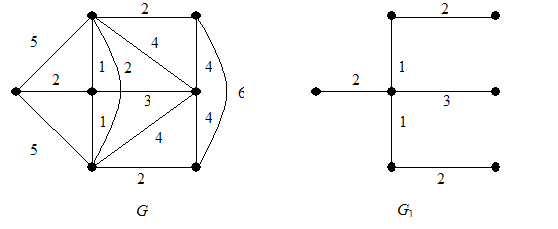
Рис. 4

ЛИТЕРАТУРА

1.         Белоусов А.И., Ткачев С.Б. Дискретная математика: Учебник для ВУЗов / Под ред. В.С. Зарубина, А.П. Крищенко.– М.: изд-во МГТУ им. Н.Э. Баумана, 2001.– 744 с. (Сер. Математика в техническом университете; Вып XIX).

2.         Горбатов В.А. Фундаментальные основы дискретной математики. Информационная математика.– М.: Наука, Физматлит, 2000.– 544 с.– ISBN 5-02-015238-2.