Курсовая работа: Конструкция склада минеральных удобрений
Пермский государственный технический университет
Строительный факультет
Кафедра строительных конструкций
Курсовой проект
Выполнил: ст. гр. ПГС – 07
Кузнецов А.Л.
Проверил: Осетрин А.В.
Пермь, 2009 г.
1. Расчет плиты покрытия
1.1 Исходные данные
Уклон кровли 1 : 3
Материал обшивок панелей - кровельные щиты ель 2 сорта
Шаг несущих конструкций - 3,0м
Шаг прогонов - 2м
Район строительства - г. Пермь
Условия эксплуатации - В2
а =33°41'24"
1.2 Расчёт конструкции не утепленного покрытия
Расчёт деревянного щита покрытия.
А. постоянные нагрузки
q us = г . д = 6000 · 0,05 = 300 Н/м2
где г = 6000 - плотность древесины ели
д= 0,05 - толщина щита
Б. временные нагрузки Снеговая нагрузка
S = So · м = 3200 · 0,75 = 2400 Н/ м2
So = 3200 Н/м 2 - нормативное значение веса снегового
покрова (для V снегового района ) -где м – коэф. перехода от веса снегового покрова на земле к снеговой нагрузке на покрытии
![]() =0,75
=0,75
Ветровая нагрузка действует перпендикулярно плоскости щита и находится по формуле:
wm = w0 · kc
w0 = 300 Н/м2
k = 0,65 + ![]() · 8 = 0,81 (при h = 18м)
· 8 = 0,81 (при h = 18м)
Сe = 0,2 + ![]() · 13,69 = 0,3369
· 13,69 = 0,3369
wm = 300 · 0,81· 0,3369 = 81, 87 Н/см2
1.3 Сбор нагрузок
| Нормативная Н/м2 | Коэф. Надежн. | Расчетная Н/м2 | |
| Постоянные | |||
| Масса щита покрытия | 300 | 1,1 | 330 |
| Временные | |||
|
Снеговая, ветровая |
1500 81,87 |
1,6 1,4 |
2400 114,62 |
| Итого: | 1881,87 | 2814,62 |
Расчетные погонные нагрузки
Собственный вес щита
q 1us = q us ∙ cosб ∙ B = 330 ∙ 0,832 ∙ 1 = 274,58 Н/м
Снеговая нагрузка
Sp S ∙ cos 2б ∙ B = 2400∙0,692∙1= 1660,08 Н/м
Ветровая нагрузка
Wp = Wm ∙ b = 186,2∙ 1 = 114,62 Н/м
1.4 Статический расчет щита
Щит рассчитывается по схеме 2-х пролетной балки
Расчетные сочетания нагрузок
Собственный вес+ снеговая нагрузка
q p1 = (q us +Sp) = 274,58 + 1660,08 = 1934,66 Н/м
2. Собственный вес + снеговая нагрузка + ветровая нагрузка
q p1 = q us + (W p + Sp) ∙ = 274,58 + (1660,08+114,62) ∙ 0,9 = 1871,81 Н/м
c∙k = 0,9
Максимальный изгибающий момент
M1 = ![]() =
= ![]() = 967,33 Н∙м
= 967,33 Н∙м
M11 = ![]() =
= ![]() = 935,91 Н∙м
= 935,91 Н∙м
1.5 Конструктивный расчет щита
Расчетные характеристики материала.
Расчет характеристик материала
Ru1 = 1300 ∙ 0,977 = 1275 H/см2
- Ru Расчетное сопротивление древесины на изгиб 1300 Н/см2
2. Ru11 = 1300 ∙ 0,977 ∙ 1,2 = 1530 Н/см2
1,2 – коэффициент кратковременной ветровой нагрузки
Требуемый момент ≥
W1 ≥ ![]() = 75,87 см3
= 75,87 см3
W11 ≥ ![]() = 61,17 см3
= 61,17 см3
W = ![]() = ( b = min 32мм)
= ( b = min 32мм)
Требуемая ширина досок (при ширине 1м)
W = ![]() =
= ![]() = 104,17 см3
= 104,17 см3
Нормативное напряжение.
у = ![]() = 893,38 Н/см2 < Ru = 1530
Н/см2
= 893,38 Н/см2 < Ru = 1530
Н/см2
Относительный прогиб при первом сочетании нагрузок.
qн = (300∙ 0,832 + 2400 ∙ 0,692) ∙ 1 = 1910,4 Н/м
I = ![]() = 130,21 см4
= 130,21 см4
![]() =
= ![]() ∙
∙ ![]() = 2,13 / 384
= 2,13 / 384![]() ∙
∙ ![]() =
= ![]() <
< ![]() =
= ![]()
2. Расчет разрезного прогона
2.1 Сбор нагрузок на прогон
q пр = 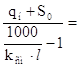 108,247 Н/м2
108,247 Н/м2
| Нормативная Н/м2 | Коэф. Надежн. | Расчетная Н/м2 | |
| Постоянные | |||
| Масса щита покрытия | 300 | 1,1 | 330 |
| Масса прогона | 108,247 | 1,1 | 119,075 |
| Временные | |||
| Снеговая | 1248,08 | 1,6 | 1990,92 |
| Итого: | 1656,32 | 2445,99 |
Погонные нагрузки при шаге прогонов 2м
qн = 1656,32 ∙ 2 = 3312,64 Н/м
qр = 2445,99 ∙ 2 = 4891,98 Н/м
2.2 Статический расчет прогона
Прогон работает как балка на 2-х опорах, в условиях косого изгиба. Расчетный пролет прогона
lр = ![]() = 300 –
= 300 –![]() = 285 см
= 285 см
Максимальный изгибающий момент.
М = ![]() =
= ![]() = 4966,89 Н∙м
= 4966,89 Н∙м
Составляющие моменты относительно главных осей сечения
Мх = М ∙ cos б = 4966,89 ∙ 0,832 = 4132, 45 Н∙м
Му = М ∙ sin б = 4966,89 ∙ 0,555 = 2756, 62 Н∙м
2.3 Конструктивный расчет прогона
Проектируем прогон прямоугольного сечения. Минимальные размеры поперечного сечения прогона при косом изгибе получаются при отношении сторон:
з = ![]() =
= ![]() =
= ![]() = 1,225
= 1,225
Требуемый момент сопротивления сечения
Wтр = ![]() =
= ![]() = 577,64 см3
= 577,64 см3
Требуемая высота сечения.
hтр = ![]() = 16,19 см
= 16,19 см
b= ![]() см
см
Принимаем сечение прогона 15,0 х 15,0 х 300 см
Геометрическая характеристика сечения
Wx = ![]() = 562,5 см3
= 562,5 см3
Ix = ![]() = 4218,75 см4
= 4218,75 см4
Проверка нормальных напряжений
у = ![]() +
+ ![]() =
= ![]() +
+ ![]() = 1224,71<Ru = 1300 Н/см2
= 1224,71<Ru = 1300 Н/см2
Проверка прогиба прогона при косом изгибе от нормативных нагрузок
fx= ![]() =
=
fy= ![]() =
=
f= ![]() = 0,363 <
= 0,363 < ![]() = 1,5 см
= 1,5 см
3. Расчет арки
3.1 Сбор нагрузок
Постоянные нагрузки
| Нормативная Н/м2 | Коэф. Надежн. | Расчетная Н/м2 | |
| Постоянные | |||
| Масса покрытия | 300 | 1,1 | 330 |
| Масса прогона | 108,247 | 1,1 | 119,075 |
| Масса арки | 545,51 | 1,1 | 600,06 |
| Итого: | 953,76 | 1049,135 |
qпр = 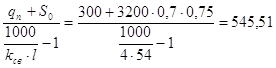 Н/м2
Н/м2
Постоянная прогонная нагрузка
qнпост = 953,76 ∙ 3 = 2861,28 Н/м
qпост = 1049,135 ∙ 3 = 3147,41 Н/м
Временные нагрузки
Снеговая нагрузка
Погонная нормативная снеговая нагрузка
qnсн= 3200∙3∙0,7∙0,75 = 5040 Н/м
Погонная расчетная снеговая нагрузка
Sp = Sg ∙м = 3200∙ 0,75∙3 = 7200 Н/м
Ветровая нагрузка
w0= 0,3 кН/м2 (2-й ветровой район)
w=w0∙ гf ∙ Ce ∙ k
гf = 1,4; Ceнав = 0,34; Ceподв = -0,4
i - участок с однозначной эпюрой давления
hi – высота участка с однозначной эпюрой давления
kсрi – усредненный коэффициент изменения ветрового давления по высоте
| участок | высота | tg i | Ki |
|
i=1 i=2 i=3 |
5 10 20 |
0 0,03 0,02 |
0,5 0,65 0,85 |
kicpj = khj + ![]() ∙ tg i ;
∙ tg i ;
kcp1= k5 + ![]() ∙ tg1 = 0,5
∙ tg1 = 0,5
kcp2= k10 + ![]() ∙ tg2 = 0,65 +
∙ tg2 = 0,65 + ![]() 0,03 = 0,8
0,03 = 0,8
kcp3= k20 + ![]() ∙ tg3 = 0,85 +
∙ tg3 = 0,85 + ![]() 0,02 = 1,05
0,02 = 1,05
Расчетные значения ветровой нагрузки
w1нав = w0 ∙ гf ∙ Cенав ∙ kср1 = 0,3∙1,4∙0,34∙0,5=0,0714 кН/м2
w2нав = w0 ∙ гf ∙ Cенав ∙ kср2 = 0,3∙1,4∙0,34∙0,8=0,1142 кН/м2
w3нав = w0 ∙ гf ∙ Cенав ∙ kср3 = 0,3∙1,4∙0,34∙1,05=0,1499 кН/м2
w1подв = w0 ∙ гf ∙ Cеподв ∙ kср1 = 0,3∙1,4∙0,4∙0,5=0,084 кН/м2
w2подв = w0 ∙ гf ∙ Cеподв ∙ kср2 = 0,3∙1,4∙0,4∙0,8=0,134 кН/м2
w3подв = w0 ∙ гf ∙ Cеподв ∙ kср3 = 0,3∙1,4∙0,4∙1,05=0,176 кН/м2
Погонная расчетная ветровая нагрузка
w1нав = w1нав ∙ b = 0,105 ∙ 3=0,315 кН/м
w2нав = w2нав ∙ b = 0,168 ∙ 3=0,504 кН/м
w3нав = w3нав ∙ b = 0,22 ∙ 3=0,66 кН/м
w1подв = w1подв ∙ b = 0,84 ∙ 3=0,252 кН/м
w2подв = w2подв ∙ b = 0,134 ∙ 3=0,402 кН/м
w3подв = w3подв ∙ b = 0,176 ∙ 3=0,528 кН/м
3.2 Конструктивный расчет арки
Расчетное сочетание нагрузок
1-е сочетание: постоянная нагрузка + снеговая + Р↓
414,619 + 788,534 + 37,504 = 1240,66 кН/м
2-е сочетание: постоянная + снеговая + ветровая + Р↓
414,619 + (788,534 + 37,504 + 71,149) ∙ 0,9 = 1222,09 кН/м
Расчетные усилия: М= 1240,657 кНм
N= 328,866 кНм
Определяем предварительные размеры поперечного сечения арки:
Принимаем: h= 171,5см (49 слоев из досок у = 219мм, до острожки 225мм, фрезер пластей с 2-х сторон 5мм)
b= 33,85см (2 слоя из досок у = 219мм, до острожки 225мм, фрезер пластей с 2-х сторон 6 мм, из досок у = 119,5мм, до острожки 125мм, фрезер пластей с 2-х сторон 5,5мм)
Сечение 171,5 х 33,85 см
171,5 х 32,85 см (фрезер с 2-х сторон 10мм)
Расчет арки на прочность
Данный расчет выполняем в соответствии с указаниями СНиП II-25-80* п.4.17
![]() Мд
Мд
– изгибающий момент от действия поперечных и продольных нагрузок, определяемый из расчета по деформационной схеме.
Определение гибкости
л = ![]()
l0 = 0,5 ∙ 64,9 = 32,45 м
S = 64,9м = длинна арки
r = радиус инерции сечения элемента с максимальными размерами брутто
r = 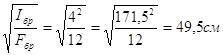
л = ![]() = 65,56 при л = 65,56 < 70→
= 65,56 при л = 65,56 < 70→
ц = 1- a ![]()
Коэффициент a = 0,8 для древесины
Ru = 15∙1∙1∙1,01∙0,8 = 12,12 МПа
Nk = 250,198 кН
о = 1- ![]()
Мд = ![]() 1312,86 кНм
1312,86 кНм
![]() 0,874 < Rc = 1,212
0,874 < Rc = 1,212
При данном значении прочность конструкции обеспечена
3.3 Расчет на устойчивость плоской формы деформирования
Для сжато - изгибаемых элементов при отрицательном изгибающем моменте:
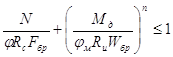
где:
Fбр - площадь брутто с максимальными размерами сечения на участке lр
Wбр – Максимальный момент сопротивления брутто на участке l1
n2 – для элементов без закрепления растянутой зоны из плоскости деформирования и n=1 для элементов, имеющих такие закрепления
ц – Коэффициент продольного изгиба, определяется по формуле (8)
для гибкости участка элемента расчетной длинной lp из плоскости деформирования
цм – коэффициент определяемый по формуле (23)
цм = 140 ![]()
где:
lр – расстояние между опорными сечениями элемента, а при закреплении сжатой кромки в промежуточных точках от смещения из плоскости изгиба расстояние между этими точками.
b – ширина поперечного сечения.
h – максимальная высота поперечного сечения на участке lp
kф – коэффициент зависящий от формы эпюры изгибающих моментов на участке lp
kф = 1,13
Принимаем lp = 2м
цм = 140 ∙ ![]()
r = 0,289∙b = 0,289∙32,85 = 9,49 см
л = ![]() =
=![]() = 21,08 < лпред = 120
= 21,08 < лпред = 120
ц = ![]() = 6,75
= 6,75
о = коэффициент изменяющейся от 1 до 0, учитывающий дополнительный момент от продольной силы, вследствие прогиба элемента, определяемый по формуле:
о = 1- ![]() =1-
=1- ![]() = 0,993
= 0,993
Мд = ![]() =
= ![]() = 1249,403 кНм
= 1249,403 кНм
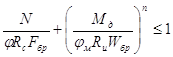
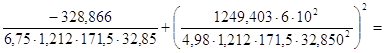 0,443 ≤1
0,443 ≤1
Данное условие выполнено
3.4 Расчет узлов арки
3.4.1 Опорный узел
Расчетные усилия N = -393,06 кН
Q= 150,44 кН
Пролет арки 54м > 18м → конструктивно узел решается в виде плиточного шарнира.
Принимаем hш = 10 см
Из условия размещения болтов назначаем размеры:
S1 =6 ∙ d = 6 ∙ 30 = 180 мм
S2 =3 ∙ d = 3 ∙ 30 = 90 мм
S3 =2,5 ∙ d = 2,5 ∙ 30 = 75 мм (80мм)
d = 30мм – диаметр болта
Толщину башмака принимаем конструктивно 20мм. Проверяем условие, чтобы равнодействующая усилий в наиболее нагруженном болте от действия расчетной поперечной силы Q и момента в башмаке Мб не превышала его минимальной несущей способности.
Rб = 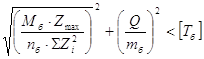
Rб – равнодействующие усилие в максимально нагруженном болте
[Т6] - минимальная несущая способность одного среза болта
Мб - расчетный момент в башмаке M6=Q∙ e
е - расстояние от оси шарнира до центра болтового соединения
nб - число болтов в крайнем ряду, ║ оси элемента
mб - общее число болтов в башмаке
Zi - расстояние между осями болтов в направлении ┴ оси элемента
Zmax - максимальное расстояние между осями болтов в том же направлении
У Zi - сумма квадратов расстояний между рядами болтов
e = 180 ∙ 0,5 +180 + 20 + 50 = 340 мм
Мб = 150,44 ∙ 0,34 = 51,15кНм = 5115 кН см
У Zi = 92 +272+452 = 2835 см2
Rб = 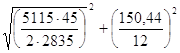 = 42,49 кН <
= 42,49 кН < ![]() ∙ nш = 45 кН
∙ nш = 45 кН
![]() = 2,5∙ d2 = 2,5 ∙ 32
= 22,5 кН
= 2,5∙ d2 = 2,5 ∙ 32
= 22,5 кН
Проверка опорного узла на смятие под углом к волокнам
усм = ![]() < Rсмб ∙ kN
< Rсмб ∙ kN
Rсмб - расчетное сопротивление смятию древесины под углом к волокнам
kN - коэффициент, учитывающий концентрацию напряжений под кромками башмаков
Fсм = 54 ∙ 61 = 3294 см2
Rсмб = 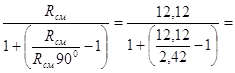 7,19 МПа
7,19 МПа
![]() 0,12 кН/см2 < 0,719 ∙
0,35 = 0,25 кН/см2
0,12 кН/см2 < 0,719 ∙
0,35 = 0,25 кН/см2
Проверка на скалывание по клеевому шву в опорном узле
ф = ![]()
Sx = ![]() =
= ![]() 25116,75 см3
25116,75 см3
Ix = ![]() =
= ![]() 1021414,5 см4
1021414,5 см4
ф = ![]() 0,069 кН/см2 < Rск = 0,14
кН/см2
0,069 кН/см2 < Rск = 0,14
кН/см2
Прочность на скалывании обеспечена.
3.4.2 Коньковый узел
Расчетные усилия: N= -250,198 кН
Q= 166,799 кН
Н = N cos б + Q ∙ sin б = -250.198 0,832 + 166.799 ∙ 0,555 = - 115,59 кН
Н - горизонтальная составляющая усилий
R = Q cos б - N ∙ sin б = 166,799 ∙ 0,832 + 250,198 ∙ 0,555 = 277,63 кН
R - вертикальная составляющая усилий
Коньковый узел конструктивно решается как опорный. Диаметр болтов назначаю такой же, т.е. d =30 мм. Толщина пластины башмака 20 мм.
е = 340мм
Mб = R ∙ е = 277,63 ∙ 0,34 = 94,39 кН м = 9439 кН см
У Zi2 = 92 + 272 + 452 = 2835 см2
Rб = 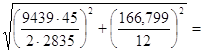 37,96 кН < [Тб] ∙ nш =
38,82 кН
37,96 кН < [Тб] ∙ nш =
38,82 кН
[Тб] = 2,5 ∙ d 2 ∙ ![]() = 2,5 ∙ 32 ∙
= 2,5 ∙ 32 ∙ ![]() = 19,48 кН
= 19,48 кН
Kб – коэффициент используемый при передаче усилий от панелей под углом к волокнам.
Проверка конькового узла на смятие под углом к волокнам
усм = ![]()
Rсмб – расчетное сопротивление смятию древесины под углом к волокнам
kN – коэффициент учитывающий концентрацию напряжений под кромками башмаков.
Fсм = 54 ∙ 81= 4374 см2
Rсмб = 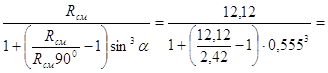 7,19 МПа
7,19 МПа
![]() 0,026 кН/см2 < 0,719 ∙
0,35 = 0,25 кН/см2
0,026 кН/см2 < 0,719 ∙
0,35 = 0,25 кН/см2
Проверка конькового узла на скалывание по клеевому шву:
ф = ![]() 0,044 кН /см2 < Rскб = 0,14
кН/см2
0,044 кН /см2 < Rскб = 0,14
кН/см2
Rскб = 0,14 кН/см2 – расчетное сопротивление древесины скалыванию под углом к волокнам:
Rскб = 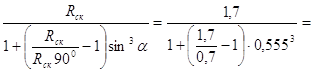 1,4 МПа = 0,14 кН/см2
1,4 МПа = 0,14 кН/см2
4. Обеспечение пространственной устойчивости сооружения
В сооружении плоскостные несущие конструкции при помощи связей в продольном направлении объединяются в общую систему, которая доводиться до неподвижных частей, эта система обеспечивает пространственную неизменяемость, устойчивость, прочность и жесткость конструкции от воздействий внешних сил любого направления при расчетном сочетании нагрузок.
По конструктивному признаку связь - скатная с крестовой решеткой.
Блоки связей спаренные, так как пролет более 18 метров (54м), расположены в торцовых секциях и через 24 метра. Всего 4 блока связей с каждой стороны, что обеспечивает пространственную неизменяемость, устойчивость, прочность и жесткость конструкции.