Реферат: Зонная модель твердого тела. Уравнение Шредингера для кристалла
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Кафедра ЭТТ
РЕФЕРАТ:
«Зонная модель твердого тела. Уравнение Шредингера для кристалла»
МИНСК, 2008
Любое твердое тело представляет собой систему, состоящую из огромного числа ядер и ещё большего числа электронов. Современное состояние математической физики позволяет утверждать, что целый ряд сведений о свойствах такой системы, в том числе и об энергетическом спектре можно получить из решения уравнения Шредингера, описывающего стационарные состояния этой системы. В этом случае уравнение Шредингера имеет вид:
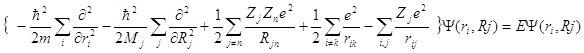
Где m и M соответственно массы электронов и ядер; ri и Rj – радиус-векторы i-го электрона и j-го ядра; Zj и Zn – атомные номера ядер; Rjn , rik, rij – расстояния между соответствующими ядрами и электронами; Е – полная энергия кристалла; Ψ – собственная волновая функция системы электронов и атомов.
В приведенном уравнении первое слагаемое описывает кинетическую энергию электронов, второе – кинетическую энергию ядер. Множители при волновой функции в следующих трёх слагаемых описывают соответственно, потенциальную энергию взаимодействия ядер с друг другом, электронов друг с другом и энергию взаимодействия электронов с ядрами.
Сегодня неизвестны способы точного решения уравнения Шредингера, так как для кристалла волновая функция Ψ зависит от огромного числа (1024-1025) независимых переменных ( в 1см2 содержится примерно 5∙1022 ядер атомов, каждое ядро содержит большое количество электронов).
Теория должна найти разумные допущения, которые позволят решать данное уравнение, сохранить его принципиальные черты, отличающие кристалл от отдельного изолированного атома.
Прежде чем рассматривать свойства твердых тел необходимо рассмотреть закономерности образования твердого тела из отдельных изолированных атомов.
Обобществление электронов в кристалле.
Для того чтобы понять особенности явлений, имеющих место в твердых телах, рассмотрим следующий идеализированный пример. Возьмем атом натрия.
Расположим N атомов натрия на больших расстояниях друг от друга в трехмерном пространстве так, чтобы они образовали в значительно увеличенном виде кристаллическую решетку натрия. Так как расстояния между атомами r значительно больше параметра решетки а( а= 4.3Å; r>>а), то взаимодействием между атомами можно пренебречь.
На рисунке каждый атом изображен в виде потенциальной ямы, внутри которой проведены энергетические уровни 1s, 2s и 2p - укомплектованы у натрия полностью, уровень 3s – наполовину, остальные уровни, расположенные выше уровня 3s – свободны.
Изолированные атомы отделены друг от друга потенциальными барьерами шириной r. Высота барьера для электронов, находящихся на разных уровнях различна. Она равна расстоянию от этих уровней до нулевого уровня 00. Потенциальный барьер препятствует свободному переходу электронов от одного атома к другому.
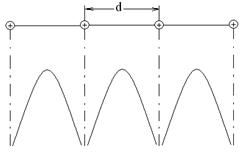
Рис. Ррасположение атомов натрия в линейной цепочке. d-параметр решетки.
Качественная картина распределения плотности вероятности обнаружения электронов на данном расстоянии от ядра показывает, что максимумы этих кривых примерно соответствуют положению боровских орбит для эти электронов.
Теперь начнем сближать атомы натрия таким образом, чтобы в конце однородного сжатия они находились бы на расстояниях, равных параметру решетки. По мере сближения атомов взаимодействие между ними возрастало и достигло максимальной величины при образовании кристалла. При образовании кристалла потенциальные кривые, отделяющие соседние атомы, частично перекрываются и дают результирующую потенциальную кривую (1α2), проходящую ниже нулевого уровня 00. При сближении атомов уменьшается не только ширина барьера, но и его высота. При этом оказывается, что высота барьера между атомами в кристалле оказывается даже ниже первоначального положения уровня валентных электронов 3s. Таким образом, валентные электроны получают возможность практически беспрепятственно переходить от одного атома к другому.
Об этом свидетельствует и характер волновых функций этих электронов: они перекрываются настолько сильно, что дают электронное облако практически равномерной плотности, чему соответствует состояние полного обобществления валентных электронов, при котором вероятность обнаружения их в любом месте решетки совершенно одинакова.
Электронные облака внутренних оболочек атома не перекрываются вследствие чего состояние внутренних электронов в кристалле остаётся фактически таким же, как и в изолированных атомах.
Коллективизация валентных электронов является прямым следствием физической эквивалентности всех ионов решётки и поэтому каждый электрон принадлежит одновременно всем ионам решётки с равной вероятностью может быть обнаружен вблизи любого из них. Такие электроны образуют в кристалле электронный газ.
Основные приближения зонной теории.
1. Зонная теория твёрдых тел является моделью изучения электронных свойств идеальных периодических структур кристаллов. В этом суть первого приближения.
Ранее приведённое уравнение Шредингера удобно представить в виде:
![]()
где
![]() - гамильтониан кристалла;
- гамильтониан кристалла;
![]() - собственная волновая функция гамильтониана;
- собственная волновая функция гамильтониана;
Е – энергия кристалла.
Оператор Гамильтона
включает в себя: оператор кинетической энергии электронов - ![]() ; оператор кинетической энергии ядер -
; оператор кинетической энергии ядер - ![]() ; потенциальную энергию попарного
взаимодействия электронов
; потенциальную энергию попарного
взаимодействия электронов ![]() ,
ядер
,
ядер ![]() , электронов с ядрами
-
, электронов с ядрами
- ![]() . В этих обозначениях
уравнение имеет вид:
. В этих обозначениях
уравнение имеет вид:
![]()
2. Второе упрощение называют упрощением Борна-Оппенгеймера, при котором всю систему частиц разделяют на электроны и атомные ядра и рассматривают их кинетические энергии в равновесном состоянии. Пользуясь законом равенства количества движения в системе ядро-электрон без учёта количества движения от внешнего источника можем записать:
![]()
Для водорода M=1840m. Из-за разницы масс будет и разница в скоростях теплового движения ядер и электронов. Ядра можно считать неподвижными по сравнению с электронами. Таким образом, движение электронов и ядер можно считать независимым, проходящим без обмена энергией между электронной и ядерной подсистемами частиц. В этом и состоит смысл адиобатического приближения (А.И. Ансельм “Введение в теорию полупроводников”, Физмат. изд. 1963 – в этой книге можно найти много интересного о методах решения уравнения Шредингера для кристалла).
3. Третье допущение называют одноэлектронным приближением. Рассмотрим его более подробно в следующем параграфе.
Таким образом, в основе зонной теории, приводящей к зонной картине электронного энергетического спектра твёрдого тела, лежат следующие главные приближения:
1. Твёрдое тело представляет собой идеально переодический кристалл.
2. Равновесные положения узлов кристаллической решётки фиксированы, т.е. ядра атомов считаются неподвижными (адиабатическое приближение). Малые колебания атомов вокруг равновесных положений, которые могут быть описаны как фононы, вводятся в последствии как возмущения электронного энергетического спектра.
3. Многоэлектронная задача сводится к одноэлектронной: воздействие на данный электрон всех остальных описывается некоторым усреднённым переодическим полем.
4. Одноэлектронное описание многоэлектронных систем.
5. Идея одноэлектронного приближения ведёт своё начало с доквантово-механической – боровской – теории сложных атомов. Эта модель основана на допущении, что действие на данный электрон всех ядер и всех остальных электронов системы приближённо можно заменить действием некоторого усреднённого “эффективного” поля, потенциальная энергия электрона в котором – так называемый “эффективный одноэлектронный потенциал”
![]() (1)
(1)
зависит только от координат этого электрона (x,y,z). Таким путём исследование различных многоэлектронных систем сводится к исследованию движения одного электрона в полях с различными потенциалами.
В дальнейшем нас будут интересовать не любые состояния электрона в поле (1), а лишь так называемые стационарные состояния. Таким состояниям в боровской модели атома соответствовали устойчивые орбиты электронов. В квантовой механике боровские орбиты для стационарных состояний электрона заменяются определёнными во всём трёхмерном пространстве одноэлектронными волновыми функциями,
![]() (2)
(2)
которые называют также орбиталями.
Стационарным состояниям соответствуют определённые энергетические уровни. Таким образом последовательности одноэлектронных орбиталей для стационарных состояний электрона в поле (1)
![]() …
(3)
…
(3)
отвечает последовательность одноэлектронных уровней
![]() … (4)
… (4)
или одноэлектронный энергетический спектр системы. Может случиться, что нескольким функциям (3) соответствует один и тот же энергетический уровень. Такой уровень называется вырожденным, а число разных функций, соответствующих этому уровню называют кратностью вырождения уровня.
Ψ1 --> E1 E1 - вырожденный уровень
Ψ2 --> E1 2 кратность вырождения
Вышесказанного вполне достаточно, чтобы понять чем занимаются почти все специалисты по электронной структуре кристаллов. Они вычисляются для разных систем орбитами (3) и уровни (4), поскольку в в одноэлектронном приближении наборы (3) и (4) исчерпывают все, что можно сказать об электронном строении и электронных свойствах любой системы.
Действительно, система из N электронов описывается в одноэлектронной модели просто как совокупность частиц, каждая из которых находится на определенной орбитали (3). При этом стремление к минимальной энергии заставляет электроны занимать возможно более низкие уровни, однако в силу принципа Паули на каждой орбитали должно находиться не более двух электронов (в этом случае они имеют противоположные спины). Тогда оптические свойства системы определяются одноэлектронными переходами из одного состояния ( Ψί) в другое (Ψj), а энергия , необходимая для отрыва электрона с некоторой орбитали Ψj – так называемый «орбитальный потенциал ионизации», - будет равна энергии соответствующего одноэлектронного уровня
Eί, взятый с обратным знаком. В то время как схема уровней (4) дает информацию об оптических свойствах, а также об электропроводности кристаллов, вид орбиталей позволяет судить о распределении электронной плотности в системе.
Это обстоятельство связанно с физическим смыслом волновой функции. Квадрат модуля волновой функции в некоторой точке пространства пропорционален вероятности нахождения электрона в этой точке пространства. Если взять, как это делают обычно, орбитали (3) нормированными т.е. :
|Ψ|2dV=1
где интеграл взят по всему пространству, то величина |Ψ|2 для каждой из орбиталей даст распределение вероятностей для электрона на соответствующей орбитали.
Результирующая электронная плотность для всей системы определяется выражением
ρ(r)= 2Σ'|Ψί|2 +Σ''|Ψj|2
где Σ' – означает суммирование по дважды занятым орбиталям, а Σ'' – суммирование по однократно занятым орбиталям.
Способы решения одноэлектронных задач связанны с именами Хартри и Фока. Особенно много в этом направлении сделал ленинградский ученый Владимир Александрович Фок. Метод Хартри-Фока позволяет много-электронную задачу свести к одноэлектронной, путем замены взаимодействия каждого электрона с усредненным полем всех остальных электронов. Обозначив потенциальную энергию i-го электрона в усредненном поле (Ωί), и зависимую не только от движения всех электронов, но и от движения данного электрона, мы переходим к усредненному полю. Усредненное поле не только определяет движение электрона, но и само зависит от его движения. Его вызывают самосогласованным. С помощью самосогласованного поля удалось значительно продвинуться в решении уравнения Шредингера.
Приближение сильно и слабо связанных электронов
Несмотря на значительное упрощение, которое достигается одноэлектронным приближением, точное решение уравнения Шредингера оказывается очень сложным. Поэтому для его решения были разработаны различные приближения, в частности приближения, в частности приближения сильно и слабо связанных электронов.
Физический смысл этих приближений заключается в следующем: из рис.1 видно, что в кристалле имеются области, где потенциал решетки меняется очень резко, и области, где он меняется слабо. Первый из них располагается непосредственно вблизи ядер. Электрическое поле в этих областях практически такое же как и в изолированных атомах. Области, где потенциал меняется слабо, располагаются между ядрами. На их долю приходится основная доля объема кристалла.
В соответствии с этим при выборе потенциальной энергии U(r) весь объем кристалла удобно делить на две части:
1. Области со слабым полем, в которых
U(r)=U0(r)+δU(r), δU(r)<<U0(r) (10)
где U0(r)=const представляет собою потенциальную энергию электрона в поле положительных ионов в предположении, что это поле компенсировано полем всех остальных электронов, кроме данного; δU(r) учитывает неполную локальную компенсацию поля ионов электронами. Она имеет периодический характер с периодом, равным
На области с сильным полем в которых:
U(r)=Ua+δU(r) δU(r)<<Ua (11)
где Ua - потенциальная энергия электрона в изолированном атоме.
Она является периодической функцией с периодом равным постоянной решетки; δU(2) поправочный член, учитывающий влияние на эту энергию соседних узлов решетки. Волновые функции электронов, обладающих различной энергией, имеют различный характер локализации в объеме кристалла. Волновые функции внутренних электронов на незначительном расстоянии от ядер обращаются практически в ноль и для них пригодна формула (I I). Это будет приближение сильной связи. Для внешних валентных электронов лучше подходит приближение слабо связанных электронов в котором используется формула (I0).
Превращение энергетических уровней свободных атомов в энергетические зоны при образовании кристалла.
Взаимодействие атомов при образовании твердого тела приводит к расширению энергетических уровней атомов и превращению их в кристалле в энергетические зоны.
В атомах время жизни электрона в возбужденном состоянии τ = 10-8c
Вспомним принцип неопределенности для энергии
∆E ∆t ≥ ħ
∆t ≈ τ
тогда
∆E ≈ ħ / τ ≈ 10-7 эВ (ħ = 10-15 эВс)
Такова естественная ширина спектральных линий, испускаемых атомами.
В кристалле все электроны благодаря туннельному эффекту имеют возможность переходить от атома к атому. В результате уменьшается степень локализации электронов на определенных атомах, что изменяет значение неопределенностей их энергий, т.е. приводит к размытию уровней энергии и превращению их а полосы или зоны.
Так как глубина потенциального поля не играет принципиальной роли, можно заменить потенциальный рельеф кристалла рельефом с конечной глубиной. Кроме этого непрямоугольные барьеры в модели кристалла удобно заменить прямоугольными. Такую модель потенциального рельефа называют моделью Кронинга-Пенни.
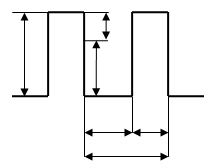
Мы уже знаем как определяется прозрачность такого барьера:
D = D0 e-4π/h ![]()
![]()
Если ширина потенциальной ямы равна α, а скорость движения электрона равна υ, то за 1 секунду электрон подойдет к барьеру υ/α раз.
ν = υ/α D - дает частоту перехода электрона в соседний атом
ν = υ/α D0 e-4π/h ![]()
![]()
Величина τ обратная ν выражает среднее время пребывания электрона у определенного атома
τ = 1/ ν ≈ 1/ υ/α D0 e-4π/h ![]()
![]()
так как α ≈ 10-8 см; υ ≈ 108 см/с; D0 ≈ 1; υ/α ≈ 1016с-1
Для изолированных атомов d ≥ 30Å (среднее расстояние между молекулами газа при нормальных условиях). U-E – энергия ионизации атома. Для Na
U-E = 10 эВ. Найдем τ в этом случае:
τ ≈ 1020лет; ν ≈ 10-27с-1
В кристалле b ≈ 1Å, тогда ν ≈ 1015с-1 ; τ ≈ 10-20 с
При такой частоте перехода валентных электронов от атома к атому теряет, очевидно, смысл говорить о принадлежности их определенным атомам.
Таким образом туннельный эффект в кристалле доводит среднее время жизни валентного электрона в определенном узле решетки до τ ≈ 10-15с. В соответствии с принципом неопределенности, неопределенность в значении энергии таких электронов равна:
∆E ≈ 10-12эрг ≈ 1эВ
Это означает, что энергетический уровень валентных электронов, имеющий в изолированном атоме ширину 10-7эВ превращается в кристалле в энергетическую зону шириной порядка единиц электроновольт.
Для электронов внутренних оболочек натрия картина изменяется. Например, для электронов 1s (U-E ≈ 1000 эВ, d ≈ 3Å в результате ν ≈ 10-27 с-1; τ ≈ 1020лет) энергетические уровни этих атомов в кристалле такие же узкие, как и в отдельном атоме. По мере перехода к валентным электронам высота и ширина потенциального барьера уменьшается, вероятность туннельного перехода электронов увеличивается, вследствие чего растет ширина энергетических зон.
На рисунке снизу приведены урони изолированного атома натрия, слева – образование
Зон, обусловленное расширением уровней при уменьшении расстояния между атомами. Электрические свойства твердых тел в основном определяют особенностями образования энергетических зон при сближении атомов и образовании кристалла.
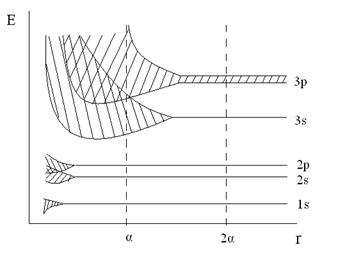
Рис. Расширение энергетических уровней при сближении атомов Na.
ЛИТЕРАТУРА
1. Мирошников М.М. Теоретические основы оптико-электронных приборов: учебное пособие для приборостроительных вузов. -- 2-е издание, перераб. и доп.—Спб.: Машиностроение,2003 -- 696 с.
2. Порфирьев Л.Ф. Теория оптико-электронных приборов и систем: учебное пособие.— Спб.: Машиностроение,2003 -- 272 с.
3. Кноль М., Эйхмейер И. Техническая электроника, т. 1. Физические основы электроники. Вакуумная техника.—М.: Энергия, 2001.