Лабораторная работа: Дослідження електричного кола змінного струму з паралельним з’єднанням віток
Раздел: Рефераты по физике
Тип: лабораторная работа
Робота 7. Дослідження електричного кола змінного струму з паралельним з’єднанням віток
7.1 Мета роботи
Дослідити режим роботи електричного кола з паралельним з’єднанням котушки індуктивності і ємності при різних частотах, вивчити вплив С і L на явище резонансу струмів та його використання для регулювання коефіцієнта потужності.
7.2 Короткі теоретичні відомості
На відміну від кола з послідовним з’єднанням, в якому через всі елементи протікає однаковий струм, в колах з паралельним з’єднанням віток однаковою буде напруга, яка прикладається до паралельних віток. Тому метою досліджень будуть струми, які протікають у вітках.
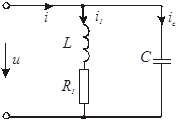
Рис. 7.1.
На
прикладі кола, яке складається із паралельно включених індуктивної котушки з
індуктивністю L і активним опором R1 та ємності С, можна встановити на підставі
векторної діаграми зв’язки між напругою живлення U і струмами і, і1, іС
(рис. 7.1). До кожної вітки цього кола прикладена напруга U. Тому побудову
векторної діаграми починають з вектора напруги ![]() . Довжина вектора струму
. Довжина вектора струму ![]() буде дорівнювати
буде дорівнювати
![]() /7.1/
/7.1/
бо R1 і xL= ωL з’єднані
послідовно. Відкладають цей вектор відносно вектора ![]() під кутом
під кутом
![]() /7.2/
/7.2/
Побудований
таким чином вектор ![]() розкладають
на дві складові: активну складову Ia =I1cosφ1 і реактивну IL=I1sinφ1, як показано на рис.7.2.
розкладають
на дві складові: активну складову Ia =I1cosφ1 і реактивну IL=I1sinφ1, як показано на рис.7.2.

Модуль
вектора струму ![]() знаходять за
формулою
знаходять за
формулою
![]() /7.3/
/7.3/
Вектор
струму ![]() буде випереджати
вектор напруги
буде випереджати
вектор напруги ![]() на кут
на кут ![]() .
.
Струм в нерозгалуженій частині кола буде дорівнювати геометричній сумі струмів у вітках, тобто
![]()
Довжина цього вектора
![]() /7.4/
/7.4/
а кут
між векторами ![]() і
і ![]() знаходять із векторної діаграми
або за формулою
знаходять із векторної діаграми
або за формулою
![]() /7.5/
/7.5/
Для дослідження впливу параметрів R, L і C на струми у вітках необхідно в рівнянні /7.4/ струми виразити через напругу і опори.
Активна складова струму першої вітки
![]() /7.6/
/7.6/
де ![]()
![]() – активна провідність першої вітки,
– активна провідність першої вітки, ![]() згідно векторної діаграми, наведеної на
рис. 6.3, б.
згідно векторної діаграми, наведеної на
рис. 6.3, б.
Реактивна складова струму першої вітки
![]() /7.7/
/7.7/
де ![]() – реактивна індуктивна
провідність першої вітки.
– реактивна індуктивна
провідність першої вітки.
Струм у другій вітці
![]() , /7.8/
, /7.8/
де bC – реактивна ємнісна провідність другої вітки.
Підставивши в /7.4/ замість струмів у вітках вирази згідно формул /7.6/, /7.7/ і /7.8/, одержимо
![]() /7.9/
/7.9/
де Y – повна провідність кола.
Узагальнюючи викладену методику на коло з паралельним з’єднанням n віток, можна записати, що активна провідність кола
![]() ; /7.10/
; /7.10/
реактивна індуктивна провідність кола
![]()
![]() /7.11/
/7.11/
і реактивна ємнісна провідність кола
![]() /7.12/
/7.12/
де і – номер вітки кола (і=1, 2, …, n).
Повна провідність кола
![]() / 7.13/
/ 7.13/
Отже, за аналогією з /7.9/ закон Ома для кола з паралельним з’єднанням n елементів або віток має вид
I=YU. /7.14/
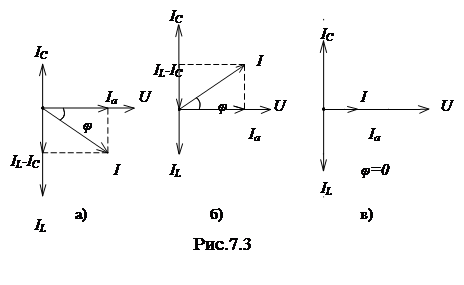 |
На підставі рівняння /7.13/ можна зробити висновок, що характер струму в колі з паралельним з’єднанням віток залежить не тільки від величини опорів, але і від співвідношення між провідностями bL і bC.
При bL > bC струм IL > IC і повна провідність буде мати активно-індуктивний характер. Струм в нерозгалуженій частині кола, наведеного на рис. 7.1, буде відставати за фазою від напруги, як показано на векторній діаграмі (рис. 7.3, а).
При bL < bC струм IL < IC і повна провідність кола буде активно-ємнісною. Струм в нерозгалуженій частині буде випереджати за фазою напругу, як показано на векторній діаграмі (рис. 7.3, б).
При bL = bC струм IL = IC, провідність кола стає рівною активній провідності (Y=g). Струм в нерозгалуженій частині кола співпадає за фазою з напругою і визначається лише активною провідністю. Це явище називається резонансом струмів. Воно зумовлене обміном енергією магнітного поля котушки індуктивності з енергією електричного поля конденсатора. Цей обмін відбувається з частотою 2ω і не зв’язаний з джерелом напруги. При резонансі струми IL і IC можуть значно перевищувати струм в нерозгалуженій частині кола, як показано на векторній діаграмі (рис. 7.3, в), і тому резонанс в колі з паралельним з’єднанням називають резонансом струмів.
Для електричних кіл з n паралельними вітками умовою резонансу струмів є умова
![]() /7.15/
/7.15/
Для кола, наведеного на рис. 7.1, умовою резонансу є
![]() або
або ![]() /7.16/
/7.16/
Із рівняння /7.16/ слідує, що резонансу в колі можна досягнути зміною частоти ω, індуктивності котушки L або ємності С.
Якщо L і С сталі величини, то частота, при якій виникає явище резонансу, називається резонансною частотою і позначається ω0. Згідно з /7.16/ резонансна частота
![]() /7.17/
/7.17/
На
відміну від кола з послідовним з’єднанням R, L і С елементів, в
якому власна частота коливань ![]() в
колі з паралельним з’єднанням ω0 залежить не тільки від L і С, а також від
активного опору R. Із /7.17/ слідує, що
в
колі з паралельним з’єднанням ω0 залежить не тільки від L і С, а також від
активного опору R. Із /7.17/ слідує, що ![]() > ω0 і тільки за умови R1=0
> ω0 і тільки за умови R1=0 ![]() =ω0 .
=ω0 .
При незмінних ω і L часто добиваються резонансу зміною С, і це буде за умови
![]() /7.18/
/7.18/
Рівняння
/7.18/ показує, що активний опір R1 призводить до зменшення С0 у порівнянні з
випадком, коли R1 = 0 (![]() ).
).
Часто
в радіотехніці добиваються виникнення резонансу зміною індуктивності котушки L при сталих
значеннях ![]() і С. У цьому
випадку згідно рівняння /7.16/ резонанс наступить при
і С. У цьому
випадку згідно рівняння /7.16/ резонанс наступить при
![]() . /7.19/
. /7.19/
Слід відмітити, що при резонансі стосовно до джерела напруги коло веде себе так, ніби реактивних провідностей bL і bC немає.
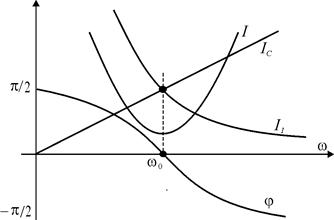
Рис. 7.4
Це зумовлене тим, що реактивні струми IL і IC знаходяться у протифазі (зсунуті в часі на кут π), тобто сума миттєвих значень цих струмів дорівнює нулю.
На рис. 7.4 наведені залежності I, I1, IC і φ=f(ω), із яких видно, що струм в нерозгалуженій частині кола змінюється за параболічним законом, а струм в конденсаторі – за законом гіперболи.
Потужності, які споживають елементи кола, визначають за такими формулами:
активна
![]() /7.20/
/7.20/
реактивна
![]() /7.21/
/7.21/
і
повна ![]() /7.22/
/7.22/
Електричні кола з паралельним з’єднанням віток знайшли широке застосування в різних галузях електротехніки та електроніки. Це пояснюється тим, що при належній добротності вони характе- ризуються досить ефективними фільтраційними властивостями. В силових електротехнічних установках паралельне під’єднання конденсаторів до вітки з активно-індуктивним опором (асинхронний двигун) підвищує коефіцієнт потужності (cosφ), що призводить до зменшення споживання електроенергії.
7.3 Програма роботи
1. Дослідити резонанс струмів при зміні частоти.
2. Дослідити резонанс струмів при зміні ємності.
3.
При сталих значеннях ![]() і С
визначити експериментально величину індуктивності котушки, при якій виникає
резонанс. Оцінити вплив опору котушки R1 на величину L0.
і С
визначити експериментально величину індуктивності котушки, при якій виникає
резонанс. Оцінити вплив опору котушки R1 на величину L0.
4.
Побудувати векторні діаграми струмів для частот ![]() ,
, ![]() і
і
![]() .
.
5.
Побудувати на одному графіку залежності І, ІL, ІС, Y і ![]() .
.
7.4 Опис лабораторної установки
Лабораторна робота проводиться на лабораторному стенді УИЛС. Для виконання роботи використовують:
- джерело змінної напруги з регульованою частотою;
- блок індуктивностей;
- блок ємностей;
- цифрові вимірювальні прилади для вимірювання напруги, струму і частоти.
Напругу джерела живлення змінюють ручкою “Напряжение”, а її частоту - ручками “Частота” дискретно і плавно.
Дослідження кола виконується за схемою, наведеною на рис.7.5. Вимірювання частоти здійснюють приладом 4372, а напругу і струм -цифровими приладами.
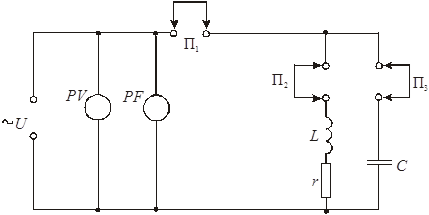
Рис.7.5
7.5 Порядок виконання роботи
1. На набірному полі стенда складають електричне коло, зображене на рис.7.5. Опором R1 буде опір котушки індуктивності. Величини індуктивності (регульованої і нерегульованої) і ємності (регульованої і нерегульованої) задаються викладачем. Напругу живлення виставляють в межах 10...20 В із умови, щоби струми у вітках не перевищували значень, вказаних на котушках і конденсаторах. Виставлену напругу підтримують незмінною під час всіх дослідів. Після на місце перемички П1 під’єднують міліамперметр. Змінюючи частоту ступінчасто та плавно і спостерігаючи за показом міліамперметра, добиваються резонансу, якому буде відповідати мінімальне значення струму І0. Резонансну частоту необхідно виміряти з максимальною точністю. Для цього, плавно регулюючи частоту, декілька разів перейти точку мінімуму частотної характеристики кола. Далі вимірюють струми у вітках і результати вимірювань заносять в четвертий рядок табл.1.
Повторити вимірювання на трьох частотах менших і на трьох більших від резонансної.
2. Залишивши незмінною величину вхідної напруги, виставити її частоту f = 1000 Гц. Змінюючи ступінчасто і плавно ємність блока конденсаторів, добитись резонансу у колі на цій частоті. Записати величину ємності і значення струмів. Повторити вимірювання при трьох значеннях ємності менших и при трьох значеннях більших від резонансної. Результати вимірювань записати в табл.1.
Таблиця 1
|
№ з/п |
Умови дослідів | Вимірювання | Обчислення | ||||||||||||||||||||||
|
U B |
f Гц |
I мА |
I1 мА |
IС мА |
C мкФ |
Y Сім |
ук Сім |
g1 Сім |
bL Сім |
bC Сім |
P Вт |
S ВА |
cos |
||||||||||||
| 1 |
U, C, L = const; f = var |
|
|||||||||||||||||||||||
| 2 |
|
||||||||||||||||||||||||
| 3 |
|
||||||||||||||||||||||||
| 4 |
|
||||||||||||||||||||||||
| 5 |
|
||||||||||||||||||||||||
| 6 |
|
||||||||||||||||||||||||
| 7 |
|
||||||||||||||||||||||||
| 1 |
U, f, L = const; C= var |
|
|||||||||||||||||||||||
| 2 |
|
||||||||||||||||||||||||
| 3 |
|
||||||||||||||||||||||||
| 4 |
|
||||||||||||||||||||||||
| 5 |
|
||||||||||||||||||||||||
| 6 |
|
||||||||||||||||||||||||
| 7 |
|
||||||||||||||||||||||||
3. Не змінюючи напруги і
частоти, виставити ємність ![]() .
Потім необхідно підібрати таку індуктивність L0 із блока
індуктивностей, при якій виникне в колі резонанс струмів. Якщо наявних котушок
індуктивностей недостатньо для режиму резонансу, то треба змінити величину
ємності і пошук повторити.
.
Потім необхідно підібрати таку індуктивність L0 із блока
індуктивностей, при якій виникне в колі резонанс струмів. Якщо наявних котушок
індуктивностей недостатньо для режиму резонансу, то треба змінити величину
ємності і пошук повторити.
При резонансі виміряти
струми І, І1 і ІС, визначити С, сумарний опір котушок ![]() та
та ![]() і занести їх значення до звіту. За формулою /7.19/
при
і занести їх значення до звіту. За формулою /7.19/
при ![]() визначити розрахункове
значення
визначити розрахункове
значення ![]() і порівняти його з
і порівняти його з
![]() .
.
Для оцінки впливу
![]() на величину резонансної
індуктивності
на величину резонансної
індуктивності ![]() потрібно
підставити в /7.19/ R1 = 0 і визначити
потрібно
підставити в /7.19/ R1 = 0 і визначити ![]() . Із порівняння
. Із порівняння ![]() і
і ![]() зробити
висновок.
зробити
висновок.
4. За даними
вимірювань і розрахунків побудувати в одному масштабі діаграми струмів для
частот ![]() ,
, ![]() і
і ![]() .
.
5. За результатами вимірювань необхідно обчислити:
- повну провідність кола (формула 7.9);
- повну провідність котушки
![]() ;
;
- активну провідність котушки (всього кола)
![]() ;
;
- реактивну провідність котушки
![]() ;
;
- реактивну провідність конденсатора (формула 7.8);
- активну потужність (формула 7.20);
- повну потужність (формула 7.22);
- коефіцієнт потужності
![]() .
.
За результатами
вимірювань і обчислень побудувати графіки струмів ![]() ,
, ![]() і
і
![]() , а також повної провідності
, а також повної провідності
![]() і коефіцієнта потужності
і коефіцієнта потужності ![]() в залежності від ємності при
незмінних величинах U, f і L.
в залежності від ємності при
незмінних величинах U, f і L.
7.6 Контрольні запитання
1. Як визначити повну провідність електричного кола з паралельним з’єднанням віток?
2. Як записати закон Ома для електричного кола з паралельним з’єднанням віток?
3. Яка умова резонансу в електричному колі з паралельним з’єднанням віток?
4. Зміною яких параметрів можна викликати резонанс у колі з паралельним з’єднанням віток?
5. Чому резонанс у колі з паралельним з’єднанням віток називають резонанс струмів?
6. Який вид має векторна діаграма струмів з паралельним з’єднанням віток при резонансі?
7. Як впливає на резонансну частоту активний опір котушки індуктивності?
8. Як впливає частота напруги на величину ємності С0?
9. Чи впливає
досягнення резонансу зміною ![]() ,
С і L на величину струму в нерозгалуженій частині кола?
,
С і L на величину струму в нерозгалуженій частині кола?
10. Як можна
підвищити ![]() кола, яке має
індуктивний характер?
кола, яке має
індуктивний характер?