Курсовая работа: Дослідження збіжності рішень для диференціальних рівнянь у частинних похідних, отриманих методом сіток

Міністерство освіти і науки України

Сумський державний університет

Кафедра інформатики

Курсова робота

на тему:

«Дослідження збіжності рішень для диференціальних рівнянь у частинних похідних, отриманих методом сіток»

Суми 2006

Вступ

Актуальність теми. Задачі, що відносяться до диференціальних рівнянь у частинних похідних другого порядку, виникають у різних прикладних областях, зокрема в задачах акустики, електродинаміки, динамічної теорії пружності тощо. Найчастіше при їх розв’язуванні використовують метод скінчених різниць(метод сіток). За цим методом вихідну диференціальну задачу у частинних похідних замінюють відповідною різницевою схемою, що є системою скінченої кількості алгебраїчних рівнянь. Тобто для розв’язування неперервної задачі будують дискретну модель, характер поведінки якої описують різницеві рівняння. Очевидно, будь-яка дискретна модель не тотожна вихідній неперервній задачі.

Особливістю наближених методів є те, що кожному рівнянню можна поставити у відповідність велику кількість різницевих апроксимацій, що мають майже однакові характеристики. Тому побудова різницевих схем, властивості яких якнайповніше відповідають вихідній диференціальній задачі, — суть і предмет методу скінчених різниць, а розвиток теорії різницевих схем природно шукають у покращенні порядку апроксимації, а також у зменшенні кількості арифметичних операцій для знаходження розв’язків. Іншими словами, різницева схема повинна якомога краще моделювати властивості вихідного диференціального рівняння, до того ж кількість арифметичних дій, потрібних для знаходження розв’язку, має бути по можливості пропорційна кількості вузлів сітки.

Побудова різницевих схем для рівнянь у частинних похідних з узагальненими розв’язками, швидкість збіжності яких узгоджена з гладкістю цих розв’язків, привертає сьогодні особливу теоретичну увагу. Як зазначається або приймається за очевидне у кожній роботі з чисельних методів, основним питанням для теорії та практики наближених методів є питання точності розв’язку. Дослідження задач з негладкими розв’язками для рівнянь гіперболічного типу потребують особливої уваги через те, що негладкості середовища для таких рівнянь не зникають з часом. Проблема узагальнюється таким чином: як покращити точність наближеного методу, не збільшуючи при цьому паразитичних осциляцій, які з’являються при переході на кожний наступний ярус. Це явище виникає, коли розв’язок негладкий, має розриви та особливі точки (наявні сконцентровані зовнішні сили, точкові джерела тощо). Причина таких осциляцій — дисперсія різницевої схеми по відношенню до диференціальної задачі, тобто відмінність (відставання або випередження) фазової швидкості сіткових гармонік від гармонік диференціальних. Звідси ясно, якою важливою є побудова таких схем для розв’язування гіперболічних рівнянь, де враховані дисперсійні властивості неперервної моделі і, можливо, до мінімуму зведений спотворюючий вплив цих властивостей.

Стан проблеми. Огляд літератури. Проблема існування дисперсії розглядалася багатьма авторами. Першими роботами, у яких було відмічено зв’язок між дисперсією різницевих схем та втратою точності розв’язків рівнянь гіперболічного типу, були роботи К. Роберта, В. Вайса та Дж. Фромма, в яких дисперсія досліджувалася для різних різницевих схем, що апроксимують гіперболічне рівняння першого порядку. Надалі на існування дисперсії для одновимірних рівнянь вказувалося в роботах С. Орзаґа, Р. Чина. М.М. Москальковим показаний зв’язок осциляцій сіткових розв’язків з дисперсією гармонік різницевої схеми для одновимірних гіперболічних рівнянь як першого, так і другого порядку. Різними авторами проводився дисперсійний аналіз для різних задач математичної фізики. Для рівнянь газової динаміки розв’язувалися проблеми зв’язку дисперсії та стійкості різницевих схем. Для спектральних методів розв’язування задач гідродинаміки подібні проблеми ставилися. Огляд робіт, присвячених цьому питанню, можна знайти в роботі Л. Трефетхена, де досліджувалися дисперсійні властивості різницевих схем, що апроксимують двовимірне хвильове рівняння. За допомогою методу диференціальних наближень проблема дисперсії також досліджувалася.

Пропонувалися різні методи боротьби з наслідками дисперсії —паразитичними осциляціями розв’язків гіперболічних рівнянь. Один з них — введення в рівняння так званої штучної в’язкості (див. роботу П.Роуча). Однак цей спосіб не завжди задовільний: втрачається справжній профіль розв’язку та ускладнюються алгоритми, особливо, коли необхідно працювати з великою кількістю вузлів сітки. За іншими методами, що враховують існування дисперсії, пропонується вводити додатковий антидисперсійний ярус, або розглядати не ортогональні сітки як на площині, так і в тривимірному просторі.

В роботах О.С. Макаренка та М.М. Москалькова було вперше доведено, що в двовимірному випадку, виявляється, існує залежність дисперсії різницевої схеми не лише від номера сіткових гармонік, а й від напрямку руху хвилі. Для неявних різницевих схем для двовимірного гіперболічного рівняння було показано, що можна суттєво покращити дисперсію у заданому напрямку руху хвилі за допомогою вибору вагів схеми.

В роботі В.Л. Макарова, С.В. Макарова, М.М. Москалькова було помічено, що у різницевих схем на правильних трикутних сітках дисперсійні властивості кращі за дисперсійні властивості схем на звичайних шаблонах прямокутної сітки. Пояснюється це тим, що існує залежність між виглядом шаблону та дисперсією схеми. Відмічалося, також, що на правильній трикутній сітці можна побудувати схеми четвертого порядку точності для рівняння Пуассона. Вперше подібне покращення апроксимації для не ортогональних сіток розглядав В.І. Лебедев.

Чисельні методи рішення диференціальних рівнянь у частинних похідних 2-го порядку

Загальний вигляд диференціальних рівнянь у часткових похідних 2-го порядку:

      (1)

Розв’язком рівняння (1) називається функція u=u(x,y), що перетворює це рівняння на тотожність. Графіком розв’язку є поверхня в просторі Oxyu.

Рівняння (1) називається лінійним, якщо воно першого степеня щодо шуканої функції і всіх її похідних і не містить їхніх добутків, тобто це рівняння може бути записане у вигляді

 (2)

У загальному випадку A,B,C,a,b,c - це коефіцієнти, що можуть залежати тільки від х,у. Уводиться визначення дискримінанта:

У залежності від знака дискримінанта D лінійне диференціальне рівняння (2) відноситься до одного з наступних типів:

Якщо D>0, то рівняння еліптичне.

Якщо D=0, то рівняння параболічне.

Якщо D<0, то рівняння гіперболічне.

Якщо D не зберігає знак – рівняння змішаного типу.

Приклади:

 рівняння еліптичного типу.

 - рівняння параболічного типу.

 рівняння гіперболічного типу.

Рівняння вигляду - називається характеристичним рівнянням. Розв’язки цього рівняння називають характеристиками.

Початкові і крайові умови

Диференціальні рівняння в часткових похідних мають незлічену множину розв’язків, тому для однозначності розв’язку необхідно до вихідного рівняння приєднати додаткові умови. Для диференціальних рівнянь у часткових похідних 2-го порядку вони можуть бути початковими і граничними. По суті, розрізнити ці умови можна лише в тому випадку, коли одна з незалежних змінних диференціального рівняння відіграє роль часу, а інша – роль координати. Тоді якщо умови задані для початкового моменту часу, то це початкові умови, а умови, що відносяться до фіксованих значень координат – граничні або крайові.

Представлення часткових похідних у скінчено-різницевому вигляді

Розглянемо диференціальне рівняння ;

Апроксимуємо часткові похідні відповідними різницями:

.

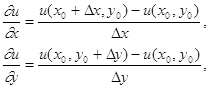
Аналогічно можна записати

тобто різницю зміщаємо до центра

Формула для змішаної похідної

Ці формули переходу до різницевих схем можна записати, використовуючи позначення:

,

,

.

Скористаємося розкладанням у ряд Тейлора:

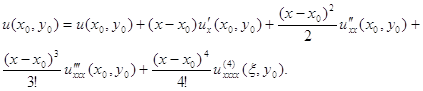
Для того, щоб оцінити похибку 2-ої похідної заміняємо  в першій заміні, у другій заміні .

Отже, для

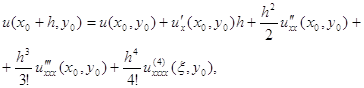
а для

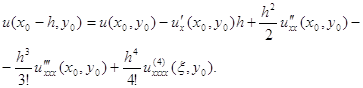
Користуючись цими розкладаннями, одержимо

Аналогічну формулу можна записати для похідної по у.

.

Аналогічно можна одержати оцінки для інших похідних.

Метод сіток

Ідея методу сіток відома давно ще за часів Ейлера. Однак, практичне використання цього методу наштовхувалося на серйозні труднощі, тому що одержання з його допомогою досить точного розв’язку крайової задачі звичайно приводило до колосальних систем алгебраїчних рівнянь, на розв’язок яких при ручному розрахунку були потрібні роки. Положення різко змінилося з появою електронних обчислювальних машин. Метод сіток допускає зручну реалізацію на ЕОМ, тому що застосування його зазвичай зводиться до масової повторюваності однорідних циклів. В даний час метод сіток є одним з найбільш ефективних методів розв’язку лінійних диференціальних рівнянь. Метод сіток (інакше метод скінчених різниць) для наближеного розв’язку крайових задач двовимірних диференціальних рівнянь полягає в наступному:

У плоскій області G, у якій розшукується розв’язок, будується сіткова область Gh, що складається з однакових осередків і наближає дану область G;

Задане диференціальне рівняння заміняється у вузлах побудованої сітки відповідним скінчено-різницевим рівнянням;

На підставі граничних умов установлюються значення шуканого розв’язку в граничних вузлах області Gh

Розв’язавши отриману систему скінчено-різницевих рівнянь, ми знайдемо значення шуканої функції у вузлах сітки, тобто будемо мати чисельний розв’язок нашої задачі. Вибір сіткової області здійснюється в залежності від конкретної задачі, але у всіх випадках контур Гh сіткової області Gh варто вибирати так, щоб він якнайкраще апроксимував контур Г заданої області G. Сітка будується таким чином, щоб вузли (xi,yi) сітки Sh або належали області G, або відстояли від її границі Г на відстань меншому, ніж h. Точки (вузли) сітки Sh називаються сусідніми, якщо вони розміщені один від одного в напрямку осі Ох або осі Оу на відстань, що дорівнює кроку сітки h. Вузол Ah сітки Sh називається внутрішнім, якщо він належить області G, а всі чотири сусідніх з ним вузла – множині Sh; інакше він називається граничним. Граничний вузол сітки Sh називається вузлом першого роду, якщо він має сусідній внутрішній вузол цієї сітки, інакше граничний вузол називається вузлом другого роду. Внутрішні вузли і граничні вузли першого роду сітки Sh називаються розрахунковими точками. Граничні вузли другого роду не входять в обчислення і можуть бути вилучені із сітки.

На перший погляд процедура застосування методу сіток, що складається з трьох етапів, може здатися простою і легко реалізованою. Однак насправді це не так. Через велику розмаїтість типів і розмірів сіток, видів рівнянь у часткових похідних, граничних і початкових умов, можливих кінцево-різницевих апроксимацій цих рівнянь і методів їхнього розв’язку, чисельне розв’язку рівнянь у часткових похідних вимагає модифікацій алгоритму при розгляді кожного конкретного приклада.

Стійкість скінчено-різницевої схеми для розв’язку рівнянь параболічного типу (рівняння теплопровідності)

Як приклад рівняння параболічного типу розглянемо рівняння теплопровідності:

,

де u=u(x,t) – температура, t – час,  - довжина стрижня.

Для простоти покладемо, а=1.

Початкові і крайові умови:

,

 и..

При використанні скінчено-різницевої схеми для розв’язку крайової задачі виникає питання про стійкість такої схеми. Під цим розуміють наступне: скінчено-різницева схема називається стійкою, якщо малі похибки в процесі розв’язку загасають або у всякому разі залишаються малими при необмеженому збільшенні номера поточного шару.

Для рівняння

                                           (3)

скінчено-різницева схема матиме вигляд:

.                   (4)

З'ясуємо умови стійкості з граничними і початковими умовами

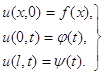                          (5)

Маємо:

 і ,

де , .

Переходячи до скінчених різниць у рівнянні (4), будемо мати:

=0  (6)

У граничних вузлах сітки Г виконані такі умови:

, , .

Припустимо, що в точках початкового шару t=0 допущена помилка , тобто

,

і нехай  - розв’язок рівняння (6):

. (7)

яке задовольняє граничним умовам, що містять помилку:

, , .

Нас цікавить, як зміниться похибка  при необмеженому зростанні номера j. Віднімаючи з рівняння (7) рівняння (6), для похибки  одержимо скінчено-різницеве рівняння.

=0.         (8)

На границі Г області маємо:

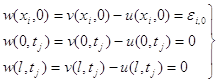             (8а)

Частковий розв’язок рівняння (8) будемо шукати у вигляді

,                            (9)

де числа  і p (р>0) підберемо так, щоб вираз (9) задовольняв рівнянню (8) і однорідним крайовим умовам.

.

Користуючись ними маємо:

,

звідки випливає, що pl=m і  (m=1,2,3……).

Отже,

.

Підставляючи цей вираз в рівняння (8), будемо мати:

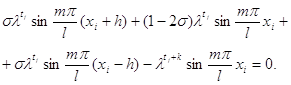         (10)

Після перетворень рівняння (10) набуде вигляду:

.

Звідси

. (11)

Зауважимо, що не залежить від точки (). Таким чином, для однорідного рівняння (8) одержуємо лінійно незалежні розв’язки вигляду:

 (m=1,2,…....,n-1),

причому кожен розв’язок задовольняє однорідним крайовим умовам.

Лінійна комбінація цих розв’язків

      (12)

також є розв’язком рівняння (8), що задовольняє при будь-яких значеннях коефіцієнтів  однорідним крайовим умовам. Ці коефіцієнти підбираються так, щоб виконувалася перша умова (8а), тобто щоб  (і=1,2,…...,n-1).

Для стійкості розглянутої скінчено-різницевої схеми (6) необхідно, щоб при будь-яких значеннях постійних  функція , обумовлена рівністю (12), залишалася обмеженою при .

Для цього досить, щоб для всіх m була виконана рівність:

.

Звідси

 і  (m=1,2,…...,n-1).

Остання нерівність буде виконана, якщо виконується умова:

.                                (13)

Отримані нерівності дають достатні умови стійкості розглянутої скінчено-різницевої схеми для змішаної задачі у випадку рівняння теплопровідності (параболічного типу).

Гіперболічний тип

Як приклад рівняння гіперболічного типу розглянемо рівняння коливань однорідної обмеженої струни:

,

де u=u(x,t) – зсув струни, t – час,  - координата довільної точки струни.

Для простоти покладемо, а=1.

Початкові і крайові умови:

.

 и.

Схема стійка, якщо виконано умову Куранта k< h. Це означає, що малі похибки, що виникають, наприклад, при обчисленні розв’язку на першому шарі, не будуть необмежено зростати при переході до кожного нового тимчасового шару. При виконанні умов Куранта схема має рівномірну збіжність, тобто при h® 0 розв’язок різницевої задачі рівномірно прагне до розв’язку вихідної змішаної задачі.

Недолік схеми в тім, що як тільки обрана величина кроку сітки h у напрямку x, з'являються обмеження на величину кроку  за змінною t. Якщо необхідно зробити обчислення для великого значення величини T, то може знадобитися велика кількість кроків по змінній t. Зазначений недолік характерний для всіх явних різницевих схем.

Еліптичний тип

Як приклад рівняння еліптичного типу розглянемо задачу Дирихле (перша крайова задача для рівняння Лапласа ):

,

Крайова умова:

на колі  (Г) виконується .

Перепишемо систему рівнянь у вигляді, зручному для застосування методу простої ітерації:

для внутрішніх вузлів

ui,k= - (14)

для граничных вузлів

 (15)

Тут для внутрішніх вузлів використовувався п’ятиточковий шаблон, зображений. Припустимо, що gi,k<0. Розв’яжемо систему рівнянь відносно ui,k методом простої ітерації згідно з ітераційним процесом:

для внутрішніх вузлів

для граничних вузлів

р=0,1,2,…,задане.

Доведено, що якщо gi,k<0, то послідовні наближення  збігаються до точного розв’язку різницевої схеми ui,k або системи рівнянь (14), (15) і має місце оцінка

max  

i,k i,k

де q=max .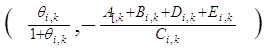

i,k

Доведення цього твердження полягає в перевірці умови збіжності методу простої ітерації для системи лінійних рівнянь, при цьому мається на увазі, що невідомий вектор утворює елементи ui,k. Наприклад, компоненти вектора можна перенумерувати таким чином: нехай  тоді

x1= u1.1, x 2 =u 2.1,…, x N1 = u N1.1;

x N1+1=u 2.1 x N1+2 =u 2.2,…, x 2N1 =u N1.2;

…………………………x N1N2 =u N1N2.

Відносно вектора =  різницева схема є системою лінійних рівнянь в матричному записі  де матриця А має в кожному рядку не більше п’яти елементів

  .........

  ........

А=... ...   .. ...

... ...   .. ...

.........  

Це пов’язано з тим, що похідні в кожному внутрішньому вузлі (i,k) апроксимувались за п’ятьма сусідніми вузлами.

 Розв’язання різницевих рівнянь при h 0 збігається до точного розв’язання крайової задачі зі швидкістю, яка визначається порядком апроксимації рівнянь та крайових умов. Таким чином, для точного розв’язання (u(x,y)) оцінки похибки

 max O(h2), h 0 (16)

i, k

Оцінка похибки (16) є справедливою, якщо точний розв’язок неперервно диференційований чотири рази в області G. Для областей з кутовими точками, наприклад прямокутника, взагалі кажучи, u(x,y) . Але якщо гранична функція, тобто  задовольняє в кутах спеціальні умови узгодження, то точний розв’язок u(x,y)  і є вірною оцінка (16).

Для прямокутної області G= такими умовами узгодження можуть бути:

достатня гладкість ;

функція повинна задовольняти в кутах прямокутника диференціальне рівняння.

Оцінка похибки (8.96) має в основному теоретичне значення, оскільки містить константу С, яку практично важко визначити

max ch2+ O(h2), h 0

i, k

Тому в реальних розрахунках використовується правило Рунге оцінки похибки, аналогічне тому, яке використовується в чисельному розв’язанні задачі Коші і розв’язанні звичайних диференціальних рівнянь. Робиться два варіанти розрахунку  з кроком h та ; тоді похибка має вигляд

max  max +О(h2)

і головна частина похибки визначається на вузлах,що збігаються.

Потрібно зазначити,що рівномірними прямокутними сітками найбільш зручно користуватиcя при розв’язанні задач у прямокутних областях. Якщо область має форму паралелограма(скошена система),то користуються координатами,осі яких паралельні сторонам цього паралелограма. Декартові прямокутні координати пов’язані з косокутними координатами  співвідношеннями , де а - кут між . У диференціальних виразах похідні за х та у замінюються похідними за . Усі похідні апроксимуються за допомогою центральних різниць. Якщо область має форму кола, зручно користуватись полярними координатами

Наведемо деякі загальні зауваження. При чисельному розв’язанні крайових задач для диференціальних рівнянь в частинних похідних методом сіток можуть бути використані тільки різницеві схеми, які збігаються, оскільки в цьому разі можна розраховувати на отримання наближеного розв’язку задачі, достатньо близького до точного. Але й різницеві схеми, що збігаються не завжди можуть бути використані при практичному розв’язанні задачі, оскільки при використанні методу сіток при обчисленні значень граничних функцій та правої частини виникають похибки. Щоб ці похибки не спотворили істинного розв’язання різницевої схеми, остання повинна бути стійкою за граничними умовами і за правою частиною. При використанні нестійкої різницевої схеми спотворення істинного розв’язку тим сильніше, чим дрібніша сітка; при використанні ж великої сітки не можна розраховувати на те, що розв’язок різницевої схеми буде близький до точного розв’язку крайової задачі для диференціального рівняння в силу поганої різницевої апроксимації рівняння.

Крім того, під час розв’язання різницевої задачі в процесі розрахунків нам обов’язково доведеться округляти значення розв’язків у вузлах сітки. Ці помилки можуть значно спотворити картину розв’язання, тому необхідною вимогою є стійкість різницевої схеми що до помилок, які виникають в результаті округлення значень розв’язку у вузлах сітки. Оскільки помилки округлення значень розв’язку в вузлах сітки, принаймні, в найпростіших випадках можна компенсувати зміною правої частини різницевого рівняння, то особливо суттєвою є вимога до стійкості правої частини. Необхідно взяти до уваги й числовий алгоритм, який використовується для розв’язання різницевої схеми. Навіть у випадку, коли різницева схема стійка за граничними умовами і за правою частиною, при невдалому виборі алгоритму для розрахунку розв’язання цієї різницевої схеми може відбутися сильне накопичення обчислювальної похибки, у цьому разі нестійким буде сам процес розрахунку. Нестійкі алгоритми розрахунку практично непридатні у випадку дрібної сітки.

Вибір оптимального кроку

Припустимо, що межа абсолютної погрішності при обчисленні функції  в кожній точці задовольняє нерівність

 (17)

Хай в деякій околиці крапки  похідні, через які виражаються залишкові члени, безперервні і задовольняють нерівностям

 (18)

де  - деякі числа. Тоді повна погрішність (без урахування погрішностей округлення) не перевершує відповідно величин

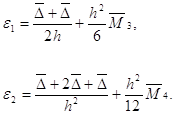
Мінімізація по  цих величин приводить до наступних значень:

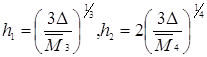 (19)

при цьому

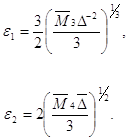 (19а)

Якщо при вибраному для якої-небудь значенні  відрізок не виходить за межі околиці точки, в якій виконується відповідна нерівність (17), то знайдене є оптимальним і повна погрішність чисельного диференціювання оцінюється відповідною величиною (19).

Дослідження точності

Дослідження точності одержаних виразів при чисельних розрахунках зручно робити за допомогою апостеріорної оцінки, по швидкості убивання членів відповідного ряду Тейлора. Якщо крок сітки достатньо малий, то погрішність близька до першого відкинутого члена.

Таким чином порядок точності результату по відношенню до кроку сітку рівний числу залишених в ній членів, або іншими словами, він рівний числу вузлів інтерполяції мінус порядок похідної. Тому мінімальне число вузлів необхідне для обчислення m-ой похідної, рівне m+1; воно забезпечує перший порядок точності.

Ці висновки відповідають принципу: при почленном диференціюванні ряду швидкість його збіжності зменшується.

Якщо врахувати погіршення збіжності ряду при диференціюванні, то можна зробити висновок: навіть якщо функція задана добре складеною таблицею на досить докладній сітці, то практично чисельним диференціюванням можна визначити першу і другу похідні, а третиною і четвертую – лише задовільно. Більш високі похідні рідко вдається обчислити із задовільною точністю.

Структура похибки розв'язку задачі

Побудувавши математичну модель, намагаються знайти її розв'язок. Для складних прикладних задач, як правило, не існує точного розв'язку у вигляді явних формул або скінченої послідовності арифметичних операцій, кожна з яких виконується точно. Тоді вдаються до чисельних методів — могутнього математичного засобу розв'язування задач. Найпростіші чисельні методи виникли і широко використовувалися задовго до появи ЕОМ. Але є багато прикладних задач, для яких знайти розв'язок без застосування ЕОМ практично неможливо. Сучасні швидкодіючі ЕОМ стали стимулом для розробки нових чисельних методів.

Застосовувати чисельні методи для розв'язування прикладних задач на базі ЕОМ треба обережно, оскільки точність знайденого розв'язку залежить від багатьох факторів. При цьому слід уміти оцінити похибку обчисленого розв'язку.

Похибка розв'язку задачі складається з похибки математичної моделі, неусувної похибки, похибки методу і обчислювальної похибки.

Похибка математичної моделі пов'язана з тим, що модель описує явище наближено, з припущеннями і спрощеннями. Тому треба мати уявлення про точність кінцевого результату, щоб спростити побудову математичної моделі.

Неусувна похибка зумовлена похибками у вхідних даних задачі. Вона залежить від методу розв'язування задачі. Але, щоб правильно обрати метод і визначити точність обчислень, важливо знати межі неусувної похибки.

Похибка методу пов'язана з необхідністю заміни неперервної моделі дискретною або з обривом нескінченного ітераційного процесу після скінченої кількості ітерацій.

Знайти чисельно розв'язок у(х) в усіх точках відрізка [а;b] неможливо, оскільки їх безліч. Тому на відрізку [а;b] беруть скінчену кількість точок (хі = a+ih, i = 0,1.....п, а + пh<=b<a +(п + 1)h) і тільки

в них знаходять значення у(х). Початкове значення y(a)=y0 нам відоме. Для знаходження інших значень уi= у(хі) (i = 1,2,.., n) диференціальне рівняння розглядають не на всьому відрізку [a;b], а тільки в зазначених точках y’(xi)=f(xi,y(xi)).

Замінивши похідну у'(х) її наближеним значенням (уi+1 - уі)/h, дістають систему рівнянь

уi+1 - уі = пf(хі, уі), i = 0,1,2,...,n-1. (20)

Звідси послідовно знаходять y1, y2,… yn.

Якщо в рівняння (20) замість уi i уi+1 підставити точні значення розв'язку у(хi) і y(xi+i)> то рівності задовольняться лише наближено.

Похибку, яку дістають від заміни неперервної моделі дискретною, називають похибкою дискретизації (або похибкою апроксимації),

Крім похибки дискретизації, існує інший тип похибки чисельних методів. В основі багатьох методів лежить ідея ітераційного процесу, в ході якого будується за певним правилом послідовність наближень до розв'язку задачі. Якщо ця послідовність має границю, коли кількість членів послідовності прямує до нескінченності, тоді ця границя буде розв'язком даної задачі. Але на ЕОМ можна обчислити тільки скінчену кількість членів послідовності. Похибку, спричинену обривом ітераційного процесу, називають похибкою збіжності. Похибку методу намагаються звести до величини, яка в кілька разів менша від похибки вхідних даних.

Отже, похибку чисельного методу можуть утворювати похибки дискретизації або похибки збіжності, або ж для деяких методів обидва типи похибок одночасно. Всі ці похибки, а також методи їх аналізу і регулювання розглядаються при побудові конкретних чисельних методів.

Обчислювальні похибки пов'язані з похибками округлення чисел. Обчислення, як ручні, так і на ЕОМ, виконують з певною кількістю значущих цифр. Це вносить у, результат похибку округлення, яка нагромаджується в ході обчислень. Похибки округлення можуть по-різному впливати на кінцевий результат. У результаті виконання мільйонів операцій, кожна з яких вносить невелику похибку, сумарна похибка округлень може значно перевищити шуканий результат обчислень. Але в окремих операціях похибки округлень можуть мати різні знаки і частково компенсувати одна одну. Тому, якщо немає систематичних причин, випадкове нагромадження похибок округлення незначне.

Систематичною причиною нагромадження похибок є, наприклад, віднімання близьких за величиною чисел, оскільки при малій абсолютній похибці чисел х1 і х2 відносна похибка (∆x1+∆x2)/|x1-x2| результату може стати великою.

Обчислювальні похибки виникають і під час перетворення чисел з однієї системи числення в іншу, якщо основа однієї системи числення не є степенем основи іншої. Це може призвести до того, що в новій системі числення число стане ірраціональним.

Втрата точності може статися і при додаванні до великого числа дуже малих чисел. Для зменшення похибки додавати числа варто в порядку їх зростання. У машинній арифметиці комутативний і дистрибутивний закони алгебри не завжди виконуються. Обчислювальний алгоритм треба будувати так, щоб похибка округлень була значно меншою від усіх інших похибок.

Поняття стійкості та коректності

Похибки у вхідних даних задачі — неусувні. Обчислювач не може їх зменшити, але мусить знати, як вони впливають на точність кінцевого результату. Одні задачі мають похибку результату такого самого порядку, як і порядок похибки вхідних даних, в інших задачах похибка результату може на кілька порядків перевищувати похибку вхідних даних. Чутливість задачі до неточностей у вхідних даних характеризується поняттям стійкості.

Задача називається стійкою за вхідними даними, якщо її розвязок неперервно залежить від вхідних даних, тобто малому приросту ∆х вхідної величини відповідає малий приріст ∆у шуканого розв'язку. Іншими словами, малі похибки вхідних даних спричинюють малі похибки розв'язку задачі. Якщо ця умова не виконується, то задача вважається нестійкою за вхідними даними. Це означає, що навіть незначні похибки вхідних даних можуть привести до як завгодно великих похибок розв'язку, тобто розв'язок може бути зовсім спотворений. Тому застосовувати безпосередньо до таких задач чисельні методи не можна, оскільки похибки округлень при застосуванні методу будуть катастрофічно нагромаджуватись у ході обчислень. Наведемо приклад нестійкої задачі, який належить Уілкінсону.

Введемо тепер поняття коректності задачі.

Задача називається коректно поставленою, якщо для будь-яких вхідних даних з деякого класу існує єдиний і стійкий за вхідними даними її розв'язок.

Для розв'язування некоректно поставлених задач застосовувати класичні чисельні методи не варто, оскільки похибки округлень при розрахунках можуть катастрофічне зростати і призвести до результату, далекого від шуканого розв'язку. Для розв'язування некоректно поставлених задач використовують так звані методи регуляризацїї, які замінюють дану задачу коректно поставленою.

Програмна реалізація

Розглянемо приклад рівняння в частинних похідних гіперболічного типу

Область:

Початкові умови:

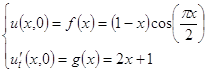
Граничні умови:

Крок по осі Х: hx=0,1

Крок по осі Y: hy=0,05

Реалізуємо в Pascal

Const

n = 10;

m = 10;

hx = 1/n;

hy = 0.05;

l = hy/hx;

Var

u:Array [0..n,0..m] of Real;

i,j:Integer;

fo:Text;

Function f(x:Real):Real;

begin

f:=(1-x)*cos(Pi*x/2);

end;

Function g(x:Real):Real;

begin

g:=2*x+1;

end;

Function fi(y:Real):Real;

begin

fi:=2*y+1;

end;

Function psi(t:Real):Real;

begin

psi:=0;

end;

Begin

For i:=1 to n-1 do begin

u[i,0]:=f(i*hx);

u[i,1]:=f(i*hx)+hy*g(i*hx);

end;

For j:=0 to m do begin

u[0,j]:=fi(j*hy);

u[n,j]:=psi(j*hy);

end;

For j:=1 to m-1 do

For i:=1 to n-1 do

u[i,j+1]:=2*(1-sqr(l))*u[i,j]+sqr(l)*(u[i+1,j]+u[i-1,j])-u[i,j-1];

Assign(fo,'result.txt');

ReWrite(fo);

For j:=m downto 0 do begin

Write(fo,j*hy:4:2,' |');

For i:=0 to n do Write(fo,u[i,j]:8:4);

WriteLn(fo);

end;

For j:=1 to 94 do Write(fo,'-');

WriteLn(fo);

Write(fo,' y/x |');

For j:=0 to n do Write(fo,j*hx:8:4);

Close(fo);

End.

RESULT.txt

0.50 | 2.0000 1.8693 1.7537 1.6381 1.5294 1.4450 1.2724 0.9448 0.6245 0.3283 0.0000

0.45 | 1.9000 1.7551 1.6251 1.4873 1.3910 1.3473 1.2499 0.9784 0.6246 0.3280 0.0000

0.40 | 1.8000 1.6447 1.4945 1.3467 1.2658 1.2361 1.1839 0.9914 0.6389 0.3198 0.0000

0.35 | 1.7000 1.5355 1.3646 1.2229 1.1533 1.1193 1.0828 0.9644 0.6616 0.3114 0.0000

0.30 | 1.6000 1.4248 1.2419 1.1171 1.0498 1.0019 0.9612 0.8913 0.6724 0.3127 0.0000

0.25 | 1.5000 1.3121 1.1338 1.0257 0.9511 0.8863 0.8323 0.7809 0.6480 0.3258 0.0000

0.20 | 1.4000 1.2018 1.0433 0.9427 0.8549 0.7734 0.7041 0.6502 0.5763 0.3380 0.0000

0.15 | 1.3000 1.1015 0.9672 0.8628 0.7602 0.6636 0.5797 0.5145 0.4635 0.3252 0.0000

0.10 | 1.2000 1.0172 0.8986 0.7834 0.6670 0.5569 0.4600 0.3823 0.3289 0.2658 0.0000

0.05 | 1.1000 0.9489 0.8308 0.7037 0.5754 0.4536 0.3451 0.2562 0.1918 0.1556 0.0000

0.00 | 1.0000 0.8889 0.7608 0.6237 0.4854 0.3536 0.2351 0.1362 0.0618 0.0156 0.0000

y/x | 0.0000 0.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 0.9000 1.0000

Для дослідження збіжності розв’язку даної задачі, змінимо крок розбиття сітки. Наприклад, візьмемо крок, в двічі менший, як по осі X, так і осі Y і знайдемо розв’язок за допомогою цієї ж програми.

Отримаємо:

0.50 | 2.0000 1.7347 1.5044 1.2505 0.6479 0.0000

0.40 | 1.8000 1.4766 1.2682 1.1311 0.6793 0.0000

0.30 | 1.6000 1.2472 1.0499 0.9330 0.6538 0.0000

0.20 | 1.4000 1.0568 0.8517 0.6944 0.5347 0.0000

0.10 | 1.2000 0.9008 0.6654 0.4551 0.3218 0.0000

0.00 | 1.0000 0.7608 0.4854 0.2351 0.0618 0.0000

-----------------------------------------------------------------

y/x | 0.0000 0.2000 0.4000 0.6000 0.8000 1.0000

Крок був взятий так, щоб можна було порівняти розв’язок в окремих вузлах, як в першому, так і в другому випадку. Методом порівняння можна побачити, що розв’язок в вузлах сітки дещо відрізняється. З цього можна зробити висновок, що на збіжність розв’язку також впливає такий фактор, як крок розбиття сітки.

Виконаємо також обчислення в середовищі Excel і порівняємо отримані дані.

З отриманого результату, що наведений дещо нижче, можна зробити висновок, що отримані дані співпадають, що свідчить о вірності розв’язку задачі, хоча і мають різну точність, що пов’язана з точністю обчислення (в Pascal точність залежить від типу змінної).

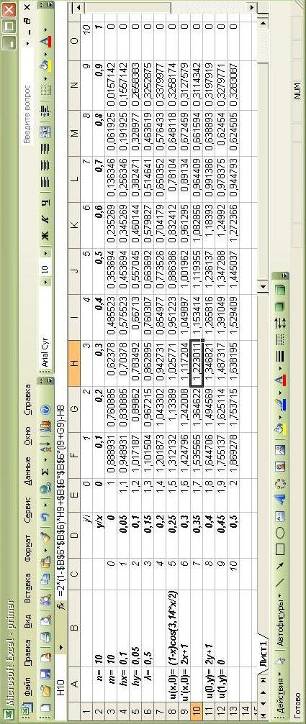
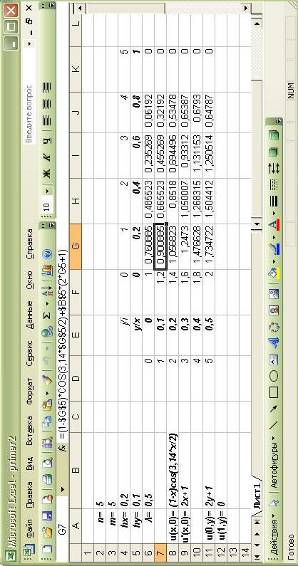
Узгодженість і збіжність

Різницева схема, що сходиться, повинна давати рішення, яке прагне істинного рішення ДР при подрібненні сітки. Порушення збіжності може бути обумовлено наступними причинами:

Неузгодженість PC з початковим ДР. При подрібненні сітки значення шуканої функції при заданих незалежних змінних прагне певної межі. але ця межа не співпадає з істинним рішенням.

Нестійкість PC. При подрібненні сітки значення шуканої функції при заданих незалежних змінних не прагне певної межі. У будь-якому випадку в ході обчислювального експерименту нестійкість проявляє себе як швидке, катастрофічне наростання чисел.

Математичні основи питань збіжності добре розвинені тільки для лінійних ДР. Результати лінійної теорії використовуються у вигляді навідних міркувань для нелінійних задач, а їх застосовність перевіряється потім в ході обчислювального експерименту. Для лінійних ДУ в ЧП існує т.н, теорема Лакса, яка говорить, що за наявності стійкості апроксимація є необхідною і достатньою умовою збіжності PC.

апроксимація + стійкість => збіжність PC

У вживанні до нелінійних ДР в ЧП використовування теореми Лакса припускає використовування принципу "заморожених" коефіцієнтів. Під методом "заморожених" коефіцієнтів розуміють простий прийом, коли коефіцієнти в ДР замінюють деякими константами і аналізують одержане ДУ з постійними коефіцієнтами. Якщо аналіз показує нестійкість PC для "заморожених" коефіцієнтів, то таку схему виключають з розгляду. Якщо ж схема для рівняння з "замороженими" коефіцієнтами буде злагодженою і стійкою, тобто надія, що ця схема буде тією, що сходиться і для нелінійного ДР.

Так, щоб бути упевненим, що PC, що використовується, дає рішення, що сходиться при подрібненні сітки до істинного рішення початкового ДР, необхідно довести її узгодженість і стійкість.

Погрішність апроксимації

PC апроксимації ДР злагоджена з початковим ДР (або апроксимує ДР), якщо в межі, коли розміри осередків сітки прагнуть нуля, PC еквівалентна даному ДР в кожній з вузлових точок, тобто

PC і ДР при цьому записують, перекидаючи всі члени в одну сторону (щоб з другого боку залишився нуль).

Кількісною характеристикою узгодженості є погрішність (помилка) апроксимації ДР даної PC

Е=(РС-ДУ).

В термінах погрішності апроксимації: PC злагоджена з своїм ДР, якщо погрішність апроксимації у всіх вузлах сітки прагне нуля при будь-якому подрібненні кроків сітки.

Провідні члени погрішності називаються порядком апроксимації ДР даної PC.

Як правило:

• для тих PC, що сходяться помилка чисельного рішення зменшується подібно погрішності апроксимації;

• порядок апроксимації ДР (провідні члени погрішності апроксимації) визначається порядком точності формул, використаних для апроксимації похідних;

• для злагоджених явних PC можна встановити співвідношення між кроками сітки, при виконанні якого досягається більш високий порядок апроксимації.

Висновок

Диференціальні рівняння в частинних похідних є широко вживаним математичним апаратом при розробці моделей в самих різних областях науки і техніки. На жаль, явне рішення цих рівнянь в аналітичному вигляді виявляється можливим тільки в окремих простих випадках, і, як результат, можливість аналізу математичних моделей, побудованих на основі диференціальних рівнянь, забезпечується за допомогою наближених чисельних методів рішення. Об'єм виконуваних при цьому обчислень звичайно є значним і використовування високопродуктивних обчислювальних систем є традиційним для даної області обчислювальної математики. Проблематика чисельного рішення диференціальних рівнянь в частинних похідних є областю інтенсивних досліджень.

Стосовно самої теми курсової роботи, треба відзначити, що збіжність рішень ДРЧП досягається, в першу чергу через теорему Лакса – апроксимація + стійкість породжує збіжність. Також треба зазначити, що на збіжність також впливає, хоча і в меншій мірі, вибір кроку розбиття сітки, а також різноманітні похибки, хоча вони і не значно впливають на розв’язок, проте дещо спотворюють його. Тому, щоб досягти найбільш точного і оптимального рішення потрібно враховувати всі фактори, що можуть впливати на збіжність і точність даного розв’язку.

Література

Ляшенко М.Я., Головань М.С. Чисельні методи.-К.: Либідь, 1996.-288с.

http://www.software.unn.ac.ru/ccam/files/HTML_Version/index.php

http://www.arptek.ru/i18n

Лекції по чисельним методам Л.Д. Назаренко.

http://www.ict.nsc.ru/rus/texbooks/akhmerov/matmodel/2-4-7.php

http://www.nsc.ru/rus/textbooks/akhmerov/ode/s-33/s-33.php