Курсовая работа: Еліптичні інтеграли
Міністерство освіти і науки України
Південноукраїнський державний педагогічний університет
ім. К.Д.Ушинського (м. Одеса)
Кафедра математичного аналізу
Курсова робота на тему:
„Еліптичні інтеграли”
виконала
студентка 4 курсу
інституту фізики і математики
спеціальності „МІ”
Сушкова О.А.
Науковий керівник:
Аров Д.З.
Одеса 2007
План
Вступ
1. Загальні зауваження та означення
2. Допоміжні перетворення
3. Приведення до канонічної форми
4. Еліптичні інтеграли 1-го, 2-го і 3-го роду
Висновки
Література
Додатки
Вступ
У багатьох питаннях науки і техніки доводиться не по заданій функції шукати її похідну, а навпаки – відновлювати функцію по відомій її похідній.
Дамо наступне означення:
Функція F(x) на даному проміжку називається первісною функцією для функції f(x) або інтегралом від f(x), якщо на всьому цьому проміжку f(x) являється похідною для функції F(x) або, що те ж саме, f(x)dx служить для F(x) диференціалом
F’(x )= f(x) або dF(x )= f(x)dx.
Пошук для функції всіх її первісних, що називається інтегруванням її, і складає одну з задач інтегрального числення; як бачимо, ця задача являється оберненою основній задачі диференціального числення. Так, наприклад, для обчислення довжини дуги еліпса чи деякої її частини необхідно розв’язати певні еліптичні інтеграли, яким і присвячена дана курсова робота.
1. Загальні зауваження та означення
Розглянемо інтеграл виду
![]() (1)
(1)
де y це алгебраїчна функція від х, тобто задовольняє алгебраїчному рівнянню
![]() (2)
(2)
(тут ![]() - цілий відносно
- цілий відносно ![]() та
та ![]() многочлен). Інтеграли подібного роду
отримали назву абелевих інтегралів. До їх числа відносяться інтеграли
многочлен). Інтеграли подібного роду
отримали назву абелевих інтегралів. До їх числа відносяться інтеграли

![]()
![]()
Дійсно, функції

![]()
задовольняють, відповідно, алгебраїчним рівнянням
![]()
![]()
Виходячи на геометричну точку зору, абелев інтеграл (1) вважають зв’язаним з тою алгебраїчною кривою, яка визначається рівнянням (2). Наприклад, інтеграл
![]() (3)
(3)
зв’язаний з
кривою другого порядку ![]()
Якщо крива (2) може бути представлена параметрично
![]()
![]()
так, що функції ![]()
![]() є раціональними, то в
інтегралі (1) стає можливою раціоналізація підінтегрального виразу: підстановкою
є раціональними, то в
інтегралі (1) стає можливою раціоналізація підінтегрального виразу: підстановкою
![]() вона
зводиться до виду
вона
зводиться до виду
![]() .
.
До цього класу відносяться обидва вище згадані випадки. В окремому випадку, можливість раціоналізації підінтегрального виразу в інтегралі типу (3) зв’язана безпосередньо з тим фактом, що крива другого порядку унікурсальна.
Очевидно, що змінні x і t зв’язані алгебраїчним рівнянням, так що t являється алгебраїчною функцією від х. Якщо розширити клас елементарних функцій, включаючи в нього і всі алгебраїчні функції, то можна сказати, що в випадку унікурсальності кривої (2), інтеграл (1) завжди виражається через елементарні функції в кінцевому виді.
Але подібні обставини являються в деякому розумінні винятком. В загальному випадку крива (2) не унікурсальна, тоді ж, як можна довести, інтеграл (1) заздалегідь не завжди, тобто не при всякій функції R, може бути вираженим в кінцевому виді (проте не виключена можливість цього при окремих конкретних R).
З цим ми зустрічаємося уже при розгляді важливого класу інтегралів
![]() (4)
(4)
![]()
які містять квадратний корінь з многочленів 3-ої або 4-ої степені і звичайно прилягаючих до інтегралів (3). Інтеграли виду (4) , як правило , уже не виражаються в кінцевому вигляді через елементарні функції навіть при розширеному розумінні цього терміну. Тому, знайомство з ними ми віднесли до заключного параграфу, щоб не переривати головної лінії викладення даної глави, присвяченої, головним чином вивченню класів інтегралів, що беруться в кінцевому вигляді.
Многочлени під коренем в (4) передбачаються такими, що мають дійсні коефіцієнти. Крім того, ми завжди будемо вважати, що у них не має кратних коренів, бо інакше, можна було б винести лінійний множник з під знаку кореня; питання звелося б до інтегрування виразу раніше вивчених типів, і інтеграл виразився б у кінцевому вигляді. Кінцева обставина може мати місце інколи і при відсутності кратних коренів; наприклад, легко перевірити, що


Інтеграли від виразів типу (4) взагалі називають еліптичними в зв’язку з тією обставиною, що вперше з ними зіткнулися при розв’язанні задачі про спрямування еліпсу:
Еліпс: 
Зручніше буде
взяти рівняння еліпса в параметричній формі ![]() ,
, ![]() . Очевидно,
. Очевидно,
![]()
де  - числовий
ексцентриситет еліпса.
- числовий
ексцентриситет еліпса.
Обчислюючи довжину дуги еліпса від верхнього кінця малої осі до будь-якої його точки в першому квадранті, отримаємо
 ,
,
Таким чином, довжина дуги еліпса виражається еліптичним інтегралом 2-го роду; як вказувалося, цей факт послужив поводом для самої назви „еліптичний”.
В частковому випадку, довжина чверті обводу еліпса виражається через повний еліптичний інтеграл
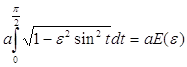 .
.
Між іншим, цю назву, в прямому розумінні, відносять зазвичай лише до таких із них, що не беруться в кінцевому вигляді; інші ж, подібні тільки що приведеним, називають псевдоеліптичними.
Вивчення і табулювання ( тобто складання таблиць значень) інтегралів від виразів (4) при довільних коефіцієнтах a, b, c,…, розуміється складно. Тому звичайно бажання звести всі ці інтеграли, до небагатьох таких, до складу яких входило б по можливості менше довільних коефіцієнтів (параметрів).
Це досягається за допомогою елементарних перетворень, які ми розглянемо в наступних пунктах.
2. Допоміжні перетворення
Зазначимо перш за все, що достатньо обмежитися випадком многочлена 4-ї степені під коренем, так як до нього легко приводиться випадок, коли під коренем многочлен 3-ї степені.
Розглянемо, взагалі, алгебраїчне рівняння непарної степені (з дійсними коефіцієнтами)
![]() .
.
При достатньо
великих по абсолютній величині значеннях x многочлен має знак старшого члена,
тобто при додатному x – знак ![]() , а при від’ємному x – обернений знак. Так, як многочлен
це неперервна функція, то, міняючи знак, він в проміжній точці необхідно
перетворюється в 0. Звідси: всяке алгебраїчне рівняння непарної степені (з
дійсними коефіцієнтами) має принаймні один дійсний корінь.
, а при від’ємному x – обернений знак. Так, як многочлен
це неперервна функція, то, міняючи знак, він в проміжній точці необхідно
перетворюється в 0. Звідси: всяке алгебраїчне рівняння непарної степені (з
дійсними коефіцієнтами) має принаймні один дійсний корінь.
Дійсно, многочлен
3-ї степені ![]() з дійсними коефіцієнтами
необхідно має дійсний корінь, скажемо λ, і, відповідно, допускає дійсне
розкладання
з дійсними коефіцієнтами
необхідно має дійсний корінь, скажемо λ, і, відповідно, допускає дійсне
розкладання
![]()
Підстановка ![]() ( або
( або ![]() ) і здійснює потрібне приведення
) і здійснює потрібне приведення
![]()
В першу чергу ми будемо розглядати лише диференціали, що мають корінь із многочленів 4-ї степені.
По відомій теоремі алгебри, многочлен четвертої степені з дійсними коефіцієнтами може бути представленим у виді добутку двох квадратних трьохчленів з дійсними коефіцієнтами:
![]() (5)
(5)
Постараємось тепер необхідною підстановкою знищити в обох трьохчленах відразу члени першої степені.
Якщо р = р’, то наша ціль досягається простою підстановкою ![]() . Нехай тепер
. Нехай тепер ![]() ; в цьому випадку ми
скористаємось дробно-лінійною підстановкою
; в цьому випадку ми
скористаємось дробно-лінійною підстановкою

Можливість встановити дійсні і при чому різні значення для коефіцієнтів μ і ν зумовлена нерівністю
![]() (6)
(6)
Нехай же тепер трьохчлени (5) обидва мають дійсні корені, скажемо, перший – корені α і β, а другий корені γ і δ. Підставляючи
![]()
![]()
![]()
![]()
можна переписати (6) у вигляді
![]() (6´)
(6´)
а для здійснення цієї нерівності достатньо лише потурбуватися, щоб корені трьохчленів не перемежались (наприклад, щоб було α > β > γ > δ ), що в наших можливостях.
Таким чином, належно вибравши μ і ν, за допомогою вказаної підстановки ми отримаємо
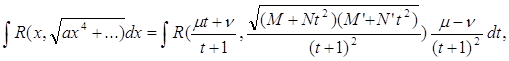
що можна також (якщо виключити випадки, коли який-небудь з коефіцієнтів M, N, M’, N’ виявляються нулем) переписати у виді
![]()
при А, m і m’ відмінних від нуля.
Цей інтеграл можна звести, з точністю до інтеграла від раціональної функції, до такого

Розкладемо тепер раціональну функцію R*(t) на два доданки

Перший доданок не
міняє свого значення при заміні t на –t, значить, зводиться до раціональної
функції від ![]() :
:
![]() ; другий
же при вказаній заміні міняє знак, і тому має вид
; другий
же при вказаній заміні міняє знак, і тому має вид ![]() Розглянутий інтеграл представиться в
формі суми інтегралів
Розглянутий інтеграл представиться в
формі суми інтегралів

Але другий із них
підстановкою ![]() відразу зводиться до елементарного
інтегралу
відразу зводиться до елементарного
інтегралу
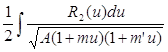
і береться в кінцевому виді. Таким чином, подальшому дослідженню підлягає тільки інтеграл
 (7)
(7)
3. Приведення до канонічної форми
Покажемо, нарешті, що кожен інтеграл типу (7) може бути представленим у формі
 (8)
(8)
де k – деякий додатній правильний дріб: 0<k<1. Назвемо цю форму канонічною.
Введемо скорочено
![]()
Не зменшуючи загальності, дозволяється вважати тут А = ± 1; крім того, для визначеності обмежимося додатніми значеннями t. Розглянемо тепер різні можливі комбінації знаків A, m, m’ і вкажемо для кожного випадку підстановку, що безпосередньо приводить інтеграл (7) в канонічну форму.
1)
А = +1, ![]()
![]() (
(![]() ). Для того, щоб радикал мав дійсні
значення, необхідно, щоб було
). Для того, щоб радикал мав дійсні
значення, необхідно, щоб було  або
або  Припускаємо, що
Припускаємо, що
![]() де 0<z<1 або
де 0<z<1 або 
Тоді

так, що за k тут треба прийняти ![]()
2) А = +1, ![]()
![]() (h, h’>0). Для того, щоб радикал мав дійсні значення, обмежимося
значеннями
(h, h’>0). Для того, щоб радикал мав дійсні значення, обмежимося
значеннями  .
.
Припускаємо, що
![]() де 0 < z ≤ 1.
де 0 < z ≤ 1.
Тоді

і можна взяти 
3) А = +1, ![]()
![]() (h>h’>0). Зміна t нічим не
обмежена. Припустимо
(h>h’>0). Зміна t нічим не
обмежена. Припустимо
 де 0≤z<1.
де 0≤z<1.
В цьому випадку

і ![]()
4) А = -1, ![]()
![]() (h, h’>0). Зміна t обмежена нерівністю
(h, h’>0). Зміна t обмежена нерівністю ![]() . Беремо
. Беремо
 , де 0<z<1 ,
, де 0<z<1 ,
так, що

і ![]() .
.
5) А = -1, ![]()
![]() (h>h’>0). Змінна t може змінюватися лише між
(h>h’>0). Змінна t може змінюватися лише між ![]() і
і ![]() . Припустимо
. Припустимо
 , де 0<z<1.
, де 0<z<1.
Маємо

і  Цим вичерпуються всі
можливі випадки, тому що у випадку, коли А = -1 і обидва числа m, m’ > 0, радикал взагалі не міг би мати дійсних значень. Про множник
Цим вичерпуються всі
можливі випадки, тому що у випадку, коли А = -1 і обидва числа m, m’ > 0, радикал взагалі не міг би мати дійсних значень. Про множник ![]() ми не говорили нічого, тому що у всіх
випадках він, очевидно, перетворювався у раціональну функцію від
ми не говорили нічого, тому що у всіх
випадках він, очевидно, перетворювався у раціональну функцію від ![]() .
.
Відмітимо ще, що
розглядаючи інтеграл (8), ми можемо обмежуватися значеннями z<1; випадок ![]() приводиться до цього
підстановкою
приводиться до цього
підстановкою ![]() , де
, де ![]() <1.
<1.
4. Еліптичні інтеграли 1-го, 2-го і 3-го роду
Тепер залишається вивчити найпростіші з інтегралів виду (8), до яких можна було б звести всі інтеграли цього виду, а відповідно, в кінцевому рахунку, і взагалі, всі еліптичні інтеграли.
Виділимо з
раціональної функції R(x), що зустрічається в
підінтегральному виразі (8) цілу частину P(x), а правильний дріб, який входить до
його складу, розкладемо на прості дроби. Якщо не об’єднувати спряжені
комплексні корені знаменника, а розглядати їх окремо, як дійсні корені, то R(x) представиться у вигляді суми
степенів ![]() (n = 0, 1, 2,…) і дробів виду
(n = 0, 1, 2,…) і дробів виду  (m = 1, 2, 3,…), де а може бути і уявним числом,
помножених на числові коефіцієнти. Звідси ясно, що інтеграл (8), в загальному
випадку, являється лінійним агрегатом наступних інтегралів:
(m = 1, 2, 3,…), де а може бути і уявним числом,
помножених на числові коефіцієнти. Звідси ясно, що інтеграл (8), в загальному
випадку, являється лінійним агрегатом наступних інтегралів:
 (n = 0, 1, 2,…)
(n = 0, 1, 2,…)
і![]()
 (m = 1, 2, 3,…).
(m = 1, 2, 3,…).
Зупинимося на
інтегралах ![]() .
Якщо проінтегрувати тотожність
.
Якщо проінтегрувати тотожність

то отримаємо рекурентне співвідношення
 (9)
(9)
що зв’язують три
послідовні інтеграли І. Припускаючи що тут n=2, виразимо ![]() через
через ![]() та
та ![]() ; якщо взяти n=3 і замість
; якщо взяти n=3 і замість ![]() підставити його вираз через
підставити його вираз через ![]() та
та ![]() , то навіть
, то навіть ![]() виразиться
через ці інтеграли. Продовжуючи так далі, легко переконатися, що кожен з
інтегралів
виразиться
через ці інтеграли. Продовжуючи так далі, легко переконатися, що кожен з
інтегралів ![]() виражається
через
виражається
через ![]() та
та ![]() і далі
враховуючи (9), можна встановити і вигляд з’єднуючої їх формули
і далі
враховуючи (9), можна встановити і вигляд з’єднуючої їх формули
![]()
де ![]() і
і ![]() - постійні, а
- постійні, а ![]() є непарний многочлен степені (2n-3). Звідси стає зрозумілим, що якщо
є непарний многочлен степені (2n-3). Звідси стає зрозумілим, що якщо ![]() є многочлен n – ї степені від х, то
є многочлен n – ї степені від х, то
 , (10)
, (10)
де ![]() і
і ![]() - постійні, а
- постійні, а ![]() (х) є деякий
многочлен (n-2) – ї степені від х. Визначення
цих постійних і коефіцієнтів многочлена Q може бути виконано (якщо многочлен Р
коректно заданий за методом невизначених коефіцієнтів.)
(х) є деякий
многочлен (n-2) – ї степені від х. Визначення
цих постійних і коефіцієнтів многочлена Q може бути виконано (якщо многочлен Р
коректно заданий за методом невизначених коефіцієнтів.)
Зауважимо, що з
(9) можна було б виразити через ![]() та
та ![]() інтеграли
інтеграли ![]() і при від’ємних значеннях (n = -1, -2, …), так що в інтегралах
і при від’ємних значеннях (n = -1, -2, …), так що в інтегралах ![]() досить обмежитись випадком
досить обмежитись випадком ![]() .
.
Переходячи до
інтегралів ![]() (скажімо,
при дійсних a), подібним чином встановимо
для них рекурентне співвідношення
(скажімо,
при дійсних a), подібним чином встановимо
для них рекурентне співвідношення

справедливе і при від’ємних і нульовому значеннях m.
Звідси всі ![]() виражаються
через три з них:
виражаються
через три з них:

тобто, кінцево
через ![]() ,
, ![]() та
та ![]() .
.
Підкреслимо, що усе це зберігає силу і при уявних значеннях параметра а.
Так в результаті усіх наших тверджень ми підходимо до наступних висновків: всі еліптичні інтеграли за допомогою елементарних підстановок – з точністю до доданків, що виражаються в кінцевому виді, - приводяться до наступних трьох стандартних інтегралів:

|

( останній
інтеграл виходить із ![]() введенням, замість
введенням, замість ![]() , нового параметра
, нового параметра  ). Ці
інтеграли, як показав Ліувіль , в кінцевому виді вже не беруться. Лежандр їх
назвав еліптичними інтегралами, відповідно, 1-го, 2-го і 3-го роду. Перші два
містять лише один параметр k, а останній, крім нього, ще
(комплексний) параметр h.
). Ці
інтеграли, як показав Ліувіль , в кінцевому виді вже не беруться. Лежандр їх
назвав еліптичними інтегралами, відповідно, 1-го, 2-го і 3-го роду. Перші два
містять лише один параметр k, а останній, крім нього, ще
(комплексний) параметр h.
Лежандр вніс у ці
інтеграли ще подальші спрощення, виконавши в них підстановку ![]() (
(![]() змінюється від 0 до
змінюється від 0 до ![]() ). При цьому перший із
них безпосередньо переходить в інтеграл
). При цьому перший із
них безпосередньо переходить в інтеграл
 . (11)
. (11)
Другий перетворюється так:
![]()

тобто приводиться до попереднього інтеграла і до нового інтеграла
![]() . (12)
. (12)
Нарешті, третій інтеграл при вказаній підстановці переходить в
 . (13)
. (13)
Інтеграли (11), (12) і (13) також називаються еліптичними інтегралами 1-го, 2-го і 3-го роду – в формі Лежандра.
Із них особливо
важливе значення і застосування мають перші два. Якщо враховувати, що ці
інтеграли при ![]() перетворюються в нуль, і тим зафіксувати
вільні сталі, що містяться в них, то отримаємо дві доволі визначені функції від
перетворюються в нуль, і тим зафіксувати
вільні сталі, що містяться в них, то отримаємо дві доволі визначені функції від
![]() , які
Лежандр позначив відповідно через F(k, φ)
і E(k, φ). Тут, крім незалежної
змінної
, які
Лежандр позначив відповідно через F(k, φ)
і E(k, φ). Тут, крім незалежної
змінної ![]() ,
вказаний також параметр k, що називається модулем, який входить у вирази цих функцій.
,
вказаний також параметр k, що називається модулем, який входить у вирази цих функцій.
Лежандром були
складені обширні таблиці значень цих функцій при різних ![]() і різних k. В них не тільки аргумент
і різних k. В них не тільки аргумент ![]() ,який
трактуються як кут, що виражається в градусах, але і модуль k розглядається як синус деякого кута
,який
трактуються як кут, що виражається в градусах, але і модуль k розглядається як синус деякого кута![]() , який і
вказується в таблиці замість модуля, причому також в градусах.
, який і
вказується в таблиці замість модуля, причому також в градусах.
Крім того, як Лежандром, так і іншими вченими були вивчені найглибші властивості цих функцій, встановлений ряд формул, що відносяться до них, і т.д.
Дякуючи цьому функції F і E Лежандра ввійшли в сім’ю функцій, що зустрічаються в аналізі і його додатках, на рівних правах з елементарними функціями.
Висновки
В результаті усіх наших міркувань ми коротко можемо сказати, що всі еліптичні інтеграли за допомогою елементарних підстановок – з точністю до доданків, що виражаються в кінцевому виді, - приводяться до наступних трьох стандартних інтегралів Лежандра:

|

А за допомогою
підстановки ![]() (
(![]() змінюється від 0 до
змінюється від 0 до ![]() ) ці інтеграли
перетворюються в такі:
) ці інтеграли
перетворюються в такі:
 ,
, ![]() і
і  ,
,
які також називаються еліптичними інтегралами 1-го, 2-го і 3-го роду в формі Лежандра, значення яких можна знайти в таблицях.
Використана література:
1. Г.М. Фихтенгольц. Курс дифференциального и интегрального исчисления. Том I. М.: Наука, 1966 г., 800 стр. с илл.
2. Г.М. Фихтенгольц. Курс дифференциального и интегрального исчисления. Том II. М.: Наука, 1966 г., 800 стр. с илл.
3. Г. Корн, Т. Корн. Справочник по математике для научных работников и инженеров. М.: Наука, 1973 г., 832 стр. с илл.
4. И.Н. Бронштейн, К.А. Семендяев. Справочник по математике для инженеров и учащихся вузов. М.: Наука, 1980 г., 976 с., илл.
ДОДАТКИ
Еліптичні інтеграли першого роду

|
Еліптичні інтеграли першого роду |
||||||||||
| 0° | 10° | 20° | 30° | 40° | 50° | 60° | 70° | 80° | 90° | |
| 0° | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 10 | 0.1745 | 0.1746 | 0.1746 | 0.1748 | 0.1749 | 0.1751 | 0.1752 | 0.1753 | 0.1754 | 0.1754 |
| 20 | 0.3491 | 0.3493 | 0.3499 | 0.3508 | 0.3520 | 0.3533 | 0.3545 | 0.3555 | 0.3561 | 0.3564 |
| 30 | 0.5236 | 0.5243 | 0.5263 | 0.5294 | 0.5334 | 0.5379 | 0.5422 | 0.5459 | 0.5484 | 0.5493 |
| 40 | 0.6981 | 0.6997 | 0.7043 | 0.7116 | 0.7213 | 0.7323 | 0.7436 | 0.7535 | 0.7604 | 0.7629 |
| 50 | 0.8727 | 0.8756 | 0.8842 | 0.8982 | 0.9173 | 0.9401 | 0.9647 | 0.9876 | 1.0044 | 1.0107 |
| 60 | 1.0472 | 1.0519 | 1.0660 | 1.0896 | 1.1226 | 1.1643 | 1.2126 | 1.2619 | 1.3014 | 1.3170 |
| 70 | 1.2217 | 1.2286 | 1.2495 | 1.2853 | 1.3372 | 1.4068 | 1.4944 | 1.5959 | 1.6918 | 1.7354 |
| 80 | 1.3963 | 1.4056 | 1.4344 | 1.4846 | 1.5597 | 1.6660 | 1.8125 | 2.0119 | 2.2653 | 2.4362 |
| 90 | 1.5708 | 1.5828 | 1.6200 | 1.6858 | 1.7868 | 1.9356 | 2.1565 | 2.5046 | 3.1534 |
|
Еліптичні інтеграли другого роду

|
Еліптичні інтеграли другого роду |
||||||||||
| 0° | 10° | 20° | 30° | 40° | 50° | 60° | 70° | 80° | 90° | |
| 0° | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 10 | 0.1745 | 0.1745 | 0.1744 | 0.1743 | 0.1742 | 0.1740 | 0.1739 | 0.1738 | 0.1737 | 0.1736 |
| 20 | 0.3491 | 0.3489 | 0.3483 | 0.3473 | 0.3462 | 0.3450 | 0.3438 | 0.3429 | 0.3422 | 0.3420 |
| 30 | 0.5236 | 0.5229 | 0.5209 | 0.5179 | 0.5141 | 0.5100 | 0.5061 | 0.5029 | 0.5007 | 0.5000 |
| 40 | 0.6981 | 0.6966 | 0.6921 | 0.6851 | 0.6763 | 0.6667 | 0.6575 | 0.6497 | 0.6446 | 0.6428 |
| 50 | 0.8727 | 0.8698 | 0.8614 | 0.8483 | 0.8317 | 0.8134 | 0.7954 | 0.7801 | 0.7697 | 0.7660 |
| 60 | 1.0472 | 1.0426 | 1.0290 | 1.0076 | 0.9801 | 0.9493 | 0.9184 | 0.8914 | 0.8728 | 0.8660 |
| 70 | 1.2217 | 1.2149 | 1.1949 | 1.1632 | 1.1221 | 1.0750 | 1.0266 | 0.9830 | 0.9514 | 0.9397 |
| 80 | 1.3963 | 1.3870 | 1.3597 | 1.3161 | 1.2590 | 1.1926 | 1.1225 | 1.0565 | 1.0054 | 0.9848 |
| 90 | 1.5708 | 1.5589 | 1.5238 | 1.4675 | 1.3931 | 1.3055 | 1.2111 | 1.1184 | 1.0401 | 1.0000 |
Повні еліптичні інтеграли


|
Повні еліптичні інтеграли |
||||||||
|
|
|
|
|
|
|
|
|
|
| 0 | 1.5708 | 1.5708 | 30 | 1.6858 | 1.4675 | 60 | 2.1565 | 1.2111 |
| 1 | 1.5709 | 1.5707 | 31 | 1.6941 | 1.4608 | 61 | 2.1842 | 1.2015 |
| 2 | 1.5713 | 1.5703 | 32 | 1.7028 | 1.4539 | 62 | 2.2132 | 1.1920 |
| 3 | 1.5719 | 1.5697 | 33 | 1.7119 | 1.4469 | 63 | 2.2435 | 1.1826 |
| 4 | 1.5727 | 1.5689 | 34 | 1.7214 | 1.4397 | 64 | 2.2754 | 1.1732 |
| 5 | 1.5738 | 1.5678 | 35 | 1.7312 | 1.4323 | 65 | 2.3088 | 1.1638 |
| 6 | 1.5751 | 1.5665 | 36 | 1.7415 | 1.4248 | 66 | 2.3439 | 1.1545 |
| 7 | 1.5767 | 1.5649 | 37 | 1.7522 | 1.4171 | 67 | 2.3809 | 1.1453 |
| 8 | 1.5785 | 1.5632 | 38 | 1.7633 | 1.4092 | 68 | 2.4198 | 1.1362 |
| 9 | 1.5805 | 1.5611 | 39 | 1.7748 | 1.4013 | 69 | 2.4610 | 1.1272 |
| 10 | 1.5828 | 1.5589 | 40 | 1.7868 | 1.3931 | 70 | 2.5046 | 1.1184 |
| 11 | 1.5854 | 1.5564 | 41 | 1.7992 | 1.3849 | 71 | 2.5507 | 1.1096 |
| 12 | 1.5882 | 1.5537 | 42 | 1.8122 | 1.3765 | 72 | 2.5998 | 1.1011 |
| 13 | 1.5913 | 1.5507 | 43 | 1.8256 | 1.3680 | 73 | 2.6521 | 1.0927 |
| 14 | 1.5946 | 1.5476 | 44 | 1.8396 | 1.3594 | 74 | 2.7081 | 1.0844 |
| 15 | 1.5981 | 1.5442 | 45 | 1.8541 | 1.3506 | 75 | 2.7681 | 1.0764 |
| 16 | 1.6020 | 1.5405 | 46 | 1.8691 | 1.3418 | 76 | 2.8327 | 1.0686 |
| 17 | 1.6061 | 1.5367 | 47 | 1.8848 | 1.3329 | 77 | 2.9026 | 1.0611 |
| 18 | 1.6105 | 1.5326 | 48 | 1.9011 | 1.3238 | 78 | 2.9786 | 1.0538 |
| 19 | 1.6151 | 1.5283 | 49 | 1.9180 | 1.3147 | 79 | 3.0617 | 1.0468 |
| 20 | 1.6200 | 1.5238 | 50 | 1.9356 | 1.3055 | 80 | 3.1534 | 1.0401 |
| 21 | 1.6252 | 1.5191 | 51 | 1.9539 | 1.2963 | 81 | 3.2553 | 1.0338 |
| 22 | 1.6307 | 1.5141 | 52 | 1.9729 | 1.2870 | 82 | 3.3699 | 1.0278 |
| 23 | 1.6365 | 1.5090 | 53 | 1.9927 | 1.2776 | 83 | 3.5004 | 1.0223 |
| 24 | 1.6426 | 1.5037 | 54 | 2.0133 | 1.2681 | 84 | 3.6519 | 1.0172 |
| 25 | 1.6490 | 1.4981 | 55 | 2.0347 | 1.2587 | 85 | 3.8317 | 1.0127 |
| 26 | 1.6557 | 1.4924 | 56 | 2.0571 | 1.2492 | 86 | 4.0528 | 1.0086 |
| 27 | 1.6627 | 1.4864 | 57 | 2.0804 | 1.2397 | 87 | 4.3387 | 1.0053 |
| 28 | 1.6701 | 1.4803 | 58 | 2.1047 | 1.2301 | 88 | 4.7427 | 1.0026 |
| 29 | 1.6777 | 1.4740 | 59 | 2.1300 | 1.2206 | 89 | 5.4349 | 1.0008 |
| 30 | 1.6858 | 1.4675 | 60 | 2.1565 | 1.2111 | 90 |
|
1.0000 |