Курсовая работа: Измеримые множества
В теории функций вещественной переменной большую роль играет понятие меры точечного множества, обобщающее понятие длины промежутка, площади прямоугольника, объема параллелепипеда и т.д. В этой главе мы изложим теорию измерения линейных ограниченных точечных множеств, принадлежащую А.Лебегу.
Так как наиболее простой структурой обладают открытые множества, то естественно начать именно с них.
Определение 1. Мерой интервала (a, b) называется его длина, т.е. b - a. Это число обозначается так:
m (a, b) = b - a
Очевидно, что всегда m (a, b) > 0.
Лемма 1. Если в интервале D содержится конечное число взаимно не налегающих интервалов d1, d2, ..., dn, то
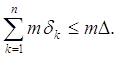
Д о к а з а т е л ь с т в о. Пусть D = (A, B), dk = (ak, bk) (k = 1, 2, …, n).
Не нарушая общности, можно считать, что интервалы dk перенумерованы в порядке возрастания левых концов, т.е. что
a1 < a2 < … < an.
Но тогда, очевидно, bk £ ak+1 (k = 1, 2, …, n - 1), ибо иначе интервалы dk и dk+1 налегали бы друг на друга. Поэтому сумма
Q = (B - bn) + (an - bn-1) + … + (a2 - b1) + (a1 - A)
не отрицательна. Но очевидно, что 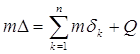
![]() ,
откуда и следует лемма.
,
откуда и следует лемма.
Следствие. Если на интервале D лежит счетное множество взаимно не налегающих интервалов dk (k = 1, 2, 3, …), то
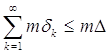 .
.
[Имея дело с положительным расходящимся рядом, мы
приписываем ему сумму, равную + ¥; поэтому всякий положительный ряд имеет
некоторую сумму. Неравенства ![]() k< C (положительного ряда) гарантирует его
сходимость.]
k< C (положительного ряда) гарантирует его
сходимость.]
Определение 2. Мерой mG непустого открытого ограниченного множества G называется сумма длин всех его составляющих интервалов dk:
![]()
(Не зная, конечно или счетно
множество {dk}, мы
будем употреблять обозначение ![]() dk, подразумевая, смотря по
обстоятельствам, под этим символом
dk, подразумевая, смотря по
обстоятельствам, под этим символом ![]()
![]() k или
k или ![]() k.)
k.)
В силу вышеотмеченного следствия,
mG< + ¥
Если множество G пусто, то мы , по определению, полагаем
mG=0,
так что всегда mG³0.
Если D есть интервал, содержащий в себе открытое множество G, то
mG £ mD,
что вытекает из того же следствия.
Пример (Канторово множество G0). Построение Канторова множества G0 состояло из ряда последовательных шагов.
На первом шагу брался![]() интервал (1/3, 2/3) длины
1/3. На втором шагу к нему присоединялись два интервала: (1/9, 2/9) и (7/9,
8/9), длины 1/9 каждый.
интервал (1/3, 2/3) длины
1/3. На втором шагу к нему присоединялись два интервала: (1/9, 2/9) и (7/9,
8/9), длины 1/9 каждый.
На третьем шагу присоединялись еще четыре интервала, длины 1/27 каждый и т.д.
Таким образом
mG0 =![]() …
…![]()
Суммируя по известной формуле эту прогрессию, получаем
mG0 = 1.
Теорема 1. Пусть G1 и G2 два ограниченных открытых множества. Если G1 Ì G2, то
mG1 £ mG2.
Д о к а з а т е л ь с т в о. Пусть di (i = 1, 2, …) и Dk (k = 1, 2, …) суть, соответственно, составляющие интервалы множеств G1 и G2.
В силу теоремы 4, § 5, гл.II, каждый из интервалов di содержится в одном (и только одном) из интервалов Dk.
Поэтому множество {di} можно разбить на ряд взаимно не пересекающихся подмножеств А1, А2, А3,…, относя di в Аk в том случае, когда di Ì Dk.
Тогда, пользуясь известными свойствами двойных рядов, мы можем написать
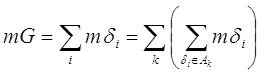 .
.
Но, в силу следствия леммы 1,
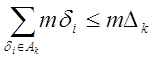 , откуда
, откуда 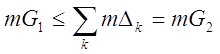 ,
,
что и требовалось доказать.
Следствие. Мера открытого ограниченного множества G есть точная нижняя граница мер всевозможных открытых ограниченных множеств, содержащих G.
Теорема 2. Если открытое ограниченное множество G является суммой конечного числа или счетного множества взаимно не налегающих открытых множеств
![]() ,
,
то
![]() .
.
Это свойство меры называется полной аддитивностью.
Д о к а з а т е л ь с т в о. Пусть ![]() (i = 1, 2, …)
суть составляющие интервалы множества Gk. Покажем, что
каждый из них является составляющим интервалом суммы G.
(i = 1, 2, …)
суть составляющие интервалы множества Gk. Покажем, что
каждый из них является составляющим интервалом суммы G.
В самом деле, то обстоятельство, что ![]() G, очевидно.
Остается убедиться, что концы интервала
G, очевидно.
Остается убедиться, что концы интервала ![]() не
принадлежат G. Допустим, что, например, правый конец интервала
не
принадлежат G. Допустим, что, например, правый конец интервала ![]() принадлежит G.
Тогда этот правый конец (обозначим его через m) должен принадлежать
какому-нибудь из слагаемых множеств. Пусть m Î Gk'. (Очевидно k¢ ¹
k, ибо множеству Gk точка m заведомо не принадлежит.) Но
множество Gk¢ открыто и, стало быть, точка m принадлежит одному из
составляющих интервалов этого множества m Î di¢(k¢).
Однако это влечет
за собой то, что интервалы di(k) и di¢(k¢)
пересекаются,
последнее же противоречит условию Gk Gk¢= 0.
принадлежит G.
Тогда этот правый конец (обозначим его через m) должен принадлежать
какому-нибудь из слагаемых множеств. Пусть m Î Gk'. (Очевидно k¢ ¹
k, ибо множеству Gk точка m заведомо не принадлежит.) Но
множество Gk¢ открыто и, стало быть, точка m принадлежит одному из
составляющих интервалов этого множества m Î di¢(k¢).
Однако это влечет
за собой то, что интервалы di(k) и di¢(k¢)
пересекаются,
последнее же противоречит условию Gk Gk¢= 0.
Итак, действительно, каждый из di(k) есть составляющий интервал множества G. С другой стороны, каждая точка G принадлежит хоть одному di(k) . Наконец, все эти интервалы различны. Таким образом, множество
![]() (i = 1, 2, …; k = 1, 2, …)
(i = 1, 2, …; k = 1, 2, …)
есть множество всех составляющих интервалов суммы G.
Установив это, уже легко закончить доказательство:
![]()
![]() =
=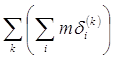
![]()
что и требовалось доказать.
Для того чтобы перенести теорему (соответственно изменить ее) на случай суммы п е р е с е к а ю щ и х с я слагаемых, нам понадобятся две простые леммы.
Лемма 2. Пусть сегмент [P, Q] покрыт конечной системой Н интервалов (l, m ). Тогда
![]()
![]()
Д о к а з а т е л ь с т в о. Выделим
из системы Н некоторую ее часть Н*, которая строится следующим образом:
обозначим через (l1,![]() ) какой-нибудь из интервалов
системы H, содержащих
точку P
) какой-нибудь из интервалов
системы H, содержащих
точку P
l1 < P < m1
(хоть
один такой интервал существует). Если окажется, что m1>Q, то интервал (l1, m1) , и составляет требуемую
систему H* . Если же m1![]() Q, то m1Î[P, Q], и можно в системе H найти интервал ( l2, m2), содержащий точку m1 ,
Q, то m1Î[P, Q], и можно в системе H найти интервал ( l2, m2), содержащий точку m1 ,
l2 < m1 < m2
Если окажется, что m2>Q, то процесс окончен, и интервалы (l1, m1) и ( l2, m2) и составляют систему Н*.
Если же m2![]() Q, то m2Î[P, Q], и можно в системе H найти интервал ( l3, m3), содержащий m2.
Q, то m2Î[P, Q], и можно в системе H найти интервал ( l3, m3), содержащий m2.
l3 < m2 < m3
Если m3>Q, то процесс закончен, а если m3![]() Q, то продолжаем наш процесс.
Q, то продолжаем наш процесс.
Но ведь множество H по условию конечно, а наш процесс состоит в выделении из H все новых и новых интервалов, ибо
m1 < m2 < m3 < …
Поэтому процесс обязательно должен закончится, а конец его состоит в том, что какая-то из точек mk окажется лежащей правее точки Q.
Пусть mn>Q, но mn-1£Q, т.е. процесс заканчивается после n-го шага.
Тогда интервалы (l1, m1), ( l2, m2), … , (ln, mn) и составляют систему H. При этом lk+1<mk (k = 1, 2, … , n-1).
Значит
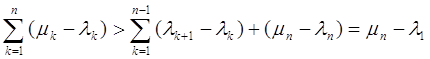
а
так как mn - l1 > Q – P, то Q – P < ![]() , откуда и подавно
, откуда и подавно
Q – P < ![]() .
.
Лемма 3. Пусть интервал D есть сумма конечного или счетного множества открытых множеств
D = ![]() .
.
Тогда
mD![]() .
.
Д о к а з а т е л ь с т в о. Пусть D = (A, B) и пусть составляющие интервалы множества Gk суть di(k) (i = 1, 2, …).
Возьмем положительное число e (0 < e
< ![]() ) и рассмотрим сегмент
) и рассмотрим сегмент ![]() , содержащийся в интервале
D.
, содержащийся в интервале
D.
Этот сегмент покрыт системой интервалов di(k) (i = 1, 2, …; k = 1, 2, …). Применяя к этой системе теорему Бореля о конечном покрытии из § 2, гл. II, мы получим некоторую конечную систему
![]() (s = 1, 2, … n),
(s = 1, 2, … n),
покрывающую сегмент ![]() .
В силу предыдущей леммы,
.
В силу предыдущей леммы, 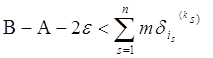 ,
откуда и подавно
,
откуда и подавно
B – A - 2e < 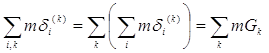 .
.
Так как число e произвольно мало, то
B – A ![]() ,
,
и лемма доказана.
Теорема 3. Если открытое ограниченное
множество G является суммой конечного числа или счетного множества
открытых множеств Gk, G = ![]() , то
, то
mG![]() .
.
Д о к а з а т е л ь с т в о.
Пусть Di (i = 1, 2, …) суть составляющие интервалы суммы G. Тогда mG = ![]() .
.
Но ![]() откуда, в силу леммы 3,
откуда, в силу леммы 3, ![]() и, стало быть,
и, стало быть,
![]() (*)
(*)
С другой стороны ![]()
При этом (что является здесь
основным) отдельные слагаемые правой части взаимно не пересекаются
(потому что ![]() при i¹i`). Значит, мы находимся в
условиях применимости теоремы 2, а потому
при i¹i`). Значит, мы находимся в
условиях применимости теоремы 2, а потому
![]() (**)
(**)
Сопоставляя (*) и (**), мы и получаем теорему.
Мера ограниченного замкнутого множества
Пусть F непустое ограниченное замкнутое множество и S
наименьший сегмент, содержащий множество F. Как известно,
множество CSF открыто и поэтому имеет определенную меру ![]() m[CSF]. Это дает возможность установить следующее
определение.
m[CSF]. Это дает возможность установить следующее
определение.
Определение 1. Мерой непустого ограниченного замкнутого множества F называется число
![]()
где S=[A, B] есть наименьший сегмент, содержащий множество F.
Для пустого замкнутого множества меру определять не нужно, ибо такое множество открыто и мерой его мы уже условились считать число 0. Кроме того, непустое замкнутое ограниченное множество не может оказаться открытым множеством, так что нет надобности ставить вопрос о связи определений меры открытого и замкнутого множества.
Рассмотрим некоторые примеры.
1. F=[a, b]. В этом случае, очевидно, S=[a, b] и CsF=0, так, что m [a, b] = b – a, т. е. мера сегмента равна его длине.
2. F есть сумма конечного числа попарно не пересекающихся
сегментов ![]()
Можно считать, что сегменты перенумерованы в порядке возрастания левых концов; тогда, очевидно,
![]() (k=1, 2, … n-1),
(k=1, 2, … n-1),
откуда следует, что
![]()
![]()
Стало быть,
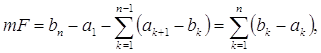
т.е. мера суммы конечного числа попарно не пересекающихся сегментов равна сумме длин этих сегментов.
3. Пусть ![]()
![]() (Канторово совершенное множество). В этом случае
(Канторово совершенное множество). В этом случае
![]() и
и ![]() откуда
откуда
![]()
т.е.
Канторово совершенное множество ![]() имеет
меру нуль. Этот факт интересно сопоставить с тем, что мощность множества
имеет
меру нуль. Этот факт интересно сопоставить с тем, что мощность множества ![]() есть с.
есть с.
Теорема 1. Мера ограниченного замкнутого множества F не отрицательна.
Д о к а з а т е л ь с т в о. Действительно, если
пользоваться обозначениями определения 1, то очевидно ![]() Ì (А, В), и по теореме 1,
Ì (А, В), и по теореме 1, ![]() откуда и следует, что
откуда и следует, что ![]()
Лемма. Пусть F ограниченное замкнутое множество, содержащееся в интервале D, тогда
![]() D- [ CDF]
D- [ CDF]
Д о к а з а т е л ь с т в о. Множество CDF – открыто, так что лемма имеет смысл. Пусть D=(A, B), а наименьший сегмент, содержащий множество F, есть S=[a, b] (рис.1.).
Тогда легко видеть, что СDF=CDS+CsF.
Рис. 1
Оба слагаемые правой части открыты и взаимно не налегают. Значит, по свойству аддитивности меры (теорема 2) будет m[CDF]=m[CDS]+m[CsF].
Но, очевидно,CDS = (A, a) + (b, B), откуда
m[CD] = (a-A) + (B-b),
и следовательно,
m[CDF]=(B-A)-(b-a)+m[CsF],
что и доказывает лемму.
Теорема 2. Пусть F1 и F2 два ограниченных замкнутых множества. Если F1Ì F2, то mF1£ mF2.
Д о к а з а т е л ь с т в о. Пусть D есть интервал, содержащий множество F2. Тогда легко
проверить, что СDF1 É CDF2,
и, стало быть, m[CDF1 ] ![]() [ CDF2 ], так что дело
сводиться к предыдущей лемме.
[ CDF2 ], так что дело
сводиться к предыдущей лемме.
Следствие. Мера ограниченного замкнутого множества F есть точная верхняя граница мер всевозможных замкнутых множеств, содержащихся в F.
Теорема 3. Пусть F замкнутое множество, а G открытое ограниченное
множество. Если FÌ G, то mF![]() mG.
mG.
Д о к а з а т е л ь с т в о.
Пусть D есть
интервал, содержащий множество G. Легко видеть, что D= G+CDF, откуда, в силу теоремы 3,
получаем, что mD![]() mG + m[CDF], и дело сводится к лемме.
mG + m[CDF], и дело сводится к лемме.
Теорема 4. Мера открытого ограниченного множества G есть точная верхняя граница мер всевозможных замкнутых множеств, содержащихся в G.
Д о к а з а т е л ь с т в о. В силу предыдущей теоремы, mG есть точная граница мер замкнутых множеств FÌG, и надо доказать, что меры этих замкнутых множеств могут быть сколь угодно близки к mG.
Пусть составляющие интервалы
множеств G суть(lk, mk ) (k=1, 2, …), так что mG = ![]() (mk - lk).
(mk - lk).
Возьмем произвольное e > 0 и найдем столь большое натуральное n, чтобы оказалось 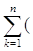 mk - lk)> mG -
mk - lk)> mG - 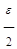 .
.
[ak bk,] Ì (lk, mk), m[ak, bk] > m(lk, mk) -![]() ,
,
(для чего достаточно взять такое hk, что
0 < hk < min[![]() ,
, ![]() ]
]
и положить ak = lk+hk, bk =mk - hk). Положим, наконец,
F0= ![]() k, bk].
k, bk].
Тогда, очевидно, F0 Ì G, F0 замкнуто и
mF0=![]() (bk-ak) >
(bk-ak) > ![]() (mk-lk) -
(mk-lk) - ![]() > mG - e.
> mG - e.
Так как e произвольно мало, то теорема доказана.
Теорема 5. Мера замкнутого ограниченного множества F есть точная нижняя граница мер всевозможных открытых ограниченных множеств, содержащих F.
Д о к а з а т е л ь с т в о. Как и выше, достаточно показать, что можно построить открытое ограниченное множество, содержащее множество F и имеющее меру, сколь угодно близкую к mF.
С этой целью возьмем интервал D, содержащий множество F, и рассмотрим открытое множество CDF. Каково бы ни было e>0, мы можем (в силу теоремы 4) найти замкнутое множество Ф такое, что Ф Ì СDF, mФ>m[CDF] - e.
Положим G0 = СDФ. Легко видеть, что G0 есть открытое множество, содержащее F. Вместе с тем
mG0 = mD - mФ < mD - m[CDF] + e = mF + e![]()
Теорема доказана.
Теорема 6 . Пусть ограниченное замкнутое множество F есть сумма конечного числа взаимно не пересекающихся замкнутых множеств
F = 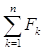 (FkFk’
= 0, k ¹ k’).
(FkFk’
= 0, k ¹ k’).
mF = 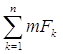
Д о к а з а т е л ь с т в о. Очевидно, достаточно рассмотреть случай двух слагаемых F = F1+F2 (F1F2=0).
Возьмем произвольное e > 0 и подберем два ограниченных открытых множества G1 и G2 так, чтобы оказалось
Gi É Fi ![]() (i = 1, 2),
(i = 1, 2),
что возможно в силу предыдущей теоремы.
Положим G = G1 + G2.
Тогда G есть открытое ограниченное множество, содержащее множество F. Значит,
mF £ mG £ mG1 + mG2 < mF1 + mF2 + e.
В силу произвольности e, отсюда следует что
mF £ mF1 + mF2 (*)
С другой стороны, в силу теоремы отделимости, существуют такие открытые множества B1 и B2, что
Bi É Fi (i = 1, 2), B1B2 = 0.
Отметив это возьмем произвольное e > 0 и найдем такое открытое ограниченное множество G, что G É F, mG < mF + e.
Тогда множества B1G и B2G суть открытые ограниченные взаимно не пересекающиеся множества, содержащие, соответственно, множества F1 и F2.
Значит,
MF1 + mF2 £ m(B1G) + m(B2G) = m [B1G + B2G]
(здесь мы воспользовались аддитивностью меры для открытых множеств). Но B1G + B2G Ì G, откуда
mF1+mF2 £ mG < mF+e
и в силу произвольности e,
mF1 + mF2 £ mF. (**)
Сопоставляя (*) и (**), получим
mF = mF1 + mF2,
что и требовалось доказать.
Внешняя и внутренняя меры ограниченного множества
Определение 1. Внешней мерой m*E ограниченного множества E называется точная нижняя граница мер всевозможных открытых ограниченных множеств, содержащих множество E:
![]()
Очевидно, для всякого ограниченного множества E cуществует внешняя мера, причем 0 £ m*E < +¥.
Определение 2. Внутренней мерой m*E ограниченного множества E называется точная верхняя
граница мер всевозможных замкнутых множеств, содержащихся в множестве E:![]()
m*E=![]() .
.
Очевидно, что всякое ограниченное множество E имеет внутреннюю меру, причем 0 £ m*E < +¥.
Теорема 1. Если G есть открытое ограниченное множество, то
m*G = m*G = mG.
Теорема вытекает из следствия теоремы 1 и теоремы 4.
Теорема 2. Если F есть замкнутое ограниченное множество, то
m*F = m*F = mF.
Теорема вытекает из следствия теоремы 2 и теоремы 5.
Теорема 3. Для всякого ограниченного множества Е
m*E £ m*E.
Д о к а з а т е л ь с т в о. Пусть G ограниченное открытое множество, содержащее множество Е. Какое бы замкнутое подмножество F множества Е ни взять, будет F Ì G и, в силу теоремы 3, mF £ mG. Отсюда m*E £ mG. Но так как это верно для всякого открытого ограниченного множества G, содержащего Е, то m*E £ m*E, что и требовалось доказать.
Теорема 4. Пусть A и B суть ограниченные множества. Если A Ì В, то
m*A £ m*В, m*A £ m*B.
Д о к а з а т е л ь с т в о. Оба неравенства доказываются аналогично. Остановимся для примера на первом из них.
Пусть S есть множество, состоящее из мер всевозможных замкнутых подмножеств множества А, а Т такое же множество для множества В. Тогда m*A = sup S, m*B = sup T.
Пусть F есть замкнутое подмножество А, тогда и подавно F является подмножеством множества В. Отсюда следует, что S Ì T, и теорема вытекает из того известного факта, что точная верхняя граница подмножества какого-либо множества не превосходит точной верхней границы самого этого множества.
Теорема 5. Если ограниченное множество Е есть сумма конечного числа или счетного множества множеств Еk
E=![]() , то m*E£
, то m*E£![]() .
.![]()
Д о к а з а т е л ь с т в о.
Теорема тривиальна в случае расходимости ряда ![]() .
Предположим, что этот ряд сходится. Взяв произвольное e > 0, мы можем найти такие
открытые ограниченные множества Gk, что
.
Предположим, что этот ряд сходится. Взяв произвольное e > 0, мы можем найти такие
открытые ограниченные множества Gk, что
GkÉEk, mGk<m*Ek+![]() (R=1, 2, 3, …).
(R=1, 2, 3, …).
Назовем через D какой-нибудь интервал,
содержащий множество Е. Тогда ЕÌD![]() , откуда, в силу теоремы 3.
, откуда, в силу теоремы 3.
m*E £ m![]() = m
= m![]()
![]() £
£ ![]() ,
,
и теорема вытекает из произвольности числа e.
Теорема 6. Если ограниченное множество Е есть сумма конечного числа или счетного множества взаимно не налегающих множеств Еk
Е=![]() (EkEk’=0, k¹k’),
(EkEk’=0, k¹k’),
то
m*E³![]() *Ek.
*Ek.
Д о к а з а т е л ь с т в о. Рассмотрим первые n множеств Е1, Е2,... …, Еn. Для любого e > 0 существуют такие замкнутые множества Fk, что
FkÌEk, mFk>m*Ek-![]() (k=1, 2, …, n).
(k=1, 2, …, n).
Множества Fk попарно не пересекаются и сумма их  замкнута. Отсюда, применяя
теорему 6, получим
замкнута. Отсюда, применяя
теорему 6, получим
m*E ³ m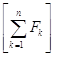 =
= ![]() mFk >
mFk > ![]() m*Ek - e.
m*Ek - e.
Так как e > 0 произвольно, то ![]() m*Ek £ m*E.
m*Ek £ m*E.
Этим теорема доказана для случая
конечного числа слагаемых множеств. Если же этих множеств имеется счетное
множество, то, опираясь на произвольность числа n, мы установим сходимость ряда ![]() m*Ek и неравенство
m*Ek и неравенство ![]() m*Ek £ m*E.
m*Ek £ m*E.
Легко видеть, что теорема перестает быть справедливой, если отбросить условие отсутствия общих точек у множеств Ek. Например, если Е1=[0, 1], Е2=[0, 1] Е=Е1+Е2, то m*E=1, m*E1+m*E2=2.
Теорема 7. Пусть Е ограниченное множество. Если D интервал, содержаций это множество, то
m* E+m*[CDE]=mD.
Д о к а з а т е л ь с т в о. Возьмем произвольное e>0 и найдем такое замкнутое множество F, что FÌCDЕ, mF>m*[CDE]- e.
Если мы положим G=CDF, то множество G будет открытым ограниченным множеством, содержащим множество Е, откуда, с помощью леммы находим
m*E £ mG = mD - mF < mD - m*[CDE] + e.
Отсюда, в силу произвольности e, следует, что
m*E + m*[CDE] £ mD.
Для того чтобы получить обратное неравенство
m*E + m*[CDE] ³ mD, (*)
приходится рассуждать тоньше.
Возьмем e>0
и найдем такое открытое ограниченное множество G0,
что G0
É Е, mG0 < m*E + 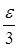 .
.
Назовем концы интервала D через A и B и построим такой содержащийся в D интервал (a, b), что
A < a < A+![]() , В -
, В - ![]() < b < B.
< b < B.
Сделав это, положим G = DG0 + (A, a) + (b, B).
Множество G открыто, ограничено, содержит E и таково, что
mG < m*E + e.
Но кроме того (и это здесь основное) множество F = CDG оказывается замкнутым, что вытекает из легко проверяемого тождества F = [а, b] × CG.
Так как F Ì СDЕ, то m*[СDЕ] ³ mF = mD - mG > mD - m*E -e.
Отсюда, в силу произвольности e, следует неравенство (*), а с ним и теорема.
Следствие. В обозначениях теоремы будет
m*[CDЕ] - m*[CDЕ] = m*E – m*E.
В самом деле, если мы переменим роли множеств Е и СDЕ, то получим, что m*[CDЕ] + m*Е = mD, откуда
m*[CDЕ] + m*E = m*E + m*[CDE],
а это равносильно доказываемому утверждению.
Измеримые множества
Определение. Ограниченные множество Е называется измеримым, если его внешняя и внутренняя меры равны друг другу :
m*E=m*E.
Их общее значение называется мерой множества E и обозначается через mE:
mE=m*E=m*E .
Этот способ определения понятия меры принадлежит Лебегу, в связи с чем иногда измеримое множество называют множеством “измеримым в смысле Лебега”, или, короче, “измеримым (L)”.
Если множество E неизмеримо, то о его мере нельзя говорить, и символ mE для нас лишен смысла. В частности, неизмеримыми мы считаем все неограниченные множества.
Теорема 1. Открытое ограниченное множество измеримо и его вновь определенная мера совпадает с мерой.
Этот результат есть непосредственное следствие теоремы 1. Точно также из теоремы 2, вытекает следующая теорема:
Теорема 2. Замкнутое ограниченное множество измеримо и его вновь определенная мера совпадает с введенной.
Из следствия теоремы 7, вытекает:
Теорема 3. Если Е есть ограниченное множество, содержащееся в интервале D, множества Е и СDЕ одновременно измеримы или нет.
Из сопоставления теорем 5 и 6 предыдущей темы следует:
Теорема 4. Если ограниченное множество Е есть сумма конечного числа или счетного множества измеримых множеств, попарно не имеющих точек,
![]() (ЕkЕk’ = 0, k ¹ k’),
(ЕkЕk’ = 0, k ¹ k’),
то множество Е измеримо и
![]()
Д о к а з а т е л ь с т в о вытекает из следующей цепи неравенств:
![]()
Доказанное свойство меры называется ее полной аддитивностью.
В последней теореме существенно было, что отдельные слагаемые попарно не пересекаются. Избавимся от этого ограничения, пока, впрочем, для случая конечного числа слагаемых множеств.
Теорема 5. Сумма конечного числа измеримых множеств есть измеримое множество.
Д о к о з а т е л ь с т в о.
Пусть 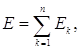 причем множества
причем множества
Ek (k =1, 2, …, n) измеримы.
Возьмем произвольное e>0 и построим для каждого k такое замкнутое множество Fk и такое открытое ограниченное множество Gk, чтобы было
Fk Ì Ek Ì Gk, mGk – mFk <![]() (k = 1, 2, …, n).
(k = 1, 2, …, n).
Сделав это, положим 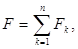

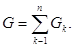
Очевидно, что множество F замкнуто, а G открыто и ограничено, и что
F Ì E Ì G, откуда следует, что
mF £ m*E £ m* E £ mG. (*)
Но множество G – F открыто (ибо его можно представить в форме
G · CF) и ограничено. Значит, это множество измеримо. Множество F также измеримо, а потому, поскольку
G = F + (G – F)
и множества F и G – F не пересекаются, можно применить предыдущую теорему, что дает mG = mF + m(G – F), откуда
m(G – F) = mG – mF.
Аналогично мы установим, что
m(Gk – Fk) = mGk – mFk (k = 1, 2, …, n).
Отметим теперь легко проверяемое включение
G-F![]() (Gk-Fk).
(Gk-Fk).
Все входящие сюда множества открыты и ограничены, так что, на основании теорем § 1, мы имеем
m(G-F)![]()
или
mG - mF![]() <e.
<e.![]()
Отсюда и из (*) вытекает, что m*E - m*E<e, а также как e сколь угодно мало, то
m*E = m*E.
Теорема 6. Пересечение конечного числа измеримых множеств измеримо.
Д о к а з а т е л ь с т в о.
Пусть E=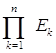 , причем множества Ek измеримы. Назовем через D какой-нибудь интервал,
содержащий все множества Ek. Легко проверить, что CDE=
, причем множества Ek измеримы. Назовем через D какой-нибудь интервал,
содержащий все множества Ek. Легко проверить, что CDE=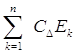 .
.
Но множества С![]() Ek измеримы одновременно с
множествами Ek, откуда, в силу теоремы 5, следует измеримость множества CDE, а с ним и множества E, что и требовалось доказать.
Ek измеримы одновременно с
множествами Ek, откуда, в силу теоремы 5, следует измеримость множества CDE, а с ним и множества E, что и требовалось доказать.
Теорема 7. Разность двух измеримых множеств измерима.
Д о к а з а т е л ь с т в о. Пусть E = E1 - E2, где множества E1 и E2 измеримы. Назовем через D какой-нибудь интервал, содержащий оба множества E1 и E2. Тогда E=E1·CDE2 и дело сводится к предыдущей теореме.
Теорема 8. Если в условиях теоремы 7 будет
E1 ![]() E2, то
E2, то
ME = mE1 - mE2.
Д о к а з а т е л ь с т в о. Очевидно E1=E+E2 (EE2=0), откуда, в силу теоремы 4, mE1=mE+mE2, что равносильно теореме.
Теорема 9. Если ограниченное множество E является суммой счетного множества измеримых множеств, то E измеримо.
Д о к а з а т е л ь с т в о.
Пусть E=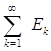 .
.
Введем множества Ak (k=1, 2, …), полагая
A1=E1, A2=E2-E1, …, Ak=Ek-(E1+…+Ek-1), …
Легко проверить, что ![]() .
При этом все множества Ak измеримы
и попарно не пересекаются (в последнем вся суть доказательства), так что дело
свелось к теореме 4.
.
При этом все множества Ak измеримы
и попарно не пересекаются (в последнем вся суть доказательства), так что дело
свелось к теореме 4.
Условие ограниченности множества Е (которое в теореме
5 выполнялось само собой) отбросить нельзя, как видно хотя бы из примера Еk = [0, k],
где сумма ![]() k = [0, +
k = [0, +![]() ) неизмерима.
) неизмерима.
Теорема 10. Пересечение счетного множества измеримых множеств измеримо.
Д о к а з а т е л ь с т в о. Пусть 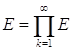 k,
где все множества Еk измеримы. Так как Е
k,
где все множества Еk измеримы. Так как Е![]() Е1,
то множество Е ограничено. Обозначим через D какой-нибудь
интервал, содержащий это множество, и положим Аk= D Еk (k=1,
2, 3, …).
Е1,
то множество Е ограничено. Обозначим через D какой-нибудь
интервал, содержащий это множество, и положим Аk= D Еk (k=1,
2, 3, …).
Тогда
![]() k=
k=![]() k)=
k)=![]() k.
k.
Легко проверить, что ![]() , и дело сводится к
теоремам 3 и 9.
, и дело сводится к
теоремам 3 и 9.
В заключение установим две теоремы, играющие важную роль в теории функций.
Теорема 11. Пусть множества Е1, Е2, Е3, … измеримы. Если
![]()
и
если сумма 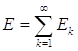 ограничена, то
ограничена, то
![]() [mEn].
[mEn].
Д о к а з а т е л ь с т в о. Легко видеть, что множество Е можно представить в форме
Е=Е1 + (Е2 – Е1) + (Е3 – Е2) + (Е4 – Е3) + …,
где
отдельные слагаемые попарно не пересекаются. Отсюда, в силу теорем 4 и 8,
следует, что![]()
![]()
На основании самого определения суммы бесконечного ряда, последнее равенство можно переписать так
![]() {
{![]()
а это равносильно теореме, ибо
mE1+![]() =mEn
=mEn
Теорема 12. Пусть
E1, E2,E3,…
суть измеримые множества, и Е= ![]() . Если Е1ÉE2ÉE3É…, то
. Если Е1ÉE2ÉE3É…, то
mE=lim![]() .
.
Д о к а з а т е л ь с т в о . Эту теорему легко свести к предыдущей. Действительно, обозначив через D какой-нибудь интервал, содержащий множество Е1, мы будем иметь
СDE1ÌCDE2ÌCDE3Ì ...,
CDE=![]() .
.
В силу теоремы 11 мы получаем, что
m(СDE)=![]()
что можно представить и так:
mD - mE=![]()
а это равносильно теореме.
Измеримость и мера как инварианты движения
Пусть даны два множества А и В, состоящие из объектов любой природы. Если указано правило, которое каждому элементу а множества А ставит в соответствие один и только один элемент b множества В, то говорят, что установлено однозначное отображение множества А в множество В. При этом не предполагается, что каждый элемент множества В оказывается соотнесенным какому-нибудь элементу из А. Понятие отображения есть прямое обобщение понятия функции. В связи с этим элемент b Î В, отвечающий элементу а Î A, часто обозначают через f(а) и пишут b=f (а).
Если b=f(а), то мы будем называть элемент b образом элемента а, а элемент а прообразом элемента b. При этом один элемент b может иметь несколько прообразов.
Пусть А* есть часть множества А, а В* есть множество образов всех элементов А* (иначе говоря, если аÎА*, то f(а) ÎВ*, и если bÎВ*, то существует хоть один элемент аÎА* такой, что f(а) = b). В таком случае множество В* называется образом множества А*, что записывают так: В*= f(А*).
При этом множество А* называется
прообразом множества В*.![]()
Установив эти общие понятия, перейдем к рассмотрению
одного важного специального вида отображений.![]()
Определение 1. Однозначное отображение j (х) числовой прямой Z в себя называется движением, если расстояние между образами любых двух точек прямой равно расстоянию между самими этими точками:
½j (х) - j (y)½= ½ х – y ½.
Иначе говоря, движением называется такое отображение множества Z в множество Z, которое не изменяет расстояний между точками Z.
В определение понятия движения не включено требование, чтобы каждая точка Z cлужила образом какой-нибудь точки, а также требование, чтобы разные точки Z имели разные же образы. Однако оба эти обстоятельства имеют место. Убедимся в этом пока для одного из них.
Теорема 1. Пусть j ( х) есть движение. Если х ¹ y, то j ( х) ¹ j (y).
Действительно, в этом случае ½j (х) - j (y) ½ = ½х - y½¹ 0.
Теорема 2. a) Если А Ì В, то j (А) Ì j ( В).
b) 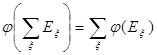
c) 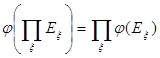
d) Если L пустое множество, то j(L) = L
Доказательство предоставляется читателю; укажем лишь на то, что при доказательстве с) используется теорема 1.
Легко проверить, что следующие три отображения являются движениями:
I. j (х) = х + d (сдвиг),
II. j (х) = - х (зеркальное отражение),
III. j (х) = - х + d.
Чрезвычайно важным является то, что этими тремя (собственно – двумя, ибо III охватывает II) типами исчерпываются все возможные движения в Z.
Теорема 3. Если j (х) есть движение, то либо
j (х) = х + d,
либо
j (х) = - х + d.
Д о к а з а т е л ь с т в о . Положим, j (0) = d. Тогда для всякого х будет | j (х) – d | = | х | и, стало быть,
j ( х ) = (-1) s( х ) х + d [s(х) = 0, 1].
Функция s (х) определена для всякого х ¹ 0. Нашей задачей является установление того, что s (х) есть постоянная величина.
Пусть x и y две точки, причем x ¹ 0, y ¹ 0, x ¹ y. Тогда
j (x) - j (y) = (-1) s (x) x – (-1) s (y) y,
или
j (x) - j (y) = (-1) s (x) [x – (-1) r y],
где r = s (y) - s (x) имеет одно из трех значений r = 1, 0, -1.
Пользуясь определением движения, можно утверждать, что
| x – (-1) r y| = | x - y|.
Отсюда, либо x – (-1)r y = x – y, либо же x – (-1)r y = -x + y.
Но второй случай невозможен, ибо он приводит к тому, что
2x = y [1 + (-1) r ], откуда (при r = ± 1) x = 0, или (при r = 0) x = y, а это противоречит условию.
Значит, остается первый случай, который дает, что r = 0, т.е. s(x) = s(y).
Значит, для всех x ¹ 0 функция s (x) имеет одно и то же значение
s (x) = s (s = 0, 1), так что j (x) = (-1) s x + d.
Поскольку это равенство, очевидно, остается в силе и для x = 0, теорема доказана.
Следствие. При движении каждая точка y Î Z служит образом некоторой точки x Î Z, т.е. j (Z) = Z.
Действительно, если j (x) = (-1) s x + d, то прообразом точки y служит точка x = (-1) s (y-d).
Если j (x) = (-1) s x + d есть некоторое движение, то движение
j-1 (x) = (-1) s (x – d)
называется обратным движением. Эти два движения связаны соотношениями
j [j-1 (x)] = j-1[j (x)] = x.
Иначе говоря, если точка х в движении j имеет образом точку y, то в движении j-1 точка y имеет образом точку х. Весьма важным является то, что для всякого движения существует обратное ему движение.
Теорема 4. При движении: а) всякий интервал переходит в интервал той же меры, причем концами интервала-образа служат образы концов интервала-прообраза;
b) образ ограниченного множества есть ограниченное же множество.
Д о к а з а т е л ь с т в о. Пусть D = (a, b) есть некоторый интервал. Тогда при движении j (x) = x + d образом интервала D служит интервал (а+ d, b + d), а при движении j (x) = -x + d – интервал (d – b, d – a). В обоих случаях mj (D) = b – a = mD.
Чтобы доказать b), обозначим через Е какое-нибудь ограниченное множество. Если D есть интервал, содержащий множество Е, то
j (Е) Ì j (D), так что j (Е) ограничено. Можно рассуждать и так: если для всех х из Е будет | х | < k, то для всех у из j(E) будет | у|<k+|d|.
Теорема 5. При движении: а) замкнутое множество переходит в замкнутое множество;
b) открытое множество переходит в открытое множество.
Д о к а з а т е л ь с т в о. a) пусть j (F) есть образ замкнутого множества F. Обозначим через у0 какую-либо предельную точку множества j (F) и найдем последовательность {уn}, для которой
lim уn = у0 , уn Î j(F).
Пусть х0=j-1(у0), хn= у –1(уn).
Тогда хnÎF. Но | хn – х0 | = | уn – у0 |, так что хn ® х0 и, в силу замкнутости F, х0 Î F, откуда у0 = j (х0) Î j (F).
Значит j(F) есть открытое множество.
b) Пусть G есть открытое множество. Положим F=CG. Тогда F есть замкнутое множество и G+F=Z, G ·F=0.
Отсюда, в силу теоремы 2 и следствия теоремы 3,
j (G) + j (F) = Z, j (G) j ·(F) = 0,
т.е. j (G) является дополнением замкнутого множества j (F) и, стало быть, открыто.
Теорема 6. Мера открытого ограниченного множества не меняется при движении.
Д о к а з а т е л ь с т в о. Пусть
G открытое ограниченное
множество. Тогда и j(G) есть открытое ограниченное множество. Обозначим через dk(k = 1, 2, 3…) составляющие интервалы множества G. На основании теоремы 4,
составляющими интервалами множества j(G) служат интервалы j(dk), причем легко проверить, что
этими интервалами исчерпываются все составляющие интервалы множества j(G). Отсюда: mj(G)=![]() j(dk)=
j(dk)=![]() dk = mG, что и требовалось
доказать.
dk = mG, что и требовалось
доказать.
Теорема 7. Движение не изменяет ни внешней, ни внутренней меры ограниченного множества.
Д о к а з а т е л ь с т в о. а) Пусть E ограниченное множество. Взяв произвольное e>0, найдем такое открытое ограниченное множество G, чтобы было GÉE, mG < m* E + e.
В таком случае j(G) есть открытое ограниченное множество, содержащее множество j(E). Стало быть
m*j(E) £mj(G)=mG < m*E+e.
В силу произвольности числа e, следует, что m*j(E) £m* E, так что при движении внешняя мера ограниченного множества не увеличивается. Но тогда она и не уменьшается, ибо иначе обратное движение привело бы к увеличению внешней меры.
Итак
m*j(E)=m*E.
b) Обозначим через D какой-нибудь интервал, содержащий множество Е. Тогда j (D) есть интервал, содержащий множество j (Е). Положим, далее, А=СD E.
Соотношения Е+А=D, ЕА=0 дают, что
j (E)+j (А)= j ( D), j (Е) · j (А)=0,
так что j (Е) есть дополнительные множества j (А) относительно интервала j (D).Отсюда, в силу теоремы 7,
m* j (А)+m * j (Е)=mj (D)
и, на основании уже доказанной части теоремы и теоремы 4,
m* А+m* j (Е)=mD.
Значит m*j (Е)=mD-m* (CDЕ), и снова применяя теорему 7, мы находим, что
m*j (Е)=m* Е.
Следствие. При движении измеримое множество переходит в измеримое множество той же меры.
Определение 2. Множества А и В называются конгруэнтными, если существует движение, в котором одно из них переходит в другое.
С помощью этого термина доказанные результаты можно высказать в такой форме.
Теорема 8. Конгруэнтные множества имеют одинаковые внешнюю и внутреннюю меры. Множество, конгруэнтное измеримому множеству, измеримо и имеет ту же меру.
Класс измеримых множеств.
Мы изучали свойства самых измеримых множеств, здесь же мы остановимся на некоторых свойствах всего класса измеримых множеств.
Теорема 1. Всякое ограниченное счетное множество измеримо и мера его равна нулю.
Д о к а з а т е л ь с т в о . Пусть ограниченное множество Е состоит из точек х1, х2, х3, …
Обозначим через Еk одноэлементное множество,
состоящее из точки хk. Очевидно
Еk есть измеримое множество меры нуль, и теорема следует
из равенства 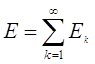 и теоремы 4.
и теоремы 4.
Как показывает пример канторова совершенного множества Р0, доказанная теорема не допускает обращения.
Определение 1. Если множество Е представимо в форме суммы счетного множества замкнутых множеств

то говорят, что Е есть множество типа Fs.
Определение 2. Если множество Е представимо в форме пересечения счетного множества открытых множеств
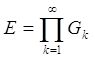 ,
,
то говорят, что Е есть множество типа Gd.
Из теорем 9 и 10 следует
Теорема 2. Всякое ограниченное множество типа Fs или Gd измеримо.
Д о к а з а т е л ь с т в о. Относительно множества типа Fs это очевидно, ибо из ограниченности суммы множеств вытекает ограниченность слагаемых, а так как последние замкнуты, то и измеримы.
Если Е есть ограниченное
множество типа Gd,
то обозначив через D какой-нибудь
интервал, содержащий множество Е, мы сможем представить Е в форме пересечения
измеримых множеств 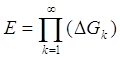 , после чего
измеримость множества Е становится очевидной.
, после чего
измеримость множества Е становится очевидной.
Определение 3. Если множество Е может быть получено, исходя из замкнутых и открытых множеств, с помощью применения конечного числа или счетного множества операций сложения и пересечения, то множество Е называется борелевым множеством. Ограниченное борелево множество называется измеримым (В).
Например, множества типа Fs и типа Gd суть борелевы множества.
Рассуждая как при доказательстве теоремы 2, установим, что верна следующая теорема.
Теорема 3. Множество, измеримое (В), измеримо (L).
Обратная теорема неверна: существуют примеры множеств измеримых (L) и неизмеримых (В). Первый эффективный пример такого множества был построен безвременно умершим московским математиком М.Я. Суслиным (1894-1919). Суслин открыл чрезвычайно важный и обширный класс так называемых А-множеств, каждое из которых (при условии ограниченности) измеримо (L). Этот класс содержит в себе класс всех борелевых множеств, но существенно шире его.
Интересно выяснить, существуют ли вообще ограниченные множества неизмеримые (L)? Прямым счетом этого вопроса решить нельзя, как показывает следующая теорема.
Теорема 4. Множество М всех измеримых множеств имеет ту же можность, что и множество всех точечных множеств, т.е. 2с.
Д о к а з а т е л ь с т в
о. Прежде всего ясно, что 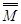
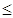 2с.
2с.
С другой стороны, возьмем
какое-либо измеримое множество Е меры нуль и мощности с (например канторово
множество Р0) и обозначим через S множество
всех его подмножеств. Так как всякая часть множества меры нуль также имеет
внешнюю меру нуль и, стало быть, измерима, то SÌM, а
поскольку 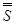 = 2с, то ясно,
что
= 2с, то ясно,
что 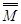
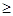 2с.
2с.
Теорема доказана.
Тем не менее, имеет место следующая теорема.
Теорема 5. Существуют ограниченные неизмеримые множества.
Для доказательства этого факта приведем следующий пример.
Пример неизмеримого множества. Разобьем все точки сегмента [-1/2, +1/2] на классы, относятся две точки x и у в один класс, тогда и только тогда, когда разность их х - у есть число рациональное. Это можно сделать следующим образом: соотнесем каждой точке хÎ[-1/2, +1/2] класс K (х), состоящий из тех точек сегмента [-1/2, +1/2], которые имеют вид х + r, где r-рациональное число. В частности х Î K(х).
Покажем, что р а з л и ч н ы е классы K(х) и K(у) не пересекаются между собою. Действительно, предположим, что они пересекаются и пусть zÎK(х)K(у). Тогда z =х + rх=у + rу, где rх и rу рациональные числа, откуда
у = х + rх - rу, где rx и rу рациональные числа, откуда у = x + rx - rу.
Теперь, если t Î K(у), то
t = у + r = x + (rx - rу + r) = x + r’,
так что tÎK(x) и K(у) Ì K(x). Аналогично мы установим, что K(x) Ì K(у) и тогда окажется, что K(x) = K(у), т.е. K(x) и K(у) представляют собою один и тот же класс, вопреки предположению, что это различные классы.
Множество всех построенных таким образом классов и дает нам требуемое разбиение.
Сделав это, выберем из каждого класса по одной точке и обозначим через А множество выбранных точек.
Множество А неизмеримо.
Чтобы доказать это, перенумеруем все рациональные точки сегмента [-1, +1]:
rо = 0, r1, r2, r3, …
и обозначим через Аk множество, получаемое из множества А сдвигом
jk (x) = x + rk.
(Иначе говоря, если x Î A, то x + rkÎ Ak, и если x Î Ak, то x - rk Î A).
В частности, А0 = A. Все множества Аk конгруэнтны друг с другом, а потому (теорема 8)
m*Ak = m*A = a, m*Ak = m*A = b (k = 0, 1, 2, …).
Убедимся, что
b > 0. (1)
Для этого заметим, что
[-![]() , +
, +![]() ]
]![]()
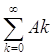 .
(2)
.
(2)
Действительно, если х Î [- ![]() , +
, +![]() ], то х попадает в один из
классов произведенного выше разбиения. Если представитель этого класса в множестве
A есть х0, то разность
х - х 0 есть число рациональное и притом, очевидно, принадлежащее
сегменту [-1, +1], откуда х - х 0 = rk и х Î Ak. Итак, (2) доказано.
], то х попадает в один из
классов произведенного выше разбиения. Если представитель этого класса в множестве
A есть х0, то разность
х - х 0 есть число рациональное и притом, очевидно, принадлежащее
сегменту [-1, +1], откуда х - х 0 = rk и х Î Ak. Итак, (2) доказано.
Но тогда (теорема 5):
1=m*[-![]() , +
, +![]() ] £ m*[
] £ m*[![]() ] £
] £ 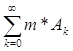 ,
,
т. е.
1£b + b + b + ...,
откуда следует (1).
С другой стороны, легко показать, что
a=0. (3)
Для этого прежде всего убедимся, что при n ¹ m
AnAm=0. (4)
В самом деле, если бы точка z входила в AnAm, то точки хn=z-rn, хm=z-rm были бы (очевидно, различными) точками множества A, т.е. представителями двух различных классов, чего быть не может, ибо их разность хn-хm=rm-rn есть число рациональное. Итак, (4) доказано.
С другой стороны, легко увидеть, что при любом k
AkÌ [- ![]() , +
, + ![]() ]
]
( ибо, если хÎAk, то x= x0+rk, где ÷ х0½£ 1/2, ½rk½£ 1), так что
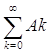 Ì [-
Ì [-![]() ,+
,+![]() ].
(5)
].
(5)
Из (5) и (4), в силу теоремы 6 следует, что
3=m*[- ![]() , +
, + ![]() ]
³
m*[
]
³
m*[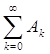 ] ³
] ³ 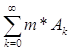 ,
,
откуда
a+a+a+… £ 3 и a=0
Сопоставляя (1) и (3), получим m*А<m*А, что и доказывает неизмеримость множества А.
Замечание. Если бы мы с самого начала разбили на классы не сегмент [-1/2, +1/2], а произвольное измеримое множество Е положительной меры, то, буквально повторяя проведенное рассуждение, пришли бы к неизмеримому множеству А Ì Е. Итак, всякое множество положительной меры содержит неизмеримую часть.