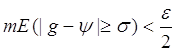Курсовая работа: Измеримые функции
Если каждому x из множества E
поставлено в соответствие некоторое число f(x),
то мы будем говорить, что на множестве E задана функция
f(x). При этом мы допускаем и бесконечные значения
функции, лишь бы они имели определенный знак, т.е. вводим «несобственные» числа
-![]() и +
и +![]() . Эти числа связаны между
собой и с любым конечным числом a неравенствами
. Эти числа связаны между
собой и с любым конечным числом a неравенствами
-![]() <a<+
<a<+![]() ,
,
и мы устанавливаем для них следующие законы действий:
+![]() ±a=+
±a=+![]() ,
+
,
+![]() +(+
+(+![]() )=+
)=+![]() , +
, +![]() -(-
-(-![]() )=+
)=+![]() ,
,
-![]() ±a=-
±a=-![]() ,
-
,
-![]() +(-
+(-![]() )=-
)=-![]() , -
, -![]() -(+
-(+![]() )=-
)=-![]() ,
,
½+![]() ½=½-
½=½-![]() ½=+
½=+![]() , +
, +![]() ×a=a×(+
×a=a×(+![]() )=+
)=+![]() ,
,
-![]() ×a=a×(-
×a=a×(-![]() )=-
)=-![]() , если a>0,
, если a>0,
+![]() ×a=a×(+
×a=a×(+![]() )=-
)=-![]() ,
,
-![]() ×a=a×(-
×a=a×(-![]() )=+
)=+![]() , если a<0
, если a<0
0×(±![]() )=(±
)=(±![]() )×0=0,
)×0=0,
(+![]() )×(+
)×(+![]() )=(-
)=(-![]() )×(-
)×(-![]() )=+
)=+![]() ,
,
(+![]() )×(-
)×(-![]() )=(-
)=(-![]() )×(+
)×(+![]() )=-
)=-![]() ,
,
![]() =0.
=0.
Здесь a обозначает вещественное конечное число. Символы
+¥-(+¥), -¥-(-¥), +¥+(-¥), -¥+(+¥).
![]() ,
, ![]()
мы считаем лишенными смысла.
Имея дело с функцией f (x), заданной на множестве E, мы будем символом
E(f>a)
обозначать множество тех x из множества Е, для которых выполнено неравенство f(x)>а.
Аналогичным образом вводятся символы
Е(f³а), Е(f=а), Е(f£а), Е(а<f£b)
и т.п. Если множество, на котором задана функция f(x), обозначено какой-либо другой буквой, например А или В, то мы соответственно будем писать
А(f>а), В(f>а)
и т.п.
Определение 1. Функция f(x), заданная на множество Е, называется измеримой, если измеримо это множество Е и если при любом конечном а измеримо множество
Е(f>а).
В связи с тем, что здесь речь идет о множествах, измеримых в смысле Лебега, часто (желая подчеркнуть именно это обстоятельство) говорят об измеримой (L) функции. Если же Е и все множества Е(f>а) измеримы (В), то и f(x) называется измеримой (В) функцией.
Теорема 1. Всякая функция, заданная на множестве меры нуль, измерима.
Это утверждение очевидно.
Теорема 2. Пусть f(x) есть измеримая функция, заданная на множестве Е. Если А есть измеримое подмножество Е, то f(x), рассматриваемая только для xÎА, измерима.
Действительно, А(f>а) =А×Е (f>а).
Теорема 3. Пусть f(x) задана на измеримом множестве Е, представимом в форме суммы конечного числа или счетного множества измеримых множеств Еk :
E=![]() ×
×
Если f(x) измерима на каждом из множеств ER., то она измерима и на Е.
В самом деле, E(f>a)= ![]() .
.
Определение 2. Две функции f(x) и g(x), заданные на одном и том же множестве Е, называются эквивалентными, если
mE (f¹g)=0
Обозначать эквивалентность функций f(x) и g(x) принято так:
f (x) ~g(x).
Определение 3. Пусть некоторое обстоятельство S имеет место для всех точек какого-нибудь множества Е, кроме точек, входящих в подмножество Е0 множества Е. Если mЕ0 = 0, то говорят, что S имеет место почти везде на множестве Е, или почти для всех точек Е.
В частности, множество исключительных точек Е0 может быть и пустым.
Теперь можно сказать, что две функции, заданные на множестве Е, эквиваленты, если они ровны почти везде на Е.
Теорема 4. Если f(х) есть измеримая функция, заданная на множестве Е, а g(x) ~ f(x), то g(x) также измерима.
Д о к а з а т е л ь с т в о. Пусть А = Е (f ¹ g), B = E – A. Тогда mA = 0, так что В измеримо. Значит функция f(x) измерима на множестве В. Но на множестве В функции f(x) и g(x) неотличимы, так что g(x) измерима на В. Поскольку g(x) измерима и на А (ибо mA = 0), она измерима на Е = А + В.
Теорема 5. Если для всех точек измеримого множества Е будет f(x) = c, то функция f(x) измерима.
Действительно,
E
(f > a) = ![]()
![]()
![]()
Заметим, что в этой теореме с может быть и бесконечным.
Функция f(x), заданная на сегменте [а, b], называется ступенчатой, если [а,b] разложить точками.
с0 = а< с1<с2<…<сn = b
на конечное число частей, в н у т р и которых (т.е. в интервалах (сk, ck + 1) при k = 0, 1, …., n –1) функция f(x) постоянна. Легко понять, что из теоремы 5 вытекает
Следствие. Ступенчатая функция измерима.
Теорема 6. Если f(x) есть измеримая функция, заданная на множестве Е, то при любом а измеримы множества
E (f ³ a), E (f = a), E (f £ a), E (f < a),
Д о к а з а т е л ь с т в о. Легко проверить, что
E (f ³ a) = 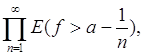
откуда следует измеримость множества E (f ³ a). Измеримость прочих множеств вытекает из соотношений:
E (f = a) = E(f ³ a) – E(f > a), E(f £ a) = E – E(f > a),
E (f < a) = E – E (f ³ a).
Замечание. Легко показать, что если хоть одно из множеств
E (f ³ a), E (f £ a), E (f < a)
оказывается измеримым при всяком а, то функция f(x) измерима на множестве Е (которое также предполагается измеримым).
Действительно, тождество 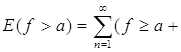
![]() )
показывает, например, что f(x) измерима, если измеримы все множества Е (f³а). Сходным образом устанавливаются и остальные
утверждения. Таким образом, в определении измеримой функции можно заменить
множество Е (f>a) любым из множеств (1).
)
показывает, например, что f(x) измерима, если измеримы все множества Е (f³а). Сходным образом устанавливаются и остальные
утверждения. Таким образом, в определении измеримой функции можно заменить
множество Е (f>a) любым из множеств (1).
Теорема 7. Если функция f(x), заданная на множестве Е,
измерима, а k конечное число, то измеримы и функции 1) f(x) + k, 2) kf(x), 3) çf (x)ç, 4) f2 (x), и если f(x) ¹0, то измерима и функция 5) ![]() .
.
Д о к а з а т е л ь с т в о. 1) Измеримость функции f(x) + k вытекает из соотношения Е (f+ k >a) = E (f>a- k).
2) Измеримость функции kf(x) при k =0 следует из теоремы 5. Для прочих k измеримость следует из очевидных соотношений
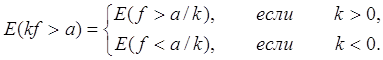
3) Функция çf(x) ç измерима потому, что
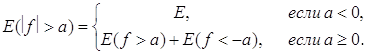
4) Аналогично, из того , что
E (f2 > a) =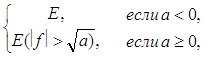
вытекает измеримость функции f 2 (x).
5) Наконец, при f(x) ¹ 0 имеем
![]() > a) =
> a) = 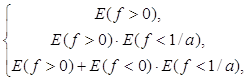
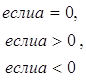
откуда и следует измеримость ![]() .
.
Теорема 8. Функция f(x), заданная и непрерывная на
сегменте Е=![]() , измерима.
, измерима.
Д о к а з а т е л ь с т в о. Прежде всего установим, что множество
F = E (f£ a)
замкнуто. Действительно, если x0 есть предельная точка этого множества и xn®x0 (x n ÎF ), то f(xn) £a и, в силу непрерывности f(x), будет f(x0 ) £a, т.е. x0 ÎF, что и устанавливает замкнутость множества F.
Но тогда множество Е (f>а) = Е – Е(f£а) измеримо, и теорема доказана.
Из самого определения измеримой функции следует, что функция, заданная на неизмеримом множестве, неизмерима.
Однако легко обнаружить существование неизмеримой функции, заданной на измеримом множестве.
Определение 4. Пусть М есть подмножество сегмента Е = [А, В]. Функция jм (х), равная единице на множестве М и нулю на множестве Е–М, называется характеристической функцией множества М.
Теорема 9. Множество М и его характеристическая функция jм одновременно измеримы или нет.
Д о к а з а т е л ь с т в о. Если функция jM (х) измерима, то измеримость множества М вытекает из соотношения
М = Е (jм > 0).
Обратно, если М есть измеримое множество, то соотношения
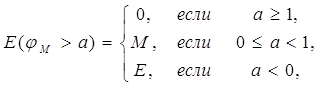
устанавливают измеримость функции jМ (х).
Отсюда, между прочим, весьма просто получаются примеры разрывных измеримых функций.
Дальнейшие свойства измеримых функций
Лемма. Если на множестве Е заданы две измеримые функции f(х) и g(х), то множество Е (f >g) измеримо.
Действительно, если мы перенумеруем все рациональные числа r1, r2, r3, …, то легко проверим справедливость соотношения
Е (f > g) = ![]() Е (f > rk)
Е (g < rk),
Е (f > rk)
Е (g < rk),
откуда и следует лемма.
Теорема 1. Пусть f(х) и g(х) суть конечные измеримые
функции, заданные на множестве Е. Тогда измерима каждая из функций 1) f(х) – g(х), 2) f(х) + g (х), 3) f(х) . g(х), и если g(х) ¹ 0, то измерима также функция 4)![]()
![]() .
.
Д о к а з а т е л ь с т в о. 1) Функция а + g(х) измерима при любом а. Значит (на основании леммы), множество Е (f > а+g ), а так как E(f-g>a)=E(f>a+g), то измерима функция f (х) – g(х).
2) Измеримость суммы f(х) + g(х) следует из того, что
f(х) + g(х) = f(х) – [ - g (х)].
3) Измеримость произведения f(x) .g(x) вытекает из тождества
f(x) .g(x)=![]() {[f(x)+g(x)]
{[f(x)+g(x)]![]() -[f(x)-g(x)]
-[f(x)-g(x)]![]() }
}
и теоремы 7
4) Наконец, измеримость частного
![]() есть следствие тождества
есть следствие тождества
![]() =f(x) ·
=f(x) ·![]() .
.
Эта теорема показывает, что действия арифметики, будучи применены к измеримым функциям, не выводят нас за пределы этого класса функций. Следующая теорема устанавливает сходный результат относительно уже не арифметической операции – предельного перехода.
Теорема 2. Пусть на множестве Е задана
последовательность измеримых функций f1(x), f2(x), … Если в каждой точке х![]() Е существует (конечный или
бесконечный) предел
Е существует (конечный или
бесконечный) предел
F(x)=![]() fn(x),
fn(x),
то функция F(х) измерима.
Д о к а з а т е л ь с т в о. Фиксируем произвольные а и введем в рассмотрение множества
![]() А
А![]() =Е(f
=Е(f![]() > a +
> a + ![]() ), В
), В![]() =
=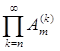 .
.
Эти множества, очевидно, измеримы, и для доказательства теоремы достаточно проверить, что
E(F>a) = ![]() .
.
Займемся же проверкой этого тождества.
Пусть х![]()
![]() Е (F>a), тогда F (x0) > a, и найдется такое натуральное m, что F(x0) > a +
1/m. Поскольку же fk (x)
Е (F>a), тогда F (x0) > a, и найдется такое натуральное m, что F(x0) > a +
1/m. Поскольку же fk (x) ![]() F (x0), то
найдется такое n, что при k
F (x0), то
найдется такое n, что при k![]() n будет
n будет
fk(x0) > a + ![]() .
.
Иначе говоря, х0 ![]() А
А![]() при всех k
при всех k![]() n, а тогда х0
n, а тогда х0 ![]() В
В![]() и тем более х0
и тем более х0![]()
![]() .
Отсюда следует, что Е (F > a)
.
Отсюда следует, что Е (F > a) ![]() .
.
Теперь остается установить обратное включение
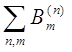
![]() E (F > a),
E (F > a),
и теорема будет доказана.
Пусть х0![]()
![]() . Тогда х0
. Тогда х0 ![]() В
В![]() при некоторых фиксированных
n и m. Это значит, что х0
при некоторых фиксированных
n и m. Это значит, что х0 ![]() А
А![]() для k
для k![]() n. Иначе говоря для k
n. Иначе говоря для k![]() n будет fk(x0) > a+1/m.
n будет fk(x0) > a+1/m.
Устремляя k к бесконечности и переходя в последнем неравенстве к пределу, получим, что F(x0)>a, т.е. x0 ÎE (F>a). Этим и доказано включение (*). Доказанная теорема допускает следующее обобщение.
Теорема 3. Пусть на множестве E заданы измеримые функции f1(x), f2(x), … и некоторая функция F(x). Если соотношение
![]() (a)
(a)
выполняется почти везде на Е, то F(x) измерима.
Д о к а з а т е л ь с т в о.
Обозначим через А множество всех точек X Î Е, в которых соотношение (a) не имеет места (в этих точках предела ![]() может вовсе не существовать). По условию, mA=0
и F(x) измерима на множестве А. По теореме 2 она измерима и
на множестве Е – А, а тогда она измерима и на всем множестве Е.
может вовсе не существовать). По условию, mA=0
и F(x) измерима на множестве А. По теореме 2 она измерима и
на множестве Е – А, а тогда она измерима и на всем множестве Е.
Последовательности измеримых функций. Сходимость по мере.
В этом месте нам придется рассматривать множества вида Е (|f – g| ³ s), Е (|f – g| < s), где f(x) и g(x) суть функции заданные не множестве Е, а s некоторое положительное число. При этом точки, в которых обе функции f(x) и g(x) принимают бесконечные значения одного знака, строго говоря, не входят ни в одно из этих множеств, поскольку в этих точках разность f(x) – g(x) лишена смысла. Так как указанное обстоятельство представляет известные неудобства, то мы раз и навсегда условимся эти точки относить к множеству Е (|f – g| ³ s). При таком соглашении очевидно
Е = Е (|f – g| ³ s) + Е (|f – g| < s)
и слагаемые правой части не пересекаются.
Теорема 1 (А. Лебег). Пусть на измеримом множестве Е задана последовательность измеримых и почти везде конечных функций f1(x), f2(x), f3(x), …, которая почти во всех точках Е сходится к почти везде конечной функции f(x). Тогда, каково бы ни было s>0, будет
![]()
Д о к а з а т е л ь с т в о. Отметим прежде всего, что в силу теоремы 3, предельная функция f(x) также измерима и, стало быть, измеримы те множества, о которых идет речь.
Положим
А = Е(|f| = + ¥), An = E(|fn| = + ¥), B = E (fn не ® f)
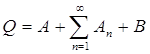 .
.
Очевидно,
MQ = 0 (1)
Пусть, далее,
![]() ,
, 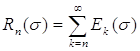 ,
, 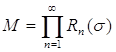 .
.
Все эти множества измеримы.
Так как R1(s)ÉR2(s)ÉR3(s)É…, то, в силу теоремы 12, при n ®¥ будет
mRn(s)®mM. (2)
Убедимся в том, что
MÌQ. (3)
В самом деле, если ![]() , то
, то ![]() , причем все числа f1(x0), f2(x0), … и их предел f (x0) – конечны. Значит найдется
такое n, что для k ³
n будет |fk(x0) – f(x0) <
s.
, причем все числа f1(x0), f2(x0), … и их предел f (x0) – конечны. Значит найдется
такое n, что для k ³
n будет |fk(x0) – f(x0) <
s.
Иначе говоря ![]() (k ³
n), а потому
(k ³
n), а потому ![]() и тем более
и тем более ![]() , откуда и следует (3).
, откуда и следует (3).
Но тогда, в силу (1), nM=0, и (2) принимает вид
![]() (4)
(4)
Этим и доказана теорема, ибо Еn(s) Ì Rn(s).
Замечание. Отметим, что нами установлен результат (4), более сильный, чем то, что мы хотели доказать. Ниже при доказательстве теоремы Д.Ф. Егорова, нам придется воспользоваться именно этим более сильным результатом.
Доказанная теорема дает повод установить следующее
Определение. Пусть на измеримом множестве Е задана последовательность измеримых и почти везде конечных функций
f1(x), f2(x), f3(x), …
и измеримая и почти везде конечная функция f(x). Если, каково бы ни было положительное число s, оказывается, что
![]() ,
,
то говорят, что последовательность (*) сходится к функции f (x) по мере.
Мы будем, следуя Г.М.Фихтенгольцу, обозначать сходимость по мере символом
fn(x) Þ f(x).
С помощью понятия сходимости по мере можно формулировать теорему Леберга так.
Теорема 1*. Если последовательность функций сходится почти везде, то она сходится и по мере к той же предельной функции.
Следующий пример показывает, что эта теорема необратима.
П р и м е р . Определим на полусегменте [0, 1) для каждого натурального k группу из k функций: f1(k) (x), f2(k) (x), …, fk(k) (x), полагая
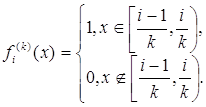
В частности, f1(1) (x) º 1 на [0, 1). Нумеруя все построенные функции подряд одним значком, мы получим последовательность
j1 (x) = f1(1) (x), j2 (x) = f1(2) (x), j3 (x) = f2(2) (x), j4 (x) = f1(3) (x), …
Легко видеть, что последовательность функций jn (x) сходится по мере к нулю. В самом деле, если jn (x) = fi(k) (x), то при любом s>0 будет
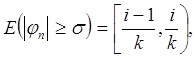
и мера этого множества, равная 1/k, стремится к нулю с возрастанием n.
Вместе с тем, соотношение jn (x)®0 не выполняется ни в одной точке промежутка [0, 1).
Действительно, если 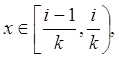 так что fi(k) (x0) = 1. Иначе говоря, как далеко
мы не продвинемся вдоль ряда чисел j1 (x0), j2 (x0), j3 (x0), …, мы всегда будем встречать
в этом ряду числа, равные 1, что и доказывает наше утверждение.
так что fi(k) (x0) = 1. Иначе говоря, как далеко
мы не продвинемся вдоль ряда чисел j1 (x0), j2 (x0), j3 (x0), …, мы всегда будем встречать
в этом ряду числа, равные 1, что и доказывает наше утверждение.
Таким образом, понятие сходимости по мере есть понятие, существенно более общее, чем понятие сходимости почти везде и тем более, чем понятие сходимости везде.
Естественно спросить, в какой степени соотношение
fn(x) Þ f(x)
определяет функцию f(x), т.е. единственна ли предельная функция при сходимости по мере.
Теоремы 2 и 3 позволяют ответь на этот вопрос.
Теорема 2. Если последовательность функций fn(x) сходится по мере к функции f(x), то эта же последовательность сходится по мере ко всякой функции g(x), эквивалентной функции f(x).
Д о к а з а т е л ь с т в о. При любом s > 0 будет
E( êfn – g ê ³ s ) Ì E( f ¹ g) + E( çfn - f ç ³ s),
откуда (поскольку mE (f ¹ g) = 0)
mE (êfn – g ê³ s) £ mE(çfn – f ç³ s),
что и доказывает теорему.
Теорема 3. Если последовательность функций fn(x) сходится по мере к двум функциям f(x) и g(x), то эти предельные функции эквивалентны.
Д о к а з а т е л ь с т в о. Легко проверить, что при s > 0 будет
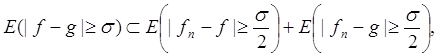 (*)
(*)
ибо точка, не входящая в правую часть этого соотношения, и подавно не может входить и в левую часть. Но соотношения
fn Þ f, fn Þ g
показывают, что мера правой части (*) стремится к нулю с возрастанием n, откуда ясно, что mE (êfn – g ê³ s) = 0.
Но так как
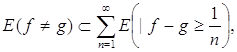
то f ~g, что и требовалось доказать.
Теоремы 2 и 3 показывают, что, желая восстановить свойство единственной предельной функции для сходимости по мере, мы должны были бы условиться считать эквивалентные функции за тождественные. Это обычно и делается в метрических вопросах теории функций, т.е. в тех вопросах, где все свойства функций изучаются с помощью меры множеств, на которых функция обладает или не обладает тем или другим свойством. В интегральном исчислении мы надем много примеров подобного подхода к вещам.
Хотя сходимость по мере общее сходимости почти везде, имеет место все же следующая теорема.
Теорема 4 (Ф.Рисс). Пусть {fn(x)} последовательность функций, которая сходится по мере к функции f(x). В таком случае существует подпоследовательность
fn1(x), fn2(x), fn3(x), ... (n1<n2<n3<...),
сходящаяся к функции f(x) почти везде.
Д о к а з а т е л ь с т в о. Возьмем последовательность положительных чисел s1>s2>s3>¼, для которой lim sk=0.
Пусть, далее, h1+h2+h3+¼ (hk>0) есть сходящийся положительный ряд.
Теперь мы можем построить требуемую последовательность индексов
n1 < n2 < n3 < ... (*)
следующим образом: обозначим через n1 натуральное число, для которого
mE(½fn1-f½³s1)<h1.
Такое число обязательно существует, ибо
mE(½fn-f½³s1)®0 при n®¥.
Затем через n2 обозначим то натуральное число, для которого
mE(½fn2-f½³s2)h2, n2>n1.
Вообще через nk мы обозначаем такое число, что
mE(½fnk-f½³sk)< hk, nk>nk-1.
Последовательность (*), таким образом, построена.
Теперь установим, что почти везде на множестве E будет
![]() (**)
(**)
Действительно, пусть
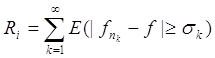 ,
, 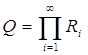 .
.
Так как R1ÉR2ÉR3É..., то (теорема 12)
mRi®mQ
C другой стороны, очевидно, что 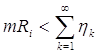 так что mRi®0 и, стало быть, mQ=0.
так что mRi®0 и, стало быть, mQ=0.
Остается проверить, что соотношение (**) имеет место для всех x из множества E - Q.
Пусть x0 Î E - Q. Тогда x0 ![]() Rio. Иначе говоря, при k ³ i0
Rio. Иначе говоря, при k ³ i0
x0![]() E(|fnk-f|³sk),
E(|fnk-f|³sk),
и, следовательно,
|fnk(x0) – f(x0)|<sk, (k ³ i0)
и, поскольку sk®0, ясно, что fnk(x0) ®f(x0).
Теорема доказана.
Теорема Лебега дала повод к установлению понятия сходимости по мере. С другой стороны, с помощью этой же теоремы можно установить весьма важную теорему Д.Ф.Егорова.
Теорема 5 (Д.Ф.Егоров). Пусть на измеримом множестве Е задана последовательность измеримых и почти везде конечных функций f1(x), f2(x), f3(x), …, почти везде сходящаяся к измеримой и почти везде конечной функции f (x):
![]()
В таком случае, для любого d>0 существует такое измеримое множество Еd![]() Е, что:
Е, что:
1) mEs >mE - d;
2) на множестве Ed стремление(*) происходит равномерно.
Д о к а з а т е л ь с т в о. При доказательстве теоремы Лебега было установлено, что при любом s >0 будет
![]() (1)
(1)
где 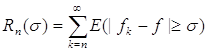 .
.
Заметив это, возьмем сходящийся положительный ряд
h1+h2+h3+... (hi>0)
и стремящуюся к нулю последовательность положительных чисел
s1>s2>s3>…, lim si=0.
В силу (1), можно каждому натуральному i соотнести такое натуральное ni, что mRni(si)< hi.
Сделав это, найдем такое i0, что 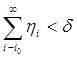 (где d число, фигурирующее в
формулировке теоремы), и положим
(где d число, фигурирующее в
формулировке теоремы), и положим 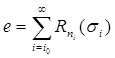 .
.
Очевидно,
me<d.
Пусть Еd = Е – е. Установим, что множество Еd требуемое. Неравенство mEd > mE - d ясно, так что остается убедиться в равномерности стремления
fn(x)®f(x)
на множестве Еd.
Пусть e > 0. Найдем i такое, что i ³ i0, si < e, и покажем, что при k ³ ni и при всех x Î Еd будет
|fk(x) – f(x)| < e,
откуда и будет следовать теорема.
Если x Î Еd , то х![]() e. Значит в частности, x
e. Значит в частности, x![]() Rni(si).
Rni(si).
Иначе говоря, при k ³ ni
x ÎE(|fk – f|³ si),
так что
|fk(x) – f(x)| <si (k ³ ni)
и тем более
|fk(x) – f(x)| < e (k ³ ni).
Теорема доказана, ибо ni зависит только от e, но не от x.
Структура измеримых функций
При изучении какой-нибудь функции сам собою встает вопрос о точном или приближенном представлении ее с помощью функций более простой природы.
Таковы, например, алгебраические вопросы о разложении многочлена на множители или рациональные дроби на простейшие. Таков же вопрос о разложении непрерывной функции в степенной или тригонометрический ряд и т.п.
В этой части мы устанавливаем различные теоремы о приближении измеримых функций функциями непрерывными, т.е. решаем сходный вопрос для измеримых функций. Эти теоремы позволяют нам найти основное структурное свойство измеримой функции выражаемой теоремой 4.
Теорема 1. Пусть на множестве Е задана измеримая, почти везде конечная функция f(x). Каково бы ни было e > 0, существует измеримая ограниченная функция g(x), такая, что mE(f¹g)< e.
Д о к а з а т е л ь с т в о. Положим
Аk = E(|f|>k), Q = E(|f| = + ¥).
По условию, mQ = 0. Ввиду очевидных соотношений
А1 É А2
É А3 É …,
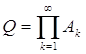
будет (теорема 12) при k®¥
mAk®mQ = 0.
Значит, найдется такое k0, что mAk0<e.
Определим на множестве E функцию g(x), полагая
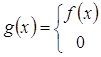
![]()
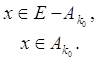
![]()
Эта функция измерима и, кроме того, ограничена, поскольку g (x)ê k0. Наконец, E(f ¹ g) = Ako, что и доказывает теорему.
Доказанная теорема означает, что всякая измеримая и почти везде конечная функция становится ограниченной, если пренебречь множеством сколь угодно малой меры.
Определение. Пусть функция F(x) задана на множестве E и x0ÎE, причем F(x0) ¹±¥. Говорят, что функция F(x) непрерывна в точке х0 в двух случаях: 1) если х0 есть изолированная точка E; 2) если х0Î E¢ и соотношения xn®x0, xnÎE влекут соотношение
f(xn) ®f(x0).
Если f(x) непрерывна в каждой точке множества E, то говорят, что она непрерывна на этом множестве.
Лемма 1. Пусть множества F1, F2, …, Fn замкнуты и попарно не пересекаются. Если функция j (х), заданная на множестве
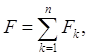
постоянна на каждом из множеств Fk, то она непрерывна на множестве F.
Д о к а з а т е л ь с т в о. Пусть x0ÎF’ и xi®x0, xiÎF.
В силу замкнутости множества F точка x0 принадлежит этому множеству и, стало быть, найдется такое m, что x0ÎFm.
Но множества Fk попарно не пересекаются.
Значит, если k¹m, то х0![]() Fk и, в силу замкнутости множества
Fk, точка x0 не является и предельной точкой
этого множества.
Fk и, в силу замкнутости множества
Fk, точка x0 не является и предельной точкой
этого множества.
Отсюда следует, что в последовательности {xi} может быть только конечное число точек, принадлежащих множеству Fk при k¹m. Отметим все члены последовательности, которые входят в одно из множеств F1, …, Fm-1, Fm+1, …, Fn, и пусть xi0, последний из них. Тогда при i > i0 необходимо будет x1ÎFm, т.е. при i > i0 оказывается j (xi) = j (x0), а это доказывает лемму.
Лемма 2. Пусть F есть замкнутое множество, содержащееся в сегменте [a, b]. Если функция j(x) задана и непрерывна на множестве F, то можно определить на [a, b] функцию y(x) со следующими свойствами
1) y(x) непрерывна;
2) если xÎF, то y(x)= j(x);
3) max |y(x)| = max |j(x)|.
Д о к а з а т е л ь с т в о. Обозначим через [a, b] наименьший сегмент, содержащий множество F. Если бы требуемая функция y(x) была уже построена на сегменте [a, b], то достаточно было бы дополнить ее определение, полагая
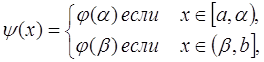
чтобы получить требуемую функцию уже на всем сегменте [a, b].
Поэтому, не ограничивая общности, можно считать что [a, b] и есть наименьший сегмент, содержащий множество F.
Если F = [a, b], то теорема тривиальна. Будем считать, что F ¹ [a, b]. Тогда множество [a, b] – F состоит из конечного или счетного множества взаимно не налегающих интервалов, концы которых принадлежат F (дополнительных интервалов множества F).
Зададим функцию y(x), полагая ее равной j(x) в точках множества F и линейной на всех дополнительных интервалах.
Убедимся в непрерывности этой функции. Непрерывность ее в каждой точке множества [a, b] – F очевидна.
Пусть х0 есть точка множества F . Мы покажем, что функция y(x) непрерывна в этой точке слева (непрерывность справа устанавливается совершенно аналогично).
Если точка х0 служит правым концом какого-нибудь дополнительного интервала, то непрерывность функции y(x) в этой точке слева очевидна.
Пусть же x0 не является правым концом никакого дополнительного интервала и пусть x1< x2< x3<… последовательность точек, стремящихся к x0.
Если xnÎF (n = 1, 2, 3, …) то, используя непрерывность на
множестве F функции j(x), имеем y(xn) = j(xn) ® j(x0) =y(x0). Поэтому можно считать, что хn![]() F (n = 1, 2, 3, …).
F (n = 1, 2, 3, …).
В таком случае точка x1 попадает в какой-то дополнительный интервал (l1, m1), причем m1<х0. Продолжая это рассуждение, мы приходим к последовательности (l1, m1), (l2, m2), (l3, m3), … дополнительных интервалов, расположенных в порядке номеров слева направо и таких, что
XkÎ(l1, m1) (k = ni-1+1, …, ni).
Соотношение xni<mi<x0 показывает, что mi, а из того, что mi-1£li< x0, ясно, что и li ®x0.
Но li и mi входят в F, так что
lim y(li) = lim y(mi) = y( x0).
Ввиду того, что значения линейной функции в каком-нибудь интервале лежат между ее значениями на концах этого интервала, ясно, что и limy(xn)=y(x0).
Итак, непрерывность функции y(x) доказана.
Из самого ее построения видно, что она совпадает с j(x) на множестве F.
Наконец по известной теореме Вейерштрасса, среди значений непрерывной на сегменте функции |y(x)| есть наибольшее – max |y(x)|. Легко видеть, что этот максимум достигается именно в точке, принадлежащей множеству F, ибо на дополнительных интервалах функция y(x) линейна. Поэтому max |y(x)| = max |j(x)|.
Лемма доказана полностью.
Теорема 2 (Э. Борель). Пусть на сегменте [a, b] задана измеримая и почти везде конечная функция f(x). Каковы бы ни были числа s >0 и e >0 существует непрерывная на [a, b] функция y(x), для которой
mE(|f-y| ³ s) <e
Если при этом |f(x)| £ K, то можно и y(x) выбрать так, что |y(x)| £ K.
Д о к а з а т е л ь с т в о. Предположим сначала, что |f(x)| £ K, т.е. что функция f(x) ограничена.
Фиксируя произвольные s >0 и e >0, найдем столь большое натуральное m, что K/m<s, и построим множества
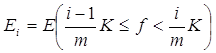 (i = 1 – m, 2 – m, …, m
– 1)
(i = 1 – m, 2 – m, …, m
– 1)
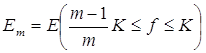
Эти множества измеримы, попарно не пересекаются и
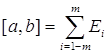
Построим для
каждого i замкнутое множество Fi Ì Ei с мерой ![]() и положим
и положим 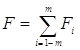 .
.
Ясно, что ![]() , откуда m[a, b] – mF<e.
, откуда m[a, b] – mF<e.
Зададим теперь на множестве F функцию j(x), полагая
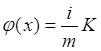 при xÎFi (i = 1 – m, …, m).
при xÎFi (i = 1 – m, …, m).
В силу леммы 1 эта функция непрерывна на множестве F, |j(x)| £ K и, наконец, при xÎF будет |f(x) - j(x)| < s.
Остается применить лемму 2. Это приводит к непрерывной функции y(x), совпадающей на множестве F с функцией j(x), причем |j(x)|³K. Поскольку E ( | f - y | ³ s ) Ì [a , b] – F , ясно, что функция y(x) требуемая.
Итак, для ограниченной функции теорема доказана.
Допустим теперь, что f (x) не ограничена. Тогда, пользуясь теоремой 1, можно построить такую ограниченную функцию g(x), что mE (f ¹ g) < e/2.
Применяя уже доказанную часть теоремы к функции g(x), мы найдем такую непрерывную функцию y(x), что
E (|f-y| ³ s) Ì E (f ¹ g) + E (|g-y| ³ s),
Так что функция y(x) решает задачу.
Следствие. Для всякой измеримой и почти везде конечной функции f(x), заданной на сегменте [a, b], существует последовательность непрерывных функций yn(x), сходящаяся по мере к функции f(x).
В самом деле, взяв две стремящиеся к нулю последовательности
s1>s2>s3>…, sn®0,
e1>e2>e3>…, en®0,
построим для каждого n такую непрерывную функцию yn(x), что
mE(|f-yn|³sn)< en
Легко видеть, что yn(x) Þ f(x).
Действительно, какое бы s > 0 ни взять, для n ³ n0 будет sn<s, а для таких n
![]()
откуда и следует наше утверждение.
Применив к последовательности {yn(x)} теорему Ф. Рисса мы приходим к последовательности непрерывных функций {ynk(x)}, которая сходится к функции f(x) почти везде.
Иначе говоря установлена
Теорема 3 (М.Фреше). Для всякой измеримой и почти везде конечной функции f(x), заданной на сегменте [a, b], существует последовательность непрерывных функций, сходящаяся к f(x) почти везде.
С помощью этой теоремы легко устанавливается весьма замечательная и важная
Теорема 4 (Н. Н. Лузин). Пусть f(x) измеримая и почти везде конечная функция, заданная на [a, b]. Каково бы ни было d > 0, существует такая непрерывна функция j(x), что
mE(f ¹ j) < d
Если, в частности, |f(x)| £ K, то и |j(x)| £ K.