Курсовая работа: Инвариантность стационарного распределения трехузловой сети массового обслуживания
Раздел: Рефераты по математике
Тип: курсовая работа
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
Учреждение образования
“Гомельский Государственный университет
имени Франциска Скорины"
Математический факультет
Кафедра математического анализа
Курсовая работа
Инвариантность стационарного распределения трехузловой сети массового обслуживания
Исполнитель
Студентка группы М-42 Грамович Е.Г.
Научный руководитель
Кандидат физико-математических
наук, старший преподаватель Якубович О.В.
Гомель 2004
Содержание
Введение
1. Теоретические сведения
1.1 Марковские процессы
1.2 Простейший поток
1.3 Время обслуживания
1.4 Классификация систем массового обслуживания
1.5 Марковские системы массового обслуживания
1.6 Марковские сети массового обслуживания
1.7 Нахождение стационарных вероятностей состояний открытой марковской сети массового обслуживания
1.8 Нахождение решения для немарковского случая
2. Марковский случай
2.1 Описание модели
2.2 Сеть массового обслуживания
2.3 Уравнения равновесия
2.4 Нахождение стационарных вероятностей
2.5 Условия эргодичности
3. Немарковский случай
3.1 Описание модели
3.2 Составление дифференциально-разностных уравнений
3.3 Поиск решения дифференциально-разностных уравнений
Список литературы
Введение
Математическая теория массового обслуживания является разделом теории случайных процессов, изучающим определенный класс задач, которые возникают на практике, когда заявки, нуждающиеся в обслуживании, прибывают к некоторому обслуживающему устройству. В качестве примеров заявок и обслуживающих их устройств можно назвать абонентские вызовы, поступающие на телефонный коммутатор, станки, ожидающие обслуживание рабочими, автомобили, ожидающие у дорожного пересечения, самолёты, прибывающие в аэропорт, суда, заходящие в порт и т.д.
Системами (моделями) массового обслуживания называют математические модели систем, которые предназначены для обслуживания заявок, поступающих через случайные промежутки времени, причем длительность обслуживания в общем случае также случайна.
Системы массового обслуживания описываются заданием:
входящего потока заявок;
совместного распределения времен обслуживания заявок;
числа обслуживающих приборов (линий);
дисциплины обслуживания, организации очереди и процесса обслуживания.
В данной курсовой работе рассматривается система массового обслуживания для которой:
1) входящий поток заявок является пуассоновским;
2) в системе три обслуживающих прибора;
A) Марковский случай.
3 время обслуживания экспоненциальное
4 дисциплина обслуживания FIFO;
Б) Немарковский случай.
3) время обслуживания определяется с помощью произвольной
функцией распределения времени ![]() обслуживания
обслуживания
![]() -м прибором одной заявки,
такой что
-м прибором одной заявки,
такой что
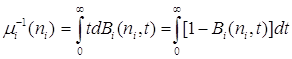 ;
;
4) дисциплина обслуживания LCFS PR; (заявка, поступающая в ![]() -ый узел, вытесняет заявку
с прибора и начинает обслуживаться, вытесненная заявка идет в начало очереди).
-ый узел, вытесняет заявку
с прибора и начинает обслуживаться, вытесненная заявка идет в начало очереди).
В курсовой работе для открытой марковской сети массового обслуживания составим уравнения равновесия, найдем стационарные вероятности, установим условия эргодичности. Для не марковского случая составим дифференциально-разностное уравнение в частных производных для процесса, дополненного остаточными временами, найдем решение данного уравнения. Сравним марковский и немарковский случай. Сделаем вывод.
1. Теоретические сведения
1.1 Марковские процессы
Пусть Т и Х - некоторые подмножества числовой прямой R.
Определение 1. Случайный процесс ![]() со
значениями в Х называется марковским, если для любых
со
значениями в Х называется марковским, если для любых ![]() из Т и любых борелевских
множеств
из Т и любых борелевских
множеств ![]() из R
из R
![]()
Другими словами, марковский процесс это такой случайный процесс, у которого при фиксированном настоящем будущее не зависит от прошлого. Если Х={i} конечно или счётно, то марковский процесс называют цепью Маркова. Если вероятности
![]()
не зависят от s, а зависят от t, то цепь Маркова называется однородной. Цепь Маркова с T={0,1,2,... } называют цепью с дискретным временем, цепь Маркова c
![]()
называют цепью с непрерывным временем.
Обозначим
![]()
![]() называют
вероятностями перехода из состояния i в состояние j за время t.
Для цепи Маркова с дискретным временем обозначают
называют
вероятностями перехода из состояния i в состояние j за время t.
Для цепи Маркова с дискретным временем обозначают ![]() и
называют вероятностями перехода из i в j за n шагов.
и
называют вероятностями перехода из i в j за n шагов.
Вероятностями перехода за 1 шаг ![]() называют
просто вероятностями перехода. Набор вероятностей
называют
просто вероятностями перехода. Набор вероятностей ![]() называют
начальным распределением цепи Маркова.
называют
начальным распределением цепи Маркова.
Определение 2. Цепь Маркова называется эргодической, если при
![]()
![]() .
.
Если все ![]() , то
цепь называется строго эргодической.
, то
цепь называется строго эргодической.
Набор ![]() называется
эргодическим распределением,
называется
эргодическим распределением, ![]() называются
финальными вероятностями.
называются
финальными вероятностями.
Определение 3. Распределение вероятностей ![]() называется стационарным
распределением, если
называется стационарным
распределением, если
![]() - распределение
вероятностей, то есть
- распределение
вероятностей, то есть ![]() и
и ![]()
![]() для всех
для всех ![]() .
.
Определение 4. Однородная марковская цепь называется
неприводимой, если для любых двух состояний i и j, ![]() существует
существует
![]() такое, что
такое, что ![]() .
.
Определение 5. Однородная марковская цепь называется
эргодической, если для любых начальных распределений абсолютное распределение ![]() всегда сходятся к одному и
тому же распределению, которое является единственным стационарным
распределением цепи:
всегда сходятся к одному и
тому же распределению, которое является единственным стационарным
распределением цепи:
![]() для всех
для всех ![]()
Теорема (Эргодическая теорема Фостера).
Регулярная Марковская цепь с непрерывным временем и счетным числом состояний эргодична, если она неприводима и система уравнений
![]()
имеет нетривиальное решение ![]() такое,
что
такое,
что ![]()
При этом существует единственное стационарное распределение, которое совпадает с эргодическим.
1.2 Простейший поток
Если у рекуррентного потока
![]() ,
,
то такой поток называется простейшим или пуассоновским потоком.
Определение 1. Если промежутки времени между моментами поступления заявок независимы и имеют показательное распределение с параметром l, то поток заявок называется простейшим или пуассоновским с параметром l.
Для простейшего потока вероятность поступления k заявок в промежутке времени [0,t) равна:
![]() (k=0,1,2,…) (1)
(k=0,1,2,…) (1)
Определение 2. Поток
заявок называется стационарным, если для любых попарно непересекающихся
интервалов времени ![]() вероятность поступления в
них соответственно
вероятность поступления в
них соответственно ![]() заявок зависит
только от этих чисел и от длин
заявок зависит
только от этих чисел и от длин ![]() и не
зависит от их расположения на временной оси.
и не
зависит от их расположения на временной оси.
Определение 3. Поток заявок называется потоком без последействия, если вероятность поступления k заявок в течение промежутка времени [T,T+t) не зависит от того, сколько требований и каким образом поступало до момента Т.
Определение 4. Поток
заявок называется ординарным, если для ![]() ,
где
,
где ![]() вероятность поступления
двух или более заявок в промежутке
вероятность поступления
двух или более заявок в промежутке ![]() .
.
Определение 5. Простейшим потоком называется стационарный ординарный поток без последействия.
Определение 6. Стационарный поток, для которого вероятность поступления k заявок за время t равна:
![]() (k=0,1,2,…; l>0),
(k=0,1,2,…; l>0),
называется простейшим или пуассоновским потоком с параметром l.
В силу (1) среднее число заявок, поступающих за время t, равно lt. Значит l - среднее число заявок, поступающих в единицу времени. Поэтому l называют интенсивностью пуассоновского потока.
1.3 Время обслуживания
Рассмотрим работу обслуживающего прибора (канала, линии). В
общем случае длительности обслуживания заявок представляют из себя
неотрицательные величины. ![]()
![]() предполагают статистически
независимой от поступающего на прибор потока заявок.
предполагают статистически
независимой от поступающего на прибор потока заявок.
Определение 1. Говорят, что обслуживание задано, если для любого
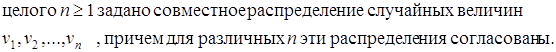 Определение
2. Обслуживание называется рекуррентным, если
Определение
2. Обслуживание называется рекуррентным, если ![]()
Определение 3. Рекуррентное обслуживание с
![]()
(показательным) обслуживанием с параметром m. Если
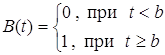
Т. е. время обслуживания любой заявки неслучайно (и равно b единиц времени), то обслуживание называют детерминированным или регулярным.
1.4 Классификация систем массового обслуживания
Классификация систем массового обслуживания чаще всего производят по следующим признакам:
входящий поток заявок;
совместное распределение времен обслуживания заявок;
число обслуживающих приборов (каналов, линий);
дисциплина обслуживания, организация очереди и процесса обслуживания.
Существуют следующие типы систем. В системах с потерями заявки, которые при поступлении не находят ни одного свободного прибора, теряются. Для систем с ожиданием возможно ожидание любого числа требований, которые не могут быть обслужены сразу. Для систем с ограниченным числом мест для ожидания ожидать может только число заявок, меньше некоторого фиксированного числа N+1. Если заявка поступающая в систему, застает очередь из N заявок, она теряется для системы. Для заявок, стоящих в очереди к обслуживающим приборам, с помощью некоторой дисциплины обслуживания определяется, в каком порядке ожидающие заявки выбираются из очереди на обслуживание. Важнейшими дисциплинами обслуживания являются:
FIFO (first in - first out) заявки обслуживаются в порядке поступления;
LIFO (last in - first out) инверсионный порядок обслуживания, при котором в первую очередь обслуживается заявка, поступившая последней;
SIRO (service in random order) очередная заявка выбирается наудачу.
Для обозначения простых процессов обслуживания используются обозначения, предложенные Кендалом:
А/B/n/N.
Буква А характеризует поток требований: например, А=М - пуассоновский поток. Буква B характеризует случайные последовательности длительностей обслуживания на отдельных приборах: B=M - экспоненциальное обслуживание (с одинаковой интенсивностью для разных приборов). Буква n означает количество обслуживающих приборов, буква N - количество мест для ожидания заявок в очереди.
1.5 Марковские системы массового обслуживания
К марковским системам относятся системы, поведение которых в
момент времени t может быть описано марковским процессом ![]() . В частности, сюда
относятся все системы вида M/M/n/N, где
. В частности, сюда
относятся все системы вида M/M/n/N, где ![]() .
Действительно, пусть
.
Действительно, пусть ![]() обозначает число
заявок в системе в момент t. Вероятностное
распределение
обозначает число
заявок в системе в момент t. Вероятностное
распределение ![]() после момента
t определяются:
после момента
t определяются:
1) числом заявок в системе в момент t;
2) моментами поступления заявок после момента t;
3) моментами окончаний обслуживания заявок после момента t.
В силу того, что входной поток простейший, моменты поступления
заявок после момента t не зависят от предыстории
системы до момента t. Аналогично, поскольку
времена обслуживания показательно распределены, из-за “отсутствия памяти” у
показательного распределения моменты окончания обслуживания заявок после момента
t не зависят от предыстории системы до момента t. Поэтому вероятностное поведение ![]() после момента t зависит только от
после момента t зависит только от ![]() и
не зависит от поведения
и
не зависит от поведения ![]() до
момента t. Значит
до
момента t. Значит ![]() -
марковский процесс с конечным или счетным числом состояний. Поэтому для
нахождения зависящих от времени вероятностей состояний
-
марковский процесс с конечным или счетным числом состояний. Поэтому для
нахождения зависящих от времени вероятностей состояний ![]() следует решить систему
уравнений Колмогорова для безусловных вероятностей. Если интерес представляет
стационарные вероятности, то следует решить систему уравнений равновесия. Для
получения уравнений Колмогорова используется предельный переход при Dt®¥, который называется Dt -методом.
следует решить систему
уравнений Колмогорова для безусловных вероятностей. Если интерес представляет
стационарные вероятности, то следует решить систему уравнений равновесия. Для
получения уравнений Колмогорова используется предельный переход при Dt®¥, который называется Dt -методом.
1.6 Марковские сети массового обслуживания
Сеть массового обслуживания представляет собой совокупность
систем массового обслуживания, в которой циркулируют заявки, переходящие из
одной системы в другую. Предположим, что сеть состоит из n
систем массового обслуживания (СМО) ![]() каждая
из которых имеет неограниченное число мест для ожидания.
каждая
из которых имеет неограниченное число мест для ожидания.
Под состоянием сети в момент времени t будем понимать вектор:
![]()
где ![]() - число заявок в
i-ой СМО (на обслуживание и в очереди).
- число заявок в
i-ой СМО (на обслуживание и в очереди).
Сети массового обслуживания разделяют на два типа: замкнутые
и открытые (разомкнутые). В замкнутой сети обслуживания постоянное число заявок
![]() , то есть заявки не
поступают извне и не уходят из сети. В открытую сеть заявки поступают из
внешних источников и после завершения обслуживания могут покидать её.
, то есть заявки не
поступают извне и не уходят из сети. В открытую сеть заявки поступают из
внешних источников и после завершения обслуживания могут покидать её.
Традиционный подход в описании моделей сетей массового обслуживания зависит от ряда предположений из теории стохастических процессов, например:
Переходы заявок между СМО сети описываются неприводимой цепью Маркова.
Заявки стохастически независимы.
Существует стационарный режим, работа сети может быть описана стационарным стохастическими процессами.
Времена обслуживания заявок в СМО сети распределены по показательному закону.
1.7 Нахождение стационарных вероятностей состояний открытой марковской сети массового обслуживания
Пусть входящий в открытую марковскую сеть массового
обслуживания поток заявок описывается чистым процессом размножения с
интенсивностью , причем в i-ую систему
массового обслуживания входящая заявка поступает с вероятностью ![]() . Времена обслуживания
заявок в i-той системе массового обслуживания распределены по
показательному закону
. Времена обслуживания
заявок в i-той системе массового обслуживания распределены по
показательному закону ![]() , зависящим от
текущего числа заявок в i-той системе
, зависящим от
текущего числа заявок в i-той системе ![]() i=1,...,n.
i=1,...,n.
Дисциплины обслуживания заявок в системе сети FIFO. Переходы
заявок между системами, а также уход заявки из сети описывается неприводимой
цепью Маркова. Заявка, завершающая обслуживание в системе ![]() , переходит с вероятностью
, переходит с вероятностью ![]() в систему
в систему ![]() ,
, ![]() есть вероятность ухода
заявки из i-ой системы массового обслуживания сети.
есть вероятность ухода
заявки из i-ой системы массового обслуживания сети.
![]()
В этом случае многомерный процесс N (t), определяющий состояние сети, является многомерным аналогом процесса размножения и гибели. Предположим, что существует стационарное распределение
![]() ,
,
принимает все возможные значения. Тогда, аналогично как и для одномерного процесса размножения и гибели, можно показать, что стационарное распределение единственно и удовлетворяет системе уравнений равновесия (баланса), которая представляет собой систему линейных разностных уравнений:
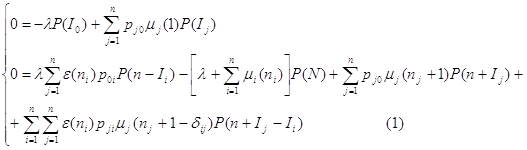
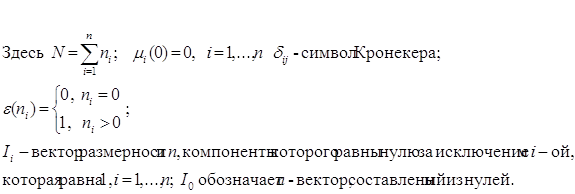
Для упрощения системы (1) введем величины ![]() так, что
так, что ![]() есть полная интенсивность
поступления заявок в системы
есть полная интенсивность
поступления заявок в системы ![]() . Интенсивность
. Интенсивность
![]() состоит из интенсивности
потока заявок, поступающих извне
состоит из интенсивности
потока заявок, поступающих извне ![]() , и
интенсивности поступления заявок в систему
, и
интенсивности поступления заявок в систему ![]() от
других СМО, в том числе и от самой системы
от
других СМО, в том числе и от самой системы ![]() .
.
Поэтому ![]() (2).
(2).
Из (2) получим ![]() (3).
(3).
Соотношение (2) иногда называют законом сохранения потока заявок. Оно говорит о том, что интенсивность входящего потока заявок в i-тую СМО, i=1,...,n, в стационарном режиме равна интенсивности входящего потока заявок из этой системы.
Теорема1. (Джексона) Стационарное распределение может быть найдено в виде:
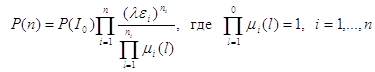
1.8 Нахождение решения для немарковского случая
Составив и решив систему дифференциально-разностных уравнений, найдется вид функции распределения
![]()
для случайного процесса ![]() .
Тогда можно найти
.
Тогда можно найти ![]() и
и ![]() .
.
Так что нахождение функций
![]()
решит поставленную задачу.
2. Марковский случай
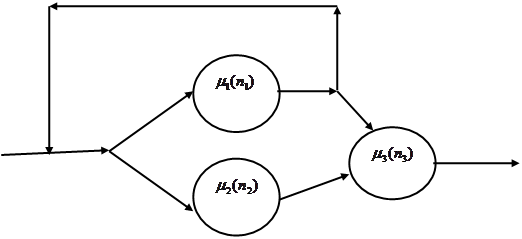
2.1 Описание модели
![]()
![]()
![]()
![]()
![]() 1
1
![]()
2.2 Сеть массового обслуживания
Дана открытая марковская сеть массового обслуживания, состоящая из трех подсистем. Состояние сети в момент времени t определяется вектором
![]()
число заявок в i-ой
подсистеме в момент времени t. Входящий поток является
пуассоновским потоком с параметром ![]() . Времена
обслуживания заявок в i-ой системе массового
обслуживания распределены по показательному закону с параметром
. Времена
обслуживания заявок в i-ой системе массового
обслуживания распределены по показательному закону с параметром ![]() , зависящим от текущего
числа заявок в i-ой системе, i=1,2,3.
, зависящим от текущего
числа заявок в i-ой системе, i=1,2,3.
Заявки поступают из общего потока заявок во второй узел и
первый узел с вероятностями ![]() и
и ![]() соответственно. После
обслуживания во втором узле заявки поступают на третий узел. А после
обслуживания на первом узле заявки поступают с вероятностью
соответственно. После
обслуживания во втором узле заявки поступают на третий узел. А после
обслуживания на первом узле заявки поступают с вероятностью ![]()
![]() в третий узел либо с
вероятностью
в третий узел либо с
вероятностью ![]()
![]() в первый узел, либо с
вероятностью
в первый узел, либо с
вероятностью ![]() в третий узел. После
обслуживания на 3 узле заявки уходят из системы.
в третий узел. После
обслуживания на 3 узле заявки уходят из системы.
2.3 Уравнения равновесия
Предположим, что существует стационарное распределение![]() . Составим уравнение
равновесия.
. Составим уравнение
равновесия.
P![]()
![]()
![]() P
P![]()
![]() +
+![]()
![]() P
P![]()
![]() +
+
+![]()
![]() P
P![]()
![]() +
+![]() P
P![]()
![]() +
+
+![]()
![]() P
P![]()
![]() +
+ ![]()
![]() P
P![]()
![]() +
+
+![]() P
P![]()
2.4 Нахождение стационарных вероятностей
Для того, чтобы найти решение уравнения равновесия ![]() , воспользуемся теоремой 1
из 1.7 из которой получим, что
, воспользуемся теоремой 1
из 1.7 из которой получим, что
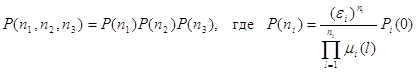 ,
,
![]() -вероятность
поступления заявок в i-ую подсистему.
-вероятность
поступления заявок в i-ую подсистему.
Таким образом, нам необходимо найти ![]() . Для этого воспользуемся
соотношением (3) из 1.7
. Для этого воспользуемся
соотношением (3) из 1.7
Из системы ![]() получим
получим
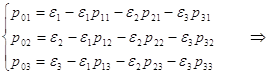 где
где ![]() -вероятности перехода
-вероятности перехода
Матрица перехода имеет вид:
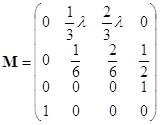
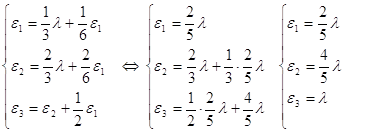
Тогда, получим
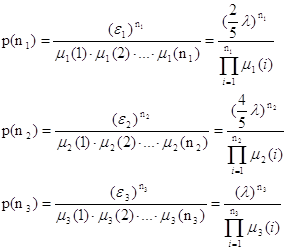
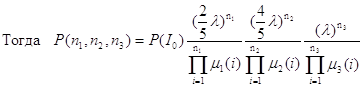
где Io - нулевой вектор.
Итак, стационарное распределение найдено с точностью до постоянного множителя P (Io).
2.5 Условия эргодичности
Для исследования эргодичности применим эргодическую теорему Фостера (теорема 1 из 1.1)
Теорема (Эргодическая теорема Фостера).
Регулярная Марковская цепь с непрерывным временем и счетным числом состояний эргодична, если она неприводима и система уравнений
![]()
имеет нетривиальное решение ![]() такое,
что
такое,
что ![]()
При этом существует единственное стационарное распределение, которое совпадает с эргодическим.
Рассмотрим условия этой теоремы.
Регулярность следует из того, что ![]() . Неприводимость следует из
того, что все состояния сообщаются с нулевым, то есть в любое состояние
. Неприводимость следует из
того, что все состояния сообщаются с нулевым, то есть в любое состояние ![]() можно перейти из нулевого (0,0,0)
путем поступления, перехода, обслуживания заявок.
можно перейти из нулевого (0,0,0)
путем поступления, перехода, обслуживания заявок.
В качестве нетривиального решения системы уравнений из
теоремы Фостера возьмем ![]() . Тогда
для эргодичности потребуется, чтобы
. Тогда
для эргодичности потребуется, чтобы
![]()
Тогда получим,
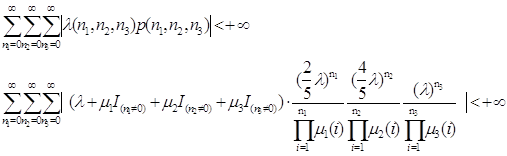
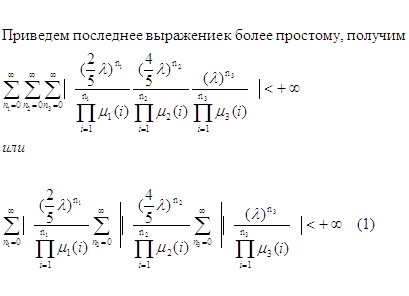
Условие (1) и есть искомое условие эргодичности. Если это условие будет выполнятся, то будет существовать единственное стационарное распределение, совпадающее с эргодическим.
3. Немарковский случай
3.1 Описание модели
Дана модель
открытой сети массового обслуживания, точно такая как марковском случае Только предполагается, что
длительность обслуживания отдельного требования распределена по произвольному
закону. Пусть ![]() - произ. функция
распределения времени обслуживания
- произ. функция
распределения времени обслуживания ![]() -той
заявки в
-той
заявки в ![]() -том узле, при этом
предполагаем, что выполняется следующее требование:
-том узле, при этом
предполагаем, что выполняется следующее требование:
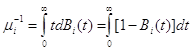 .
.
Состояние сети в момент времени t определяется вектором
![]() , где
, где
![]() - остаточное
время обслуживания заявки, первой подсистемой, стоящей в
- остаточное
время обслуживания заявки, первой подсистемой, стоящей в ![]() -ой позиции.
-ой позиции.
![]() - остаточное
время обслуживания заявки, второй подсистемой, стоящей в
- остаточное
время обслуживания заявки, второй подсистемой, стоящей в ![]() -ой позиции.
-ой позиции.
![]() остаточное время
обслуживания заявки, третьей подсистемой, стоящей в
остаточное время
обслуживания заявки, третьей подсистемой, стоящей в ![]() -ой
позиции.
-ой
позиции.
|
|||
 |
Система LCFS PR.
Заявка, поступающая в ![]() -ый
узел, вытесняет заявку с прибора и начинает обслуживаться. Вытесненная заявка
идет в начало очереди.
-ый
узел, вытесняет заявку с прибора и начинает обслуживаться. Вытесненная заявка
идет в начало очереди.
![]() -
-
не Марковский процесс.
Рассматривается следующий процесс
![]()
![]() - остаточное
время обслуживания заявки, первой подсистемой, стоящей в
- остаточное
время обслуживания заявки, первой подсистемой, стоящей в ![]() -ой позиции.
-ой позиции.
3.2 Составление дифференциально-разностных уравнений
Рассматриваем![]() случайный
процесс
случайный
процесс
![]()
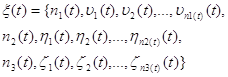
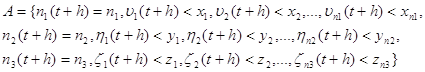
![]()
Где h-некоторый достаточно малый промежуток времени.
Тогда вероятность события А будет равна сумме следующих вероятностей:
1. Если в промежутке времени h в систему не пришло ни одного требования и ни на одном приборе обслуживание не закончилось, то:
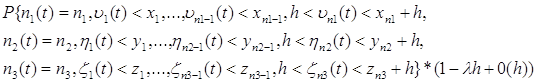
2. Если в промежутке
времени h первая подсистема обслужила одну заявку, и
произошел переход заявки на третью подсистему с вероятностью ![]() , то:
, то:
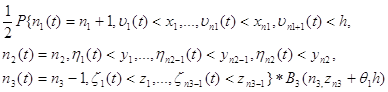
3. Если в промежутке времени h вторая подсистема обслужила одну заявку, то:
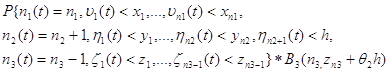
4. Если в промежутке времени h третья подсистема обслужила одну заявку и произошел выход заявки из системы с вероятностью 1, то:
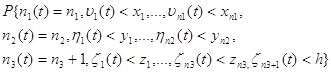
5. Если в промежутке времени h на первую подсистему поступила одна заявка с интенсивностью ![]() , то:
, то:
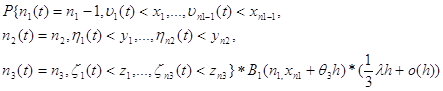
6. Если в промежутке времени h на вторую подсистему поступила одна заявка с интенсивностью ![]() , то:
, то:
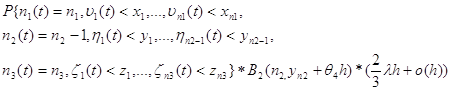
7. Если в промежутке времени h первая подсистема обслужила одну заявку и произошел переход заявки на
вторую подсистему с вероятностью ![]() , то:
, то:
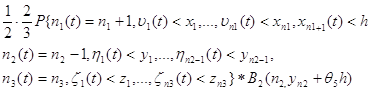
8. Если в промежутке
времени h первая подсистема обслужила одну заявку и произошел переход заявки на
первую подсистему с вероятностью![]()
![]() , то:
, то:
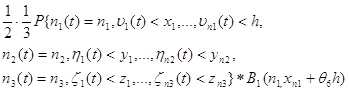
Тогда вероятность события А будет равна сумме данных восьми слагаемых.
Перейдем к функции распределения и составим систему дифференциально-разностных уравнений
(Будем использовать разложение функции распределения в ряд Тейлора)
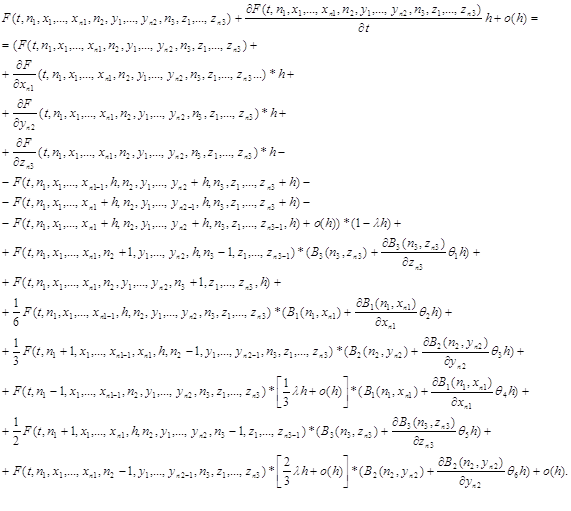
Сократив одинаковые слагаемые, разделим обе части уравнения на h и устремим h к нулю. В результате преобразований мы получим следующую систему.
![]()
![]()
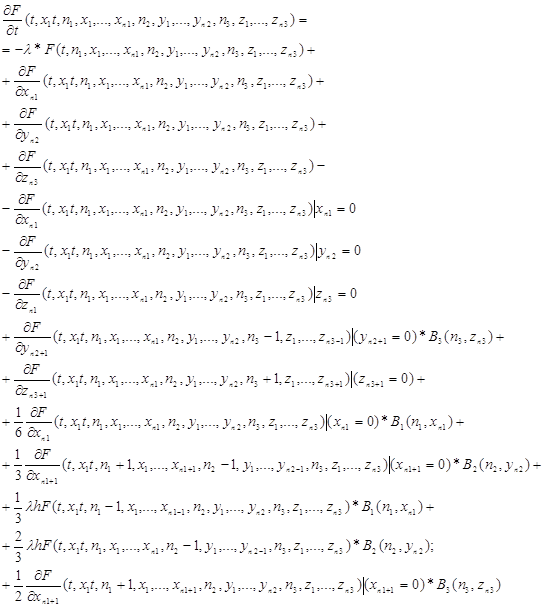
3.3 Поиск решения дифференциально-разностных уравнений
Тогда непосредственной подстановкой можем убедиться, что решением данного уравнения будет.
![]()
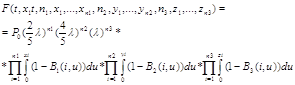
![]()
![]()
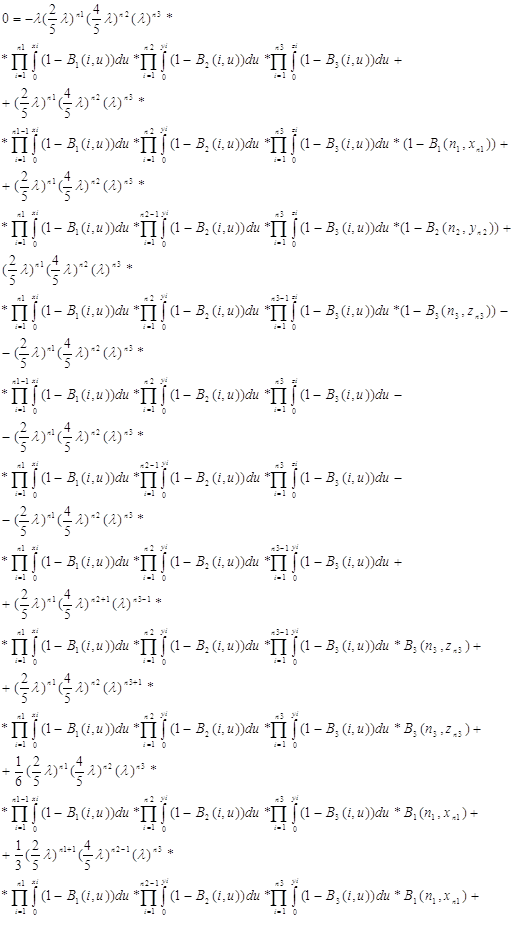
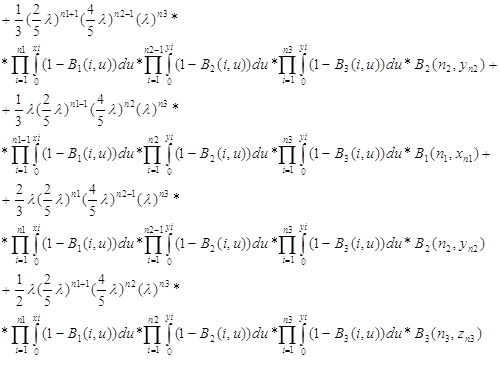
Приводя подобные слагаемые получили, что F-действительно решение этого уравнения. И таким образом
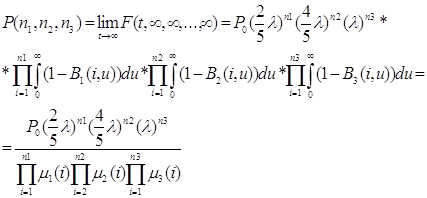
Список литературы
1. Гнеденко Б.В., Коваленко И.Н. Введение в теорию массового обслуживания. М.: Наука, 1966. - 431с.
2. Ширяев А.Н. Вероятность. - М.: Наука, 1980. - 575с.
3. Буриков А.Д., Малинковский Ю.В., Маталыцкий М.А. Теория массового обслуживания: Учебное пособие по спецкурсу. - Гродно, 1984. - 108с. (ГрГу).
4. Феллер В. Введение в теорию вероятностей и её приложения: в 2-х т. М.: Мир, 1967, - т.1,-498с.
5. Кениг Д., Штоян Д. Методы теории массового обслуживания. - М.: Радио и связь, 1981. - 127с.