Контрольная работа: Интегралы. Функции переменных

Вариант 2

I.          Вычислить интегралы

Преобразуем подынтегральное выражения с целью его непосредственного интегрирования:

Найдем А и В:

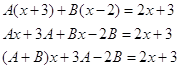
Отсюда видно что А и В являются решением системы:

Решим эту систему и найдем А и В:

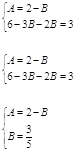
Итак, A=3/5, B=7/5, зная эти коэффициенты, вычисляем интеграл.

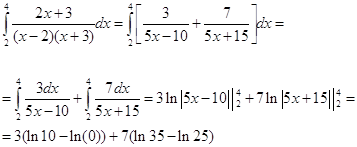
 с помощью замены переменных

Введем  и возьмем соответствующий неопределенный интеграл:

Возвращаемся к x:

Теперь вычисляем определенный интеграл:

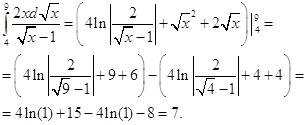
Итак,

3.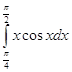 методом интегрирования по частям

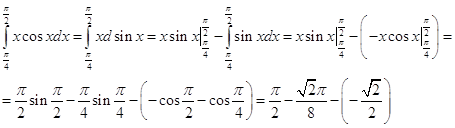
Итак,

II. Функции многих переменных

1. Найти частные производные 1-го порядка

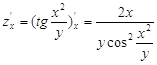
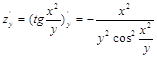
2. Исследовать на экстремум функцию

Найдем частные производные

Найдем все стационарные точки функции, точки в которых должны выполняться условия: ,

Это равносильно следующему:

Вторая система не имеет вещественного корня

t= 0 t=1

y=1 y=-1

x=1

M0(0;0) и M1(1;1) – стационарные точки данной функции.

Теперь определим характер этих стационарных точек.

Найдем частные производные второго порядка этой функции.

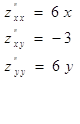
В точке M0(0;0):

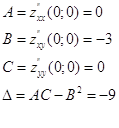
Так как <0, то экстремума в точке M0(0;0) нет.

В точке M1(1;1):

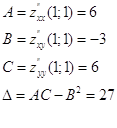
Так как >0,A>0,C>0 то точка M1(1;1) это точка экстремума,

Причем этот экстремум-минимум.

III. Решить дифференциальные уравнения.

1. Решить уравнение с разделяющимися переменными

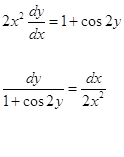
Интегрируем правую и левую части уравнения:

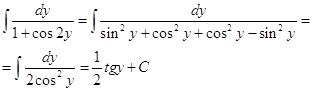
После некоторых преобразований выражаем решение уравнения:

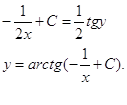
2. Решить линейное уравнение 1-го порядка

Ищем решение уравнения в виде произведения двух функций:

При этом:

После подстановки в исходное уравнение имеем:

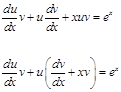
Чтобы коэффициент при u обратился в 0, в качестве v выбираем функцию удовлетворяющую уравнению:

Найдем функцию u, которая должна удовлетворять уравнению:

:

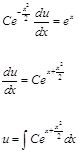Решение запишется в виде:

3

Это неоднородное линейное дифференциальное уравнение второго порядка. Его решение ищем в виде:

, где  - общее решение соответствующего однородного уравнения,  - частное решение.

Найдем

Решим однородное дифференциальное уравнение

Характеристическое уравнение для него:

Это квадратное уравнение

d=36-100=-64 – дискриминант отрицательный, корни комплексные:

k1=3-4i ; k2=3+4i

Общее решение, следовательно, имеет вид:

,

где  - константы.

Ищем частное решение. Функция свободного члена имеет вид:

, где a=2,b=3,k=1,p=-6,q=25

При этом , следовательно, частное решение ищем в виде:

Находим его производные первого и второго порядка и подставляем в уравнение:

Для нахождения коэффициентов А и В решим систему:

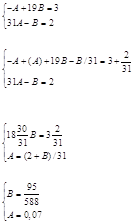
A=0,07, B=0,16

Таким образом, окончательное решение уравнения имеет вид:

IV. Ряды

1.         Исследовать на сходимость ряд с положительными членами

Рассмотрим ряд:

Это степенной ряд с основанием меньшим 1, а он заведомо сходится.

Теперь сравним члены ряда  с членами ряда

 при n>4 , значит ряд  также сходится.

2.         Исследовать на абсолютную и условную сходимость ряд:

Исследуем на абсолютную сходимость (сходимость ряда, состоящего из модулей членов знакопеременного ряда) значит необходимый признак сходимости выполняется.

,

Сравним член этого ряда с членом заведомо расходящегося гармонического ряда:

, следовательно наш ряд расходится абсолютно.

Исследуем ряд на условную сходимость:

Так как условия признака Лейбница выполнены

данный ряд сходится условно.

3. Найти область сходимости функционального ряда

, перепишем его в виде:

Член данного ряда представляет собой член степенного ряда, помноженный на член гармонического ряда.

Для расходящегося гармонического ряда выполняется однако основной признак сходимости (его член стремится к нулю), так что сходимость функционального ряда  определяется сходимостью степенного ряда: , причем при любом x это будет знакопостоянный ряд.

Cтепенной же ряд сходится когда его член по модулю <1:

Решаем это модульное неравенство и находим область сходимости функционального ряда :

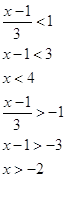
Итак, область сходимости функционального ряда :