Реферат: Интерполирование и приближение функций
Міністерство освіти і науки України
Національний технічний університет
“ХАРКІВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ”
Кафедра “Обчислювальної техніки та програмування”
Реферат з курсу “Численные методы”
Тема: “ИНТЕРПОЛИРОВАНИЕ И ПРИБЛИЖЕНИЕ ФУНКЦИЙ”
Виконав:
Перевірив:
Харків
Содержание
1. Разделенные разности
2. Интерполяционный многочлен Лагранжа
3. Интерполяционный многочлен Ньютона
4. Аппроксимация функций методом наименьших квадратов
Литература
1. Разделенные разности
Часто экспериментальные данные функциональной зависимости представляются таблицей, в которой шаг по независимой переменной не постоянен. Для работы с таким представлением функции конечные разности и конечно-разностные операторы не пригодны. В этом случае первостепенную роль играют разделенные разности.
Разделенную разность
функции f(x) для некоторых двух точек ![]() и
и ![]() определяют следующей дробью:
определяют следующей дробью:
![]()
Для построения степенного многочлена, проходящего через заданные точки, необходимо иметь число точек на единицу больше, чем степень многочлена. Согласно определению разделенной разности число их для n точек равно числу сочетаний из n по 2. Это во много раз больше, чем необходимо для построения кривых, проходящих через n точек. Из опыта работы с конечными разностями видно, что разделенных разностей из всего множества достаточно выбрать всего n, но выбрать так, чтобы в их образование входили все (n+1) точек таблицы.
Вполне разумно вычислять
разделенные разности только для соседних значений функции в таблице. В этом
случае говорят об упорядоченных разделенных разностях. Аргументу табличной
функции присваиваются индексы из чисел натурального ряда, начиная с нуля, в
результате чего обозначения разделенных разностей для i-той строки таблицы
будут ![]() .
.
Повторная разность от разделенной разности есть разделенная разность второго порядка:
![]()
![]()
![]()
В общем случае разделенная разность n-го порядка имеет вид:
![]()
2. Интерполяционный многочлен Лагранжа
Произведения из
скобочных сомножителей в знаменателе каждого слагаемого напоминают своим видом
некий степенной многочлен от переменной ![]() , который своими корнями имеет
значения
, который своими корнями имеет
значения ![]() ,
исключая
,
исключая ![]() .
Многочлен от x с корнями в этих же точках, включая и
.
Многочлен от x с корнями в этих же точках, включая и ![]() , будет иметь вид:
, будет иметь вид:
![]()
Удаляя тот или иной
сомножитель из ![]() , можно по желанию исключить
ненужный нуль многочлена. Если взять i-тое слагаемое без
, можно по желанию исключить
ненужный нуль многочлена. Если взять i-тое слагаемое без ![]() из выражения для
разделенной разности n-го порядка и умножить его на
из выражения для
разделенной разности n-го порядка и умножить его на ![]() , в котором отсутствует
сомножитель
, в котором отсутствует
сомножитель ![]() ,
то многочлен степени n будет обладать следующими свойствами:
,
то многочлен степени n будет обладать следующими свойствами:
![]()
Если умножить ![]() на
на ![]() , то полученный
многочлен степени n будет проходить через точку с координатами
, то полученный
многочлен степени n будет проходить через точку с координатами ![]() и будет равен нулю во
всех точках
и будет равен нулю во
всех точках ![]() .
Сумма таких многочленов по всем
.
Сумма таких многочленов по всем ![]() определяет интерполяционный многочлен
Лагранжа степени n.
определяет интерполяционный многочлен
Лагранжа степени n.
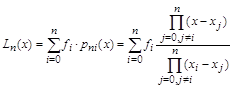 .
.
3. Интерполяционный многочлен Ньютона
Интерполяционный многочлен в форме многочлена Лагранжа не удобен в случаях, когда необходимо добавлять экспериментальные данные в таблицу с целью повышения точности интерполяции. При этом необходимо проводить все вычисления заново.
Если задачу поставить так, что добавление лишней точки требовало бы лишь добавки некоторого многочлена степени (n+1) к многочлену Лагранжа n-й степени, то эту добавку можно искать, выполнив в общем виде преобразование разности двух многочленов Лагранжа: степени (n+1) и n. Несложные преобразования приводят к следующему соотношению для добавочного многочлена степени (n+1):
![]() ,
,
где ![]() – многочлен степени (n+1),
– многочлен степени (n+1),
![]() – разделенная разность (n+1)-го
порядка.
– разделенная разность (n+1)-го
порядка.
Если считать разделенную
разность нулевого порядка равной значению функции ![]() в точке
в точке ![]() , то
, то
![]()
Поступая аналогичным
образом и находя последовательно ![]() , в конце концов, получим общее
выражение для другой формы представления интерполяционного многочлена Лагранжа,
которая в литературе называется интерполяционным многочленом Ньютона для
неравных интервалов и записывается так:
, в конце концов, получим общее
выражение для другой формы представления интерполяционного многочлена Лагранжа,
которая в литературе называется интерполяционным многочленом Ньютона для
неравных интервалов и записывается так:
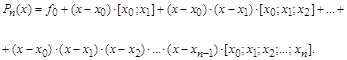
Надо отметить, что дополнительную точку в таблицу необходимо записывать в самую нижнюю строку таблицы, чтобы не нарушить уже имеющегося упорядочения разностей и ускорить вычисление новых.
И, наконец, надо отметить, что и многочлен Лагранжа, и многочлен Ньютона удобны для вычислений, но после раскрытия скобок и приведения подобных дают один и тот же степенной многочлен.
4. Аппроксимация функций методом наименьших квадратов
Основным недостатком интерполяционных
многочленов является наличие у них большого числа экстремумов и точек
перегибов, что определяется суммированием в них многочленов ![]() , n раз меняющих свой
знак. Кроме того, исходные табличные значения функции заданы неточно по разным
причинам, поэтому строить многочлены выше 4-5-й степени, зная, что из
теоретических исследований функция в интервале таблицы совсем не такая, не
имеет особого смысла.
, n раз меняющих свой
знак. Кроме того, исходные табличные значения функции заданы неточно по разным
причинам, поэтому строить многочлены выше 4-5-й степени, зная, что из
теоретических исследований функция в интервале таблицы совсем не такая, не
имеет особого смысла.
Если табличные значения функции можно интерпретировать как теоретическое значение плюс погрешность, то, задав некоторый критерий близости теоретической кривой к заданному множеству табличных точек, можно найти нужное число параметров этой кривой.
Наиболее популярным критерием близости является минимум среднего квадрата отклонения:
![]() ,
,
где ![]() – точка
экспериментальных данных из таблицы,
– точка
экспериментальных данных из таблицы,
![]() – значение искомой зависимости в
точке
– значение искомой зависимости в
точке ![]() .
.
Если искомую зависимость желательно представить многочленом степени n, то (n+1) коэффициент в нем будут представлять неизвестные параметры. Подставив в сумму квадратов отклонений искомый многочлен, получим функционал, зависящий от этих параметров:
![]()
Чтобы функционал ![]() был минимален,
необходимо все частные производные функционала по параметрам приравнять нулю и
систему разрешить относительно неизвестных параметров
был минимален,
необходимо все частные производные функционала по параметрам приравнять нулю и
систему разрешить относительно неизвестных параметров ![]() . Эти действия приводят к
следующей системе линейных уравнений
. Эти действия приводят к
следующей системе линейных уравнений
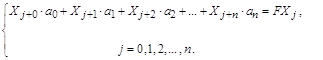
Здесь ![]() – постоянный
коэффициент, равный сумме (j+k)-тых степеней всех значений аргументов. Для их
ручного вычисления удобно к исходной таблице данных добавить еще
– постоянный
коэффициент, равный сумме (j+k)-тых степеней всех значений аргументов. Для их
ручного вычисления удобно к исходной таблице данных добавить еще ![]() столбцов.
столбцов. ![]() – числовые
значения в правой части системы линейных алгебраических уравнений, для подсчета
которых тоже
– числовые
значения в правой части системы линейных алгебраических уравнений, для подсчета
которых тоже
удобно к исходной таблице данных добавить еще n столбцов.
Демонстрацию метода
наименьших квадратов проведем для данных с количеством точек в таблице, равным
4. Максимальная степень аппроксимирующего многочлена для такого набора равна 3,
так как должно выполняться соотношение: ![]() . Для максимальной степени аппроксимирующий
и интерполяционный многочлены равны.
. Для максимальной степени аппроксимирующий
и интерполяционный многочлены равны.
Пусть таблица данных после добавления в нее дополнительных колонок выглядит следующим образом:
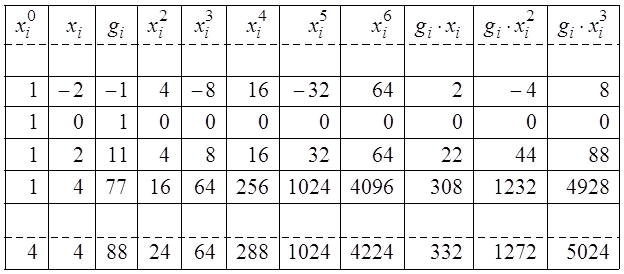
В нижней строке размещаем итоговые суммы по каждой колонке.
Система уравнений для полинома третьей степени:
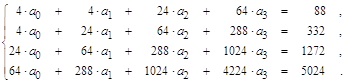
Решив систему, найдем: ![]()
![]()
Эта же таблица без
добавления чего-либо позволяет найти коэффициенты аппроксимирующего многочлена
второй степени. Для этого достаточно в системе для полинома третьей степени
убрать 4-е уравнение, а из остальных уравнений исключить слагаемые с
неизвестной ![]() .
В результате система уравнений для полинома второй степени будет:
.
В результате система уравнений для полинома второй степени будет:
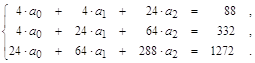
Решив систему, найдем: ![]()
![]()
Аналогично можно уменьшать число уравнений для построения аппроксимирующих многочленов первой и нулевой степеней.
На рисунке 1 показаны графики двух аппроксимирующих многочленов второй и третьей степени. Многочлен третьей степени проходит через 4 заданные точки, а многочлен второй степени проходит сквозь множество заданных точек с минимумом суммы квадратов отклонений от них, что хорошо видно на графиках.
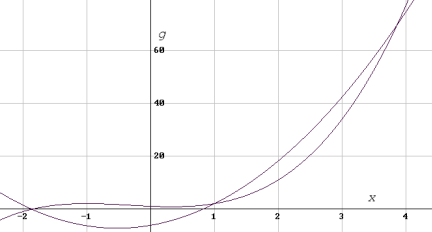
Рисунок 1.
Литература
1. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы: Учеб. пособие. – М.: Наука, 1987. – 600 с.
2. Воеводин В.В. Численные методы алгебры. Теория и алгорифмы. - М.: Наука, 1966. – 248 с.
3. Воеводин В.В. Вычислительные основы линейной алгебры. – М.: Наука, 1977. – 304 с.
4. Волков Е.А. Численные методы. – М.: Наука, 1987. – 248 с.
5. Калашников В. И. Аналоговые и гибридные вычислительные устройства: Учеб. пособие. – Харьков: НТУ “ХПИ”, 2002. – 196 с.
6. Вержбицкий, В. М. Численные методы. Математический анализ и обыкновенные дифференциальные уравнения. М.: Высш.шк., 2001. 383 с.
7. Волков, Е. А. Численные методы. СПб.: Лань, 2004. 248 с.
8. Мудров, А. Е. Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль. Томск: МП "РАСКО", 1991. 272 с.
9. Шуп, Т. Е. Прикладные численные методы в физике и технике. М.: Высш. шк., 1990. 255 с.
10. Бахвалов, Н. С. Численные методы в задачах и упражнениях / Н. С. Бахвалов, А. В. Лапин, Е. В. Чижонков. М.: Высш. шк., 2000. 192 с.
| Численные методы решения типовых математических задач | |
|
... УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ Тульский государственный университет Кафедра автоматики и телемеханики Численные методы решения ... Интерполяционный многочлен может быть построен при помощи специальных интерполяционных формул Лагранжа, Ньютона, Стерлинга, Бесселя и др. Лемма: алгебраический многочлен (2.2), построенный по формулам Ньютона, действительно является интерполяционным многочленом, т.е. значение многочлена в узловых точках равно ... |
Раздел: Рефераты по математике Тип: курсовая работа |
| Математический анализ | |
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ "ХПИ" Кафедра "Вычислительной техники и програмирования" Расчётно ... Получить интерполяционные многочлены Лагранжа и Ньютона, проходящие через первые четыре точки таблично заданной функции G(x), и сравнить их степенные представления. Проведем проверку вычислений, подставив x=0.8 в интерполяционный многочлен Лагранжа, получим y1=0.604 |
Раздел: Рефераты по математике Тип: контрольная работа |
| Методика формирования умений решать тригонометрические уравнения и ... | |
|
Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования "Поморский государственный ... Использование указанных приемов приводит к тригонометрическим уравнениям, которые условно можно разделить на следующие виды: В-четвертых, целесообразно провести работу по актуализации у учащихся приемов преобразования суммы (разности) тригонометрических функций в произведение, обратить внимание ... |
Раздел: Рефераты по математике Тип: дипломная работа |
| Самостоятельная работа как средство обучения решению уравнений в 5-9 ... | |
|
... РФ Светлоградский педагогический колледж Дипломная работа Самостоятельная работа как средство обучения решению уравнений в 5 - 9 классах Выполнила: "Алгебраическое уравнение от одного неизвестного называется уравнением первой степени, если обе его части являются многочленами первой степени относительно неизвестного". В ряде учебников, кроме основной формулы для корней квадратного уравнения ах2 + bх + с = 0, приводятся еще формулы корней уравнения x2+px+q=0 или x2+2px+q=0. Иногда использование ... |
Раздел: Рефераты по педагогике Тип: реферат |
| Корни многочленов от одной переменной | |
|
Новосибирский государственный педагогический университет. Математический факультет. Кафедра алгебры. Курсовая работа по математике. Многочлены ... Разделить с остатком многочлен f (x) на ненулевой многочлен g (x) - это значит представить f (x) в виде f (x) =g (x) s (x) +r (x), где s (x) и r (x) -многочлены и либо r (x) =0 ... Многочлен f (x) обладает следующим свойством: для некоторой арифметической прогрессии значения х с разностью, отличной от нуля, соответствующее значение многочлена так же образует ... |
Раздел: Рефераты по математике Тип: курсовая работа |