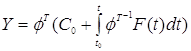Курсовая работа: Исследование методов решения системы дифференциальных уравнений с постоянной матрицей
Содержание
1. Введение
2. Постановка задачи
3. Нахождение собственных чисел и построение ФСР
6. Построение общего решения матричным методом
7. Задача Коши для матричного метода
8. Решение неоднородной системы
Графики
Заключение
1. Введение
Рассмотрим систему линейных уравнений первого порядка, записанную в нормальной форме:
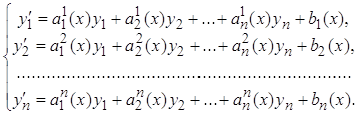 (1)
(1)
где коэффициенты аij , i=1,2,…..,n, к=1,2,…,n, являются постоянными величинами;
yi=yi(t), i=1,2,…,n - неизвестные функции переменной t.
Если все bi(t) (i=1,2,…,n) положить равным нулю (bi(t)=0), то получится однородная система, соответствующая неоднородной системе (1).
Обозначая матрицу системы
через А(х), а вектор ![]() через
через ![]() тогда систему (1) можем
переписать в матричной форме
тогда систему (1) можем
переписать в матричной форме
![]() (1а)
(1а)
Если ![]() , то получаем
соответствующую систему однородных уравнений
, то получаем
соответствующую систему однородных уравнений
![]() . (2)
. (2)
Всякая совокупность n функций
![]()
![]()
![]()
определенных и непрерывно дифференцируемых в интервале (a;b), называется решением системы (1) в этом интервале, если она обращает все уравнения системы (1) в тождества:
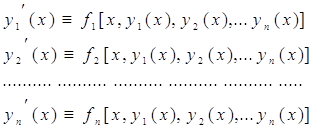
![]()
справедливые при всех значениях x из интервала (a, b). Общее решение неоднородной системы представляет собой сумму общего решения соответствующей однородной системы и частного решения неоднородной.
2. Постановка задачи
Цель работы: исследование методов решения системы дифференциальных уравнений с постоянной матрицей:
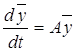 ;
;![]() ;
;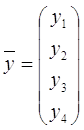
1. Найти собственные числа и построить фундаментальную систему решений (ФСР).
2. Построить фундаментальную матрицу методом Эйлера.
3. Найти приближенное решение в виде матричного ряда.
4. Построить общее решение матричным методом. Исследовать зависимость Жордановой формы матрицы А от ее собственных чисел.
5. Решить задачу Коши.
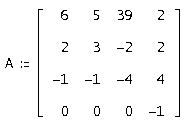
Начальные условия:
Вектор начальных условий: [1, 2, 3, 4]
t = 0
3. Нахождение собственных чисел и построение ФСР
Однородной линейной системой дифференциальных уравнений называется система уравнений вида:
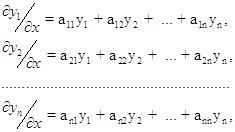 (3)
(3)
Если в матрице системы ![]() все
все ![]() =const,
то данная система называется системой с постоянными коэффициентами или с
постоянной матрицей.
=const,
то данная система называется системой с постоянными коэффициентами или с
постоянной матрицей.
Фундаментальной системой решений однородной линейной системы уравнений называется базис линейного пространства решений a, т.е. n линейно независимых решений этой системы.
Для построения фундаментальной системы решений дифференциального уравнения необходимо найти собственные числа характеристического полинома, так как в зависимости от их вида (характеристические числа могут быть действительными разными, кратными, комплексными) строится фундаментальная система решений.
Для того чтобы эта система n линейных однородных уравнений с n неизвестными имела нетривиальное решение, необходимо и достаточно, чтобы определитель системы (вронскиан) был равен нулю:
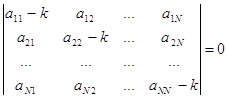 (4)
(4)
Из этого уравнения степени n определяется значение k, при которых система имеет нетривиальные решения. Уравнение (4) называется характеристическим.
Запишем характеристический полином, для этого воспользуемся функцией CHARPOLY
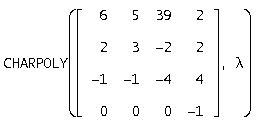
![]()
Для нахождения собственных чисел воспользуемся функцией SOLVE(U, l), которая возвращает характеристические числа матрицы А в вектор l. Получим:
![]()
![]()
Получилось два действительно корня ![]() и два
комплексно-сопряженных корня
и два
комплексно-сопряженных корня ![]() . Следовательно, вектора,
образующие фундаментальную матрицу, для данного типа корней будут находиться
отдельно для
. Следовательно, вектора,
образующие фундаментальную матрицу, для данного типа корней будут находиться
отдельно для ![]() и отдельно для
и отдельно для ![]() . Запишем ФСР для данных
для полученных характеристических чисел:
. Запишем ФСР для данных
для полученных характеристических чисел:
Матрицу y(x), столбцами которой являются решения, образующие фундаментальную систему, называют фундаментальной матрицей.
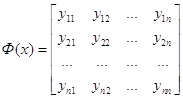
И общее решение системы будет выглядеть следующим образом:
![]()
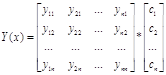
Найдем решение данной системы с помощью метода Эйлера.
4. Построение фундаментальной матрицы решений методом Эйлера
Метод Эйлера заключается в следующем.
Решение системы (1) находится в виде:
![]() (5)
(5)
Функция (5) является решением системы
(1), если ![]() –
собственное значение матрицы А, а а – собственный вектор этой матрицы,
соответствующей числу
–
собственное значение матрицы А, а а – собственный вектор этой матрицы,
соответствующей числу ![]() . Если собственные значения
. Если собственные значения ![]() 1,
1, ![]() 2, …
,
2, …
,![]() n матрицы А попарно различны и a1, a2, …, an соответствующие собственные векторы
этой матрицы, то общее решение системы уравнений (1) определяется формулой :
n матрицы А попарно различны и a1, a2, …, an соответствующие собственные векторы
этой матрицы, то общее решение системы уравнений (1) определяется формулой :
![]()
где С1, С2, … , Сn – произвольные числа.
Для случая кратных корней решение системы принимает вид
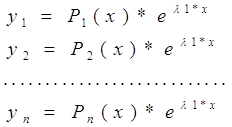 (6)
(6)
где Pi(x)-полиномы степени не выше, чем (к-1), имеющих в совокупности к произвольных коэффициентов. Так что среди коэффициентов этих полиномов к коэффициентов являются произвольными, а оставшиеся к·n-k выражаются через них. Для отыскания коэффициентов полиномов подставим решение (6) в исходную систему уравнений, приравняем коэффициенты при одинаковых функциях. Решим систему по отношению к (k·n-k) коэффициентов. Получим выражение всех коэффициентов через свободные.
Если для кратного собственного
значения ![]() матрицы
А имеется столько линейно независимых собственных векторов
матрицы
А имеется столько линейно независимых собственных векторов ![]() , какова его кратность,
то ему соответствует k
независимых решений исходной системы:
, какова его кратность,
то ему соответствует k
независимых решений исходной системы:
![]()
Если для собственного значения ![]() кратности k имеется только m (m<k)
линейно независимых собственных векторов, то решения, соответствующие
кратности k имеется только m (m<k)
линейно независимых собственных векторов, то решения, соответствующие ![]() , можно искать
в виде произведения векторного многочлена степени k - m на
, можно искать
в виде произведения векторного многочлена степени k - m на ![]() , т.е. в виде:
, т.е. в виде:
![]()
Чтобы найти векторы ![]() , надо подставить выражение (4) в систему (3).
Приравняв коэффициенты подобных членов в левой и правой частях системы, получим
уравнение для нахождения векторов
, надо подставить выражение (4) в систему (3).
Приравняв коэффициенты подобных членов в левой и правой частях системы, получим
уравнение для нахождения векторов ![]() .
.
Для данного задания были найдены следующие собственные значения:
![]() .
.
Построили фундаментальную систему решений:
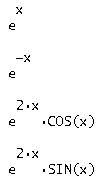
Найдем 1 строку фундаментальной
матрицы решений для характеристического числа ![]() . Запишем третью строку решений в
общем виде:
. Запишем третью строку решений в
общем виде:
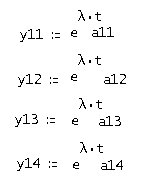
Где аij найдем по выражению:
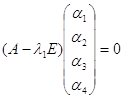 или
или 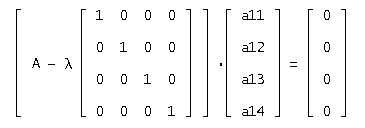
Полученная матрица:
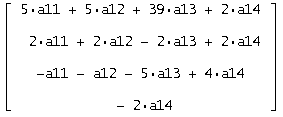
Решаем систему:
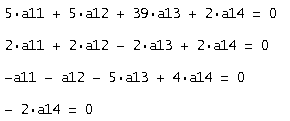
Полученные корни:
![]()
Доопределим ![]()
Тогда первая строка будет иметь вид:
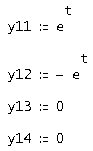
Аналогично найдем вторую строку фундаментальной матрицы решений для первого характеристического числа -1. Полученные значения:
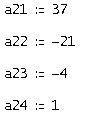
Тогда вторая строка будет иметь вид:
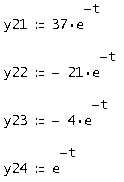
Найдем третью и четвертую
строки фундаментальной матрицы решений для первого характеристического числа ![]() . Сопряженный
корень
. Сопряженный
корень![]() не
порождает новых вещественных линейно независимых частных решений.
не
порождает новых вещественных линейно независимых частных решений.
Полученные значения:
![]()
Отделяя в нем вещественные и мнимые части, получим два вещественных решения, которые и составляют первую и вторую строки фундаментальной матрицы решений
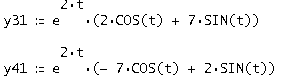
Аналогично остальные 3:
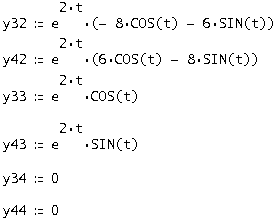
Запишем найденную фундаментальную матрицу решений:
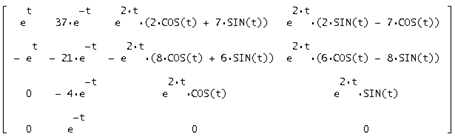
Умножим транспонированную
фундаментальную матрицу решений на вектор свободных коэффициентов ![]() и получим
вектор общего решения исходной системы:
и получим
вектор общего решения исходной системы:
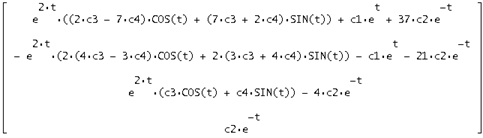
Сделаем проверку найденного решения следующим образом:
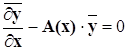
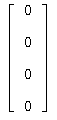
Получаем нулевую матрицу-столбец:
 что
показывает, что общее решение найдено верно.
что
показывает, что общее решение найдено верно.
5. Нахождение приближённого решения в виде матричного ряда
Дадим определение матричному ряду и экспоненциальной функции матрицы.
Матричные ряды.
Рассмотрим бесконечную последовательность матриц ![]() ,
, ![]() ,
,![]() . Будем говорить, что
последовательность матриц сходится к матрице А:
. Будем говорить, что
последовательность матриц сходится к матрице А:
![]() ,
,
если ![]() при
при ![]() . Из определения нормы
следует, что сходимость матриц эквивалентна поэлементной сходимости. Матричным
рядом называется символ
. Из определения нормы
следует, что сходимость матриц эквивалентна поэлементной сходимости. Матричным
рядом называется символ ![]() , причем говорят, что этот ряд
сходится к сумме
, причем говорят, что этот ряд
сходится к сумме ![]() , если к f сходится последовательность частичных сумм Sk, где
, если к f сходится последовательность частичных сумм Sk, где
. ![]()
Пусть ![]() , тогда можно определить
степень матрицы А обычным образом:
, тогда можно определить
степень матрицы А обычным образом:
![]() (k раз).
(k раз).
Рассмотрим ряд, называемый степенным:
![]() ,
, ![]() ,
, ![]() ,
,
где по определению положим A0 = En.
Экспоненциальная функция матрицы. В качестве примера рассмотрим степенной ряд, равный:
![]() .
.
Так как радиус сходимости соответствующего числового ряда
![]()
Равен бесконечности, то ряд сходится при всех А. Сумма ряда называется экспоненциальной функцией (экспонентой) и обозначается через еА, если ехр{А}.
Приближенно вектор решений можно найти как произведение матричного ряда:
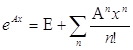
и вектора начальных условий y0=[y1,y2, …..yk].
Формула является матричной задачей Коши в приближенном виде.
Экспонентой ![]() матрицы А
называется сумма ряда
матрицы А
называется сумма ряда
![]()
где Е – единичная матрица.
Матрица ![]() является решением
матричной задачи Коши:
является решением
матричной задачи Коши:
![]() т.е. является фундаментальной
матрицей системы.
т.е. является фундаментальной
матрицей системы.
Найдем разложение матричного ряда последовательно по семи, восьми и десяти первым членам.
для получения разложения по 7 первым членам (аналогично по 8,10 и 10). Результатом будет являться матрица 4*4. Полученные матрицы умножаем на вектор начальных условий S=[1,2,3,4] и получаем приближенное решение в виде матричного ряда.




При увеличении членов разложения ряда вектор приближенных решений будет стремиться к вектору точных решений. Этот факт можно наблюдать, графически сравнивая изображение точного и приближенного решений (см. приложение).
Умножим на соответствующий вектор начальных условий и получим приближенное решение в виде матричного ряда, запишем полученное решение для n=7.
[s1 ≔ 1, s2 ≔ 2, s3 ≔ 3, s4 ≔ 4]

6. Построение общего решения матричным методом
Матричный метод решения системы уравнений (1) основан на непосредственном отыскании фундаментальной матрицы этой системы.
![]()
Экспонентой eA матрицы А называется сумма ряда
где Е – единичная матрица.
Свойство матричной экспоненты:
а) если АВ=ВА, то еА+В=еА*еВ= еВ *еА;
б) если А=S-1*B*S, то еА=S-1*eB*S, где матрица S – это матрица преобразования переменных из собственного базиса в базис исходных переменных.
в) матрица y(t)=eAt является решением матричной задачи Коши:
т.е. является фундаментальной матрицей системы (1).
Из свойства в) следует, что решение y(t) системы (1) удовлетворяющее условию y(0)=y0, определяется выражением y(t)=eAt*y0. Таким образом, задача нахождения решений системы уравнений (1) эквивалентна задачи отыскания матрицы eAt по матрице А.
Для вычисления матрицы eAt удобно представить матрицу А в виде:
![]() ,
,
где матрица S – это матрица преобразования переменных из собственного базиса в базис исходных переменных, а BА – жорданова форма матрицы А, т.к. eAt = S-1*eBt*S.
Жорданова форма матрицы зависит от вида характеристических чисел.
1. Пусть характеристические числа действительные кратные, тогда Жорданова форма матрицы размерности nxn имеет вид:
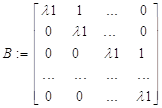
где ![]() - действительный корень кратности n.
- действительный корень кратности n.
2. Если среди корней характеристического полинома имеются, как действительные разные, так и действительные кратные корни, то матрица В имеет вид:
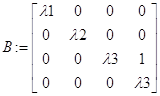
где ![]() - действительные разные корни, а
- действительные разные корни, а ![]() -
действительный корень кратности 2.
-
действительный корень кратности 2.
3. При наличии среди корней характеристического полинома корней комплексно-сопряженных Жорданова клетка выглядит следующим образом:
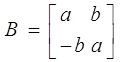
где а ![]() комплексно сопряженный корень
характеристического полинома.
комплексно сопряженный корень
характеристического полинома.
Так как в нашем случае среди характеристических чисел присутствуют, как комплексно-сопряженные корни л = 2 - ∨ л = 2 + , так и действительный разные корни л = -1 ∨ л = 1,то жорданова матрица выглядит следующим образом:
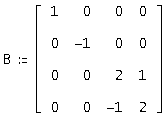
Из уравнения A*S = S*В, где S – невырожденная матрица, получаем систему 16-го порядка, из которой находим элементы матрицы S. Полученная матрица S будет выглядеть следующим образом:

Решаем систему 16-го порядка из уравнения A*S = S*В

Доопределяем некоторые элементы и получаем следующую матрицу S:

Сделаем проверку A*S - S*В=0:
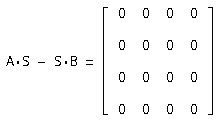
Значит матрица перехода найдена верно.
Для нахождения вектора решений y необходимо умножить матрицу S на ![]() , где
, где ![]() - это вектор, элементы которого
зависят от корней характеристического многочлена:
- это вектор, элементы которого
зависят от корней характеристического многочлена:
![]()
Для комплексных чисел ![]() имеет следующий вид:
имеет следующий вид:
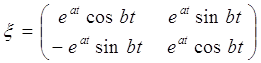
Для случая корней действительных разных:
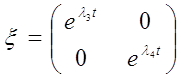
В нашем случае ![]() получается равной:
получается равной:
![]() =
=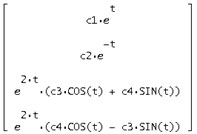
Отсюда найдем общее решение у=S*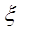 , получим:
, получим:
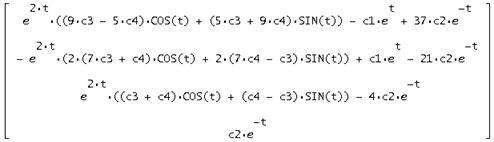
При подстановке решения в исходную систему получается верное равенство, из этого следует, что решение найдено верно:
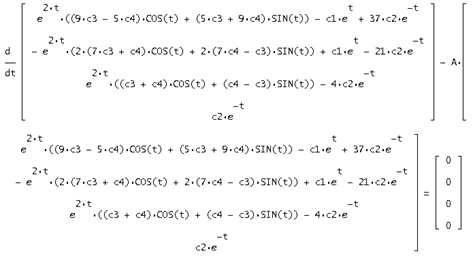
7. Задача Коши для матричного метода
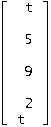
Необходимо из всех решений системы уравнений найти такое решение, в котором y(i)(t) принимает заданное числовое значение y0i в заданной точке, т.е. найти значения сi для следующих заданных значений: x=0, y=[1, 2, 3,4].
В вектор решений y(t) подставляем заданные условия и решаем полученную систему относительно c1, c2, c3, c4 :
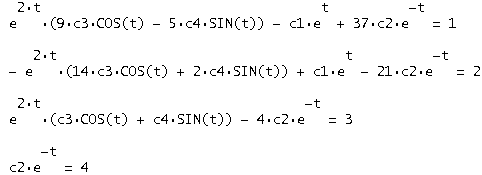
В результате получаем:
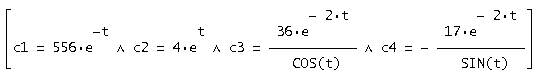
При подстановке c1, c2, c3, c4 в общее решение получим решение в форме Коши:
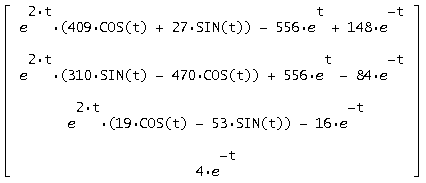
Сделаем проверку, подставив общее решение в исходную систему

Получился нулевой вектор ![]() .
Следовательно, найденная матрица является решением исходной системы.
.
Следовательно, найденная матрица является решением исходной системы.
Исследование зависимости жордановой формы матрицы А от свойств матрицы системы
Пусть J – жорданова клетка матрицы А. Для случая действительных разных корней жорданова клетка будет выглядеть следующим образом:
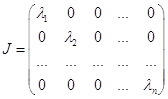
Пусть среди действительных собственных чисел матрицы А есть кратные. Жорданова клетка будет находиться по следующей формуле:
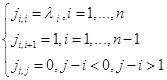
Например, если кратность k=2, то жорданову клетку матрицы мы можем записать так:
![]()
Если кратность k=3, то жорданову клетку матрицы мы можем записать так:
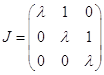
Если же среди трех собственных чисел ![]() являются корнями кратности 2, то
жорданова форма будет выглядеть следующим образом:
являются корнями кратности 2, то
жорданова форма будет выглядеть следующим образом:
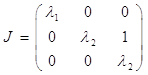
Если два собственных числа матрицы А являются комплексными сопряженными, то запись жордановой клетки будет выглядеть так:
![]()
где ![]() – действительная,
– действительная, ![]() – мнимая часть
собственного числа
– мнимая часть
собственного числа ![]() .
.
8. Решение неоднородной системы
Общее решение неоднородной системы можно найти по формуле:
Где ![]() - фср, Со – матрица
- фср, Со – матрица 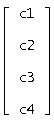 , F(t) – вектор правых части.
, F(t) – вектор правых части.
![]() - общее решение однородной
системы
- общее решение однородной
системы
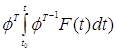 - частное решение неоднородной
системы
- частное решение неоднородной
системы
Полученное частное решение неоднородной системы:
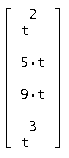
Общее решение однородной системы
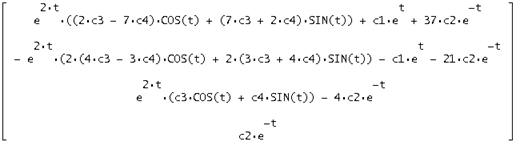
Тогда их сумма будет искомым общим решением неоднородной системы:
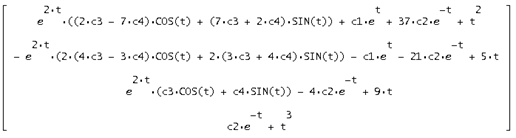
Проверим

Найденное решение верно.
Графики
Изобразим графически точное частное решение однородной линейной системы дифференциальных уравнений с постоянными коэффициентами для начальных условий: t0 = 0, y0 = [1, 2, 3, 4].
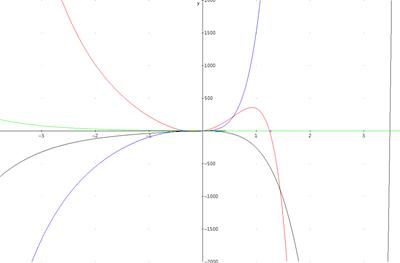
Сравним график одной функции вектора точного решения и одной функции вектора приближенного решения с 3-мя, 5-ю и 7-ю членами ряда:
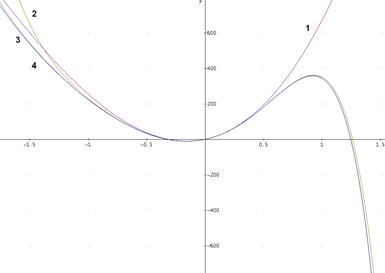
Где 1 – график приближенного решения для трех членов ряда; 2 – график приближенного решения для шести членов ряда; 3 – график приближенного решения для девяти членов ряда; 4 – график точного решения.
Можно сделать вывод:
С увеличением числа членов ряда, число совпадения членов ряда с точным решением будет увеличиваться, область совпадения будет расти.
Заключение
В ходе проделанной работы было изучено 3 метода нахождения общего решения однородной системы линейных дифференциальных уравнений: метод Эйлера, решение в виде матричного ряда и матричный метод. По сравнению с методом Эйлера и матричным методом, метод разложения в матричный ряд прост в реализации, но дает приближенное решение. Также была изучена задача Коши, которая была использована для нахождения частного решения однородной системы линейных дифференциальных уравнений для данного вида начальных условий.
Для установления правильности проведенных вычислений была проведена проверка с помощью подстановки полученных решений в исходную систему уравнений.
Для реализации этой работы в DERIVE были использованы следующие функции пакета:
1.
EIGENVALUES (A, ![]() ) – вычисление собственных чисел
матрицы A с последующей записью в вектор
) – вычисление собственных чисел
матрицы A с последующей записью в вектор ![]() .
.
2.
SOLVE (Pm=0, ![]() ) – решение уравнения Pm=0, где Pm – полином степени m: Pm=p0*
) – решение уравнения Pm=0, где Pm – полином степени m: Pm=p0*![]() m p1*
m p1*![]() m-1+…+pm-1*
m-1+…+pm-1*![]() +pm, а
+pm, а ![]() - переменная, относительно которой решается данное
уравнение.
- переменная, относительно которой решается данное
уравнение.
3.
EXACT_VECTOR(A, ![]() ) – вычисление точного собственного вектора матрицы А
и размещение этих значений в
) – вычисление точного собственного вектора матрицы А
и размещение этих значений в ![]() .
.
4. DIF(A,x,n) – дифференцирование A по x n раз.
5. SUM(M,n,f,g) – вычисление суммы M по n изменяющимся с f до g.
6. VECTOR(u,k,n)– задание (вычисление) вектора значений при k изменяющемся от 1 до n.
А также функции меню:
1. SOLVE/SYSTEM –решение системы с последующим заданием в диалоговом окне количества уравнений, самих уравнений и переменных, относительно которых решается данное уравнение.
2. Simplify > Expand– раскрытие выражений.
Команда Expand используется для раскрытия математических выражений.
Expand expression: #n: где n – номер строки выражения (операнда).
Expand Variable: #n .
В этом варианте команды необходимо указать имя переменной, по которой будет проведено преобразование. Если по всем -<Enter>.
3. Для построения графиков использовали функцию 2D-plot.