Курсовая работа: Інженерна графіка
Інженерна графіка
1. Основні вимоги до виконання та оформлення технічної документації
1.1 Формати креслення (ГОСТ 1.301–68)
Уся технічна документація виконується на аркушах певних розмірів – форматах. Розміри та позначення основних та допоміжних форматів встановлює ГОСТ 1.301–68 «Формати».
ГОСТ 1.301–68 встановлює п’ять основних форматів: А0, А1, А1, А3, А4, розміри яких наведені у таблиці 1.1. ГОСТ 1.301–68 допускає застосування формату А5, розміри якого дорівнюють 148х110.
Таблиця 1.1 – Позначення та розміри основних форматів
| Позначення формату |
А0 |
А1 |
А1 |
А3 |
А4 |
|
Розміри сторін, мм |
1189х841 | 594х841 | 594х410 | 197х410 | 197х110 |
Усі основні формати, крім формату А4, можна розміщати і горизонтально, і вертикально (рис. 1.1б та в). Формат А4 розміщають лише вертикально (рис. 1.1а).

а) б) в)
Рисунок 1.1 – Розміщення основного напису на форматі креслення
На форматі А4 основний напис виконують по його довжині (на короткому боці формату). На усіх інших форматах основний напис виконують у правому нижньому куті формату (рис. 1.1.б та в).
Допоміжна графа основного напису при горизонтальному розміщені формату виконується у лівому верхньому куті, а при вертикальному розміщені формату – у правому верхньому куті вертикально. На рисунку 1.1 наведені приклади розміщення на форматі основного напису та допоміжної графи основного напису при різних орієнтаціях основних форматів. На рисунку 1.1 а наведений формат А4, на рисунку 1.1 б та в різні орієнтації формату А3 та будь-якого більшого формату.
Масштаби зображень (ГОСТ 1.301–68)
Креслення, на яких зображення виконані у натуральну величину, дають правильне уявлення про розміри деталі. Але при великих розмірах деталі виникає необхідність зменшити її або збільшити її при малих розмірах самої деталі, тобто виникає необхідність виконувати зображення на кресленнях у масштабі.
Масштабом називають відношення лінійних розмірів зображення деталі до їх дійсних розмірів. Масштаб креслення повинен відповідати вимогам ГОСТ 1.301–68. Стандартні значення масштабів наведені у таблиці 1.1.
Таблиця 1.1 – Масштаби зображення (ГОСТ 1.301–68)
|
Виконане зображення |
Масштаб зображення |
| У натуральну величину | 1: 1 |
| Із зменшенням | 1:1; 1:1,5; 1:4; 1:5; 1:10; 1:15; 1:10; 1:15; 1:40; 1:50; 1:75; 1:100 |
| Із збільшенням | 1:1; 1,5:1; 4:1; 5:1; 10:1; 10:1; 40:1; 50:1; 100:1 |
Масштаб зображення записують у відповідній графі основного напису креслення (рис. 1.1).

Рисунок 1.1 – Позначення масштабу
Якщо деякі зображення креслення виконані у масштабі, який не збігається з масштабом, зазначеним в основному написі креслення, його записують у дужках поряд із позначенням виконаного нижче зображення. Приклади позначення виглядів та розрізів, виконаних у масштабах, які не збігаються з масштабом, зазначеним у основному написі, наведені на рисунку 1.3.

Рисунок 1.3 – Позначення масштабу на кресленні
У всіх випадках незалежно від масштабу зображень на кресленні повинні бути нанесені дійсні розміри елементів деталі.
Зображення на кресленнях виконуються різними типами ліній, які відрізняються одна від одної кресленням та товщиною (рисунок 1.4).

Рисунок 1.4 – Лінії креслення
ГОСТ 1.303–68 встановлює вимоги до креслення, розмірів та товщини ліній креслення, які зведені у таблицю 1.3. З таблиці зрозуміло, що товщини ліній на кресленні залежать від вибраної товщини суцільної товстої основної лінії (S), яка встановлена у межах від 0,5 до 1,4 мм.
Суцільна товста основна лінія використовується для зображення ліній видимого контуру.
Суцільною тонкою лінією на кресленні виконують лінії виносні та розмірні, лінії штрихування тощо.
Суцільну хвилясту лінію використовують для позначення на кресленні обривань, суцільну тонку зі зламами використовують для позначення значних обривань.
Штрихова лінія використовується для зображення ліній невидимого контуру.
Штрихпунктирною лінією виконують лінії осьові та центрові. Необхідно пам’ятати про те, що ці лінії повинні виступати за контури деталі на 1–3 мм.
Штрихпунктирною потовщеною лінією позначають поверхні, які підлягають покриттю або термообробці.
Розімкненою лінією позначають положення січних площин при позначенні розрізів та перерізів.
Штрихпунктирною лінією з двома точками позначають лінії згину на розгортках.
Таблиця 1.3 – Лінії креслення (ГОСТ 1.303–68)
|
Найменування |
Накреслення |
Товщина |
| Суцільна товста основна |
|
S = 0,5 – 1,4 мм |
| Суцільна тонка |
|
Від S/3 до S/1 |
| Суцільна хвиляста |
|
|
| Штрихова |
|
|
| Штрихпунктирна тонка |
|
|
| Штрихпунктирна потовщена |
|
Від S/1 до 1/3 S |
| Розімкнена |
|
Від S до 3/1 S |
| Суцільна тонка зі зломами |
|
Від S/3 до S/1 |
| Штрихпунктирна з двома точками |
|
Усі написи на кресленнях виконуються креслярським шрифтом, розміри якого та накреслення літер, цифр та знаків встановлює ГОСТ 1–304–81. Згідно з вимогами ГОСТ 1.304–81 шрифт буває без нахилу та з нахилом під кутом 750 до горизонту. На кресленнях усі написи рекомендовано виконувати з нахилом літер, цифр та знаків.
Літери, цифри та знаки повинні мати чітке накреслення, яке забезпечує швидке та однозначне їх сприймання. ГОСТ 1.304–81 регламентує написання літер російського, латинського та грецького алфавітів та арабських та римських цифр. У цьому ГОСТі також наведені приклади написання деяких знаків:
+ − (: ≈ =< >≤ ≥ ± (% ▻ ∅ □ №! [] ∫ ∞.
Шрифти розрізняють за розміром та типом.
Розмір шрифту визначається розміром великої літери та береться з ряду: 1,5; 3,5; 5; 7; 10; 14; 10. З цього ряду не рекомендується використовувати шрифт 1,5.
ГОСТ 1.304–81 встановлює типи шрифтів А та Б. Тип шрифту визначає товщину лінії накреслення шрифту. Цей параметр позначається літерою d.
Для типу А – d = 1/14h.
Для типу Б – d = 1/10h.
На рисунку 1.5 наведений український алфавіт (великі та малі літери).

Рисунок 1.5 – Український алфавіт
При побудові контурів деталей виникає необхідність виконувати різні геометричні побудови: ділити відрізок та коло на кілька рівних частин, виконувати спряження прямих ліній, кіл та прямої з колом, дугою заданого радіуса тощо.
Поділ відрізка на рівні частини
Для поділу відрізка на дві рівні частини необхідно послідовно виконати такі дії:
- з кінців відрізка циркулем провести дві дуги кіл, радіус яких повинен бути трохи більше половини даного відрізка, до взаємного перетину;
- з’єднати точки перетину проведених дуг;
- проведена лінія поділяє даний відрізок навпіл.
Поетапний поділ відрізка навпіл наведене на рисунку 1.6.

Рисунок 1.6 – Поділ відрізка навпіл
Щоб поділити відрізок на чотири рівні частини, необхідно виконати такі самі дії для поділу навпіл половини відрізка. На рисунку 1.7 відрізок АВ поділений на чотири рівні частини. Спочатку відрізок АВ поділений навпіл (АС=СВ), потім відрізки АС та СВ поділені ще раз навпіл.

Рисунок 1.7 – Поділ відрізка на чотири рівні частини
Для поділу відрізка на довільну кількість частин необхідно послідовно виконати дії, проілюстровані на рисунку 1.8:
- з будь-якого кінця відрізка (наприклад, з точки В) під гострим кутом провести промінь;
- від цієї ж точки відкласти довільну відстань стільки разів, на скільки необхідно поділити відрізок (наприклад, п’ять);
- з’єднати останню точку променя з другим кінцем відрізка;
- через точки поділу променя провести лінії, паралельні відрізку, який з’єднав кінцеву точку променя із заданим відрізком.

Рисунок 1.8 – Поділ відрізка на довільну кількість рівних частин
Поділ кута на рівні частини
Щоб поділити довільний кут навпіл або провести його бісектрису, необхідно послідовно виконати дії, проілюстровані на рисунку 1.9:
- з вершини кута провести дугу довільним радіусом до перетину зі сторонами кута (точки А та В);
- з точок перетину проведеної дуги зі сторонами кута провести дугу радіусом R, який більше половини відстані між точками А та В;
- з’єднати вершину кута та точку перетину дуг радіусами R – проведена лінія є бісектрисою кута, яка ділить кут навпіл.

Рисунок 1.9 – Ділення кута навпіл
Аналогічно можна поділити кут на чотири рівні частини.
Ділення прямого кута на три рівні частини виконують у такій послідовності:
- з вершини кута провести дугу довільним радіусом (R) до перетину зі сторонами кута;
- з визначених точок перетину провести дуги таким самим радіусом (R) до перетину з проведеною дугою;
- з’єднати вершину кута з визначеними точками.
На рисунку 1.10 наведене поетапне ділення прямого кута на три рівні частини.

Рисунок 1.10 – Ділення прямого кута на три частини
Ділення кола на рівні частини
На рисунку 1.11 наведений приклад ділення кола на чотири та вісім рівних частин. Точки 1, 3, 5, 7 ділення кола на чотири частини одержують в перетині осьових ліній із заданим колом. Для визначення положення точок 1, 4, 6, 8 застосовують спосіб ділення кута навпіл (рис. 1.9).

Рисунок 1.11 – Ділення кола на чотири та вісім рівних частин
Щоб поділити коло на три рівні частини (рис. 1.11 а), достатньо з точки А провести дугу кола, радіус якої дорівнює радіусу заданого кола до перетину з останнім у точках 1 та 3. Шукані точки1, 1, 3 ділять коло на три рівні частини.
Для ділення кола на шість рівних частин (рис. 1.11 б) необхідно з точок 1 та 4 провести дуги радіусом кола до перетину з останнім. Точки 1, 1, 3, 4, 5, 6 – ділять задане коло на шість рівних частин.
Щоб поділити коло на дванадцять частин (рис. 1.9 в), необхідно поділити його спочатку на шість частин, а потім з точок 4 та 10 провести такі самі дуги, щоб одержати точки 1, 6, 8 та 11. Точки 1, 1, 3, 4, 5, 6, 7, 8, 9, 10, 11, 11 – точки ділення кола на дванадцять рівних частин.

а) б) в)
Рисунок 1.11 – Ділення кола на три, шість та дванадцять частин
Приклад поетапного ділення кола на п’ять рівних частин наведений на рисунку 1.13.

Рисунок 1.13 – Ділення кола на п’ять рівних частин
Щоб поділити коло на п’ять рівних частин, необхідно послідовно виконати такі дії:
1) з точки А радіусом, який дорівнює радіусу даного кола, провести дугу, яка перетинає коло у точці n;
1) точка с визначається в перетині перпендикуляра, проведеного з точки n на горизонтальну осьову лінію. З точки с радіусом, який дорівнює відстані с1, провести дугу до перетину з горизонтальною осьовою лінією у точці m;
3) точка 1 визначається в перетині дуги кола радіусом 1m, проведеного з точки 1, із заданим колом;
4) для визначення точок, які поділять коло на п’ять рівних частин, необхідно циркулем послідовно зробити засічки на ньому радіусом, який дорівнює відстані 11.
Щоб поділити коло на сім рівних частин, необхідно послідовно виконати дії, проілюстровані на рисунку 1.14:
- з точки А радіусом, який дорівнює радіусу заданого кола, провести дугу, яка перетинає коло в точці n;
- з точки n опускають перпендикуляр на горизонтальну осьову лінію в точку с;
- довжину перпендикуляра nс (помічена двома рисками) відкладають від точки 1 по колу сім разів – одержують шукані точки 1 – 7.

Рисунок 1.14 – Ділення кола на сім рівних частин
Існує спосіб, який дозволяє поділити коло на будь-яку кількість рівних частин. На рисунку 1.15 наведене поетапне ділення кола на сім рівних частин цим універсальним способом.

Рисунок 1.15 – Ділення кола на сім рівних частин
Для ділення кола на n рівних частин послідовно виконують такі дії:
– діаметр заданого кола ділимо на n рівних частин (рис. 1.8);
– з точки С радіусом, який дорівнює діаметру заданого кола, робимо засічки на горизонтальній осі – точки А та В;
– з точок А та В проведені промені через парні (або непарні) ділення діаметра кола;
– проведені промені ділять коло на сім рівних частин. Якщо їх з’єднати, матимемо правильний семикутник, вписаний у коло заданого діаметра.
2 Побудова спряжень
Обриси багатьох технічних форм складаються з ліній, які плавно переходять одна в одну. Приклади таких деталей наведені на рисунку 1.16.

Рисунок 1.16 – Контури деталей
Плавний перехід від однієї прямої або кривої лінії до іншої називається спряженням. Основними видами спряження є: спряження двох прямих ліній, спряження двох кіл, спряження прямої та кола. Кожне з перелічуваних спряжень має свої закони побудови, але при побудові будь-якого спряження дугою заданого радіуса необхідно встановити центр спряження та початкову і кінцеву точки спряження.
Для побудови спряження двох взаємно перпендикулярних прямих дугою заданого радіуса (R) необхідно з точки перетину прямих провести дугу, радіус якої дорівнює радіусу спряження, до перетину з прямими (точки А та В). З точок А та В провести дуги радіусів R до їх взаємного перетину. Визначена точка О є центром спряження. З точки О провести дугу радіуса заданого спряження, обмеженого точками А та В. На рисунку 1.17 наведена поетапна побудова спряження двох взаємно перпендикулярних прямих.

Рисунок 1.17 – Спряження двох взаємно перпендикулярних прямих
На рисунку 1.18 наведений приклад поетапної побудови спряжень прямих, розміщених під гострим та тупим кутом. Центр спряження знаходиться в перетині допоміжних прямих, проведених паралельно заданим прямим на відстані радіуса спряження (R). Початкову та кінцеву точки спряження визначають в перетині перпендикулярів, які проведені з центра спряження на задані прямі.

Рисунок 1.18 – Спряження двох прямих, розміщених під гострим та тупим кутом
При виконанні спряження двох кіл можливі два випадки: зовнішнє спряження та внутрішнє. На рисунку 1.19 наведений приклад поетапної побудови зовнішнього спряження.

Рисунок 1.19 – Побудова зовнішнього спряження двох кіл
На першому етапі визначається центр спряження в перетині дуг кіл, проведених з центрів кожного кола. Радіус кожної дуги дорівнює сумі радіуса кола та радіусу спряження (відповідно R+R1 та R+R1).
На другому етапі визначаються початкова та кінцеві точки спряження в перетині прямих, які з’єднують центр спряження та центри кіл із останніми.
На останньому етапі з точки О проводиться дуга радіусом R між точками А та В.
Аналогічно будується внутрішнє спряження двох кіл дугою заданого радіуса. Поетапна побудова внутрішнього спряження наведена на рисунку 1.10. Центр спряження (точка О) знаходиться в перетині дуг радіусів R-R1 та R-R1, проведених з центрів заданих кіл.

Рисунок 1.10 – Побудова внутрішнього спряження двох кіл
При виконанні спряжень прямої лінії та кола можливі два варіанти – спряження може бути внутрішнім або зовнішнім.
На рисунку 1.11 наведене поетапне виконання внутрішнього спряження кола радіусом R1 та прямої l. R – радіус спряження.

Рисунок 1.11 – Внутрішнє спряження прямої та кола
Центр спряження (точка О) визначений в перетині прямої, яка паралельна заданій прямій l та віддалена від неї на відстані R, та кола радіусом R-R1, проведеного з центра заданого кола.
Для визначення початкової та кінцевої точок спряження необхідно з точки О провести перпендикуляр на l (точка А) та з’єднати центр спряження та центр заданого кола (точка В). Спряження проведено з точки О радіусом R від точки А до точки В.
На рисунку 1.11 наведений приклад поетапного виконання зовнішнього спряження прямої l та кола радіусом R1. Центр спряження (точка О) – визначається в перетині допоміжної прямої, яка паралельна заданій прямій l та віддалена від неї на відстані R, з колом радіуса R+R1, проведеним з центра заданого кола. Подальші побудови виконана у послідовності, описаній вище.

Рисунок 1.11 – Зовнішнє спряження прямої та кола
2.1 Лекальні криві
Лекальними називають криві, характерні точки яких з’єднуються за допомогою лекала.
До лекальних кривих відносять еліпс, параболу, гіперболу, синусоїду, спіраль Архімеда, евольвенту, циклоїдну криву тощо.
Еліпс – це плоска крива, для довільної точки якої сума відстаней до двох фіксованих точок (фокусів F1 та F1) є величиною сталою та дорівнює довжині великої його осі. Поетапна побудова еліпса наведена на рисунку 1.13.
Побудову еліпса можна виконати за шість етапів:
1 Відкласти значення великою та малої осей еліпса на відповідних осях. З перетину осей провести два концентричних кола, діаметри яких дорівнюють відповідно великій та малій осям еліпса.
2 Поділити кола на будь-яке число рівних або нерівних частин.
3 З точок поділу великого кола провести лінії, паралельні малій осі еліпса.
4 З точок поділу малого кола провести лінії, паралельні великій осі еліпса.
5 Визначити точки, які належать еліпсу: це точки, які обмежують велику та малу осі еліпса, та точки, знайдені у перетині допоміжних прямих (проведених відповідно до пунктів 3 та 4).
6 З’єднати точки, які належать еліпсу, за допомогою лекала. Для точності побудов поступово з’єднують по три точки.

Рисунок 1.13 – Поетапна побудова еліпса
Парабола – плоска крива, кожна точка якої рівновіддалена від директриси – прямої, перпендикулярної до осі симетрії параболи, та від фокуса – точки, яка належить осі симетрії параболи. Для побудови параболи існують кілька способів. На рисунку 1.14 наведена поетапна побудова параболи, яка здійснюється у такій послідовності:
1 За вихідними даними побудувати прямокутник CDEG.
1 Відстані DА та АE поділити на n рівних частин (у наведеному прикладі-6). З кожної точки ділення провести вертикальні лінії, паралельні осі параболи.
3 Сторони прямокутника CD та EG ділять на таку саму кількість рівних частин (шість частин). Вершину параболи (точку А) з’єднують з вертикальними точками ділення.
4 У перетині допоміжних прямих одержують точки, які належать параболі.
5 Шукані точки поступово з’єднують за допомогою лекала.

Рисунок 1.14 – Поетапна побудова параболи
Синусоїда – плоска крива, утворена траєкторією точки кінця радіуса-вектора, який рівномірно обертається навколо центра і одночасно рівномірно поступально переміщується вздовж осі х. На рисунку 1.15 наведене поетапне виконання синусоїди. Вихідними даними є діаметр кола та період синусоїди.
Діаметр кола та відрізок періоду синусоїди поділити на будь-яку кількість рівних частин. Точки поділу кола позначені цифрами 1 – 11, а точки поділу відрізка періоду синусоїди – цифрами 11 – 111. Точки синусоїди знаходять в перетині горизонтальних прямих, проведених з точок ділення кола, та вертикальних прямих, проведених через точки поділу відрізка періоду синусоїди. Шукані точки з’єднують плавною кривою за допомогою лекала.

Рисунок 1.15 – Поетапна побудова синусоїди
Спіраль Архімеда – плоска крива, утворена траєкторією точки, що рівномірно рухається вздовж радіуса-вектора, який, у свою чергу, рівномірно обертається навколо нерухомого центра.
Для побудови спіралі Архімеда (рисунок 1.16) за заданим її кроком (величина кроку дорівнює відрізку 0 11) необхідно з точки 0 провести коло, радіус якого дорівнює кроку. Поділити коло та крок на довільну кількість рівних частин: точки 11-111 – це точки ділення кола, а точки 1 – 11 – точки ділення кроку.
Точки спіралі лежать на перетині радіальних променів, що сполучають точки поділу кола та його центр, і дуг кіл, проведених через відповідні точки поділу кроку спіралі.

Рисунок 1.16 – Спіраль Архімеда
Евольвентою називають криву, що є траєкторією точки прямої лінії, що котиться без ковзання по нерухомому колу. На рисунку 1.17 наведений приклад побудови евольвенти. Щоб побудувати множину точок евольвенти, коло ділять на довільну кількість рівних частин (у наведеному прикладі-8). З кожної точки поділу проводять дотичну до кола, на якій відкладають відрізок, що дорівнює довжині дуги кола від початкової точки до заданої.

Рисунок 1.17 – Евольвента
Циклоїдами називають криві, які є траєкторією руху точки кола, що без ковзання котиться по прямій або кривій. Вихідними даними для побудови циклоїди є коло певного радіуса. На рисунку 1.18 наведений приклад побудови циклоїди.

Рисунок 1.18 – Циклоїда
На першому етапі на горизонтальній прямій, яка є дотичною до заданого кола, відкласти відстань, що дорівнює довжині кола. Коло та пряму поділити на довільну кількість рівних частин (наприклад, на 11 частин).
На другому етапі необхідно з точок поділу прямої провести перпендикуляри до перетину з продовженням горизонтальної осі кола (точки О1 – О11).
На наступному етапі необхідно з точок поділу кола провести горизонтальні прямі, на яких зробити засічки дугами заданого кола, проведеними з точок О1 – О11.
На останньому етапі шукані точки поступово з’єднують за допомогою лекала.
2.2 Нанесення розмірів
Розміри, що наносяться на кресленні, повинні бути підставою для визначення величини, форми та взаємного розміщення елементів деталі незалежно від масштабу зображення. Загальна кількість розмірів на кресленні повинна бути мінімальною, але достатньою для виготовлення та контролю даної деталі.
Розміри поділяють на лінійні та кутові. Лінійні розміри зазначають у міліметрах без позначення одиниць вимірювання. Кутові розміри зазначають у градусах, хвилинах, секундах з нанесенням одиниць вимірювання, наприклад 4о; 4111511.
ГОСТ 1.307–68 встановлює основні правила нанесення розмірів на кресленнях.
Розміри на креслення виносять за допомогою виносних та розмірних ліній та розмірного числа. При нанесенні лінійних розмірів розмірні лінії проводять паралельно відрізку, розмір якого зазначається, а виносні – перпендикулярно до нього. При нанесенні кутових розмірів виносні лінії проводять радіально, а розмірні – по дузі. На рисунку 1.19 наведені приклади нанесення лінійних та кутових розмірів.

Рисунок 1.19 – Приклади нанесення лінійних та кутових розмірів
Розмірну лінію з двох сторін обмежують стрілками, розміри яких наведені на рисунку 1.30.

Рисунок 1.30 – Розміри стрілки
Виносна лінія виходить за розмірну на 1–5 мм. Відстань розмірної лінії від паралельної їй лінії контуру та між паралельними розмірними лініями повинна бути у межах 6–10 мм. Як правило, перша розмірна лінія проводиться на відстані 10 мм від лінії контуру, а всі інші – на відстані 6–8 мм. На рисунку 1.31 наведений приклад нанесення розмірів та положення виносних і розмірних ліній відносно контурів деталі.

Рисунок 1.31 – Положення виносних та розмірних ліній
Розмірне число проставляють приблизно посередині над розмірною лінією креслярським шрифтом висотою 3.5 – 5 мм. Якщо на кресленні нанесено кілька паралельних розмірних ліній, їх записують у шаховому порядку (рис. 1.31).
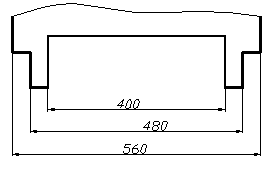
Рисунок 1.31 – Приклад нанесення розмірів
Якщо при нанесенні розмірів стрілка перетинає контурну або виносну лінію, їх переривають. На рисунку 1.33 наведені приклади таких варіантів нанесення розмірів.

Рисунок 1.33 – Варіанти нанесення розмірів
У місцях нанесення розмірного числа лінії осьові та лінії штрихування переривають (рис. 1.34).

Рисунок 1.34 – Варіанти нанесення розмірів
Якщо на розмірній лінії недостатньо місця для нанесення стрілок, то їх наносять зовні, та розмірне число записують так, як показано на рисунку 1.35.

Рисунок 1.35 – Варіанти нанесення розмірів
Якщо для написання розмірного числа недостатньо місця над розмірною лінією, то розміри наносять так, як показано на рисунку 1.36.
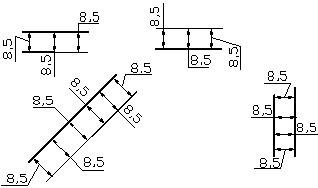
Рисунок 1.36 – Варіанти нанесення розмірів
Розміри фасок, які виконуються під кутом 45о, наносять так, як показано на рисунку 1.37 а, розміри фасок під іншими кутами позначають за загальними правилами – лінійним та кутовим розмірами (рис. 1.37 б).

а) б)
Рисунок 1.37 – Нанесення розмірів фаски
При нанесенні розмірів користуються допоміжними знаками, розміри яких встановлені ГОСТ 1.307–68.
При нанесенні розміру радіуса перед розмірним числом записують літеру R, розмір якої дорівнює висоті розмірного числа, наприклад, R5.
Різні варіанти нанесення розмірів зовнішнього та внутрішнього спряжень наведені на рисунку 1.38.

Рисунок 1.38 – Радіуси внутрішнього та зовнішнього спряжень
При великій величині радіуса центр допускається наближати до дуги, а розмірну лінію виконувати зі зломом під кутом 90о (рис. 1.39).
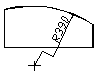
Рисунок 1.39 – Позначення розміру великого радіуса
При нанесенні розмірів діаметрів до його числового значення додається знак діаметра Æ, наприклад Æ10. Співвідношення розмірів елементів знака наведені на рисунку 1.40.
![]()
Рисунок 1.40 – Співвідношення елементів знака діаметра
На рисунку 1.41 наведені різні варіанти нанесення розмірів діаметрів.

Рисунок 1.41 – Варіанти нанесення розміру діаметра
За необхідності розмір діаметра може бути зазначений з обриванням розмірної лінії. Це можливо у випадках, коли зображення виконують із суміщенням половини вигляду та половини розрізу деталі, а також коли через один центр проведено кілька розмірних ліній діаметрів кіл (рисунок 1.41). Обривання розмірної лінії роблять трохи далі від осьової лінії деталі.

Рисунок 1.41 – Варіанти нанесення розмірів діаметра
Розмір сфери задають її радіусом або діаметром. Перед позначенням радіуса або діаметра сфери додається знак сфери – коло, діаметр якого дорівнює висоті розмірного числа. На рисунку 1.43 наведений приклад позначення розміру сфери.

Рисунок 1.43 – Позначення розміру сфери
Перед розмірним числом поверхні, яка має в перерізі форму квадрата, ставлять знак квадрата □, розмір якого дорівнює висоті маленької літери. Приклад позначення розміру квадрата наведений на рисунку 1.44.

Рисунок 1.44 – Позначення розміру квадрата
Перед розмірним числом, яке визначає конусність, ставлять знак конусності, гострий кут якого спрямований у бік вершини конуса. Розмір конусності можна ставити над осьовою лінією або на поличці лінії-виноски. Різні варіанти нанесення на кресленні конусності наведені на рисунку 1.45.

Рисунок 1.45 – Позначення конусності
Розміри кількох однакових елементів деталі або виробу наносять один раз з позначенням кількості елементів на поличці лінії-виноски.
Кількість однакових фасок зазначають під розмірною лінією так, як наведено на рисунку 1.46.

Рисунок 1.46 – Позначення однакових фасок
Кількість однакових отворів зазначають над розмірною лінією перед позначеним діаметром отвору або під поличкою (рисунок 1.47). Перевагу віддають першому варіанту.

Рисунок 1.47 – Позначення на кресленні однакових отворів
Розміри двох симетрично розміщених елементів деталі наносять на кресленні один раз без зазначення кількості елементів (рис. 1.48).

Рисунок 1.48 – Позначення на кресленні однакових елементів
Розміри за довжиною вала наносять ланцюгом або координатним способом (від загальної бази) На рисунку 1.49 зверху наведений приклад нанесення розмірів за довжиною вала ланцюгом, а знизу – координатним способом. На практиці, як правило, використовують комбінований спосіб нанесення розмірів по довжині вала (рис. 1.50).

Рисунок 1.49 – Варіанти нанесення розмірів по довжині вала

Рисунок 1.50 – Приклад нанесення розмірів по довжині вала
| Нарисна геометрія | |
|
Нарисна геометрія Вступ Засновником "Нарисної геометрії" є видатний французький геометр кінця VXIII - початку XIX століття Гаспар Монж. У своєму ... Щоб отримати ортогональні проекції точки на дві взаємно перпендикулярні площини проекцій, необхідно з точки простору (точка А) послідовно провести перпендикуляри до перетину їх з ... Координатні осі ізометрії розміщені під кутом 1200, поетапна побудова яких наведена на рисунку 1.58. |
Раздел: Рефераты по математике Тип: курсовая работа |
| Геометричні місця точок на площині та їх застосування | |
|
КУРСОВА РОБОТА на тему: "Геометричні місця точок на площині та їх застосування" Вступ Актуальність дослідження. Поняття геометричного місця точок у ... Отже, всі точки М шуканого геометричного місця лежать на колі Аполлонія, коли R=r, і на прямій, якщо R=r. 2) пару прямих р1 і р2 паралельних ВС і віддалених від ВС на даній відстані r; 3) пару сегментів, які містять кут ; 4) точку О як одну із точок перетину згаданих геометричних місць ... |
Раздел: Рефераты по математике Тип: курсовая работа |
| Комп"ютерна технологія графогеометричного моделювання. Взаємозвязок 2D ... | |
|
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ КУРСОВА РОБОТА З ДИСЦИПЛІНИ "ІНЖЕНЕРНА І КОМП'ЮТЕРНА ГРАФІКА" НА ТЕМУ "КОМП"ЮТЕРНА ТЕХНОЛОГІЯ ГРАФОГЕОМЕТРИЧНОГО ... Діалогове вікно Advanced Setup (Детальная подготовка) крім цього дозволяє визначити одиниці вимірювання кута (Angle (Углы)), задати початок (Angle Measure (Отсчет угла)) і напрям ... 2. Полярні координати: r < A, де r - радіус; A - кут від попередньої точки. |
Раздел: Рефераты по информатике, программированию Тип: курсовая работа |
| Математичний більярд | |
|
Вступ Обрана мною тема курсової роботи - математичні більярди - є дуже цікавою і актуальною. В умовах розвитку комп"ютерних технологій, створень ... Звідсіля |F1C1| + |F2C1| = |F1C2| + |F2C2|, де С1 і С2 - точки перетину АА1 з В1F2 i AA2 з B2F1.Значить, С1 і С2 лежать на одному еліпсі з фокусами F1 і F2, для якого відрізки АА1 ... LINE1(n, r0, r) - пряма, що проходить через точку r0 перпендикулярно вектору n (r - радіус-вектор довільної точки прямої); LINE2(q, r0, r) - пряма, що проходить через точку r0 ... |
Раздел: Рефераты по математике Тип: курсовая работа |
| ... математичних понять в процесі викладання математики в основній школі | |
|
ЗМІСТ Вступ Розділ 1. Теоретичні основи формування математичних понять 1.1. Поняття, як логіко-гносеологічна категорія 1.2. Об"єкт, поняття. Схожість ... Наприклад: "точки А і С лежать на прямій а", або "точки А і С належать прямій а"; "прямі а і b перетинаються в точці С", або "точка С є точкою перетину прямих а і b". Інший приклад, взаємно перпендикулярні прямі означають як прямі, що утворюють прямий кут. |
Раздел: Рефераты по математике Тип: дипломная работа |
-
Портал с рефератами
Тип: курсовая работа
| Математичний більярд | |
|
Вступ Обрана мною тема курсової роботи - математичні більярди - є дуже цікавою і актуальною. В умовах розвитку комп"ютерних технологій, створень ... Звідсіля |F1C1| + |F2C1| = |F1C2| + |F2C2|, де С1 і С2 - точки перетину АА1 з В1F2 i AA2 з B2F1.Значить, С1 і С2 лежать на одному еліпсі з фокусами F1 і F2, для якого відрізки АА1 ... LINE1(n, r0, r) - пряма, що проходить через точку r0 перпендикулярно вектору n (r - радіус-вектор довільної точки прямої); LINE2(q, r0, r) - пряма, що проходить через точку r0 ... |
Раздел: Рефераты по математике Тип: курсовая работа |
| ... математичних понять в процесі викладання математики в основній школі | |
|
ЗМІСТ Вступ Розділ 1. Теоретичні основи формування математичних понять 1.1. Поняття, як логіко-гносеологічна категорія 1.2. Об"єкт, поняття. Схожість ... Наприклад: "точки А і С лежать на прямій а", або "точки А і С належать прямій а"; "прямі а і b перетинаються в точці С", або "точка С є точкою перетину прямих а і b". Інший приклад, взаємно перпендикулярні прямі означають як прямі, що утворюють прямий кут. |
Раздел: Рефераты по математике Тип: дипломная работа |