Реферат: Классический метод математического описания и исследования многосвязных систем
Раздел: Рефераты по математике
Тип: реферат
КЛАССИЧЕСКИЙ МЕТОД
МАТЕМАТИЧЕСКОГО ОПИСАНИЯ И ИССЛЕДОВАНИЯ МНОГОСВЯЗНЫХ СИСТЕМ
1.1. ОСНОВНЫЕ ПОНЯТИЯ И РАСЧЕТНЫЕ ФОРМУЛЫ
Математическая модель линейной непрерывной многосвязной системы в физических переменных "вход-выход" при детерминированных воздействиях может быть представлена векторным дифференциальным уравнением в символическом виде [*]:
![]() ,
(1.1.1)
,
(1.1.1)
где ![]() – вектор размерности n
выходных координат системы;
– вектор размерности n
выходных координат системы; ![]() – вектор размерности m
управляющих воздействий;
– вектор размерности m
управляющих воздействий; ![]() – вектор размерности m1
возмущающих воздействий;
– вектор размерности m1
возмущающих воздействий; ![]() ,
, ![]() ,
, ![]() - полиномные матрицы размерностей
- полиномные матрицы размерностей
![]() ,
, ![]() ,
, ![]() соответственно,
элементы которых являются полиномами от р с постоянными коэффициентами
(например
соответственно,
элементы которых являются полиномами от р с постоянными коэффициентами
(например ![]() ,
,
![]() -
линейная комбинация относительно выходной координаты yj и ее производных);
-
линейная комбинация относительно выходной координаты yj и ее производных); ![]() -
символическое обозначение производной; t – время. При этом предполагается
существование соответствующих производных от y(t), u(t), r(t) по t и kL>kG,
kL>kN, где через kL, kG, kN обозначены порядки старших производных полиномов
от р в соответствующих матрицах L(p), G(p) и N(p).
-
символическое обозначение производной; t – время. При этом предполагается
существование соответствующих производных от y(t), u(t), r(t) по t и kL>kG,
kL>kN, где через kL, kG, kN обозначены порядки старших производных полиномов
от р в соответствующих матрицах L(p), G(p) и N(p).
Уравнение движения САУ составляется на основе ее структуры и математического описания, входящих в систему элементов, и имеет вид уравнения (1.1.1), где u(t)=z(t) и z(t) - вектор задающих воздействий на систему.
Уравнение движения САУ (1.1.1), записанное относительно у(t), называется уравнением автоматического управления (УАУ)
![]() ,
(1.1.2)
,
(1.1.2)
где ![]() ,
, ![]() - матричные
передаточные функции по задающему z(t) и возмущающему r(t) каналам соответственно.
- матричные
передаточные функции по задающему z(t) и возмущающему r(t) каналам соответственно.
Для определения собственных движений системы (1.1.1), то есть когда u(t)=0 (или z(t)=0) и r(t)=0, и ее порядка необходимо записать характеристический определитель
![]() , (1.1.3)
, (1.1.3)
и найти корни λj характеристического уравнения
![]() . (1.1.4)
. (1.1.4)
Система будет устойчивой,
если вещественная часть всех корней характеристического уравнения (нули функции
![]() ) будет
неположительной.
) будет
неположительной.
Общее решение неоднородной системы линейных дифференциальных уравнений может быть представлено в виде суммы общего решения yo(t) однородной системы и частного решения уч(t) исходной неоднородной системы
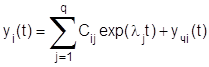 , (i=1,…,n), (1.1.5)
, (i=1,…,n), (1.1.5)
где: Cij - коэффициенты, определяемые начальными условиями дифференциальных уравнений; q - степень характеристического уравнения.
1.2. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1.1.1
Построить сигнальный граф математической модели динамического режима САУ, записанной в переменных "вход–выход" в символической форме векторно-дифференциальным уравнением вида:
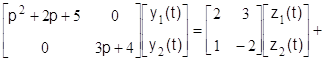
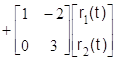 ,
, ![]() ,
, 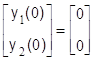 (1.2.1)
(1.2.1)
и определить характер свободного движения процесса по каналу “возмущающее воздействие r2 – выходная переменная y1“.
Решение
Сигнальный граф рассматриваемой САУ, в соответствии с уравнением (1.2.1) представлен на рис. 1.1.
Независимость выходных переменных yi в САУ определяется ее физическими свойствами и математически выражается в виде диагональности матрицы процесса L(p). На рис.1.1 независимость выходных переменных между собой отображается не связанностью вершин у1 и у2 сигнального графа, то есть независимостью уравнений между собой. Это позволяет решать уравнения независимо (отдельно) друг от друга.
![]()
y1



![]()
![]()
![]()
![]()
![]()
![]() z1 r1
z1 r1
![]()
![]()
![]()
![]()
![]()
![]()
![]() z2 r2
z2 r2
y2
Рис. 1.1. Сигнальный граф системы уравнений (1.2.1)
Для определения переходного процесса по каналу “возмущающее воздействие r2 – выходная переменная y1“ запишем его уравнение динамики
![]() , (1.2.2)
, (1.2.2)
которое представляет собой неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Решение данного уравнения дается формулой (1.1.5) при j=2.
Для определения корней λ1,2 запишем характеристическое уравнение соответствующего однородного дифференциального уравнения
![]() , (1.2.3)
, (1.2.3)
и решая его, получим ![]() ,
, ![]() . т. е. переходный процесс по рассматриваемому каналу является
колебательным асимптотически сходящимся.
. т. е. переходный процесс по рассматриваемому каналу является
колебательным асимптотически сходящимся.
Задача 1.1.2
Математические модели динамических режимов управляемой и управляющей подсистем в переменных "вход–выход" в символической форме описываются векторно-дифференциальными уравнениями вида:
а) управляемая подсистема
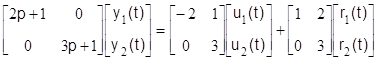 ,
,
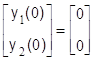 , (1.2.12)
, (1.2.12)
б) управляющая подсистема
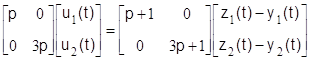 ,
(1.2.13)
,
(1.2.13)
при нулевых начальных условиях, где yi(t), ui(t), ri(t), zi(t) – выходные, управляющие, возмущающие переменные и задающие воздействия соответственно.
Задание
1. Составить структурную схему многомерной САУ на основе принципа управления по отклонению и сформировать в ней отрицательные обратные связи.
2. Получить уравнение динамики многомерной САУ и ее характеристическое уравнение.
Решение
1.Структурная схема двумерной САУ с информационными каналами в подсистемах представлена на рис. 1.2. Настоящая схема синтезируется на основе принципа управления по отклонению и уравнений (1.2.12), (1,2.13).
При формировании отрицательных обратных связей в системе необходимо учитывать, что количество элементов обратного действия в контуре управления должно быть нечетным.
1.1. Контур управления выходным параметром у1(t).
Управляемая подсистема по
каналу “![]() ”
– элемент обратного действия. Рассогласование
”
– элемент обратного действия. Рассогласование ![]() вводится в управляющее устройство
в виде
вводится в управляющее устройство
в виде ![]()
![]() , то есть
сумматор (элемент сравнения) является элементом обратного действия.
Следовательно, канал управляющей подсистемы в рассматриваемом контуре должен
содержать элемент обратного действия, поэтому элемент (р+1) матрицы должен быть
со знаком минус [-(p+1)].
, то есть
сумматор (элемент сравнения) является элементом обратного действия.
Следовательно, канал управляющей подсистемы в рассматриваемом контуре должен
содержать элемент обратного действия, поэтому элемент (р+1) матрицы должен быть
со знаком минус [-(p+1)].


![]()
![]()
![]()
![]()
![]()
![]() r1
r1
![]() r2
r2
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() z1
z1 ![]() u21
u11 y11
u21
u11 y11
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() z2
z2 ![]() u22
u12 y12
u22
u12 y12
 |
|||
![]() y22
y22
![]()
![]()
![]() y21
y21
![]()
![]()
![]() Рис. 1.2. Структурная схема двумерной
САУ
Рис. 1.2. Структурная схема двумерной
САУ
1.2. Контур управления выходным параметром у2(t).
Управляемая подсистема по
каналу “![]() ”
– элемент прямого действия. Рассогласование
”
– элемент прямого действия. Рассогласование ![]() вводится в управляющее устройство
в виде
вводится в управляющее устройство
в виде ![]()
![]() , то есть
сумматор (элемент сравнения) является элементом обратного действия.
Следовательно, канал управляющей подсистемы в рассматриваемом контуре должен
содержать элемент прямого действия.
, то есть
сумматор (элемент сравнения) является элементом обратного действия.
Следовательно, канал управляющей подсистемы в рассматриваемом контуре должен
содержать элемент прямого действия.
2. Составление уравнения динамики многомерной САУ и определение ее характеристического уравнения.
Заданные уравнения (1.2.12), (1.2.13) в общем виде можно записать как
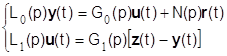 . (1.2.14)
. (1.2.14)
Исключив из системы уравнений (1.2.14) промежуточную переменную u, получим
![]() (1.2.15)
(1.2.15)
Перенося в левую часть
уравнения многочлен от y(t) и оставляя в правой части многочлены от независимых
переменных z(t), r(t) и учитывая, что ![]() , получим уравнение динамики
, получим уравнение динамики
![]()
![]() (1.2.16)
(1.2.16)
Характеристическое уравнение
![]() . (1.2.17)
. (1.2.17)
Задача 1.1.3
Математические модели динамических режимов управляемой и управляющей подсистем в переменных "вход–выход" описываются дифференциальными уравнениями вида:
а) управляемая подсистема
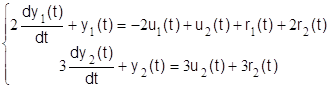 , (1.2.24)
, (1.2.24)
при нулевых начальных условиях;
б) управляющая подсистема
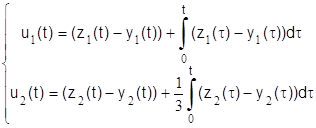 , (1.2.25)
, (1.2.25)
где yi(t), ui(t), ri(t), zi(t) – выходные, управляющие, возмущающие переменные и задающие воздействия соответственно.
Задание
1. Записать данные уравнения в символической форме и представить в векторно-дифференциальном виде;
Решение
Для записи данных
уравнений в символическом виде необходимо обозначение производной заменить на
символ р, то есть положить ![]() , а интеграл – на
, а интеграл – на ![]() . После замены получим
. После замены получим
а) управляемая подсистема
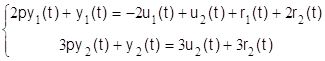 , (1.2.26)
, (1.2.26)
б) управляющая подсистема
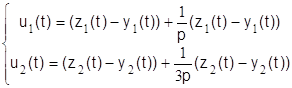 . (1.2.27)
. (1.2.27)
Вводя векторы y(t)=[y1(t), y2(t)]T, u(t)=[u1(t), u2(t)]T, r(t)=[r1(t), r2(t)]T и учитывая, что
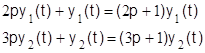 , (1.2.28)
, (1.2.28)
получим следующие уравнения:
а) управляемая подсистема
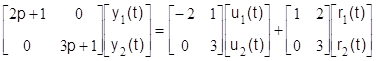 ,
,
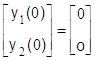 . (1.2.29)
. (1.2.29)
б) управляющая подсистема
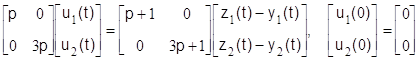 , (1.2.30)
, (1.2.30)
которые соответствуют уравнениям (1.2.12), (1.2.13) задачи 2.