Курсовая работа: Клеточные пространства

Содержание

Введение

1. Основные определения

1.1Терминологические замечания

1.2 Комментарии к определению клеточного пространства

2. Клеточные разбиения классических пространств

2.1 Сферы и шары

2.2 Проективные пространства

2.3 Многообразия Грассмана

2.4 Многообразия флагов

2.5 Классические поверхности

3. Гомотопические свойства клеточных пространств

3.1 Теорема Борсука о продолжении гомотопий

3.2 Следствия из теоремы Борсука

3.3 Теорема о клеточной аппроксимации

3.4 Доказательство леммы о свободной точке

3.5 Первые применения теоремы о клеточной аппроксимации

Заключение

Список использованных источников

Введение

В системе высшего образования весьма значительную роль играет гомотопическая топология, которая почти никогда не рассматривает совершенно произвольных топологических пространств. Обычно она изучает пространства с той или иной дополнительной структурой, причем со времен основоположника топологии Анри Пуанкаре рассматривают структуры двух типов. Первый тип - структуры аналитического происхождения: дифференциальная, риманова, симплектическая и т.д. Структуры второго, более важного для нас типа - комбинаторные структуры. Они заключаются в том, что пространство расчленено на более или менее стандартные, и изучение пространства сводится к изучению взаимного расположения этих частей.

Одна из важнейших из комбинаторных структур - клеточная структура. В гомологии она является эффективным вычислительным средством.

Данная работа посвящена изучению клеточной структуры, приведению некоторых теорем, свидетельствующие о полезности понятия клеточного пространства для гомотопической топологии., а так же подтверждающие необходимость изучения рассмотренной темы и всей топологии в целом, как основы для систематизации знаний по многим разделам высшей математики.

1. Основные определения

Клеточное пространство - это хаусдорфово топологическое пространство К, представленное в виде объединения  попарно непересекающихся множеств  ("клеток") таким образом, что для каждой клетки  существует отображение q-мерного шара  в К (характеристическое отображение, отвечающее клетке ), сужение которого на внутренность Int шара  представляет собой гомеоморфизм Int≈. При этом предполагаются выполненными следующие аксиомы.

(С) Граница = − клетки содержится в объединении конечного числа клеток  с r < q.

(W) Множество F К замкнуто тогда и только тогда, когда для любой клетки замкнуто пересечение F.

(Иногда характеристические отображения считаются фиксированными, т.е. рассматриваются как элемент структуры. Разумеется, такая модификация определения будет явно оговариваться)

1.1Терминологические замечания

1. Термин "клеточное пространство" не является абсолютно общепринятым: говорят также "клеточное разбиение" или "клеточный комплекс" или "CW-комплекс". Выражение "клеточное разбиение" мы будем употреблять как синоним выражения "разбиение пространства на клетки"; термин же "комплекс" будет у нас употребляться исключительно в алгебраическом значении.

2. Обозначения аксиом (С) и (W) являются стандартными; они происходят от английских слов "closure finite" и "weak topology".

Клеточное подпространство клеточного пространства K - это замкнутое его подмножество, составленное и целых клеток; клеточные подпространства являются самостоятельными клеточными пространствами. Важнейшие клеточные подпространства клеточного пространства - его остовы: n-й остов есть объединение всех клеток размерности  n (по определению, размерность клетки равна q). Стандартные обозначения для n-го остова пространства или X. Кстати, некоторые говорят "n-мерный остов", но это неправильно: размерность клеточного пространства определяется как верхняя грань размерностей его клеток, и, очевидно, размерность n-го остова меньше или равна n. Клеточное пространство называется конечным (счетным), если оно состоит из конечного (счетного) числа клеток.

Заметим, что для конечных клеточных пространств аксиомы (С) и (W) проверять не нужно: они выполняются автоматически.

1.2 Комментарии к определению клеточного пространства

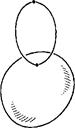
1. Замыкание клетки может не быть клеточным пространством. Пример: разбиение букета на клетки , и () - делает его клеточным пространством, но если а не есть отмеченная точка окружности , то замыкание последней клетки не является подпространством (см. рис.1).

Рис.1

2. Из (W) не следует (С). Разбиение диска D² на внутренность Int D² и отдельные точки граничной окружности удовлетворяет аксиоме (W) (потому что всегда F Int D ² = F), но не удовлетворяет аксиоме (С).

3. Из (С) не следует (W). Возьмем бесконечное семейство │α=1,2,…копий отрезка I, отождествим нулевые концы и топологизируем получившееся множество при помощи метрики: расстояние между точками , равно, если , и равно , если. Разбиение построенного пространства на множества и оставшиеся точки не удовлетворяет, из условий, входящих в определение клеточного пространства, только аксиоме (W): точки составляют последовательность, сходящуюся к 0, и, значит, незамкнутое множество, но пересечение этой последовательности с замыканием любой клетки замкнуто.

Кстати, если, как это только что было, разбиение пространства на клетки удовлетворяет всем условиям из определения клеточного пространства, кроме аксиомы (W), то можно ослабить в этом пространстве топологию, определив новую топологию при помощи аксиомы (W). Эта процедура называется "клеточным ослаблением топологии".

2. Клеточные разбиения классических пространств

2.1 Сферы и шары

При конечном n имеется два канонических клеточных разбиения сферы . Первое состоит из двух клеток: точки  (любой, скажем, (1,0,... ..., 0)) и множества  (рис.2а). Характеристическое отображение , отвечающее второй клетке, - это обычное "сворачивание" сферы из шара; годится, например, отображение, действующее по формуле , где (рис.3).

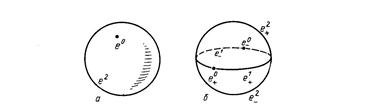
Рис.2

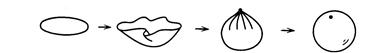
Рис.3

Другое каноническое клеточное разбиение сферы состоит из 2n +2 клеток : клетка  состоит из точек , у которых  и  (рис.2б). Заботиться о характеристических отображениях здесь не приходится: замыкание каждой клетки очевидным образом гомеоморфно шару соответствующей размерности.

Заметим, что оба описанные клеточные разбиения сферы  получаются из единственного возможного разбиения сферы  (двоеточия) посредством применения канонической конструкции клеточного разбиения надстройки: в первом случае нужно брать надстройку над сферой как над пространством с отмеченной точкой, а во втором случае - обыкновенную надстройку.

Существует, конечно, масса других клеточных разбиений сферы : ее можно разбить на 3ⁿ⁺¹ - 1 клеток как границу (n+1) - мерного куба, на  клеток - как границу (n+1) - мерного симплекса и т.п. .

Все описанные клеточные разбиения, кроме самого первого, годятся для сферы .

Клеточное разбиение шара  можно получить из любого клеточного разбиения сферы  путем присоединения одной клетки Int с характеристическим отображением id: . Наиболее экономное клеточное разбиение шара  состоит, таким образом, из трех клеток. Правда, ни одно из этих разбиений не годится для шара .

2.2 Проективные пространства

При отождествлении диаметрально противоположных точек сферы  клетки- клеточного разбиения склеиваются между собой и получается (n+1) - клеточное разбиение пространства R, по одной клетке  в каждой размерности q≤n. Это же разбиение можно описать так:

 R│.

Еще одно описание этого разбиения: имеется цепочка включений

 R R R R,

и мы полагаем e^q = R - R. Характеристическим отображением для e^q служит композиция канонической проекции D^q  R и включения RR. При n= наша конструкция доставляет клеточное разбиение пространства R, содержащее по одной клетке каждой размерности. Конструкция имеет также комплексный, кватернионный и кэлиев аналоги. Она дает: разбиение пространства С на клетки размерностей 0, 2, 4,..., 2n; разбиение пространства Hна клетки размерностей 0, 4, 8,..., 4n; разбиение пространства СаР² на клетки размерностей 0,8,16; клеточные разбиения пространств Си H, содержащие по одной клетке в каждой размерности, делящейся, соответственно, на 2 и 4. Например, пространство С разбивается на клетки

 С│

с характеристическими отображениями

C С.

2.3 Многообразия Грассмана

Описываемое ниже клеточное разбиение многообразий Грассмана очень важно для геометрии и топологии (особенно для теории характеристических классов). Составляющие его клетки называются клетками Шуберта, а само оно называется шубертовским.

Пусть  - произвольная конечная (возможно, пустая) невозрастающая последовательность целых положительных чисел, не превосходящих k, причем s ≤ n - k. Обозначим через e () подмножество пространства G (n,k), составленное из подпространств  пространства R, удовлетворяющих следующим условиям (мы полагаем =0):

R при m ≤ k - m;

codim  ( R) =о при ;

 R при m ≤ k + s + 1

(мы считаем, что R^a  R при a < b: ). Приведем другое, более простое описание множества e (). Напомним, что диаграмма Юнга набора  - это фигура, которая рисуется на клетчатой бумаге, как показано на рис.4а (столбцы имеют длины ).

Число клеток диаграммы Юнга равно . Можно считать, что клетки пространства G (n,k) отвечают диаграммам Юнга, вмещающимся в прямоугольник k (n - k) (рис.4а). Рассмотрим диаграмму Юнга набора и расположим ее, как показано на рис.4б. Толстая линия на этом рисунке представляет собой график некоторой неубывающей функции, и множество e () задается условием dim (R) =  (m). Ввиду наличия такого простого описания, множество e () обозначают иногда через е (), где  - обозначение для диаграммы Юнга набора (). Еще раз заметим, что размерность клетки е () равна числу клеток диаграммы.

Лемма. Множество e () гомеоморфно R.

Доказательство. Расчленим диаграмму Юнга набора (), как показано на рис.4в. Поставим в клетках вдоль косых линий единицы, в Заштрихованные клетки - произвольные числа и в остальные места - нули. Получится kn-матрица, строки которой составляют базис некоторого k-мерного подпространства пространства R. Легко понять, что это подпространство принадлежит e () и что всякое подпространство, принадлежащее e (), обладает единственным базисом указанного вида. Получаем параметризацию клетки e () наборами из  чисел (числа в заштрихованных клетках).

Рис.4

На самом деле верно больше: множества e () составляют клеточное разбиение пространства G (n, k). Для доказательства нужно построить характеристические отображения, т.е. продолжить построенные гомеоморфизмы IntR  e () до непрерывных отображений G (n, k), отображающих сферу  в объединение клеток меньших размерностей.

Замечательное свойство шубертовских клеток состоит в том, что при естественных вложениях G (n, k) в G (n+1, k) ив G (n+1, k+1) клетка e () гомеоморфно накладывается на клетку того же наименования. Следовательно, пространство G (,k) разбивается на клетки Шуберта, отвечающие диаграммам Юнга, содержащимся в горизонтальной полуполосе высоты k, а пространство G (,) разбивается на клетки, отвечающие всем без исключения диаграммам Юнга. Во всех случаях размерности клеток равны числам клеток диаграмм Юнга.

Комплексные и кватернионные аналоги шубертовских клеток очевидны; разумеется, размерности комплексных и кватернионных аналогов клеток Шуберта соответственно в 2 и 4 раза превосходят числа клеток соответствующих диаграмм Юнга.

2.4 Многообразия флагов

Многообразия флагов имеют естественное клеточное разбиение, обобщающее шубертовское разбиение многообразий Грассмана. Это разбиение и его клетки также называются шубертовскими. Опишем разбиение в вещественном случае (комплексный и кватернионный случаи отличаются только удвоением и учетверением размерностей клеток).

Шубертовские клетки многообразия флагов характеризуются наборами размерностей пересечений VR. Числа , однако, должны удовлетворять набору довольно неудобных условий, и мы предпочтем следующее, более рациональное описание клеток Шуберта.

Клетки пространства F (n; ) отвечают наборам  целых чисел, принимающих значения 1,…, s + 1, причем ровно  из этих чисел равны j (j=1,…, s+1; мы считаем, что k=0 и k=n). Клетка е [], отвечающая набору (), состоит из флагов VV, у которых

dim{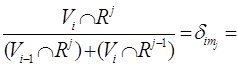

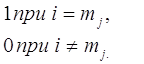
(мы считаем, что V=0 и V есть все пространство R) или, иначе,

dim (V R ) = card {р ≤ i│k_p ≤ j }.

Размерность клетки е [] равна числу пар (i, j), для которых i<j, >.

В частности, многообразие F (n; 1,…,n-1) полных флагов разбито на n! клеток, отвечающих обыкновенным перестановкам чисел 1,…, n, причем размерность клетки равна числу инверсий в перестановке.

Если многообразие флагов есть многообразие Грассмана G (n, k), то s = 1 и набор состоит из k единиц и n-k двоек. Построим по этому набору n-звенную ломаную на плоскости, начинающуюся в точке (0, k) и кончающуюся в точке (n-k, 0). Все звенья ломаной имеют длину 1, причем i-e звено направлено вниз, если  = 1, и вправо, если = 2. Эта ломаная ограничивает (вместе с координатными осями) некоторую диаграмму Юнга , и легко понять, что е [] = е ().

Заметим в заключение, что клетки е [] (и их комплексные и кватернионные аналоги) могут быть описаны чисто групповым образом: это - орбиты группы нижних треугольных nn-матриц с единицами на диагонали, естественным образом действующей в многообразии флагов. Именно, клетка е [] есть орбита флага, i-е пространство которого порождено координатными векторами, номера р которых удовлетворяют неравенству < i.

2.5 Классические поверхности

Клеточные разбиения поверхностей S² и RP² нами уже построены. Клеточные разбиения остальных поверхностей без края автоматически получаются при склеивании этих поверхностей из многоугольников: двумерная клетка получается из

внутренности многоугольника, одномерные клетки - из его (открытых) ребер, нульмерные клетки - из его вершин. Каноническое клеточное разбиение каждой классической поверхности имеет одну двумерную и одну нульмерную клетку. Кроме того, сфера с g ручками имеет 2g одномерных клеток (см. рис.5), проективная плоскость с g ручками имеет 2g +1одномерную клетку и бутылка Клейна с g ручками имеет 2g +2 одномерных клеток.

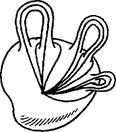
Рис.5

3. Гомотопические свойства клеточных пространств

3.1 Теорема Борсука о продолжении гомотопий

Определение. Пара (X, А) называется парой Борсука (или корасслоением), если для любого пространства Y и любого непрерывного отображения F: ХY всякая гомотопия f_t: АY, такая, что f = F│ _А, может быть продолжена до гомотопий F_t: ХY, у которой F₀ = F.

Теорема Борсука. Если X - клеточное пространство и А - его клеточное подпространство, то (X, А) - пара Борсука.

Доказательство. Нам даны отображения Ф: А I Y (гомотопия f_t) и F: X 0 Y, причем F │= Ф│. Продолжить гомотопию f_t до гомотопий F_t - это значит продолжить отображение F до отображения F’: XI  Y, такого, что F’ │= Ф. (Продолжение мы произведем индуктивно по размерности клеток пространства X, не входящих в А. Начальным шагом индукции служит продолжение отображения Ф на (AX) I:

F’ (x, t) ={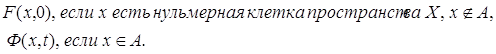

Допустим теперь, что отображение F' уже определено на (A  X)  I. Возьмем произвольную (n+ 1) - мерную клетку e Х - A. По предположению, F' задано на множестве () I, так как граница = клетки содержится в X по определению клеточного пространства. Пусть f: D X - характеристическое отображение, соответствующее клетке . Нам надо продолжить F' на внутренность "цилиндра" f (D) I с его "стенки" f (S) I и "дна" f (D)  0. Но из определения клеточного пространства ясно, что это все равно, что продолжить отображение  F’f: (SI)  (D 0) Y до непрерывного отображения ': D I Y.

Пусть : D I  (SI)  (D 0) - проектирование цилиндра D I из точки, лежащей вне цилиндра вблизи верхнего основания D I (см. Рис.6); это отображение тождественно на (SI)  (D 0). Отображение ' мы определяем как композицию

D I (SI)  (D 0) Y.

Эту процедуру можно проделать независимо для всех (n + 1) - мерных клеток пространства X, и мы получаем продолжение отображения F' на (A X)  I.

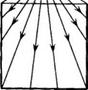
Рис.6

Так, остов за остовом, мы строим желаемое продолжение отображения Ф до отображения F: XI Y. Подчеркнем, что если пространство X бесконечномерно, то наше индуктивное построение будет состоять из бесконечного числа шагов; в этом случае непрерывность окончательного отображения будет следовать из аксиомы (W). Теорема доказана.

3.2 Следствия из теоремы Борсука

Следствие 1. Пусть X - клеточное пространство и А - его клеточное подпространство. Если А стягиваемо по себе в точку, то X/А ~ X.

Доказательство. Обозначим через  проектирование X  Х/А. Так как А стягиваемо, то существует гомотопия f_t: АА, такая, что отображение f₀: А А тождественно и f (A) есть точка. В силу теоремы Борсука, существует гомотопия F_t: ХХ, такая, что F₀ = id и F_t│_A =f_t. B частности F (A) =* (точка). Это означает, что можно рассматривать как отображение, заданное на Х/А, точнее, что F ⁼ q  p, где q: Х/А X - некоторое непрерывное отображение. По построению, F ~F₀, т.е. q  p ~ id.

Далее, F_t (А)  А (при любом t), т.е. р F_t (А) = *. Следовательно, р F_t = = q_t  р, где q_t: Х/А Х/А - некоторая гомотопия. При этом q = id иq = р q; следовательно, р q ~ id.

Следствие доказано.

Следствие 2. Если X - клеточное пространство и А - его клеточное подпространство, то Х/А ~ X СА, где СА - конус над А.

Доказательство. Х/А = (X  СА) /СА ~Х  СА; последнее вытекает из предыдущего следствия, примененного к клеточному пространству X  СА и его стягиваемому клеточному подпространству СА.

Замечание. Оба доказанных предложения можно рассматривать не как следствия из теоремы Борсука, а как самостоятельные теоремы, только предположения о клеточности X и А нужно тогда заменить в первом случае предположением, что (X, А) - пара Борсука, а во втором случае - предположением, что (X  СА, СА) - пара Борсука.

3.3 Теорема о клеточной аппроксимации

Теорема. Всякое непрерывное отображение одного клеточного пространства в другое гомотопно клеточному отображению.

Мы будем доказывать следующее, более сильное утверждение ("относительный вариант" нашей теоремы).

Теорема. Пусть f - непрерывное отображение клеточного пространства X в клеточное пространство Y, причем на клеточном подпространстве А пространства X отображение f клеточно. Тогда существует такое клеточное отображение g: XY, что g│_A =f│_A и, более того, f~g relA.

Поясним запись f~g relA (читается: f гомотопно g относительно А), которой мы будем пользоваться и дальше. Она применяется в ситуации, когда непрерывные отображения f, g: X Y совпадают на подпространстве А пространства X и означает, что существует гомотопия h: Х Y, соединяющая f с g и неподвижная на А, т.е. такая, что h_t (а) не зависит от t при а  А. Конечно, из f~ g relА следует, что f ~ g, но не наоборот. Пример: f,g: IS, f - "наворачивание" отрезка на окружность, g - отображение в точку; эти отображения гомотопны, но не гомотопны rel (01).

Доказательство теоремы. Предположим, что отображение f уже сделано клеточным не только на всех клетках из А, но и на всех клетках из X, имеющих размерность < р. Возьмем р-мерную клетку е^р X - А. Ее образ f (e^p) пересекается лишь с конечным числом клеток пространства Y (это следует из компактности f (^p)). Выберем среди этих клеток пространства Y клетку наибольшей размерности, скажем, , dim= q. Если q≤ р, то нам с клеткой е^р делать нечего. В случае же q >р нам потребуется следующая лемма.

Лемма о свободной точке. Пусть U - открытое подмножество пространства R^p и : U IntD^q - такое непрерывное отображение, что множество V =  (d^q) U, где d^q - некоторый замкнутый шарик в IntD, компактно. Если q> р, то существует непрерывное отображение : U Int D^q, совпадающее с  вне

V и такое, что его образ не покрывает всего шара d^q.

Доказательство этой леммы (и обсуждение ее геометрического значения) мы отложим до следующего пункта; ограничимся лишь важным замечанием, что отображение  автоматически будет гомотопным  относительно U - V: достаточно взять связывающую  с  "прямолинейную" гомотопию, при которой точка  (u) равномерно движется к  (u) точке по прямолинейному отрезку, соединяющему  (u) с  (u).

Завершим доказательство теоремы. Из леммы о свободной точке вытекает, что сужение f│  гомотопно rel (AX) отображению f’: A  X  е ^р Y, такому, что f’ (e^p) задевает те же клетки, что и f (e ^р), но заведомо f’ (e^p) не содержит всю клетку . В самом деле, пусть h: D^p Х, k: D^p Y - характеристические отображения, соответствующие клеткам е^р, . Положим U=h (f ()  е^р) и определим отображение : U Int D^q как композицию:

u x  y  =  (u)

U ef ()  Int D^q Обозначим через d^q (замкнутый) концентрический подшар шара D^q. Множество V=  (d^q) компактно (как замкнутое подмножество шара D^p). Пусть : U  IntD^q - отображение, доставляемое леммой о свободной точке. Отображение f' определим как совпадающее с f вне h (U) и как композицию

x  u    y = f’ (x)

h (U) U Int D^q Y

на h (U). Ясно, что отображение f’ непрерывно (оно совпадает с f на "буферном множестве" h (U - V)) и гомотопно f│rel (AX), и даже rel (AX (e-h (V)))) (это вытекает из гомотопности ~  rel (U - V)). Ясно также, что f' (e^p) не покрывает e^q.

Дальнейшее рассуждение совсем просто. Во-первых, неподвижную на A  Х гомотопию между f│ и f' мы можем распространить, по теореме Борсука, на все X, и это позволяет считать, что отображение f', обладающее всеми вышеперечисленными свойствами, определено на всем X. После этого мы берем точку у₀ , не принадлежащую f’ (е^р), и подвергаем f'│ "радиальной гомотопии": если точка xe^p не принадлежит f’ (),To f' (x) стоит на месте, а если f' (x) , то f’ (x) движется по отрезку, идущему из точки у₀ на границу клетки  (точнее говоря, по k-образу прямолинейного отрезка, начинающегося в точке k (у₀) проходящего через точку k (f’ (x))  k (у₀) и кончающегося на граничной сфере Sшара D^q). Эту гомотопию мы продолжаем до гомотопии отображения f'│ (неподвижной вне е^р) и - по теореме Борсука - до гомотопии всего отображения f’: ХY. Получающееся отображение f’’ гомотопно f ге1 (AХ) и обладает тем свойством, что f’’ (e^p) задевает q-мерных клеток на одну меньше, чем f (е ^р) (и, как и f (e^p), не задевает клеток размерности >q). Применив эту процедуру нужное число раз, мы прогомотопируем отображение f к отображению, клеточному на AХe^p, причем гомотопия будет неподвижной на AХ.

Теперь заметим, что "исправление" отображения f, которое мы проделали для клетки е^р, можно дословно так же проделать одновременно для всех р-мерных клеток из X - А. Тогда мы придем к отображению, клеточному на A Х^р и гомотопному f rel (AХ).

Неподвижную на А гомотопию, связывающую отображение f с клеточным отображением, мы получим, если проделаем последовательно построенные гомотопии при р = 0, 1,2,... Правда, число этих гомотопии может быть бесконечно, но это не беда: р-ю гомотопию мы производим на отрезке 1 - 2≤t≤ 1 - 2. Непрерывность всей гомотопии обеспечивается аксиомой (W): для каждой клетки е из X гомотопия будет неподвижной, начиная с некоторого t_e < 1. Теорема доказана.

3.4 Доказательство леммы о свободной точке

Для человека, не испорченного популярной математической литературой, сама формулировка леммы показалась бы нелепой: как же непрерывный образ пространства меньшей размерности может покрыть пространство большей размерности? Но кто же не знает, что это бывает: кривая Пеано, распропагандированная ничуть не меньше, чем, скажем, бутылка Клейна, осуществляет непрерывное (и даже взаимно однозначное) отображение отрезка на квадрат. Поэтому лемму приходится доказывать, и дело осложняется тем, что геометрическая интуиция помочь тут не может, она упорно твердит свое: такое вообще невозможно. С подобными трудностями сталкиваются всякий раз, когда "строгое" определение того или иного понятия (в данном случае --определение непрерывности) не вполне соответствует исходному интуитивному представлению: приходится вникать в устройство не реального объекта, а химеры. Но ничего не поделаешь - доказать лемму надо.

В основе второго доказательства леммы лежит понятие триангуляции. Напомним, что q-мерный евклидов симплекс есть подмножество пространства R, n ≤ q, являющееся выпуклой оболочкой q + 1 точек, не лежащих в одной (q - 1) - мерной плоскости. (Евклидовы симплексы размерностей 0, 1, 2, 3: точка, отрезок, треугольник, тетраэдр.) Эти q+ 1 точек называются вершинами симплекса. Подсимплексы, т.е. выпуклые оболочки различных подмножеств множества вершин, называются гранями нашего симплекса; это - симплексы размерности ≤q. Нульмерная грань - это вершина. Замечательное свойство симплекса заключается в том, что его линейное отображение в любое пространство R^m определяется своими значениями на вершинах, причем эти значения могут быть совершенно произвольны. Конечная триангуляция подмножества евклидова пространства - это такое его конечное покрытие евклидовыми симплексами, что любые два симплекса либо не пересекаются вовсе, либо пересекаются по целой грани. Удобно считать, что грани симплексов триангуляции также принадлежат к числу симплексов триангуляции.

Барицентрическое подразделение q-мерного симплекса состоит в том, что этот симплекс разбивается на (q + 1) ! более мелких q-мерных симплексов. Вершины новых симплексов - это центры тяжести граней старого симплекса (в том числе - его самого). Множество {х₀, х,..., x_q) этих центров является множеством вершин некоторого симплекса барицентрического подразделения, если соответствующие грани ₀, ,..., _q можно составить в цепочку последовательно вложенных друг в друга, см. рис.7. (По-другому барицентрическое подразделение q-мерного симплекса  можно описать так: сначала подвергаются барицентрическому подразделению все его (q - 1) - мерные грани, а потом над всеми построенными симплексами, лежащими на границе симплекса , строятся конусы с вершиной в центре этого симплекса; начать это индуктивное определение можно с q = 0: с нульмерным симплексом при барицентрическом подразделении ничего не происходит. Еще по-другому: симплекс  - его совокупность точек вида , где  - вершины, t≥ 0 и t = 1; симплексы барицентрического подразделения отвечают перестановкам (i₀, i,..., i_q) чисел 0, 1,..., q; симплекс, отвечающий этой перестановке, состоит из точек

t с .

Барицентрическое подразделение триангуляции - это триангуляция, составленная из симплексов барицентрических подразделений симплексов исходной триангуляции (рис.8).

Обратимся теперь к нашему отображению . Прежде всего мы построим в шарике d = d_q концентрические шарики d, d₂, d₃, d радиусов /5, 2/5, З/5,4/5, где -радиус шарика d. Далее, покроем V конечным числом р-мерных симплексов, содержащихся в U, и триангулируем объединение К этих симплексов (объединение конечного числа как угодно пересекающихся евклидовых симплексов в R^p обладает конечной триангуляцией). Применив к этой триангуляции достаточное число

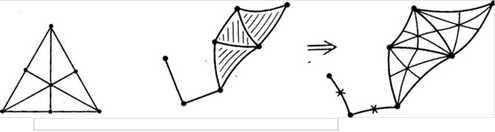
Рис.7                                                                            Рис.8

раз барицентрическое подразделение, мы можем добиться того, чтобы для любого симплекса  триангуляции выполнялось неравенство diam () < /5. Пусть K₁ - объединение симплексов построенной триангуляции нашего множества К,-образы которых пересекаются с d₄. Тогда d₄ < (U)  (K₁) d. Рассмотрим отображение ': К₁  d, совпадающее с  на вершинах триангуляции и линейное на каждом симплексе. Отображения │_K и ’ гомотопны - они соединяются прямолинейной гомотопией _t: K₁d, ₀=│_K, ₁ = ’. Теперь "сошьем" отображения  и ’ в отображение : UIntD^q:

 (u), если  (u) d_3, (u) = ’ (u), если  (u) d_{2,3-5 (u) (}u), если  (u) d₃-d₂.

Здесь  (u) - расстояние от точки  (u) до центра шара d. (См. рис.9)

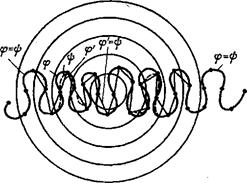
Рис.9

Отображение  непрерывно, совпадает с  на U - V и его образ пересекается с d₁ по конечному числу кусков р-мерных плоскостей, т.е. всего шара d₁ (а значит, и всего шара d) не покрывает.

Лемма доказана.

3.5 Первые применения теоремы о клеточной аппроксимации

Теорема. Если X - клеточное пространство с единственной вершиной (= нульмерной клеткой), не имеющее других клеток размерности <q, a Y - клеточное пространство размерности <q, то всякое отображение YX гомотопно отображению, переводящему все Y в точку. Такое же утверждение справедливо в категории пространств с отмеченными точками (в клеточной ситуации удобно считать, что отмеченными точками являются нульмерные клетки).

Это прямо следует из теоремы о клеточной аппроксимации: если f: Y  X - клеточное отображение, то так как q-й остов пространства Y есть все Y, а q-й остов пространства X есть точка, то f (Y) - точка.

В частности, если m < q, то  (S^m, S^q) = _b (S^m, S^q) = 0 (т.е. состоит из одного элемента).

Оп ределение. Пространство X называется n-связным, если при q ≤ n множество  (S^q, X) состоит из одного элемента (т.е. если любые два отображения S^q  X с q ≤ n гомотопны).

Теорема. Всякое п-связное клеточное пространство гомотопически эквивалентно клеточному пространству с единственной вершиной и без клеток размерностей 1, 2,..., n.

Доказательство. Выберем в нашем пространстве X вершину е₀ и соединим с ней остальные вершины путями. Это можно сделать, так как пространство n-связно и, в частности, линейно связно. (Пути могут пересекаться) Используя теорему о клеточной аппроксимации, мы можем добиться того, чтобы эти пути лежали в одномерном остове пространства X. Пусть s_i - путь, соединяющий вершину е₀ с вершиной е_i. Приклеим при каждом i к X двумерный диск по отображению нижней полуокружности в X при помощи пути s_i (рис.10).

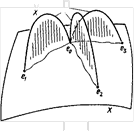
Рис.10

Получим новое клеточное пространство X, которое будет содержать X и, кроме того, клетки е, е (верхние полуокружности и внутренности приклеенных писков). То, что границы клеток е лежат в одномерном остове, вытекает из того, что этим свойством обладают пути s_i. Ясно, что X есть деформационный ретракт в : каждый Фприклеенный диск можно смять на нижнюю полуокружность.

Обозначим через Y объединение замыканий клеток е_i¹. Очевидно, Y стягиваемо; следовательно,  /Y ~ ~ X. Но у /Y всего одна вершина.

Дальнейшее рассуждение совершенно аналогично. Предположим, что X ~ X’, причем X' имеет единственную вершину и не имеет клеток размерностей 1,2,..., k - 1, где k≤n. В этом случае замыкание каждой k-мерной клетки представ ляет собой k-мерную сферу. Ввиду n-связности X (и, следовательно, X^’) включение этой сферы в X' продолжается до непрерывного отображения (k + 1) - мерного шара, образ которого, ввиду теоремы о клеточной аппроксимации, можно считать лежащим в (k + 1) - м остове пространства X'. По этому отображению (которое мы считаем отображением нижней полусферы (k + 1) - мерной сферы) мы приклеиваем к X'. шар D^k+2, и подобным образом мы поступаем для каждой k-мерной клетки пространства X’. Полученное клеточное пространство ’ гомотопически эквивалентно X’ и содержит стягиваемое подпространство Y - объединение замыканий всех вновь приклеенных (k + 1) - мерных клеток (верхних полусфер приклеенных шаров), содержащее все k-мерные клетки. Имеем: ’ /Y ~ ’ ~ X’ ~ X, ’ /Y имеет единственную вершину и не имеет клеток размерностей 1,2,...,k.

Следствие. Если клеточное пространство X п-связно, а клеточное пространство Y n-мерно, то множество  (Y, X) состоит из одного элемента. Это же верно для _b (Y, X), если X и Y имеют отмеченные точки, являющиеся вершинами.

Замечание. Использованная в доказательстве последней теоремы процедура уничтожения k-мерных клеток предполагает присоединение клеток размерности k + 2. В случае, если заданное n-связное пространство было (n + 1) - мерно, это могло привести к увеличению размерности. В действительности можно доказать, что всякое n-связное клеточное пространство размерности n + 1 гомотопически эквивалентно букету (n + 1) - мерных сфер.

Последняя теорема имеет относительный вариант, для формулировки которого необходимо понятие n-связной пары. Топологическая пара (X, А) называется n-связной, если всякое отображение (Dⁿ, S^n-1)  (X, А) гомотопно (как отображение пар) отображению, загоняющему все Dⁿ в А.

Заключение

В данной курсовой работе был собран и обобщен материал, касающийся вопросов, связанных с важнейшей комбинаторной структурой топологии - клеточной структурой.

Цель курсовой работы - изучение основных понятий клеточной структуры топологии, выяснение ее значимости - была достигнута.

Для достижения цели была проработана литература, рассмотрены определение клеточного пространства, клеточные разбиения классических пространств, а также некоторые теоремы о клеточных пространствах.

Результаты проделанной работы могут быть использованы студентами физико-математических факультетов при изучении разделов топологии, а также для анализа и систематизации курсов математического анализа, дифференциальных уравнений, дифференциальной геометрии и других дисциплин.

Список использованных источников

1.         Болтянский В.Г., Ефремович В.А. Наглядная топология. - М.: Наука, 1983. - 160 с.

2.         Борисович, Ю.Г. Введение в топологию: Учеб. пособие для вузов / Ю.Г. Борисович, Н.М. Близняков, Я.А. Израилевич, Т. Н Фоменко - М.: Высш. школа, 1980. - 295 с.

3.         Гарднер, М. Математические досуги / М. Гарднер − М.: Мир, 1972. − 496 с.

4.         Зейферт Г., Трельфалль В. Топология. - М. - Л.: ГОНТИ, 1938. - 400 с.

5.         Куратовский, К. Топология: В 2 т. / К. Куратовский − М.: Мир, 1966, т. I, − 594 с; 1969, т.П. − 624 с.

6.         Рохлин, В.В., Фукс Д.Б. Начальный курс топологии. Геометрические главы / В.В. Рохлин, Д.Б. Фукс − М.: Наука, 1977. − 488 с.

7.         Спеньер, Э. Алгебраическая топология / Э. Спеньер; перевод с англ. Б.М. Пранова; под ред.А.М. Виноградова - М.: Мир, 1971 - 680с.

8.         Стинрод, Н. Чинн У. Первые понятия топологии / Н. Стинрод, У. Чинн − М.: Мир, 1967. − 224 с.

9.         Фоменко, А.Т., Фукс, Д.Б. Курс гомотопической топологии: учеб. пособие для вузов. - М.: Наука. Гл. ред. Физ. - мат. Лит., 1989. - 528 с.