Контрольная работа: Оптимальные методы в совершенствовании планирования и управления производством
Содержание
1 Содержание ЭММ и методика их построения. Роль оптимальных методов в совершенствовании планирования и управления производством
2 Экономико-математические модели оптимальной загрузки производственных мощностей
3 Постановка и содержание ЭММ отраслевого прогнозирования и регулирования
Список использованных источников
1. Содержание ЭММ и методика их построения. Роль оптимальных методов в совершенствовании планирования и управления производством
Содержанием любой экономико-математической модели является выраженная в формально-математических соотношениях экономическая сущность условий задачи и поставленной цели. В модели экономическая величина представляется математическим соотношением, но не всегда математическое соотношение является экономическим. Описание экономических условий математическими соотношениями - результат того, что модель устанавливает связи и зависимости между экономическими параметрами или величинами. Наиболее полное - законченное определение экономико-математической модели дал академик В. С. Немчинов: "Экономико-математическая модель представляет собой концентрированное выражение общих взаимосвязей и закономерностей экономического явления в математической форме".
По содержанию различают экономико-математические и экономико-статистические модели. Различие между ними состоит в характере функциональных зависимостей, связывающих их величины. Так, экономико-статистические модели связаны с показателями, сгруппированными различными способами. Статистические модели устанавливают зависимость между показателями и определяющими их факторами в виде линейной и нелинейной функции. Экономико-математические модели включают в себя систему ограничений, целевую функцию.
Система ограничений состоит из отдельных математических уравнений или неравенств, называемых балансовыми уравнениями или неравенствами.
Целевая функция связывает между собой различные величины модели. Как правило, в качестве цели выбирается экономический показатель (прибыль, рентабельность, себестоимость, валовая продукция и т. д.). Поэтому целевую функцию иногда называют экономической, критериальной. Целевая функция - функция многих переменных величин и может иметь свободный член.
Критерий
оптимальности - экономический показатель,
выражающийся при помощи целевой функции через другие экономические показатели.
Одному и тому же критерию оптимальности могут соответствовать несколько разных,
но эквивалентных целевых функций. Модели с одной и той же системой ограничений
могут иметь различные критерии, оптимальности и различные целевые функции.
Смешивать понятия критерия оптимальности и целевой функции нельзя. Критерий
оптимальности есть понятие модельное, экономическое. Критерии оптимальности
могут быть натуральные и стоимостные. Одни из критериев - максимизируемые,
другие - минимизируемые. Из минимизируемых критериев является критерий
совокупных затрат труда всех видов, предложенный А. Г. Аганбегяном и А. Г.
Гранбергом. Он выражается целевой функцией ![]() ,
где
,
где ![]() - вектор совокупных затрат
труда, элементы которого означают объемы затрат труда в каждом js-м технологическом способе при его
единичной интенсивности.
- вектор совокупных затрат
труда, элементы которого означают объемы затрат труда в каждом js-м технологическом способе при его
единичной интенсивности.
Из максимизируемых критериев можно выделить такие, как: число наборов конечных продуктов, валовая, конечная, чистая и условно чистая продукция, прибыль, рентабельность и др.
Решением экономико-математической модели, или допустимым планом называется набор значений неизвестных, который удовлетворяет ее системе ограничений. Модель имеет множество решений, или множество допустимых планов, и среди них нужно найти единственное, удовлетворяющее системе ограничений и целевой функции. Допустимый план, удовлетворяющий целевой функции, называется оптимальным. Среди допустимых планов, удовлетворяющих целевой функции, как правило, имеется единственный план, для которого целевая функция и критерий оптимальности имеют максимальное или минимальное значение. Если модель задачи имеет множество оптимальных планов, то для каждого из них значение целевой функции одинаково.
Если экономико-математическая модель задачи линейна, то оптимальный план достигается в крайней точке области изменения переменных величин системы ограничений. В случае нелинейной модели оптимальных планов и оптимальных значений целевой функции может быть несколько. Поэтому необходимо определять экстремальные планы и экстремальные значения целевой функции. План, для которого целевая функция модели имеет экстремальное значение, называют экстремальным планом, или экстремальным решением.
Целевая функция, зависящая от переменных величин в заданной области изменения последних, всегда достигает наибольшего и наименьшего значения или вовсе его не имеет. Экстремальные значения целевой функции достигаются внутри, а оптимальные значения достигаются также и на границе области изменения переменных величин. Поэтому экстремальные значения целевой функции могут совпадать с оптимальными, однако это не значит, что все оптимальные значения целевой функции есть экстремальные. Для нелинейных моделей иногда существуют экстремальные значения целевой функции, а для линейных моделей экстремальных планов и экстремальных значений целевой функции быть не может.
Таким образом, для принятия оптимального решения любой экономической задачи необходимо построить ее экономико-математическую модель, по структуре включающую в себе систему ограничений, целевую функцию, критерий оптимальности и решение.
Методика построения экономико-математической модели состоит том, чтобы экономическую сущность задачи представить математически, используя различные символы, переменные и постоянные величины, индексы и другие обозначения.
Все
условия задачи необходимо записать в виде уравнений или неравенств, поэтому, в
первую очередь необходимо определить систему переменных величин, которые могут
для конкретной задачи обозначить искомый объем производства продукции на
предприятии, количество перевозимого груза поставщиками конкретным потребителям
и т. д. Как правило, для обозначения переменных величин используются буквы: x, y, z, а также их модификации.
Например, модификация переменной x: ![]() ,
, ![]() ,
, ![]() ,
, ![]() и т. д. Аналогичные
модификации могут быть и для других переменных, используемых в модели. Переменные
x1, x2, … , хn могут обозначать объемы производства продукции соответственно
первого, второго и так далее п-го вида. Для индексации, как правило,
используются латинские буквы: i, j, s, l. Количество переменных может обозначаться
буквами n, k, m. По каждой переменной для конкретной
задачи дается словесное пояснение.
и т. д. Аналогичные
модификации могут быть и для других переменных, используемых в модели. Переменные
x1, x2, … , хn могут обозначать объемы производства продукции соответственно
первого, второго и так далее п-го вида. Для индексации, как правило,
используются латинские буквы: i, j, s, l. Количество переменных может обозначаться
буквами n, k, m. По каждой переменной для конкретной
задачи дается словесное пояснение.
Целевую функцию - цель задачи - чаще всего обозначают буквами f, F, Z. Постоянные величины обычно обозначают буквами: a, b, c, d и т. д.
Ограничения модели должны отражать все условия, формирующие оптимальный план. Однако практически учесть все условия задачи для достижения цели невозможно, достаточно учесть основные условия. Естественно, полученная модель будет упрощенной по сравнению с реальной, которая отражала бы все условия поставленной задачи.
Итак, в упрощенном виде экономико-математическая модель представляет собой:
1) систему ограничений - равенства, неравенства вида больше или равно (≥), меньше или равно (≤);
2) условия неотрицательности
переменных, исходя из экономической или физической сущности переменных (![]() );
);
3) целевую функцию.
Математически общую модель задачи можно представить в виде:
Найти значения n переменных x1, x2, … , хn, которые удовлетворяют системе ограничений:
f(x1, x2, … , хn) {≤,=,≥} bi (![]() ); (1.1)
); (1.1)
и максимизируют или минимизируют целевую функцию
Z=f(x1, x2, … , хn,) (1.2)
Если на переменные налагается условие неотрицательности, тогда в модель задачи вводится условие:
![]() (1.3)
(1.3)
Иногда на переменные налагается условие целочисленности, тогда его можно записать в виде:
![]() , или 1, или 2, или 3 и т. д. (1.4)
, или 1, или 2, или 3 и т. д. (1.4)
Если ограничения (1.1) и целевая функция (1.2) линейны относительно переменных, то модель называют линейной. В случае, если хотя бы одна из функций fi и Z нелинейна, то модель называют нелинейной.
Одной из важнейших предпосылок создания единой системы оптимального управления народным хозяйством является разработка теории оптимального функционирования экономики. Ее отличительная особенность состоит в последовательном применении принципа оптимальности, к решению всего сложного комплекса проблем анализа, планирования и управления народным хозяйством. На основе понимания экономики как сложной системы, реализующей объективный критерий оптимальности своего развития, теория оптимального функционирования экономики исследует в качественном и количественном аспектах проблемы соизмерения затрат и результатов производства, рационального распределения и использования ограниченных трудовых и материальных ресурсов общества, оптимальных темпов и пропорций развития народного хозяйства, наилучшего сочетания интересов производственных единиц и всего общества и др.
Существенное значение имеет разработка экономико-математического обеспечения системы оптимального функционирования экономики. На основе теории оптимального функционирования экономики и современных математических методов необходимо создать комплекс экономико-математических моделей, дающих количественную характеристику всех основных закономерностей, связей и процессов в народном хозяйстве. Модели должны опираться на весь накопленный опыт планирования и управления хозяйством. В них должна быть заложена возможность получения наиболее эффективных, оптимальных планов на всех уровнях - от отдельного предприятия до народного хозяйства в целом. Вместе с тем комплекс моделей должен обеспечить возможность максимального использования экономических рычагов рационального ведения хозяйства: цен, прибыли, хозрасчета, материального стимулирования. Только в этом случае оптимально составленный план будет сочетаться с оптимальными условиями и стимулами его выполнения. В математическом отношении для создания комплекса моделей потребуются все уже существующие методы: математического программирования, дифференциального и интегрального исчисления, матричных балансовых построений, теории вероятностей и математической статистики и другие, более сложные и пока недостаточно разработанные методы экономико-математического моделирования. К экономико-математическому обеспечению системы оптимального функционирования экономики можно отнести и собственно математическое ее обеспечение, т. е. комплекс алгоритмов и программ, обеспечивающих решения задач оптимального планирования и управления на электронных вычислительные машинах.
Для создания информационного обеспечения системы оптимального функционирования экономики необходимо коренное совершенствование системы экономической информации. Существующая экономическая информация не унифицирована, вследствие чего показатели плановой, учетной, финансовой, снабженческо-сбытовой информации не только отличны друг от друга, но зачастую вообще несопоставимы. Направления и объемы "пересылаемой информации четко не определены, пересылаются излишние, почти не используемые получателями сведения в ущерб действительно необходимым данным. Потоки хозяйственной информации не уменьшаются, а растут.
В условиях применения экономико-математических методов и электронной вычислительной техники необходимо создание единой системы экономической информации, охватывающей все существующие ее виды. Направления, объемы и сроки передачи информации должны быть точно установлены, при этом количество различных пересылаемых и хранимых сведений должно быть минимальным при максимальном их содержании и использовании. Эта задача выходит за рамки простого упорядочения информации и является в настоящее время большой научной проблемой. Опыт применения экономико-математических методов показал, что существующее нормативное хозяйство, данные учета и статистики зачастую недостаточны или непригодны для постановки и решения задач оптимального планирования. Это выдвигает проблему совершенствования нормирования, учета и статистики как предпосылку создания системы оптимального функционирования экономики.
Наконец, система оптимального управления народным хозяйством нуждается в мощном техническом обеспечении в виде государственной сети вычислительных центров, сопряженной с; автоматизированной сетью связи страны. Как и система экономической информации, сеть вычислительных центров должна строиться по междуведомственному принципу. Вычислительные центры (от низовых до головного) должны быть оснащены достаточно мощными вычислительными машинами, приспособленными к экономическим расчетам, и связаны между собой с помощью современных средств электрической связи. Единая государственная сеть вычислительных центров будет осуществлять хранение, обработку и передачу всей экономической информации в стране, и все расчеты по оптимальному планированию и управлению народным хозяйством.
Народнохозяйственную эффективность создания системы оптимального функционирования экономики трудно переоценить. Однако эта работа потребует еще немалого времени и усилий и преодоления серьезных трудностей научного и практического порядка.
2 Экономико-математические модели оптимальной загрузки производственных мощностей
Модели оптимальной загрузки производственного оборудования относятся к линейно программным моделям, которые могут быть успешно использованы для текущего планирования. На основе этих моделей отыскивается оптимальный вариант формирования или распределения производственной программы по группам оборудования, позволяющий улучшить технико-экономические показатели работы завода, цеха, участка, повысить коэффициент загрузки оборудования, выявить излишние производственные фонды и т. п.
Пусть j - индекс (номер) вида производимой продукции или осуществляемых деталеопераций. При продуктовой классификации это могут быть виды деталей, узлов, а также готовых изделий. В общем случае – j=1, ... ,n , где n - общее число производимых видов продукции.
Коэффициенты затрат времени обработки детали j-го вида на оборудовании i-ой группы (для удобства можно рассчитывать затраты на обработку 10, 100 шт. и т. д.) рассчитываются па базе технологической нормы времени обработки детали рассматриваемого вида на определенной группе станков с учетом планового коэффициента выполнения прогрессивных норм по следующей формуле:
![]() ,
,
где fij - технологическая норма времени обработки детали вида j на оборудовании i-ой группы (в станко-час);
![]() - плановый коэффициент выполнения норм на i-ой группе оборудования;
- плановый коэффициент выполнения норм на i-ой группе оборудования;
![]() - коэффициент приведения норм к прогрессивному
уровню.
- коэффициент приведения норм к прогрессивному
уровню.
Норму времени fij получают непосредственно из операционных и технологических карт процесса обработки деталей. При этом она рассматривается как сумма штучного времени обработки деталей на данной группе станков (определяемого типом станка, режимом его работы, наличием оснастки и приспособлений, а также количеством деталей, обрабатываемых на одном приспособлении одновременно).
В рассматриваемой линейной модели загрузки оборудования такие параметры, как размер партии деталей, очередность их обработки на различных станках, календарные графики загрузки оборудования и т. п., не оптимизируются. Они принимаются заданными для каждого из производственных способов.
Обозначим
полезный фонд времени (в станко-час) по i-й группе оборудования через Аi. Ограничения по полезному фонду времени работы каждой
группы оборудования зададим исходя из действительного (располагаемого) фонда
времени в станко- или машино-час. В результате располагаемый фонд времени по
данной технологической группе определяется, во-первых, количеством единиц
оборудования по этой группе qi и, во-вторых, годовым (квартальным, месячным и т. д.) полезным фондом
времени по каждой единице оборудования ![]() (станко-час),
где l=1, ... , qi – индекс единицы оборудования данной
группы. Расчет осуществляем по формуле:
(станко-час),
где l=1, ... , qi – индекс единицы оборудования данной
группы. Расчет осуществляем по формуле:
![]()
Следует отметить, что по отдельным производственным участкам, где используется недорогое и недефицитное оборудование или выпускается крупногабаритная продукция (например, в формовочных отделениях литейных цехов), лимитирующими факторами могут быть производственные площади.
В принятых обозначениях имеем следующую систему ограничений модели оптимальной загрузки мощностей:
● потребность в фонде времени работы оборудования не должна превышать действительного фонда времени
![]() (1)
(1)
здесь yi - величина резерва времени по i-й группе оборудования, этот «резерв» образуется, если имеет место недогрузка оборудования группы i;
● ограничения неотрицательности переменных
![]() (2)
(2)
Во внутризаводском планировании наиболее часто формулируется задача на оптимум по критерию максимума загрузки мощностей:
![]() (3)
(3)
При использовании этого критерия подбирается такая номенклатура выпуска продукции, которая обеспечивает максимальный коэффициент загрузки оборудования. Таким образом, цель, состоящая в максимизации выпуска продукции (повышения рентабельности), достигается косвенно, через максимизацию загрузки оборудования, что соответствует, в известной мере, внутрицеховому критерию наилучшего использования мощностей. Такой подход с практической точки зрения привлекает главным образом своей простотой.
Для приведения в определенное соответствие подбираемой номенклатуры выпуска продукции установленному плану может быть целесообразно формулировать в модели (1) - (3) двусторонние ограничения по производственной программе:
![]()
где E2 – множество видов продукции, по которым такие ограничения существенны.
Развитие модели (1) - (3) состоит в рассмотрении ряда производственно-технологических способов выпуска продукции, а также в использовании ценностных критериев (максимума прибыли и минимума себестоимости) и критерия максимума выпуска продукции в заданном ассортименте.
При
применении моделей загрузки взаимозаменяемых групп оборудования определяется
оптимальный вариант использования фонда времени работы станков, которые могут
выполнять одинаковые деталеоперации, но с различной производительностью.
Например, определяется максимальная загрузка парка универсальных токарных
станков, оснащенных различными инструментами и приспособлениями, полуавтоматических
и автоматических станков и т. п. Типовой моделью, с помощью которой решаются
такие задачи, является модель распределительной или ![]() -задачи
линейного программирования.
-задачи
линейного программирования.
Модель
загрузки взаимозаменяемых групп оборудования отличается специфической
структурой формулировки производственных способов: по каждому способу деталь
определенного j-го вида производится лишь на одной i-й группе оборудования, затраты
станочного времени при этом составляют ![]() (станко-час/шт.).
При этом в систему ограничений включаются способы производства деталей каждого
вида на каждой группе оборудования.
(станко-час/шт.).
При этом в систему ограничений включаются способы производства деталей каждого
вида на каждой группе оборудования.
Интенсивность применения технологии (i, j) характеризует производство деталей j-го вида на i-м оборудовании хij (шт.), а эффективность ее использования выражается показателем прибыли pij (руб./шт.) или затрат cij (руб./шт.). Если же j-я деталь не может быть произведена на i-й группе оборудования, то технология (i, j) получает «запрет» - искусственно заниженный показатель прибыли или завышенный показатель себестоимости, что гарантирует неиспользование этого способа в оптимальном плане.
Система ограничений модели оптимизации загрузки взаимозаменяемых групп оборудования содержит:
● баланс между необходимым и располагаемым фондами времени по каждой группе оборудования
![]() (4)
(4)
● ограничения неотрицательности
![]() (5)
(5)
● ограничения на выпуск продукции всех видов
![]() (6)
(6)
Функция цели – максимум суммарной прибыли от производства всей продукции:
![]() (7)
(7)
При заданной программе Вj план загрузки взаимозаменяемых групп оборудования, определяемый по критерию максимума прибыли, совпадает с решением задачи на минимум себестоимости. В этом случае система ограничений модели не изменяется, а целевая функция принимает вид:
![]() ,
,
где сij - себестоимость изготовления детали вида i на j-ой группе оборудования.
При
решении задачи на минимум затрат станочного времени в ограничениях и критерии
оптимальности будут использоваться одни и те же показатели ![]() (станко-час/шт.), т. е.
целевая функция примет вид:
(станко-час/шт.), т. е.
целевая функция примет вид:
![]()
В модели оптимальной загрузки взаимозаменяемых групп оборудования может быть также использован ассортиментный критерий оптимальности.
Практически
важным является случай, когда распределительная задача сводится к транспортной
задаче линейного программирования. Транспортная задача есть частный случай ![]() - задачи при всех
- задачи при всех ![]() . Ее специфика заключается
в том, что ресурсы и потребности выражаются в
одних и тех же единицах, в то время как в распределительной задаче
единицы измерения ресурсов (фонд времени работы оборудования в станко-час) и
продукции (программа в шт.) различаются. Для сведения задачи максимизации
загрузки оборудования к транспортной задаче необходимо выразить ресурсы и
продукцию в стандартных станко-часах, что удастся сделать, если
производительность каждой группы станков, включенных в рассмотрение, но всем
деталям в одинаковое число раз отличается от производительности одного из станков,
принятого за стандартный.
. Ее специфика заключается
в том, что ресурсы и потребности выражаются в
одних и тех же единицах, в то время как в распределительной задаче
единицы измерения ресурсов (фонд времени работы оборудования в станко-час) и
продукции (программа в шт.) различаются. Для сведения задачи максимизации
загрузки оборудования к транспортной задаче необходимо выразить ресурсы и
продукцию в стандартных станко-часах, что удастся сделать, если
производительность каждой группы станков, включенных в рассмотрение, но всем
деталям в одинаковое число раз отличается от производительности одного из станков,
принятого за стандартный.
3. Постановка и содержание ЭММ отраслевого прогнозирования и регулирования
Модели отраслевого прогнозирования и регулирования весьма трудоемки, характеризуются многофакторностью, динамичностью исходных данных и, зачастую, целочисленностью решений и нелинейностью целевой функции. Все это усложняет постановку конкретных экономико-математических задач и их моделирование. При разработке и решении задач оптимального отраслевого и регионального регулирования (ООРР) учитывают взаимозаменяемость ресурсов и потребностей, действующее и новое производство, различные способы производства продукции, варианты использования капитальных вложений на реконструкцию и новое строительство и т. д. На стадии прогнозирования стратегии развития отрасли эти параметры могут быть достаточно точно учтены, что обеспечивает определение наиболее точных вариантов развития отрасли.
Объектами ООРР являются предприятия, месторождения сырьевых ресурсов, трубопроводы и т. д. Как действующие, так и проектируемые по альтернативным вариантам их развития. Они увязываются в моделях с конкретными потребителями и совокупной потребностью в каждом виде конечной продукции.
Важным условием решения задач ООРР является соблюдение определенной последовательности перехода от одного отраслевого блока к другому. Блоки располагаются в таком порядке, чтобы решение предшествующей отраслевой задачи предоставляло максимум информации для решения последующей задачи. Очевидно, что полностью обратные связи исключить нельзя, но их можно свести к минимуму. По мнению академика А. Г. Аганбегяна систему отраслевых блоков можно представить в следующей последовательности:
- агрокомплекс;
- химический комплекс;
- машиностроительный комплекс;
- комплекс черной металлургии;
- комплекс цветной металлургии;
- топливно-энергетический комплекс;
- лесопромышленный комплекс;
- транспорт.
Задачи ООРР дадут экономический эффект в том случае, если при их построении будут использоваться достоверные исходные данные. Прогноз развития отрасли требует формирования большого круга показателей и оценки их численных значений. Состав исходной информации определяется постановкой задачи и выбранной экономико-математической моделью. Например, при решении задачи перспектив развития и размещения предприятий отрасли в рамках статической модели потребуются следующие данные:
1) необходимый объем производства продукции данной отрасли;
2) альтернативные способы функционирования действующих предприятий;
3) возможные пункты размещения предполагаемых новых предприятий и способы их функционирования;
4) ожидаемая потребность в продукции в разрезе районов потребления;
5) затраты на транспортировку продукции от предприятий до районов потребления.
При использовании динамической модели исходные данные готовятся в разрезе временных интервалов, обусловленных постановкой задачи.
Задачи ООРР занимают промежуточное положение между моделями оптимального планирования микроэкономики (управление работой предприятиями, фирмами, потребителями) и макроэкономическими моделями прогнозирования и регулирования размеров и структуры общественного продукта, создаваемого всеми отраслями народного хозяйства. Оптимальный прогноз развития отрасли даже в условиях развивающихся рыночных отношений не является планом, директивой, поскольку государство не гарантирует производителям сбыт производимой ими продукции. В то же время реализация решенных на ЭВМ задач ООРР позволяет лучше решать многие социально-экономические проблемы, укреплять социально-политическую стабильность, сохранять окружающую среду, гармонизировать отношения с внешним миром. Хотя такие решения не всегда совпадают с сиюминутными экономическими интересами отдельных фирм, предприятий.
Выход в этой ситуации не в отказе от разработки и решения задач ООРР, гарантирующих социально-экономическую эффективность обществу, а в усилении роли государственного регулирования экономикой. Рыночная экономика в "чистом" виде не предполагает вмешательства государства в процесс производства и обмена. Это - саморегулирующийся механизм. Однако в странах СНГ она только начинает формироваться. Что касается развитых стран дальнего зарубежья, то там государство применяет десятки рычагов для регулирования рыночных отношений. Для этой цели используются субсидии, налоговые льготы, государственные заказы и т. д. Рыночный механизм не позволяет своевременно сосредотачивать ресурсы для приоритетного развития отдельных отраслей и ускоренной структурной перестройки промышленности. Это под силу только государству. Незаменимым помощником в этом деле может быть экономико-математическое моделирование ООРР.
Рассмотрим общую целочисленную модель отраслевого регулирования. Эта модель используется в отраслях, где транспортный фактор несущественно влияет на размещение и специализацию производства, например, для решения задач размещения предприятий отдельных видов производства машиностроения, приборостроения, ремонтных предприятий, легкой промышленности и т. д.
Обозначим:
i - номер
предприятия (![]() );
);
j - номер вида продукции (![]() );
);
k - номер варианта развития i-го предприятия (![]() );
);
s - номер вида ресурсов (![]() );
);
Bj - необходимый объем продукции j-го вида;
Ds - общий объем ограниченных ресурсов s-го вида;
![]() - объем производства j-ой
продукции на i-м предприятии при k-ом
варианте его развития;
- объем производства j-ой
продукции на i-м предприятии при k-ом
варианте его развития;
![]() - величина расхода s-x ресурсов на i-м предприятии при k-ом варианте его развития;
- величина расхода s-x ресурсов на i-м предприятии при k-ом варианте его развития;
![]() - искомые величины (булевы переменные), означающие интенсивности способов
(вариантов) производства;
- искомые величины (булевы переменные), означающие интенсивности способов
(вариантов) производства;
![]() - значение оценок переменных в целевой функции модели (величина
капиталовложений на i-м предприятии при k-ом варианте его развития, приведенные затраты и т. д.).
- значение оценок переменных в целевой функции модели (величина
капиталовложений на i-м предприятии при k-ом варианте его развития, приведенные затраты и т. д.).
В
принятых обозначениях задача сводится к следующему: найти значения переменных ![]() , при которых
минимизируется величина целевой функции
, при которых
минимизируется величина целевой функции
![]() (1)
(1)
и выполняются условия
![]() (2)
(2)
- все предприятия отрасли должны произвести не меньше заданного объема по каждому виду продукции;
![]() (3)
(3)
- все предприятия отрасли могут использовать дефицитные ресурсы в рамках имеющихся возможностей или лимитов;
![]() (4)
(4)
- условие целочисленности переменных величин. Переменная величина равна единице, если данный вариант развития i-го предприятия используется в оптимальном плане, или равен нулю, если он не используется.
В
задачах оптимального отраслевого регулирования существует большое множество
вариантов плана (векторов ![]() )
удовлетворяющих условиям (1) – (4). Во время решения задачи на ЭВМ из этого
множества выбирается такой вектор интенсивности
)
удовлетворяющих условиям (1) – (4). Во время решения задачи на ЭВМ из этого
множества выбирается такой вектор интенсивности ![]() ,
при котором минимизируется значение целевой функции (1). Эти значения
,
при котором минимизируется значение целевой функции (1). Эти значения ![]() будут оптимальным планом
при принятых условиях. Подстановка этого вектора в систему (1) – (4) позволит
определить конкретные показатели плана.
будут оптимальным планом
при принятых условиях. Подстановка этого вектора в систему (1) – (4) позволит
определить конкретные показатели плана.
При решении конкретных задач в систему (1) – (4) могут вводиться дополнительные ограничения и переменные величины. Например, ограничения на мощность отдельных предприятий или группы предприятий; ограничения и переменные, отражаемые возможность взаимозамещаемости отдельных ресурсов или продукции и т. д.
Рассмотрим данную модель на условном примере:
Пусть требуется произвести два вида продукции в объеме 20 и 10 ед. соответственно. Они могут производиться на двух предприятиях. Использование лимитированного ресурса ограничено 100 ед. По каждому предприятию разработаны два варианта их развития, отличающиеся объемом производства продукции, величиной расхода ресурсов и приведенными затратами на весь выпуск. Данные приведены в таблице 1.
Таблица 1
| Предприятия, i | Варианты развития предприятий, к |
Виды продукции и объемы их производства, |
Величина расхода ресурсов, |
Приведенные затраты, |
Интенсивность вариантов производства, |
|
| 1 (20) | 2 (10) | |||||
|
1 |
2 |
3 |
3 |
2 |
4 |
|
|
|
1 |
5 |
4 |
3 |
8 |
|
|
2 |
2 |
5 |
4 |
5 |
7 |
|
|
|
1 |
15 |
6 |
6 |
9 |
|
Развернутая запись задачи будет иметь вид:
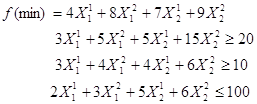
Результат решения данной задачи:
Х* = (0;1;0;1)
f(Х*) = 17(8+9)
Прогнозируемый объем производства двух видов продукции необходимо разместить на двух предприятиях отрасли в соответствии с полученными значениями искомых переменных величин в оптимальном плане:
| Предприятия | Варианты развития предприятий | Объем производства продукции, ед. |
Приведенные затраты, |
|
| 1–го вида | 2–го вида | |||
|
1 |
1 |
5 |
4 |
8 |
|
2 |
1 |
15 |
6 |
9 |
|
Итого: |
20 |
10 |
17 |
Список использованных источников
1. Экономико-математические методы и модели. Под ред. Кузнецова А.В. Минск, БГЭУ, 1999 г.
2. Математические методы в планировании отраслей и предприятий. Учебное пособие под ред. Попова И.Г. М., Экономика, 1981 г.
3. Терехов Л.Л. Экономико-математические методы. М., Статистика, 1972 г.