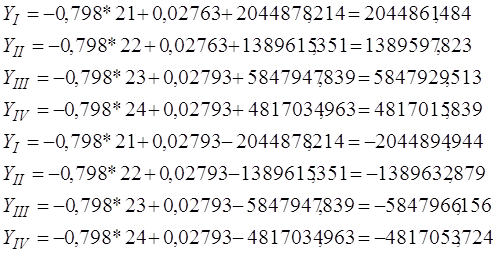Контрольная работа: Оптимальный план загрузки оборудования и транспортных связей
Раздел: Рефераты по экономико-математическому моделированию
Тип: контрольная работа
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ГОУ ВПО "МАРИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ"
Кафедра менеджмента и бизнеса
Расчетно-графическая работа
по дисциплине: "Моделирование экономических процессов"
Выполнила: студентка гр. МТ-32
Лескова С.Е.
Проверила: Руденко С.А.
Йошкар-Ола 2005
Задача загрузки оборудования
Завод железобетонных изделий изготовляет 4 вида панелей для типов жилых домов. Изделие производятся на 3-х группах взаимозаменяемого оборудования. Известны: фонд машинного времени и производственная программа по видам изделий. Требуется составить оптимальный план загрузки оборудования, т.е. так распределить работы по группам оборудования, чтобы общие издержки по производству панелей были минимальными. Исходные данные приведены в табличной форме:
| Изделие |
Производственная программа 100 - 500 |
Норма расходов ресурсов на производство единицы продукции (мин) | Издержки производства единицы продукции | ||||
| Группы технического оборудования | |||||||
| 1 | 2 | 3 | 1 | 2 | 3 | ||
| НС-А1 | 370 | 33 | 18 | 17 | 16,5 | 7,9 | 17,3 |
| НС-А2 | 230 | 12 | 31 | 30 | 12,4 | 14,2 | 15,4 |
| НС-А3 | 400 | 42 | 15 | 16 | 10,8 | 15,7 | 12,6 |
| НС-А4 | 360 | 27 | 37 | 25 | 20,3 | 11,1 | 14,2 |
| Объем ресурсов (часов) | 260 | 200 | 210 |
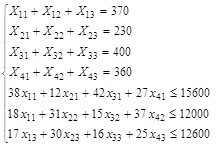
Z (х) = 16,5х11 + 7,9х12 + 17,3х13 + 12,4х21 + 14,2х22 +1 5,4х23 + 10,8х31 +15,7х32 + 12,6х33 + 20,3х41 + 11,1х42 + 14,2х43 стремится к минимуму. Пусть х11=х1, Х12=х2, Х13=х3,……., х43=х12.
Тогда
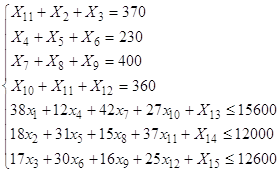
Z (х) = 16,5х1+ 7,9х2 + 17,3х3 + 12,4х4 +……. + 14,2х12 стремится к минимуму.
Введем искусственные переменные У1, У2, У3, У4
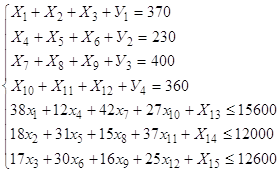
Z (х) = 16,5х1+ 7,9х2 + 17,3х3 + 12,4х4 +……. + 14,2х12 +М (У1+У2+У3+У4) стремится к минимуму,
где М - большое положительное число,
У1 = 370 - (х1+х2+х3)
У2 = 230 - (х4+х5+х6)
У3 = 360 - (х10+х11+х12)
Х13 = 15600 - (38х1 + 12х4 + 42х7 + 27х10)
Х14 = 12000 - (18х2 + 31х5 + 15х8 + 37х11)
Х15 = 12600 - (17х3 + 30х6 + 16х9 + 25х12)
(0,0,0,0….0; 15600; 12000; 370; 230; 400; 360) - это первое решение, которое мы получили. Z (х) = 16,5х1+ 7,9х2 + 17,3х3 + М (370-х1-х2-х3-+230-х4-х5-х6+400-х7-х8-х9+360-х10-х11-х12) =1360М- (м-16,5) х1- (м-7,9) Х2- (М-17,3) Х12 Стремится к минимуму.
Поскольку задача сведена к минимуму, то ведущий столбец выбираем по оптимально, если все числа в индексной строке будут меньше, либо равны.
Составим оптимальную таблицу:
|
Баз пер |
Зн. Пер. |
Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | Х7 | Х8 | Х9 | Х10 | Х11 | Х12 | Х13 | Х14 | Х15 | У1 | У2 | У3 | У4 |
| У1 | 370 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| У2 | 230 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| У3 | 400 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| У4 | 360 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Х13 | 15600 | 33 | 0 | 0 | 12 | 0 | 0 | 42 | 0 | 0 | 27 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Х14 | 12000 | 0 | 18 | 0 | 0 | 31 | 0 | 0 | 15 | 0 | 0 | 37 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| Х15 | 12600 | 0 | 0 | 17 | 0 | 0 | 30 | 0 | 0 | 16 | 0 | 0 | 25 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
|
Z |
12360 |
М-16,5 |
М-7,9 |
М-17,3 |
М-12,4 |
М-14,2 |
М-15,4 |
М-10,8 |
М-15,7 |
М-12,6 |
М-20,3 |
М-11,1 |
М-14,2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| Х2 | 370 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| У2 | 230 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| У3 | 400 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| У4 | 360 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Х13 | 15600 | 33 | 0 | 0 | 12 | 0 | 0 | 42 | 0 | 0 | 27 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Х14 | 12000 | 0 | 0 | 0 | 0 | 31 | 0 | 0 | 15 | 0 | 0 | 37 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| Х15 | 126000 | 0 | 0 | 17 | 0 | 0 | 30 | 0 | 0 | 16 | 0 | 0 | 25 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
|
Z |
990м+ 2923 |
-8,6 |
0 |
-9,4 |
М-12,4 |
М-14,2 |
М-15,4 |
М-10,8 |
М-15,7 |
М-12,6 |
М-20,3 |
М-11,1 |
М-14,2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| Х2 | 370 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| У2 | 230 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| Х7 | 400 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| У4 | 360 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Х13 | 15600 | 33 | 0 | 0 | 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Х14 | 12000 | 0 | 0 | 0 | 0 | 31 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| Х15 | 12600 | 0 | 0 | 17 | 0 | 0 | 30 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
|
Z |
590м +7243 |
-8,6 |
0 |
-9,4 |
М-12,4 |
М-14,2 |
М-15,4 |
0 |
М-15,7 |
М-12,6 |
М-20,3 |
М-11,1 |
М-14,2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| Х2 | 370 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| У2 | 230 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| Х7 | 400 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Х11 | 360 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Х13 | 15600 | 33 | 0 | 0 | 12 | 0 | 0 | 0 | 0 | 0 | 27 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Х14 | 1200 | 0 | 0 | 0 | 0 | 31 | 0 | 0 | 15 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| Х15 | 126001 | 0 | 0 | 17 | 0 | 0 | 30 | 0 | 0 | 16 | 0 | 0 | 25 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
|
Z |
230м +11239 |
-8,6 |
0 |
-9,4 |
М-12,4 |
М-14,2 |
М-15,4 |
0 |
-4,9 |
-1,8 |
-9,2 |
0 |
-3,1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| Х2 | 370 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Х4 | 230 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Х7 | 400 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Х11 | 360 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Х13 | 15600 | 33 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 27 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Х14 | 12000 | 0 | 0 | 0 | 0 | 31 | 0 | 0 | 15 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| Х15 | 12600 | 0 | 0 | 17 | 0 | 0 | 30 | 0 | 0 | 16 | 0 | 0 | 25 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
|
Z |
14091 |
-8,6 |
0 |
-9,4 |
0 |
-1,8 |
-3 |
0 |
-4,9 |
-1,8 |
-9,2 |
0 |
-9,1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1360М - ![]() = 1360М - 370М + 2923 =
990М + 2923 -
= 1360М - 370М + 2923 =
990М + 2923 - ![]() = 590М + 7243.
= 590М + 7243.
590М + 7243 - ![]() = 230М + 11239
= 230М + 11239
230М + 11239 - ![]() т = 14091
т = 14091
Для того, чтобы общие издержки по производству панелей были минимальными, нам необходимо сделать 230 железобетонных изделий НС - А2 вида и 94 железобетонных изделий НС - А3 вида, 370 железобетонных изделий вида НС - А1, 144 железобетонных изделий вида НС - А4.
Многоэтапная транспортная задача
Найти оптимальный план транспортных связей пунктов производства с перевалочными пунктами и перевалочных пунктов с потребителями готовой продукции, который бы обеспечил минимальные транспортные затраты, если имеются 4 пункта производства продукции, 4 перевалочных пункта, 4 пункта потребления готовой продукции.
|
Q1 |
Q2 |
Q3 |
Q4 |
B1 |
B2 |
B3 |
B4 |
B5 |
||
|
A1 |
5 | 0 | 125 | 0 | М | М | М | М | 0 | 130 |
|
A2 |
0 | 80 | 0 | 10 | М | М | М | М | 0 | 90 |
|
A3 |
10 | 0 | 0 | 80 | М | М | М | М | 0 | 90 |
|
A4 |
80 | 0 | 0 | 0 | М | М | М | М | 0 | 80 |
|
Q1 |
65 | М | М | М | 65 | 0 | 0 | 0 | 25 | 160 |
|
Q2 |
М | 0 | М | М | 0 | 75 | 5 | 0 | 0 | 80 |
|
Q3 |
М | М | 0 | М | 0 | 0 | 90 | 0 | 35 | 125 |
|
Q4 |
М | М | М | 0 | 0 | 0 | 0 | 90 | 0 | 90 |
| 160 | 80 | 125 | 90 | 65 | 75 | 95 | 95 | 60 |
X1=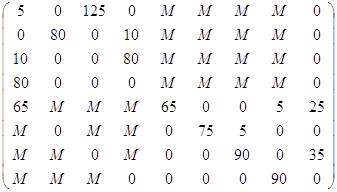
C = 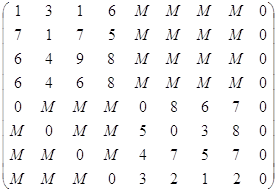
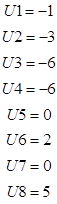
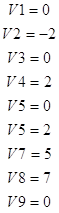
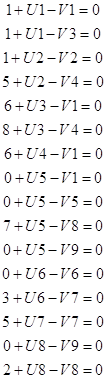
C1=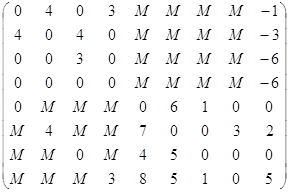
X1=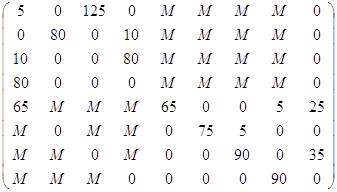
![]() min (25;
min (25;
10) =10
X2=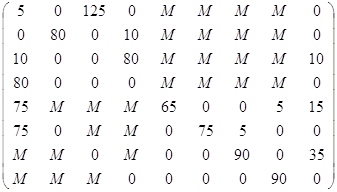
C=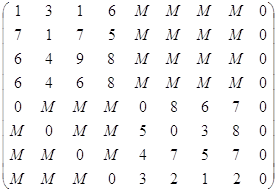
C2=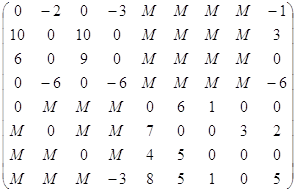
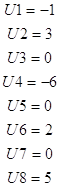
![]()
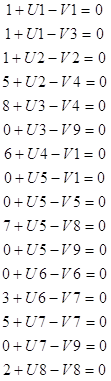
X2=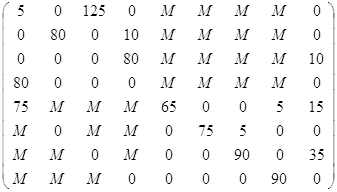
X3=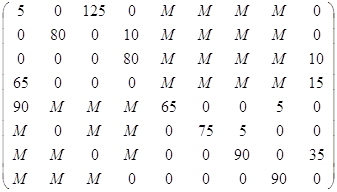
C=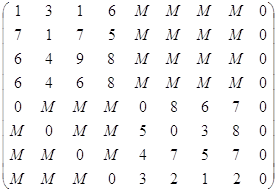
C3=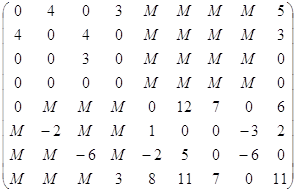
X3=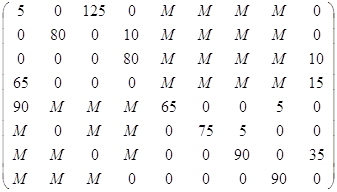
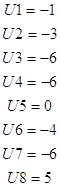

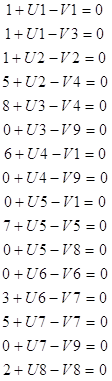
X3 (опт)
=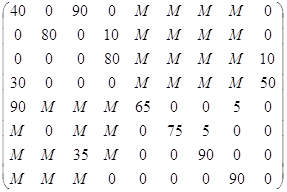
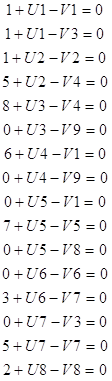
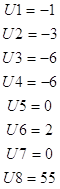
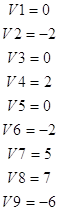
C=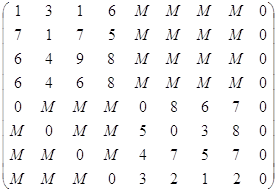
C4=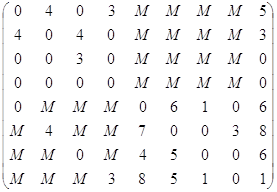
MIN Z =
40*1+90*1+80*1+10*5+80*8+10*0+30*6+50*0+90*0+65*0+5*7+75*0+5*3+35*0+90*5+90*5+90*2=1760
Вывод: от производителя до первого перевалочного пункта было доставлено 40 единиц товара, из первого пункта производства вывезено в 3-ий перевалочный пункт 00 единиц товара. Из 2-го пункта производства вывезено во 2-ой перевалочный пункт 80 единиц товара. Из 3-его пункта производства вывезено в 4-ый перевалочный пункт 80 единиц товара. Из 3-его пункта производства не вывезено 10 единиц товара. Из 4-ого пункта производства в 1-ый перевалочный пункт вывезено 30 единиц товара. Из 4-ого пункта производства не вывезено 50 единиц товара.
Из 1-го перевалочного пункта не вывезено 90 единиц товара. Из 1-го перевалочного пункта вывезено в 1-ый пункт производства 65 единиц товара. Из 1-го перевалочного пункта вывезено в 4-ый пункт производства 5 единиц товара. Из 2-го перевалочного пункта вывезено во 2-ой пункт производства 75 единиц товара. Из 2-го перевалочного пункта вывезено в 3-ий пункт производства 5 единиц товара. Из 3-го перевалочного пункта не вывезено 35 единиц товара. Из 3-го перевалочного пункта в 3-ий пункт производства вывезено 90 единиц товара. Из 4-го перевалочного пункта в 4-й пункт производства перевезено 90 единиц товара.
Парная корреляция
| Среднесписочная численность работников (X) | Затраты на производство продукции (Y) |
| 319 | 168.1 |
| 358 | 176.2 |
| 399 | 159.4 |
| 401 | 138.9 |
| 419 | 169.7 |
| 420 | 123.5 |
| 425 | 153.4 |
| 429 | 113.4 |
| 455 | 121.5 |
| 459 | 134.6 |
| 463 | 124.5 |
| 465 | 145.9 |
| 481 | 154.9 |
| 491 | 148.7 |
| 517 | 126.6 |
| 529 | 128.6 |
| 534 | 116.2 |
| 561 | 158.4 |
| 602 | 111.6 |
| 614 | 189.4 |
Определим количество интервалов каждого ряда, используя формулу Стэрджесса:
К=1+3,322*Lg0, К=1+3,322* Lg20 =5
Определим размах колебаний по ряду X и по ряду Y:
RX=Rmax-Rmin
Rx=614-319=295
RY=Rmax-Rmin
RY=189,4-111? 6=77,8
Определим длину интервала:
Lx=Rx/K=295/5=59
Lу=Rу/K=77,8/5=15,56
Определим значение рядов X и У
Min значение Y: 111,6- (15,56/2) =103,82
Min значение X: 319- (57,8/2) =290,1
Определим границы интервалов и частоты по рядам X и Y:
| № | Интервалы X | Частоты | № | Интервалы Y | частоты |
| 1 | 290,1-347,9 | 1 | 1 | 103,82-119,38 | 3 |
| 2 | 347,9-405,8 | 3 | 2 | 119,38-134,94 | 6 |
| 3 | 405,8-463,6 | 7 | 3 | 134,94-150,5 | 3 |
| 4 | 463,6-521,4 | 4 | 4 | 150,5-166,06 | 4 |
| 5 | 521,4-579,2 | 3 | 5 | 166,06-181,62 | 3 |
| 6 | 579,2-637 | 2 | 6 | 181,62-197,18 | 1 |
Построим поле корреляции
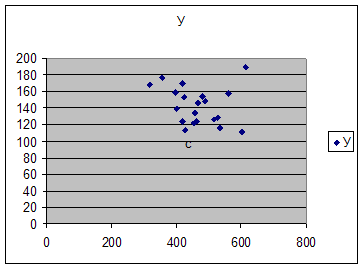
Для того, чтобы определить эмпирическую и теоретическую линейные регрессии построим корреляционную таблицу:
| 290,1-347,9 | 347,9-405,8 | 405,8-463,6 | 463,6-521,4 | 521,4-579,2 | 579,2-637 | частота |
|
|
| 103,82-119,38 | 1 | 1+1 | 3 | 531,03 | ||||
| 119,38-134,94 | 1+1+1+1 | 1 | 1 | 6 | 463,6 | |||
| 134,94-150,5 | 1 | 1+1 | 3 | 444,3 | ||||
| 150,5-166,06 | 1 | 1 | 1 | 1 | 4 | 463,59 | ||
| 166,06-181,62 | 1 | 1 | 1 | 3 | 376,09 | |||
| 181,62-197,18 | 1 | 1 | 376,85 | |||||
| частота | 1 | 3 | 7 | 4 | 3 | 2 | 20 | |
|
|
173,84 | 157,37 | 127,48 | 238,09 | 259,09 | 259,5 | 150,5 |
![]() =
=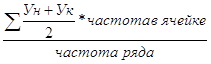
У1 = 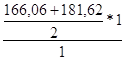 =173,84
=173,84
У2 = 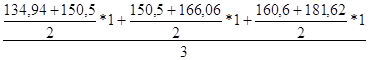 =157,37
=157,37
У3 = 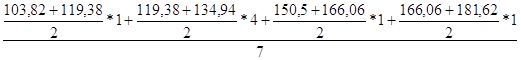 =127,48
=127,48
У4 = 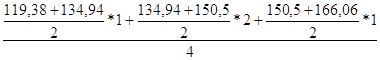 =238,09
=238,09
У5 = 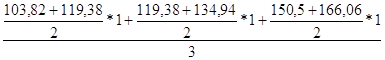 =259,5
=259,5
У6 = 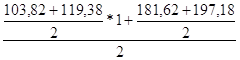 =150,5
=150,5
![]() =
=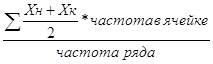
Х1 =  =531,03
=531,03
Х2 = 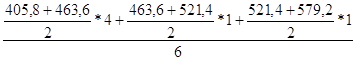 =463,6
=463,6
Х3 = 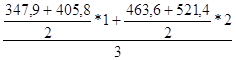 =444,3
=444,3
Х4 = 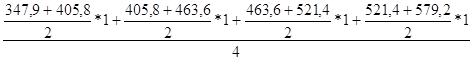 =463,59
=463,59
Х5 = 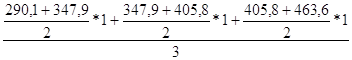 =376,85
=376,85
Х6 = ![]() =608,1
=608,1
Найдем уравнение регрессии
Y=ao+a1x
ao и a1 найдем из системы:
nao+a1![]() =
=![]()
ao![]() + a1
+ a1![]() =
=![]()
Построим расчетную таблицу:
| № | Х | У | X^2 | Y^2 | X*Y |
|
| 1 | 319 | 168,1 | 101761 | 28257,61 | 53623,9 | 151,97 |
| 2 | 358 | 176,2 | 128164 | 31046,44 | 63079,6 | 149,63 |
| 3 | 399 | 159,4 | 159201 | 25408,36 | 63600,6 | 147,17 |
| 4 | 401 | 138,9 | 160801 | 19293,21 | 55698,9 | 147,05 |
| 5 | 419 | 169,7 | 175561 | 28798,09 | 71104,3 | 145,97 |
| 6 | 420 | 123,5 | 176400 | 15252,25 | 51870 | 145,91 |
| 7 | 425 | 153,4 | 180625 | 23531,56 | 65195 | 145,61 |
| 8 | 429 | 113,4 | 184041 | 12859,56 | 48648,6 | 145,37 |
| 9 | 455 | 121,5 | 207025 | 14762,25 | 55282,5 | 143,87 |
| 10 | 459 | 134,6 | 210681 | 18117,16 | 61781,4 | 143,57 |
| 11 | 463 | 124,5 | 214369 | 15500,25 | 57643,5 | 143,33 |
| 12 | 465 | 145,9 | 216225 | 21286,81 | 67843,5 | 143,21 |
| 13 | 481 | 154,9 | 231361 | 23994,01 | 74506,9 | 142,25 |
| 14 | 491 | 148,7 | 241081 | 22111,69 | 73011,7 | 141,05 |
| 15 | 517 | 126,6 | 267289 | 16027,56 | 65452,2 | 140,09 |
| 16 | 529 | 128,6 | 279841 | 16537,96 | 68029,4 | 139,97 |
| 17 | 534 | 116,2 | 285156 | 13502,44 | 62050,8 | 139,07 |
| 18 | 561 | 158,4 | 314721 | 25090,56 | 88862,4 | 137,05 |
| 19 | 602 | 111,6 | 362404 | 12454,56 | 67183,2 | 134,99 |
| 20 | 614 | 189,4 | 376996 | 35872,36 | 116291,6 | 134,27 |
| Итого: | 9341 | 2863,5 | 4473703 | 419704,69 | 1330760 | 2861,74 |
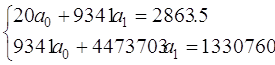
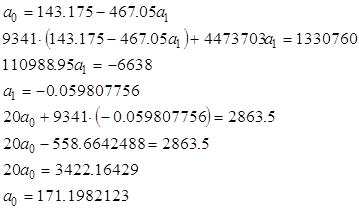
Таким образом, уравнение регрессии получается:
![]()
Используя уравнение регрессии, дополним последний столбец расчетной таблицей. Измерим частоту связи в парной корреляции с помощью коэффициента корреляции:
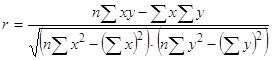
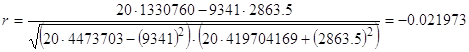
Вывод: коэффициент корреляции r равен - 0,02, что говорит о наличии прямой слабой связи между затратами на единицу продукции и балансовой прибыли предприятия.
Рассчитаем t-критерий Стьюдента:
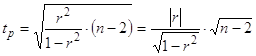
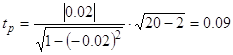
![]()
![]()
гипотеза о наличии прямой слабой связи между показателями не отвергается.
Прогнозирование сезонных явлений.
Построить прогнозную модель сезонного явления. Рассчитать показатели сезонности, используя скользящую среднюю и уравнение тренда. Рассчитать поквартальные индексы сезонности. Описать модели прогноза.
| Год | Квартал | Фактическое значение | Расчет с помощью экспоненциального сглаживания | Расчет по уравнению тренда | ||
| Расчетный уровень ряда | Показатели сезонности | Расчетный уровень ряда | Показатели сезонности | |||
| 1996 | I | 715 | -54987,9 | -0,01300287 | ||
| II | 2145 | 715 | 3 | -169116 | -0,01268359 | |
| III | 2955 | 1716 | 1,72203 | -233762 | -0,01264105 | |
| IV | 3822 | 2583,3 | 1,4795 | -302958 | -0,01261563 | |
| 1997 | I | 594 | 3450,39 | 0,17215 | -45330,8 | -0,01310366 |
| II | 2112 | 1450,917 | 1,45563 | -166482 | -0,01268602 | |
| III | 2156 | 1913,675 | 1,12663 | -169994 | -0,0126828 | |
| IV | 962 | 2083,303 | 0,46177 | -74700,9 | -0,01287802 | |
| 1998 | I | 126 | 1298,391 | 0,09704 | -7979,76 | -0,01578995 |
| II | 415 | 477,7172 | 0,86871 | -31044,9 | -0,01336776 | |
| III | 821 | 433,8152 | 1,89251 | -63447,7 | -0,01293979 | |
| IV | 1557 | 704,8446 | 2, 209 | -122188 | -0,01274267 | |
| 1999 | I | 198 | 1301,353 | 0,15215 | -13726,1 | -0,01442509 |
| II | 318 | 529,006 | 0,60113 | -23303,3 | -0,01364615 | |
| III | 1218 | 381,3018 | 3, 19432 | -95132,3 | -0,01280323 | |
| IV | 2415 | 966,9905 | 2,49744 | -190665 | -0,0126662 | |
| 2000 | I | 388 | 1980,597 | 0, 1959 | -28890 | -0,01343026 |
| II | 242 | 865,7791 | 0,27952 | -17237,7 | -0,01403898 | |
| III | 636 | 429,1337 | 1,48206 | -48682,9 | -0,01306415 | |
| IV | 970 | 573,9401 | 1,69007 | -75339,4 | -0,01287507 |
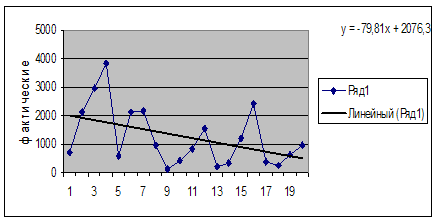
1,2) На основании исходных данных строим в MS Excel график с добавлением на него линии тренда. При построении тренда необходимо, чтобы на нем отобразилось уравнение тренда.
Графа 4 рассчитывается: при помощи поката анализа MS Excel с использованием функции экспоненциальное сглаживание.
Графа 5 рассчитывается: делением графы 3 на графу 4.
Графа 6 рассчитывается: подстановкой в уравнение линейного тренда, полученного при помощи MS Excel, соответствующих значений периода (от 1 до 20 по диаграмме).
Графа 7 рассчитывается: делением графы 3 на графу 6.
3) определяем индексы сезонности по кварталам, которые вычисляются по формуле:
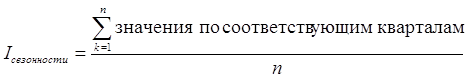
n - количество лет.
Индексы сезонности товарооборота
| Квартал | Индекс сезонности | ||
| С помощью экспоненциального сглаживания | С помощью уравнения тренда | ||
| I | 0,15431187 | -0,013950368 |
|
| II | 1,24099806 | -0,0132845 | |
| III | 1,88350851 | -0,012826201 | |
| IV | 1,66755568 | -0,012755519 |
4) Описание модели прогноза для каждого квартала:
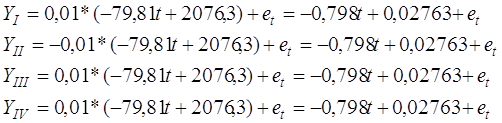
5) Расчет среднеквадратичного отклонения осуществляется с помощью следующей таблицы:
| Годы | I | II | III | IV | ||||||||
| факт | расчет | откл | факт | расчет | откл | факт | расчет | откл | факт | расчет | откл | |
| 1999 | 715 | 1996,49 | -1281,49 | 2145 | 1916,68 | 228,32 | 2955 | 1836,87 | 1118,13 | 3822 | 1757,06 | 2064,94 |
| 2000 | 594 | 1677,25 | -1083,25 | 2112 | 1597,44 | 514,56 | 2156 | 1517,63 | 638,37 | 962 | 1437,82 | -475,82 |
| 2001 | 126 | 1358,01 | -1232,01 | 415 | 1278, 20 | -863, 20 | 812 | 1198,39 | -386,39 | 1557 | 1118,58 | 438,42 |
| 2002 | 198 | 1038,77 | -840,77 | 318 | 958,96 | -640,96 | 1218 | 4496,95 | -3278,95 | 2415 | 799,34 | 1615,66 |
| 2003 | 318 | 719,53 | -401,53 | 242 | 639,72 | -397,72 | 636 | 559,91 | 76,09 | 970 | 3847,80 | -2877,80 |
При заполнении таблицы используются фактические данные и расчетные, полученные при помощи уравнения тренда.
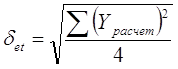
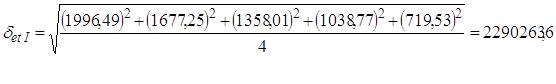
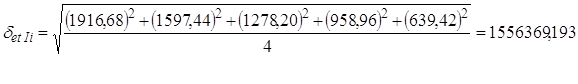
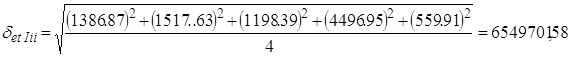
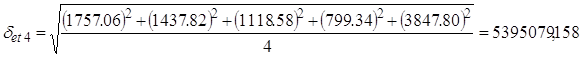
6) Расчет случайной величины:
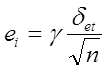
где ![]() =
2, n =5 (количество периодов, лет)
=
2, n =5 (количество периодов, лет)
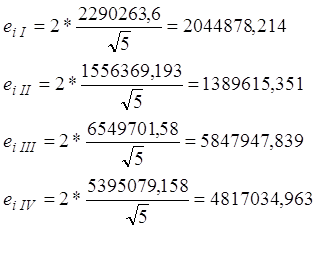
7) Построение прогноза на 2001 год
| I | II | III | IV | |
| нижняя | 1466,05 | 1106,17 | 2192,77 | 1901,45 |
| прогноз | 34,95 | 55,98 | 96,48 | 143,93 |
| верхняя | -1396,14 | -994, 20 | -1999,81 | -1613,60 |
Прогнозное значение получается путем подстановки соответствующих периодов (21, 22, 23, 24) в уравнение прогноза каждого квартала (пункт 4).
Верхняя граница получается путем подстановки в уравнение модели прогноза каждого квартала соответствующей случайной величины с положительным знаком.
Нижняя граница получается путем подстановки в уравнение модели прогноза каждого квартала соответствующей случайной величины с отрицательным знаком.