Контрольная работа: Исследование частотно-временных характеристик и структурных преобразований систем радиоавтоматики
Министерство образования и науки Украины
Севастопольский национальный технический университет
Кафедра Радиотехники
Расчетно-графическое задание №1
по дисциплине “Радиоавтоматика”
Исследование частотно-временных характеристик и структурных преобразований систем радиоавтоматики
Выполнила: ст. гр. Р-41д
Грибенщиков А.А.
Проверил: профессор
Бабуров Э.Д.
Севастополь
2008
Задание №1
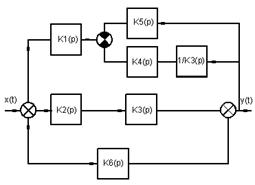
1.1 Для системы радиоавтоматики, схема которой приведена на рисунке 1, определить передаточные функции системы по управляющему сигналу и по помехе.
1.2 Для системы радиоавтоматики, схема которой приведена на рисунке 4, записать дифференциальное уравнение системы, определить аналитически и построить графически переходную и импульсную характеристики.
1.3 Построить амплитудно-фазовую характеристику разомкнутой системы.
1.4 Построить логарифмические амплитудно-частотную и фазо-частотную характеристики разомкнутой системы.
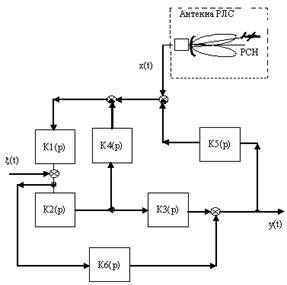
Рис. 1 – Структурная схема системы 1.
x(t) - входное управляющее воздействие;
y(t) - выходной регулируемый сигнал;
x(t)- помеха;
Кi(р) - передаточные функции звеньев системы
1.1 Для системы радиоавтоматики, схема которой приведена на рисунке 1, определим передаточные функции системы по управляющему сигналу и по помехе. Как известно, коэффициент передачи цепи, охваченной обратной связью, определяется по формуле
![]() (1)
(1)
где Кос(р) - коэффициент передачи обратной связи.
Передаточные функции звеньев системы 1 для данного варианта приведены в таблице 1.
Таблица 1 – Исходные данные
| № варианта | К1(р) | К2(р) | К3(р) | К4(р) | К5(р) | К6(р) |
|
8 |
р-2 |
р+1 |
(р+58)-1 |
17р+10 |
р |
р-2 |
Для удобства вычисления передаточной функции системы по управляющему сигналу упростим структурную схему системы 1 и изобразим её на рисунке 2. Упрощение произведём следующим образом: выходы звеньев 4 и 5 соединим и заведём на обратную (отрицательную) связь в одну точку. Также перенесём вход звена 4 с точки соединения звеньев 2 и 3 на выход звена 3 при этом переносе добавим последовательно перед входом звена 4 звено с передаточной функцией обратной К3(р).
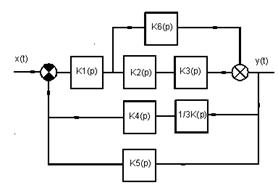 |
Рис. 2 – Упрощённая структурная схема системы 1(по управляющему сигналу)
Определим передаточную функцию системы 1 по управляющему сигналу.
![]() ,
, ![]()
![]()
К4![]() (р)=
(р)= ![]() К4
К4![]() 5(р)= К5(р)+
5(р)= К5(р)+![]()
Тогда передаточная функция системы 1 К(р) будет равна:
К(р)=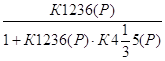
Подставив
значения К1236(р) и К4![]() 5(р) получим:
5(р) получим:
К(р)=
Подставим значения передаточных функций звеньев из таблицы 1, получим:
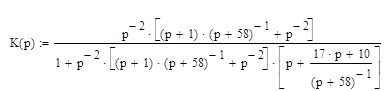
После упрощений, с использованием математического пакета MathCAD 2001 имеем:

 |
Определим передаточную функцию системы 1 по помехе, упрощенная структурная схема которой изображена на рисунке 3.
Рис. 3 – Упрощенная структурная схема
Очевидны следующие формулы:
![]()
![]()
![]()
![]()
Тогда с учетом (1) можно записать
![]()
Подставим значения передаточных функций звеньев из таблицы 1, тогда получим:
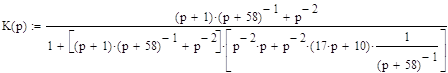
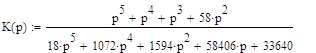
Для системы радиоавтоматики, схема которой приведена на рисунке 4 запишем дифференциальное уравнение системы, определим аналитически и построим графически переходную и импульсную характеристики.
Коэффициент передачи определяется по формуле
![]()

Рис. 4 — Структурная схема системы 2
Подставим значения передаточных функций звеньев из таблицы 1, тогда получим:


Напишем уравнение системы, на основании передаточной функции
![]()
где в скобках есть номер производной.
Определим переходную характеристику системы.
Переходная характеристика h(t) есть реакция динамического элемента на воздействие на воздействие в виде единичной ступенчатой функции 1(t):
![]()
![]()
где ![]() символ
обратного преобразования Лапласа.
символ
обратного преобразования Лапласа.
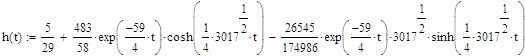
Определим импульсную характеристику системы:
Импульсная характеристика – это реакция динамического элемента на воздействие в виде d-функции:
![]()
Импульсная характеристика может быть определена как обратное преобразование Лапласа от передаточной функции динамического элемента:
![]()

Построим переходную и импульсную характеристики:
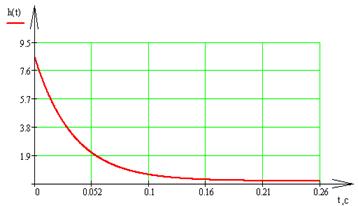
Рис. 5 – Переходная характеристика системы

Рис. 6 – Импульсная характеристика системы
3) Построить амплитудно-фазовую характеристику разомкнутой системы, схема которой приведена на рисунке 4.
Для перехода к разомкнутой системе преобразуем схему следующим образом:
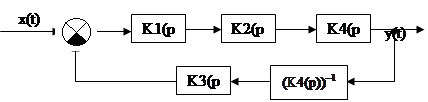
Разомкнув цепь обратной связи, получим:

Рис. 7 – Структурная схема разомкнутой системы
Определим передаточную функцию разомкнутой системы:
![]()
![]()
Заменим p на jw:
![]()
![]()
![]()
Построим график амплитудно-фазовой характеристики:

|
4) Построить логарифмические амплитудно-частотную и фазо-частотную характеристики разомкнутой системы, схема которой приведена на рисунке 4
Логарифмическая амплитудно-частотная характеристика определяется формулой:
![]()
Построим ЛАХ и ЛФХ:
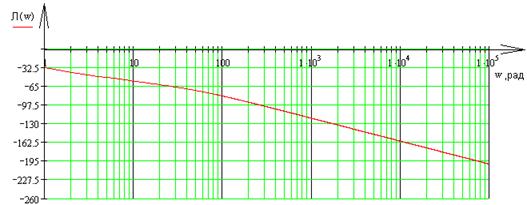
Рис. 9 – ЛАХ системы
