Реферат: Классификация помехоустойчивых кодов. Особенности практического кодирования
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
кафедра РЭС
реферат на тему:
«Классификация помехоустойчивых кодов. Особенности практического кодирования»
МИНСК, 2009
КРАТКАЯ КЛАССИФИКАЦИЯ ПОМЕХОУСТОЙЧИВЫХ КОДОВ
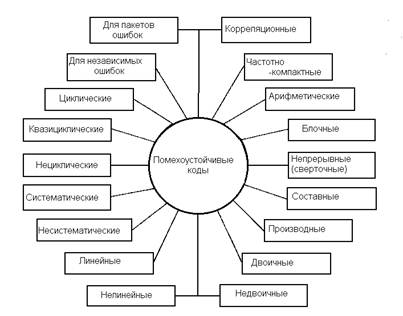
Рис 1. Классификация помехоустойчивых кодов
К настоящему времени разработано много различных помехоустойчивых кодов, отличающихся друг от друга основанием, расстоянием, избыточностью, структурой, функциональным назначением, энергетической эффективностью, корреляционными свойствами, алгоритмами кодирования и декодирования, формой частотного спектра. На рисунке, представленном выше, приведены типы кодов, различающиеся по особенностям структуры, функциональному назначению, физическим свойствам кода как сигнала.
Наиболее важный подкласс непрерывных кодов образуют сверточные коды, отличающиеся от других непрерывных кодов методом построения и более широкой областью применения.
В общем случае, чем длиннее код при фиксированной избыточности, тем больше расстояние и тем выше помехоустойчивость кода. Однако длинные коды сложно реализуются. Составные коды дают компромиссное решение задачи; из них основное значение имеют каскадные коды и коды произведения. Как правило, каскадный код состоит из двух ступеней (каскадов): внутренней и внешней. По линии связи сигналы передают внутренним кодом nвт, символьные слова которого являются символами внешнего кода длины nвш. Основание внешнего кода равно qвтk.
Коды произведения строят в виде матрицы, в которой строки суть слова одного кода, а столбцы - того же или другого кода.
При формировании каскадного кода входную информационную последовательность символов разбивают на блоки по kвт символов в каждом, каждый блок сопоставляют с информационным символом внешнего кода из алфавита, содержащего qвтk значений символов. Затем kвш информационных символов внешнего кода преобразуют в блоки из nвш символов внешнего кода и, наконец, блоки из kвт информационных символов внутреннего кода преоб-разуют в блоки из nвт символов внутреннего кода. Возможны различные варианты: внешний и внутренний коды - блочные, внешний блочный - внутренний сверточный, внешний сверточный - внутренний блочный, внешний и внутренний сверточные.
Один из наиболее распространенных методов формирования кода произведения заключается в последовательной записи по k1 символов входной информационной последовательности в k2 строк матрицы (например, в ячейки памяти ОЗУ), добавлении избыточных символов по n1-k1 в каждую строку и по n2-k2 в каждый столбец, после чего в последовательность символов кода считывают по строкам или столбцам из матрицы. Физическим аналогом кода произведения является, в частности, частотно-временной код, у которого строки располагаются вдоль оси времени, а столбцы - по оси частот.
Параметры составных кодов: каскадных - n=nвшnвт, k=kвшkвт, d=dвшdвт; произведения - n=n1n2, k=k1k2, d=d1d2.
Производные коды строят на основе некоторого исходного кода, к которому либо добавляют символы, увеличивая расстояние (расширенный код), либо сокращают часть информационных символов без изменения расстояния (укороченный код), либо выбрасывают (выкалывают) некоторые символы (выколотый, или перфорированный код). Код Хэмминга дает пример процедуры расширения, увеличивающей расстояние кода с 3 до 4. Необходимость в выкалывании возникает в результате построения на основе исходного кода другого, менее мощного, более короткого кода с тем же расстоянием.
При более широкой трактовке термина "производный код" к этому классу можно отнести все коды, полученные из исходного добавлением или исключением как символов, так и слов.
Формально деление кодов на двоичные и недвоичные носит искусственный характер; по аналогии следует выделять троичные, четверичные и другие коды большего основания. Оправдывается такое деление усложнением алгоритмов построения, кодирования и декодирования недвоичных кодов.
При прочих равных условиях желательно, чтобы информационные и избыточные символы располагались отдельно. В систематических кодах это условие выполняется.В циклических кодах каждое слово содержит все свои циклические перестановки. Все n циклических перестановок (слова длины n) образуют цикл. В квазициклических кодах цикл образуется на числе символов n-1 или, реже, n-2. Циклические коды важны как с точки зрения математического описания, так и для построения и реализации кода.
Ошибки в каналах связи имеют самое различное распределение, однако для выбора помехоустойчивого кода целесообразно разделить все возможные конфигурации ошибок на независимые (некоррелированные) и пакеты (коррелированные ошибки). На практике приходится учитывать качество интервалов между пакетами: они могут быть свободными от ошибок или же содержать случайные независимые ошибки.
Под корреляционными подразумевают коды, обладающие хорошими корреляционными свойствами, важными при передаче сигналов вхождения в связь, для повышения защищенности от некоторых видов помех, извлечения сигналов из интенсивных шумов, обеспечения многостанционного доступа, построения асинхронно-адресных систем связи. Корреляционные коды включают в себя пары противоположных сигналов с хорошей функцией автокорреляции (метод внутриимпульсной модуляции), импульсно-интервальные коды, имеющие на фиксированном интервале времени постоянное для всех слов кода число импульсов с неперекрывающимися (при любом взаимном сдвиге слов во времени) значениями интервалов между импульсами, ансамбли сигналов с хорошими взаимокорреляционными свойствами.
Особый класс образуют частотно-компактные коды, предназначенные для сосредоточения энергии сигнала в возможно более узкой полосе частот. Столь общая постановка задачи понимается в различных системах связи по-разному: в проводных линиях и линейных трактах, содержащих полосно-ограничивающие фильтры с крутыми фронтами, необходимо основную энергию сигналa "отодвинуть" от крайних частот к центру полосы пропускания целью уменьшения межсимвольных искажений; в сетях радиосвязи с жесткими ограничениями по электромагнитной совместимости радиосредств от кода требуется значительно (на десятки децибел) уменьшить уровень внеполосных излучений. Построение кодирование и декодирование частотно-компактных кодов существенно зависят от метода модуляции.
Арифметические коды служат для борьбы с ошибками при вы полнении арифметических операций в процессоре ЭВМ.
Далее рассматриваются два типа кодов: блоковые и древовидные. Определяющее различие между кодерами для кодов этих двух типов состоит в наличии или отсутствии памяти. Кодер для блокового кода является устройством без памяти, отображающим последовательности из k входных символов в последовательности из n выходных символов. Термин "без памяти" указывает, что каждый блок из n символов зависит только от соответствующего блока из k символов и не зависит от других блоков. Это не означает, что кодер не содержит элементов памяти. Важными параметрами блокового кода являются n, k, R=k/n и dmin. На практике значения k лежат между 3 и несколькими сотнями, a R= =1/4 ...7/8. Значения, лежащие вне этих пределов, являются возможными, но часто приводят к некоторым практическим трудностям. Входные и выходные последовательности обычно состоят из двоичных символов, но иногда могут состоять из элементов некоторого алфавита большего объема. Кодер для древовидного кода является устройством с памятью, в которое поступают наборы из m двоичных входных символов, а на выходе появляются наборы из n двоичных выходных символов. Каждый набор n выходных символов зависит от текущего входного набора и от v предыдущих входных символов. Таким образом, память кодера должна содержать v+m входных символов. Параметр v+m часто называют длиной кодового ограничения данного кода и обозначают k=v+m (не следует путать с параметром k для блокового кода). Отметим, что обозначения часто не согласуются друг с другом. Некоторые авторы называют длиной кодового ограничения параметр k, в то время как другие - параметр v. Здесь длиной кодового ограничения будем называть величину v, поскольку это приводит к меньшей путанице для кодов с m>1. Параметр k=v+m почти не будет использоваться. Древовидные коды характеризуются также скоростью R=m/n и свободным расстоянием dсв. Точное определение dсв более громоздко, чем определение dmin для блоковых кодов, однако параметр dсв, по существу, содержит ту же информацию о коде, что и dmin. Типичные значения параметров древовидных кодов таковы: m, n=1...8, R= 1/4... 7/8, v=2...60.
При другом подходе коды можно разделить на линейные и нелинейные. Линейные коды образуют векторное пространство и обладают следующим важным свойством: два кодовых слова можно сложить, используя подходящее определение суммы, и получить третье кодовое слово. В случае обычных двоичных кодов эта операция является посимвольным сложением двух кодовых слов по модулю 2 (т. е. 1+1=0, 1+0=1, 0+0=0). Это свойство приводит к двум важным следствиям. Первое из них состоит в том, что линейность существенно упрощает процедуры кодирования и декодирования, позволяя выразить каждое кодовое слово в виде "линейной" комбинации небольшого числа выделенных кодовых слов, так называемых базисных векторов. Второе свойство состоит в том, что линейность существенно упрощает задачу вычисления параметров кода, поскольку расстояние между двумя кодовыми словами при этом эквивалентно расстоянию между кодовым словом, состоящим целиком из нулей, и некоторым другим кодовым словом. Таким образом, при вычислении параметров линейного кода достаточно рассмотреть, что происходит при передаче кодового слова, состоящего целиком из нулей. Вычисление параметров упрощается еще и потому, что расстояние Хемминга между данным кодовым словом и нулевым кодовым словом равно числу ненулевых элементов данного кoдового слова. Это число часто называют весом Хемминга данного слова, и список, содержащий число кодовых слов каждого веса, можно использовать для вычисления характеристик кода с помощью аддитивной границы. Такой список называют спектром кода.
Линейные коды отличаются от нелинейных замкнутостью кодового множества относительно некоторого линейного оператора, например сложения или умножения слов кода, рассматриваемых как векторы пространства, состоящего из кодовых слов - векторов. Линейность кода упрощает его построение и реализацию. При большой длине практически могут быть использованы только линейные коды. Вместе с тем часто нелинейные коды обладают лучшими параметрами по сравнению с линейными. Для относительно коротких кодов сложность построения и реализации линейных и нелинейных кодов примерно одинакова.
Как линейные, так и нелинейные коды образуют обширные классы, содержащие много различных конкретных видов помехоустойчивых кодов. Среди линейных блочных наибольшее значение имеют коды с одной проверкой на четность, M-коды (симплексные), ортогональные, биортогональные, Хэмминга, Боуза-Чоудхури-Хоквингема, Голея, квадратично-вычетные (KB), Рида-Соломона. К нелинейным относят коды с контрольной суммой, инверсные, Нордстрома-Робинсона (HP), с постоянным весом, перестановочные с повторением и без повторения символов (полные коды ортогональных таблиц, проективных групп, групп Матье и других групп перестановок).
Почти все схемы кодирования, применяемые на практике, основаны на линейных кодах. Двойные линейные блоковые коды часто называют групповыми кодами, поскольку кодовые слова образуют математическую структуру, называемую группой. Линейные древовидные коды обычно называют сверточными кодами, поскольку операцию кодирования можно рассматривать как дискретную свертку входной последовательности с импульсным откликом кодера.
Наконец, коды можно разбить на коды, исправляющие случайные ошибки, и коды, исправляющие пакеты ошибок. В основном мы будем иметь дело с кодами, предназначенными для исправления случайных, или независимых, ошибок. Для исправления пакетов ошибок было создано много кодов, имеющих хорошие параметры. Однако при наличии пачек ошибок часто оказывается более выгодным использовать коды, исправляющие случайные ошибки, вместе с устройством перемежения восстановления. Такой подход включает в себя процедуру перемешивания порядка символов в закодированной последовательности перед передачей и восстановлением исходного порядка символов после приема с тем, чтобы рандомизировать ошибки, объединенные в пакеты.
Особенности практического кодирования
Предположим, что все представляющие интерес данные могут быть представлены в виде двоичной (закодированной двоично) информации, т. е. в виде последовательности нулей и единиц. Задача формулируется стандартно. Эта двоичная информация подлежит передаче по каналу, подверженному случайным ошибкам. Задача кодирования состоит в таком добавлении к информационным символам дополнительных символов, чтобы на приемнике эти искажения могли быть найдены и исправлены. Иначе говоря, последовательность символов данных представляется в виде некоторой более длинной последовательности символов, избыточность которой достаточна для защиты данных.
Двоичный код мощности М и длины n представляет собой множество из М двоичных слов длины n, называемых кодовыми словами. Обычно М = 2k, где k - некоторое целое число; такой код называется двоичным (n,k)-кодом.
Например, можно построить следующий код: 10101 10010 01110 11111 Это очень бедный (и очень маленький) код с M = 4 и n=5, но он удовлетворяет приведенному выше определению. Данный код можно использовать для представления 2-битовых двоичных чисел, используя следующее (произвольное) соответствие:
00<-> 10101, 01<-> 10010, 10<-> 01110, 11<-> lllll.
Если получено одно из четырех 5-битовых кодовых слов, то полагаем, что соответствующие ему два бита являются правильной информацией. Если произошла ошибка, то мы получим 5-битовое слово, отличающееся от кодовых слов. Тогда попытаемся найти наиболее вероятно переданное слово и возьмем его в качестве оценки исходных двух битов информации. Например, если мы приняли 01100, то полагаем, что передавалось 01110, и, следовательно, информационное слово равнялось 10.
В приведенном примере код не является хорошим, так как он не позволяет исправлять много конфигураций ошибок. Желательно выбирать коды так, чтобы каждое кодовое слово по возможности больше отличалось от каждого другого кодового слова; в частности, это желательно в том случае, когда длина блока велика.
Mожет показаться, что достаточно определить требования к "хорошему коду" и затем предпринять машинный поиск по множеству всех возможных кодов. Но сколько кодов существует для данных n и k? Каждое кодовое слово представляет собой последовательность n двоичных символов, и всего имеется 2k таких слов; следовательно, код описывается n2k двоичными символами. Всего существует 2n2k способов выбора этих двоичных символов; следовательно, число различных (n,k)-кодов равно этому числу. Конечно, очень многие из этих кодов не представляют интереса (как в случае, когда два кодовых слова равны), так что надо либо проверять это по ходу поиска, либо развить некоторую теорию, позволяющую исключить такие коды.
Например, выберем (n,k) = (40,20) - код, весьма умеренный по современным стандартам. Тогда число таких кодов превзойдет величину 1010000000 - невообразимо большое число! Следовательно, неорганизованные процедуры поиска бессильны.
В общем случае блоковые коды определяются над произвольным конечным алфавитом, скажем над алфавитом из q символов {0, 1, 2, ..., q - 1}. На первый взгляд введение алфавитов, отличных от двоичного, может показаться излишним обобщением. Из соображений эффективности, однако, многие современные каналы являются недвоичными, и коды для этих каналов должны быть недвоичными. На самом деле коды для недвоичных каналов часто оказываются достаточно хорошими, и сам этот факт может служить причиной для использования недвоичных каналов. Двоичные данные источника тривиальным образом представляются символами q-ичного алфавита, особенно если q равно степени двойки, как это обычно и бывает на практике.
Определение. Блоковый код мощности М над алфавитом из q символов определяется как множество из М (q-ичных последо-вательностей длины q, называемых кодовыми, словами.
Если q = 2, то символы называются битами. Обычно М = qk для некоторого целого k, и мы будем интересоваться только этим случаем, называя код (n,k)-кодом. Каждой последовательности из k q-ичных символов можно сопоставить последовательность из n q-ичных символов, являющуюся кодовым словом.
Имеются два основных класса кодов: блоковые коды и древовидные коды; они иллюстрируются рис. 1. Блоковый код задает блок из k информационных символов n-символьным кодовым словом. Скорость R блокового кода определяется равенством R = k/n.(Скорость - величина безразмерная или, возможно, измеряемая в единицах бит/бит или символ/символ. Ее следует отличать от другого называемого тем же термином скорость понятия, измеряющего канальную скорость в бит/с. Используется и другое определение скорости: R = (k/n)logeq, единицей которого является нат/символ, где один нат равен log2e битов. Принято также определение R = (k/n) log2q, в котором скорость измеряется в единицах бит/символ.)
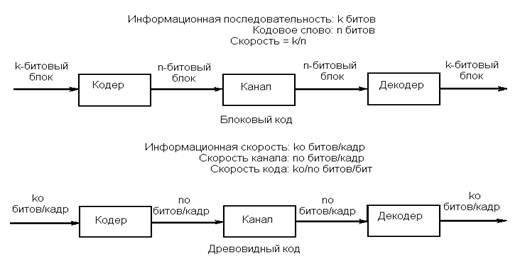
Рис. 2. Основные классы кодов.
Древовидный код более сложен. Он отображает бесконечную последовательность информационных символов, поступающую со скоростью k0 символов за один интервал времени, в непрерывную последовательность символов кодового слова со скоростью n0 символов за один интервал времени. Cосредоточим внимание на блоковых кодах.
Если сообщение состоит из большого числа битов, то в принципе лучше использовать один кодовый блок большой длины, чем последовательность кодовых слов из более короткого кода. Природа статистических флуктуаций такова, что случайная конфигурация ошибок обычно имеет вид серии ошибок. Некоторые сегменты этой конфигурации содержат больше среднего числа ошибок, а некоторые меньше. Следовательно, при одной и той же скорости более длинные кодовые слова гораздо менее чувствительны к ошибкам, чем более короткие кодовые слова, но, конечно, соответствующие кодер и декодер могут быть более сложными. Например, предположим, что 1000 информационных битов передаются с помощью (воображаемого) 2000-битового двоичного кода, способного исправлять 100 ошибок. Сравним такую возможность с передачей одновременно 100 битов с помощью 200-битового кода, исправляющего 10 ошибок на блок. Для передачи 1000 битов необходимо 10 таких блоков. Вторая схема также может исправлять 100 ошибок, но лишь тогда, когда они распределены частным образом - по 10 ошибок в 200-битовых подблоках. Первая схема может исправлять 100 ошибок независимо от того, как они расположены внутри 2000-битового кодового слова. Она существенно эффективнее.
Эти эвристические рассуждения можно обосновать теоретически, но здесь мы к этому не стремимся. Мы только хотим обосновать тот факт, что хорошими являются коды с большой длиной блока и что очень хорошими кодами являются коды с очень большой длиной блока. Такие коды может быть очень трудно найти, а будучи найденными, они могут потребовать сложных устройств для реализации операций кодирования и декодирования.
О блоковом коде судят по трем параметрам: длине блока n, информационной длине k и минимальному расстоянию d*. Минимальное расстояние является мерой различия двух наиболее похожих кодовых слов. Минимальное расстояние вводится двумя следующими определениями.
Определение. Расстоянием по Хэммингу между двумя q-ичными последовательностями х и у длины n называется число позиций, в которых они различны. Это расстояние обозначается через d(х, у).
Например, возьмем х = 10101 и у =01100; тогда имеем d (10101, 01100) = 3. В качестве другого примера возьмем х = 30102 и у = 21103; тогда d (30102, 21103) = 3.
Определение. Пусть C = {сi , i = 0, ..., М - 1} - код. Тогда минимальное расстояние кода C равно наименьшему из всех расстояний по Хэммингу между различными парами кодовых слов, т. е.
d* = min d(ci,сj).
(n, k)-код с минимальным расстоянием d* называется также (n, k, d*)-кодом.
В коде C, выбранном в примере, d (10101, 10010) =3, d (10010, 01110) = 3, d(10101, 01110) = 4, d(10010, 11111) == 3, d (10101, 11111) =2, d(01110, 11111) =2; следовательно, для этого кода d* = 2.
Предположим, что передано кодовое слово и в канале произошла одиночная ошибка. Тогда принятое слово находится на равном 1 расстоянии по Хэммингу от переданного слова. В случае, когда расстояние до каждого другого кодового слова больше чем 1, декодер исправит ошибку, если положит, что действительно переданным словом было ближайшее к принятому кодовое слово.
В более общем случае если произошло t ошибок и если расстояние от принятого слова до каждого другого кодового слова больше t, то декодер исправит эти ошибки, приняв ближайшее к принятому кодовое слово в качестве действительно переданного. Это всегда будет так, если
d* >= 2t + 1.
Иногда удается исправлять конфигурацию из t ошибок даже тогда, когда это неравенство не удовлетворяется. Однако если d* < 2t + 1, то исправление любых t ошибок не может быть гарантировано, так как тогда оно зависит от того, какое слово передавалось и какова была конфигурация из t ошибок внутри блока.
Геометрическая иллюстрация дается на рис. 3.4.
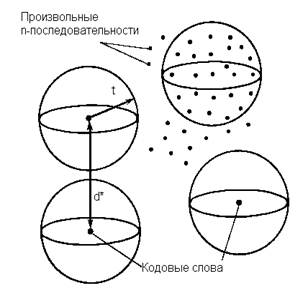
Рис. 3.4. Сферы декодирования.
В пространстве всех (q-ичных n-последовательностей выбрано некоторое множество n-последовательностей, объявленных кодовыми словами. Если d* - минимальное расстояние этого кода, а t - наибольшее целое число, удовлетворяющее условию d*>= 2t + 1, то вокруг каждого кодового слова можно описать непересекающиеся сферы радиуса t. Принятые слова, лежащие внутри сфер, декодируются как кодовое слово, являющееся центром соответствующей сферы. Если произошло не более t ошибок, то принятое слово всегда лежит внутри соответствующей сферы и декодируется правильно.
Некоторые принятые слова, содержащие более t ошибок, попадут внутрь сферы, описанной вокруг другого кодового слова, и будут декодированы неправильно. Другие принятые слова, содержащие более t ошибок, попадут в промежуточные между сферами декодирования области. В зависимости от применения последний факт можно интерпретировать одним из двух способов.
Неполный декодер декодирует только те принятые слова, которые лежат внутри сфер декодирования, описанных вокруг кодовых слов. Остальные принятые слова, содержащие более допустимого числа ошибок, декодер объявляет нераспознаваемыми. Такие конфигурации ошибок при неполном декодировании называются неисправляемыми. Большинство используемых декодеров являются неполными декодерами. Полный декодер декодирует каждое принятое слово в ближайшее кодовое слово. Геометрически это представляется следующим образом: полный декодер разрезает промежуточные области на куски и присоединяет их к сферам так, что каждая точка попадает в ближайшую сферу. Обычно некоторые точки находятся на равных расстояниях от нескольких сфер; тогда одна из этих сфер произвольно объявляется ближайшей. Если происходит более t ошибок, то полный декодер часто декодирует неправильно, но бывают и случаи попадания в правильное кодовое слово. Полный декодер используется в тех случаях, когда лучше угадывать сообщение, чем вообще не иметь никакой его оценки. Можно также рассматривать каналы, в которых кроме ошибок происходят и стирания. Это значит, что конструкцией приемника предусмотрено объявление символа стертым, если он получен ненадежно или если приемник распознал наличие интерференции или сбой. Такой канал имеет входной алфавит мощности q выходной алфавит мощности q + 1; дополнительный символ называется стиранием. Например, стирание символа 3 в сообщении 12345 приводит к слову 12-45. Это не следует путать с другой операцией, называемой выбрасыванием, которая дает 1245.
B таких каналах могут использоваться коды, контролирующие ошибки. В случае когда минимальное расстояние кода равно d*, любая конфигурация из р стираний может быть восстановлена, если d* >= р + 1. Далее, любая конфигурация из v ошибок и р стираний может быть декодирована при условии, что
d* >= 2v + 1 + р.
Для доказательства выбросим из всех кодовых слов те р компонент, в которых приемник произвел стирания. Это даст новый код, минимальное расстояние которого не меньше d* - р; следовательно, v ошибок могут быть исправлены при условии, что выполняется выписанное выше неравенство. Таким образом, можно восстановить укороченное кодовое слово с р стертыми компонентами. Наконец, так как d* > р + 1, существует только одно кодовое слово, совпадающее с полученным в нестертых компонентах; следовательно, исходное кодовое слово может быть восстановлено.
ЛИТЕРАТУРА
1. Лидовский В.И. Теория информации. - М., «Высшая школа», 2002г. – 120с.
2. Метрология и радиоизмерения в телекоммуникационных системах. Учебник для ВУЗов. / В.И.Нефедов, В.И.Халкин, Е.В.Федоров и др. – М.: Высшая школа, 2001 г. – 383с.
3. Цапенко М.П. Измерительные информационные системы. - . – М.: Энергоатом издат, 2005. - 440с.
4. Зюко А.Г. , Кловский Д.Д., Назаров М.В., Финк Л.М. Теория передачи сигналов. М: Радио и связь, 2001 г. –368 с.
5. Б. Скляр. Цифровая связь. Теоретические основы и практическое применение. Изд. 2-е, испр.: Пер. с англ. – М.: Издательский дом «Вильямс», 2003 г. – 1104 с.