Лабораторная работа: Математические модели окружающей среды
Практическая работа
по курсу «Математические модели окружающей среды»
Задано временное изменение уровня воды в некоторых пунктах за период примерно в 170 лет.
Применить методы математической статистики для оценки характеристик и качества имеющихся данных наблюдений. Выполнить прогноз подъема уровня воды на будущее и проверить качество прогноза на уже имеющихся данных.
1. Рассчитать моменты ряда (среднее и среднеквадратичное значение), построить функцию распределения и плотность функции распределения. Выполнить ее аппроксимацию теоретическими зависимостями.

Рис. 1.1. Изменение уровня воды за период в 102 года
Минимальный уровень воды = 0.06328, максимальное значение уровня = 0.6792
Заменим простой статистический ряд на статистический ряд с меньшим числом слагаемых, равным 100. И для такого ряда рассчитаем частоту события (в качестве события берем средний уровень воды).
Таким образом, имеем 100 интервалов, для каждого вычисляется частота события (число событий в статистическом ряде, когда X = x, к общему числу событий)
![]() .
.
В нашем случае имеем N=1024 события, а m – число уровней, попавших i-ый интервал Очевидны свойства этой частоты
![]()
Частоту различных уровней воды можно изобразить графически
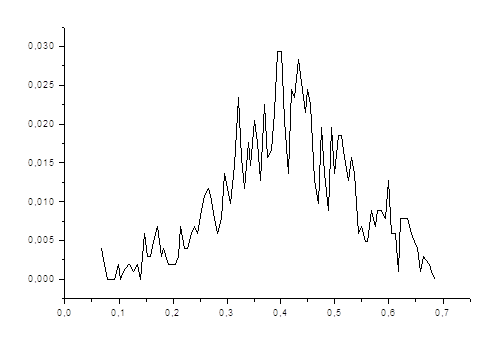
Рис. 1.2. График зависимости частоты от среднего уровня воды
Статистическая функция распределения есть «частота» события Х < x в данном статистическом интервале
![]() .
.

![]()
![]() Рис. 1.3. Функция
распределения
Рис. 1.3. Функция
распределения
![]() Эта функция F*(x) является
неубывающей со следующими пределами:
Эта функция F*(x) является
неубывающей со следующими пределами:
![]() F*(x ® –¥) = 0, F*(x ® + ¥) = 1.
F*(x ® –¥) = 0, F*(x ® + ¥) = 1.
С функцией распределения F(x) связана плотность функции распределения f(x)
![]() .
.
которая удовлетворяет следующим соотношениям:
f(x) ³ 0, ò f(x) dx = 1,
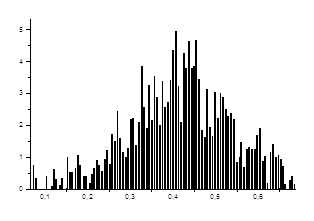
Рис. 1.4. Плотность функции распределения
Была выполнена аппроксимация плотности функции распределения теоретическими зависимостями: полиномами 6-ой, 9-ой, 15-ой степени, тригонометрическими многочленами. Оптимальным приближением оказался полином 9-ой степени.
В качества критерия оптимальной аппроксимации использовали критерий Пирсона
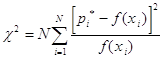
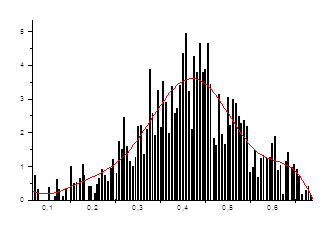
Рис. 1.5. Аппроксимация плотность функции распределения полиномом 9-ой степени
Для нового ряда по имеющимся данным можно рассчитать математическое ожидание, характеризующее среднее значение уровня воды
![]() ,
,
и среднеквадратичное отклонение, характеризующее средний разброс этих значений:
s*=![]() .
.
где ![]() - дисперсия:
- дисперсия:
![]()
xi – среднее значение случайной величины внутри разряда.
В нашем случае, средний уровень воды равен 0.41, а среднеквадратичное отклонение – 0.119
2. В какой степени данный ряд является стационарным? На каких временах данный ряд можно считать стационарным? Дать оценки моментов для «кусков» ряда и построить гистограммы оценок
Для того чтобы ряд был стационарным, должны быть выполнены условия
- корреляционная функция не зависит от времени
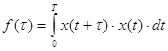
математическое ожидание ![]()
-
дисперсия
![]()
-
Для проверки стационарности делим исходный ряд на ![]() кусков, и для каждого
такого куска проверяем выполнение трех условий.
кусков, и для каждого
такого куска проверяем выполнение трех условий.
– Корреляционная функция.
Фиксируем ![]() , где N – количество точек.
, где N – количество точек.
Считаем автокорреляционную функцию для первого отрезка, а
затем – корреляционную функцию для каждых двух соседних кусков. Получаем
значение корреляционной функции при фиксированном ![]() для каждого куска ряда.
для каждого куска ряда.
Если процесс стационарный, то все значения должны совпадать со значением автокорреляционной функции.
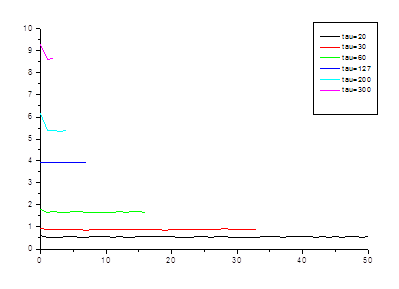
Рис. 2.1. Графики зависимости корреляционной функции от
номера отрезка при различных ![]() .
.
В качестве оценки корреляционной функции вычислили среднеквадратичное отклонение от значения автокорреляционной функции.
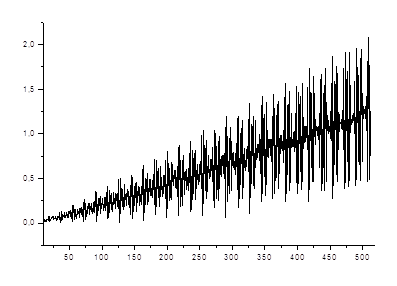
Рис. 2.2. Зависимость среднеквадратичного отклонения от ![]()
– Математическое ожидание
Для каждого «куска» ряда вычисляется математическое ожидание ![]() (
(![]() ;
; ![]() ). Затем находим среднее от
). Затем находим среднее от
![]() и среднеквадратичное
отклонение s*=
и среднеквадратичное
отклонение s*=![]() .
.
- Дисперсия
Для каждого «куска» ряда вычисляется дисперсия ![]() (
(![]() ;
; ![]() ). Затем считаем среднее от
). Затем считаем среднее от
![]() и среднеквадратичное
отклонение s*=
и среднеквадратичное
отклонение s*=![]() .
.
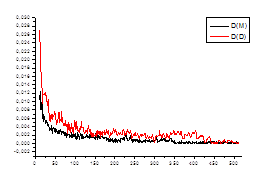
Рис. 2.3. Зависимости среднеквадратичного отклонения D(M) и D(D) от ![]() .
.
В нашем случае, критерием стационарности является минимум
среднеквадратичного отклонения от значения автокорреляционной функции, минимум ![]() и
и ![]() .
.
Этому условию удовлетворяет «кусок» ряда, длиной ![]() .
.
Таким образом, исходный ряд стационарен на периоде T=21 год.
1. Оценка математического ожидания
Проверяем
Ø состоятельность оценки для каждого стационарного «куска» ряда.
![]() ,
,
где ![]() – математическое
ожидание на стационарном периоде
– математическое
ожидание на стационарном периоде
![]() – среднее значение в зависимости от числа данных
– среднее значение в зависимости от числа данных
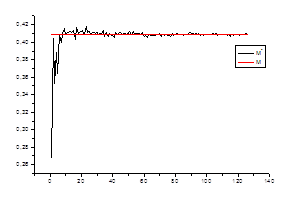
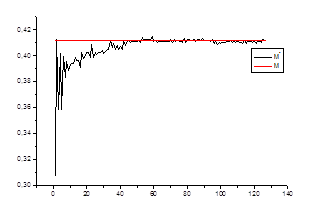
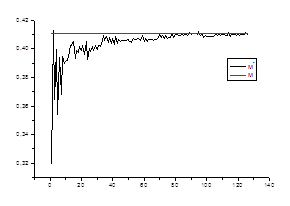
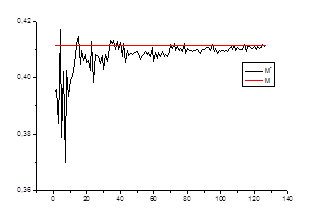
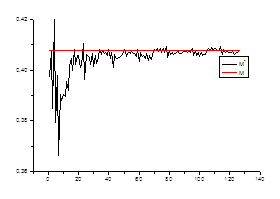
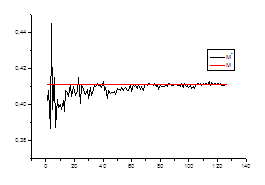
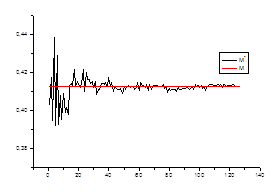
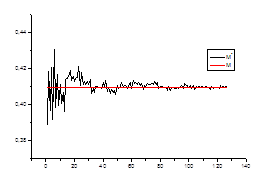
Ø несмещенность оценки
M [a*] = a,
|
Номер интервала |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
M [a*] |
0,40938 | 0,41218 | 0,41058 | 0,41152 | 0,40758 | 0,41118 | 0,41259 | 0,40985 |
|
a |
0,40714 | 0,40661 | 0,40437 | 0,4080 | 0,40492 | 0,40906 | 0,41206 | 0,41018 |
2. Оценка дисперсии
Проверяем
Ø состоятельность оценки для каждого стационарного «куска» ряда.
![]() ,
,
где ![]() – среднеквадратичное
отклонение на стационарном периоде
– среднеквадратичное
отклонение на стационарном периоде
![]() - среднеквадратичное отклонение в
зависимости от числа данных
- среднеквадратичное отклонение в
зависимости от числа данных
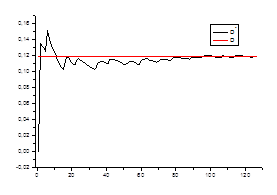
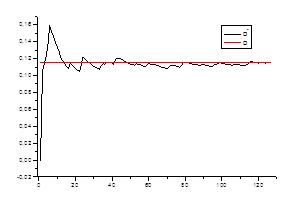
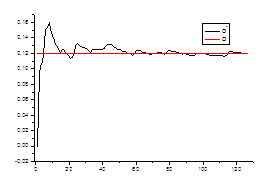
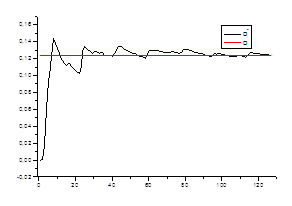
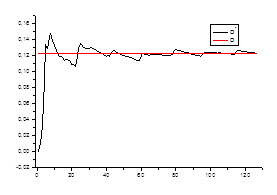

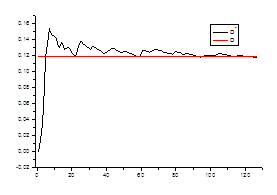
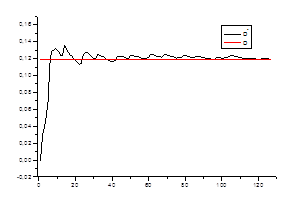
Ø несмещенность оценки
M [a*] = a,
|
Номер интервала |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
M [a*] |
0,11862 | 0,11507 | 0,11944 | 0,1235 | 0,12227 | 0,11891 | 0,11709 | 0,1185 |
|
a |
0,11477 | 0,11391 | 0,12122 | 0,11959 | 0,11959 | 0,11674 | 0,12163 | 0,11842 |
3. Вычислить куммулятивную частоту превышения уровня и сделать оценки ее стационарности
![]() – куммулятивная частота превышения уровня
а.
– куммулятивная частота превышения уровня
а.

Рис. 3.1. Зависимость куммулятивной частоты от уровня превышения.
Разбиваем исходный ряд на на ![]() отрезков,
для каждого «куска» ряда строим функции зависимости куммулятивной частоты от
уровня превышения, и оцениваем стационарность полученных
отрезков,
для каждого «куска» ряда строим функции зависимости куммулятивной частоты от
уровня превышения, и оцениваем стационарность полученных
n-зависимостей критериям, полученным в п. 2.
Анализируя оценки корреляционной функции, математического ожидания и дисперсии, находим период стационарности куммулятивной частоты превышения уровня T=17.85 лет.
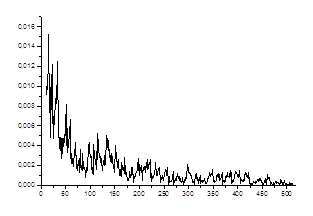
Рис. 3.2. Оценка корреляционной функции
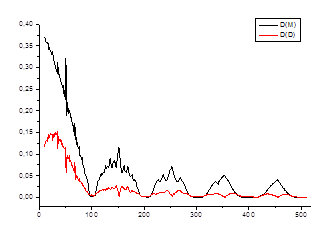
Рис. 3.3. Оценки математического ожидания и дисперсии.
4. С помощью пуассоновской статистики дать долгосрочный прогноз превышения уровня. На какой срок Вы гарантируете такой прогноз?
![]()
– искомая формула вероятности того, что за период
времени T произойдет ровно m превышений уровня a. Вероятность
возникновения таких ситуаций определяется средней частотой превышения уровня a и временем прогноза. Из
анализа данных за 176 лет на стационарном периоде находим функцию зависимости средней
частоты от уровня a ![]() .
.
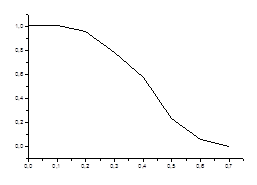
Рис. 4.1. Средняя частота превышения уровня
Нас интересуют редкие события, например, превышение уровня ![]() . Соответственно, среднюю
частоту превышения такого уровня можно определить из графика
. Соответственно, среднюю
частоту превышения такого уровня можно определить из графика ![]() , и она равна
, и она равна
![]() 0.0635
0.0635
Зная среднюю частоту, теперь можно вычислить вероятность того, что за период, например, равный 220 лет, произойдет ровно 1,2,3,4.
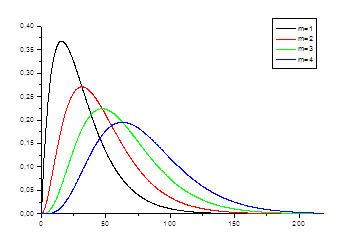
Рис. 4.2. Вероятность возникновения ровно m – аварий
Зависимости вероятности от прогнозируемого времени для
разного числа превышения уровня (m=1,2,3,4) являются немонотонными, и их максимум
приходится на моменты времени ![]()
Как видно из графика, сначала более вероятным является только одно превышение уровня a=0.6, затем два, три…
Например, вероятность того, что за 62 года произойдет три превышения уровня a=0.6, самая высокая и равна p= 0,19775.
5. Рассчитайте среднюю частоту появления выбросов и среднее время выброса
Будем рассматривать выбросы (превышение уровня, например, a=0.6) за период, на котором исходный ряд стационарен.
Выброс характеризуется следующим условием
![]()
Тогда можем найти среднюю частоту выброса за уровень а=0.6
![]() =0.063
=0.063
Средняя продолжительность выброса для стационарных случайных процессов
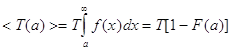
Отсюда, зная функцию распределения случайной величины, порог, начиная с которого процесс ведет к катастрофе, и период прогноза, можно рассчитать среднее время катастрофической ситуации, в нашем случае – превышение заданного уровня.
Среднее число выбросов за период T для стационарного процесса определяется:
![]()
где P – среднюю частоту выброса
Таким образом, среднее число катастроф пропорционально продолжительности времени прогноза и падает с увеличением порогового значения, определяющего возникновение катастрофической ситуации.
Средняя продолжительность выброса может быть вычислена по формуле
![]()
и она не зависит от прогнозируемого времени (для стационарных процессов
Средняя продолжительность выброса за уровень а=0.6
равна ![]() лет.
лет.
6. Попытайтесь сделать краткосрочный прогноз уровня воды, используя линейный и корреляционный анализ. Проверьте его на уже имеющихся данных
1. Линейный прогноз.
Рассматриваем наш ряд на стационарном периоде T. Выбираем n=127 точек. Тогда
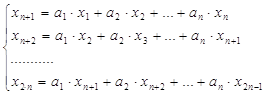
Нам известны значения ![]() .
Решая систему уравнений, находим коэффициенты
.
Решая систему уравнений, находим коэффициенты ![]() .
.
Тогда можем спрогнозировать любую точку ряда, например, ![]() :
:
![]()
В качестве проверки найденных коэффициентов сделали прогноз с 22-ого по 33-ий год (рис. 6.1) и c 33-ого по 44-ий год (рис. 6.2).
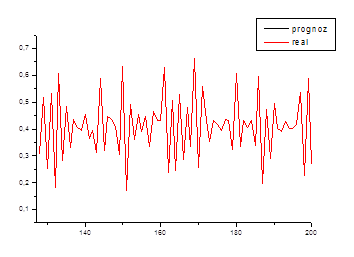
Рис. 6.1. Линейный прогноз с 22-ого по 33-ий год
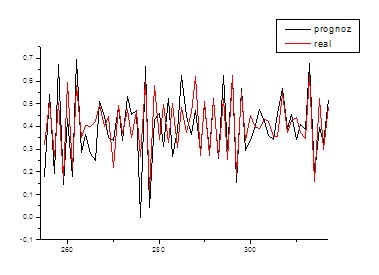
Рис. 6.2. Линейный прогноз с 33-ого по 44-ый год
2. Корреляционный прогноз
Рассматриваем наш ряд на стационарном периоде T. Тогда можем представить в виде
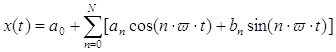
где
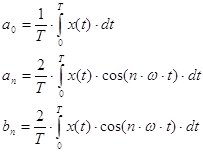
Зная коэффициенты ![]() и
и ![]() можно спрогнозировать
уровень воды, например, на 33 года.
можно спрогнозировать
уровень воды, например, на 33 года.
В качестве проверки найденных коэффициентов сделали прогноз на первые 22 года (рис. 6.3) и с 22-ого по 33-ий год (рис. 6.4). Как видно из графиков. Результаты совпадают в пределах погрешности.
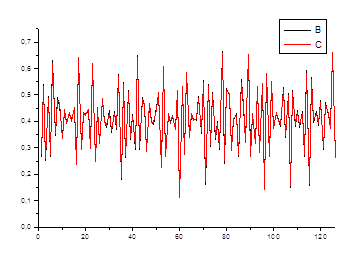
Рис. 6.3. Корреляционный прогноз на первые 22 года
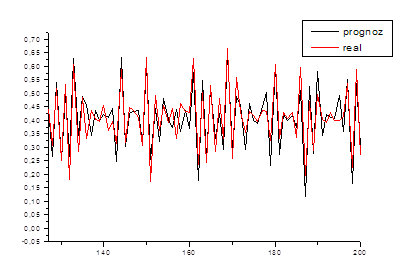
Рис. 6.4. Корреляционный прогноз с 22-ого по 33-ий год
Анализируя полученные результаты и используя уже известные данные, можно сказать, что корреляционный прогноз более точный.