Контрольная работа: Математические уравнения и функции
Варивант №2
Задание 1
Дан треугольник ABC, где А(-3,2), В(3,-1), С(0,3). Найти:
1. Длину стороны АВ;
2. Внутренний угол А с точностью до градуса;
3. Уравнение и длину высоты, опущенной из вершины С;
4. Точку пересечения высот;
5. Уравнение медианы, опущенной из вершины С;
6. Систему неравенств, определяющих треугольник АВС;
7. Сделать чертеж;
Решение:
1. Найдем координаты вектора АВ:
![]()
Длина стороны АВ равна:
![]()
2. Угол А будем искать как угол между векторами АВ и АС(-3,1)
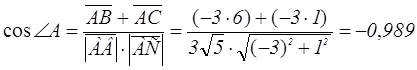
Тогда ![]()
3.
Прямая
СК перпендикулярна АВ проходит через точку С(0,3) и имеет нормалью вектор ![]() .
.
По формуле получим уравнение высоты:
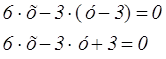
Сокращаем на 3 получим уравнение высоты:
![]()
4. Координаты основания медианы будут:
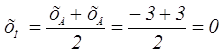 ;
;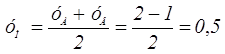
Уравнение медианы найдем, пользуясь данной формулой, как уранение прямой, проходящей через 2 точки: С и М
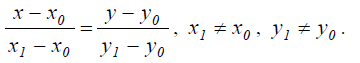
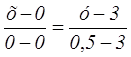
Так как знаменатель левой части равен нулю, то уравнение медианы будет иметь такой вид х=0
5.
Известно
что высоты треугольника пересекаются в одной точке Р. Уравнение высоты СК
найдено, выведем аналогично высоту BD
проходящую через точку В перпендикулярно вектору ![]()
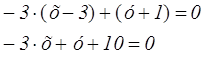
Координаты точки Р найдем как решение системы уравнений:
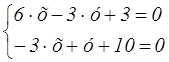
х=11 у=23
6.
Длину
высоты hc будем ее искать как
расстояние от точки С до прямой АВ. Эта прямая проходит через точку А и имеет
направляющий вектор ![]() .
.
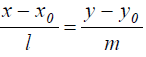
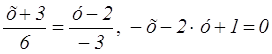
Теперь воспользовавшись формулой
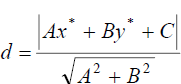
Подставляя в нее координаты точки С(0,3)
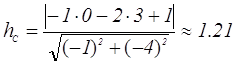
Задание 2
Даны векторы ![]() Доказать, что
Доказать, что ![]() образуют базис
четырехмерного пространства, и найти координаты вектора «в» в этом базисе.
образуют базис
четырехмерного пространства, и найти координаты вектора «в» в этом базисе.
![]()
Решение:
1.
Докажем,
что подсистема ![]() линейно
независима:
линейно
независима:
![]()
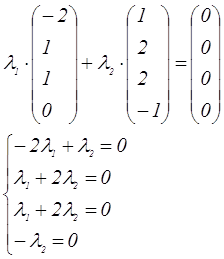
Из четвертого уравнения имеем , что
![]() , тогда из
первого, второго и третьего следует, что
, тогда из
первого, второго и третьего следует, что ![]() .
Линейная независимость доказана.
.
Линейная независимость доказана.
Докажем, что векторы ![]() можно представить в виде
линейных комбинации векторов
можно представить в виде
линейных комбинации векторов ![]() .
.
Очевидно,
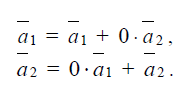
Найдем представление ![]() через
через ![]() .
.
![]()
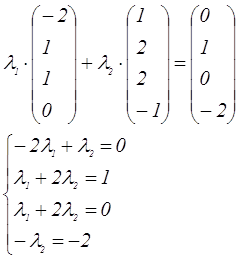
Из четвертого уравнения находим ![]() и подставляем в первые три
и подставляем в первые три
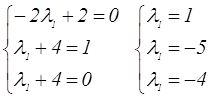
Получили , что данная система векторов не может называться базисом!
Задание 3
Найти производные функций:

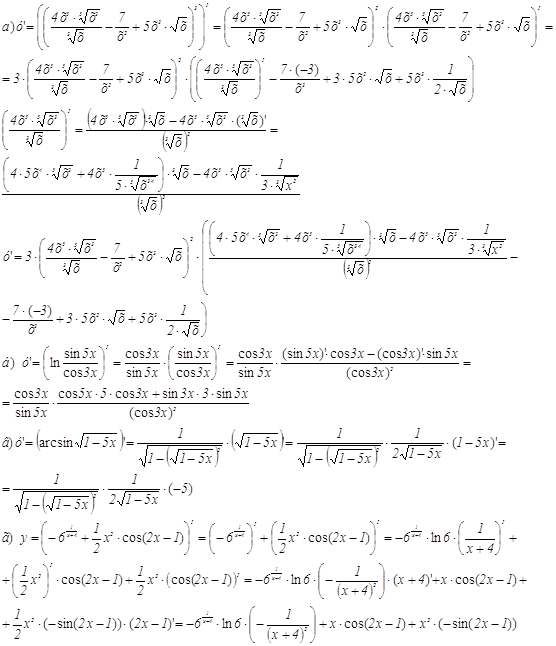
Задание 4.
Исследовать функцию и построить ее график
![]()
1. Область определения:
![]() ,
то есть
,
то есть ![]()
2. Кривая
![]() имеет вертикальную
ассимптоту х=-1, так как
имеет вертикальную
ассимптоту х=-1, так как
![]()
Находим наклонные асимптоты. ![]() а то означает, что есть
вертикальная асимптота у=0.
а то означает, что есть
вертикальная асимптота у=0.
3.
Функция
общего вида, так как ![]() и
и ![]()
4. Функция периодичностью не обладает
5. Находим производную функции
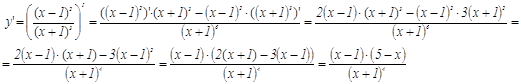
Получаем 3 критические точки х=-1 х=1, и х=5.
Результаты исследования на монотонность и экстремумы оформляется в виде таблицы
| х |
|
|
1 |
|
5 |
|
| y’ | - | - | 0 | + | 0 | - |
| y | убывает | убывыает |
0 min |
возрастает | 0,074 | убывает |
6. Находим вторую производную функции
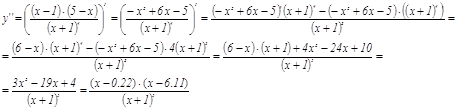
Получаем критические точки х=-1; х=0,22; х=6,11
Результаты исследований на выпуклость и точки перегиба оформляем в виде таблицы.
| х |
|
|
0.22 |
|
6.11 |
|
| y” | - | + | 0 | + | 0 | - |
| y | выпукла | вогнута |
0,335 перегиб |
вогнута | 0,072 | выпукла |
7. Находим точки пересечения графика с осями координат Ох и Оу
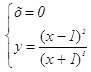 получаем
точку (0;1);
получаем
точку (0;1); 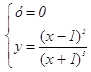 получаем
точку (1;0)
получаем
точку (1;0)
8. При х=-2, у=-9, при х=-5, у=-0,56, при х=-10, у=-0,166
9. Строим график в соответствии с результатами исследований:
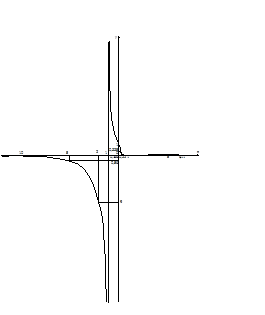
Задание 5
Найти неопределенные интегралы и проверить их дифференцированием.
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]()
Решение:
а) сделаем подстановку sin3x=t, тогда dt=cos3x dx, следовательно:
![]()
Проверка:
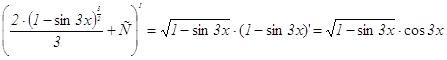
б) сделаем подстановку ![]()
![]()
Проверка:
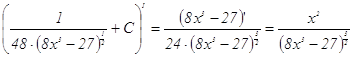
в) Воспользуемся способом интегрирования по частям
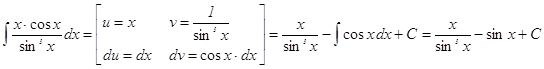
Проверка:
![]()
г) воспользуемся способом интегрирования рациональных дробей
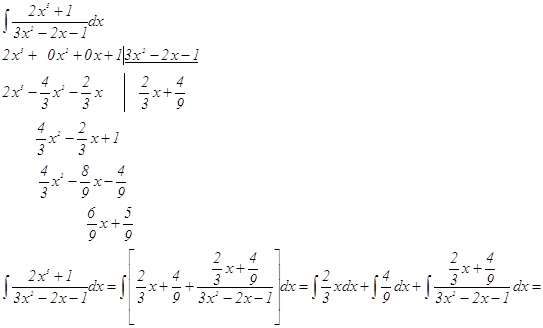
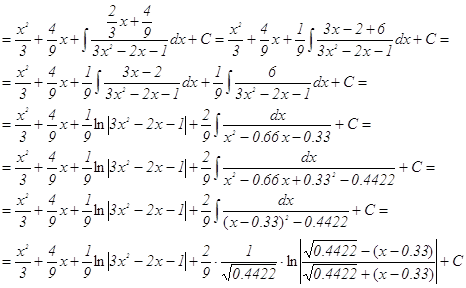
Проверка:
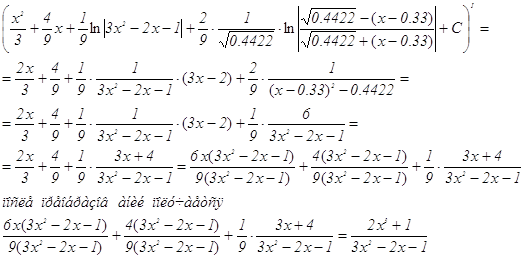
Задание 6
Вычислить площадь фигуры, ограниченной графиками функций:
![]()
Решение:
находим координаты точек пересечения заданных графиков функций:
![]() приравнивая правые части, получаем квадратное
уравнение
приравнивая правые части, получаем квадратное
уравнение
![]() корни
этого квадратного уравнения
корни
этого квадратного уравнения ![]()
следовательно : ![]() ,
и значит координаты точек пересечения А(0,7) и В(5,2). Точка х=2 находится
между точками 0 и 5. Подставляя в уравнения 2 получаем:
,
и значит координаты точек пересечения А(0,7) и В(5,2). Точка х=2 находится
между точками 0 и 5. Подставляя в уравнения 2 получаем: ![]()
т.к![]() получаем:
получаем:
![]()
![]()
![]()
![]()
0,335
перегиб
7. Находим точки пересечения графика с осями координат Ох и Оу
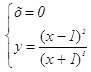 получаем
точку (0;1);
получаем
точку (0;1); 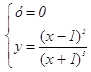 получаем
точку (1;0)
получаем
точку (1;0)
8. При х=-2, у=-9, при х=-5, у=-0,56, при х=-10, у=-0,166
9. Строим график в соответствии с результатами исследований:
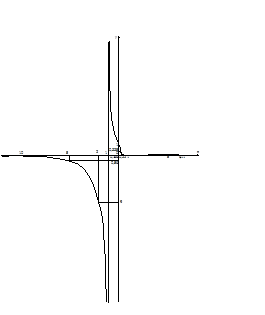
Задание 5
Найти неопределенные интегралы и проверить их дифференцированием.
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]()
Решение:
а) сделаем подстановку sin3x=t, тогда dt=cos3x dx, следовательно:
![]()
Проверка:
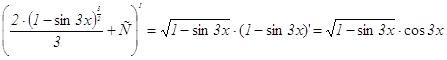
б) сделаем подстановку ![]()
![]()
Проверка:
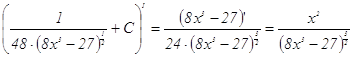
в) Воспользуемся способом интегрирования по частям
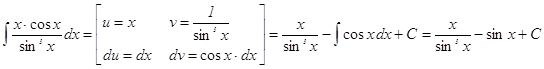
Проверка:
![]()
г) воспользуемся способом интегрирования рациональных дробей
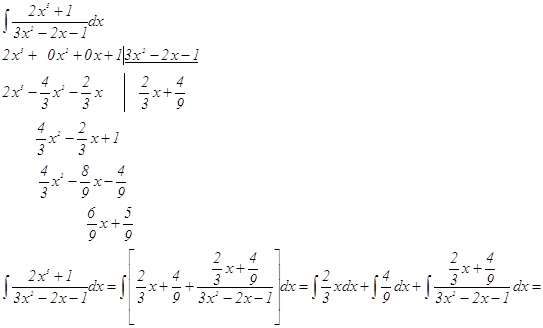
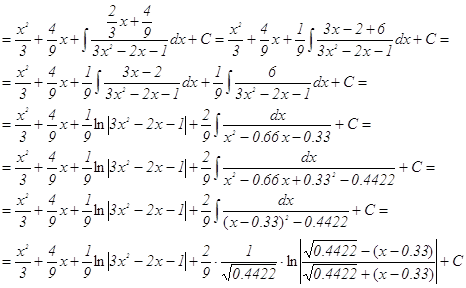
Проверка:
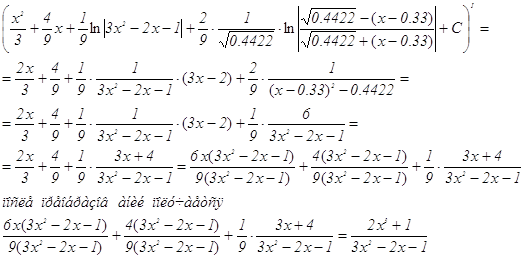
Задание 6
Вычислить площадь фигуры, ограниченной графиками функций:
![]()
Решение:
находим координаты точек пересечения заданных графиков функций:
![]() приравнивая правые части, получаем квадратное
уравнение
приравнивая правые части, получаем квадратное
уравнение
![]() корни
этого квадратного уравнения
корни
этого квадратного уравнения ![]()
следовательно : ![]() ,
и значит координаты точек пересечения А(0,7) и В(5,2). Точка х=2 находится
между точками 0 и 5. Подставляя в уравнения 2 получаем:
,
и значит координаты точек пересечения А(0,7) и В(5,2). Точка х=2 находится
между точками 0 и 5. Подставляя в уравнения 2 получаем: ![]()
т.к![]() получаем:
получаем:
![]()