Курсовая работа: Метод комплексных чисел в планиметрии

    В данной работе рассмотрен метод комплексных чисел в планиметрии, применение его критериев в задачах элементарного характера на темы – «Параллельность, коллинеарность, перпендикулярность», «Углы и площади», «Многоугольники», «Прямая и окружность».

    Метод комплексных чисел в иностранной литературе используется достаточно широко. Однако в отечественной литературе этот метод не получил широкого распространения. Имеются отдельные фрагменты в книге З. А. Скопеца. Систематическое изложение этого метода дано в книге Я. П. Понарина «Алгебра комплексных чисел в геометрических задачах». Нами выбраны и решены на наш взгляд наиболее интересные задачи, выполняемые этим методом.

    Метод комплексных чисел позволяет решать планиметрические задачи прямым вычислением по готовым формулам. Выбор этих формул с очевидностью диктуется условием задачи и её требованием. В этом состоит необычайная простота этого метода по сравнению с векторным и координатным методами, методом геометрических преобразований, конструктивно-синтетическим методом, требующими от решающего порой немалой сообразительности и длительных поисков, хотя при этом готовое решение может быть коротким.

§ 1 Параллельность, коллинеарность, перпендикулярность.

    1.1. Коллинеарность векторов .

                                                                         (1.2)

    1.2. Коллинеарность трёх точек .

                                                                                            (1.3)

Это – критерий принадлежности точек А, В, С одной прямой.

                                                                                                   (1.5)

определяет прямую, содержащую хорду АВ единичной окружности.

    1.3. Перпендикулярность отрезков (векторов) .

                                                        (1.7)

Уравнение касательной

                                                                                                   (1.8)

                                                                                                       (1.9)

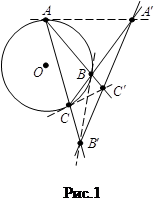
    З а д а ч а 1. Доказать, что точки пересечения прямых, содержащих стороны треугольника, с касательными к описанной окружности в противоположных им вершинах коллинеарны.

§ 2 Углы и площади

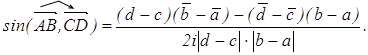
    2.1. Угол между векторами.

(2.1)

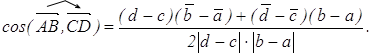
(2.2)

    2.2. Площадь треугольника

                                  (2.3)

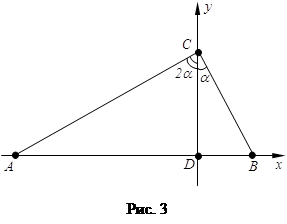
    З а д а ч а 2. Основание D высоты CD треугольника ABC делит сторону AB в отношении 3:1. Угол ACD вдвое больше угла BCD. Вычислить углы треугольника ABC.

    3.1. Подобные треугольники.

                                          (3.1)

где  – комплексное число,  – коэффициент подобия.

                                          (3.2)

где  – комплексное число,  – коэффициент подобия.

    Если , то треугольники  и  равны. Тогда соотношение (3.1) – признак равенства одинаково ориентированных треугольников, а соотношение (3.2) – признак равенства противоположно ориентированных треугольников.

    3.2. Критерий правильного треугольника .

Треугольник ориентирован положительно:                               

                                                                                                  (3.4)

Треугольник ориентирован отрицательно:                                

                                                  (3.5)

3.3  Правильные многоугольники.

где k принимает значения . Все n значений имеют один и тот же модуль  

Корням уравнения

соответствуют вершины .

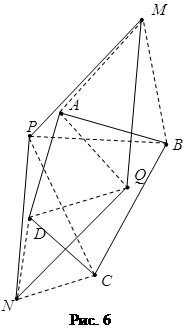    З а д а ч а 3. Точки  симметричны точке Р, лежащей в плоскости треугольника ABC, относительно, соответственно, прямых AB, BC, CA. Точки  – середины отрезков  Докажите, что треугольники  и  подобны и противоположно ориентированы (рис. 5).

    З а д а ч а 4. На сторонах  и  выпуклого четырёхугольника  вне его построены правильные треугольники  и  а на сторонах  и  построены правильные треугольники  и  лежащие с четырёхугольником в одной полуплоскости относительно прямых  и  соответственно. Докажите, что  –параллелограмм (рис. 6).

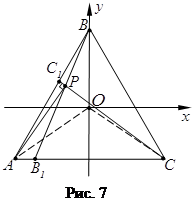
    З а д а ч а 5. Точка  делит сторону  правильного треугольника  в отношении 3:2 считая от точки . Точка  делит сторону  в отношении 3:14, считая от точки . Отрезки  и  пересекаются в точке. Докажите, что прямые  и  перпендикулярны.

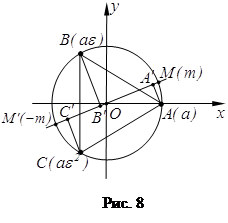
    З а д а ч а 6. Через центр правильного треугольника проведена прямая. Доказать, что сумма квадратов расстояний от вершин  треугольника до прямой не зависит от выбора прямой.

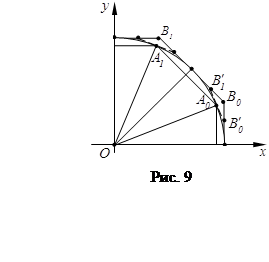
    З а д а ч а 7. Пусть d – диаметр окружности,  и

 – стороны вписанного в неё и описанного около

неё правильных n-угольников.  Докажите, что

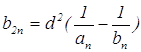 (рис. 9).

    4.1. Уравнение прямой .

                                                    (4.1)

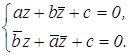
Пусть коэффициенты a и b не обращаются в нуль одновременно. Приходим к уравнению:  которое а) имеет единственное решение при  б) имеет бесконечное множество решений при

    Отсюда и на основании предыдущих исследований получаем, что уравнение (4.1) определяет а) единственную точку при  б) прямую при  в) пустое множество при

    4.3. Общее уравнение окружности в сопряжённых комлексных координатах . Окружность с центром S(s) и радиусом R имеет уравнение

                                                                                            (4.2)

где z – координата переменной точки окружности.

                                                (4.4)

Сравнивая уравнение (4.3) с уравнением (4.2) приходим к выводу, что уравнения (4.3) и (4.2) задают окружность тогда и только тогда, когда  и ab - c – действительное число. Отсюда , а значит, с должно быть действительным числом. Итак, уравнение

                                               (4.5)

есть уравнение окружности с центром  и радиусом

    4.4. Уравнение окружности по трём данным точкам . Пусть окружность  проходит через точки A, B, C. Тогда однородная линейная система

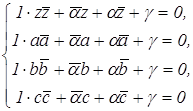
относительно  имеет ненулевое решение (так как окружности определяются тремя неколлинеарными точками), поэтому её определитель равен нулю:

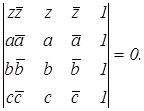                                              (4.6)

Это уравнение представляет собой уравнение окружности по трём данным точкам.

    4.5. Ортогональные окружности. Две пересекающиеся окружности называются ортогональными, если касательные к ним в их общей точке перпендикулярны. Очевидно, что касательная к одной из окружностей в их общей точке содержит центр другой окружности.

    Даны две окружности (A,R) и (B,r), заданные соответственно уравнениями:  где  и  где  Для того, чтобы эти окружности были ортогональны, необходимо и достаточно, чтобы  или

                                             (4.7)

или

                                                      (4.8)

    З а д а ч а 7. В плоскости даны два отрезка AB и CD. Найдите множество точек М, для каждой из которых площади треугольников MAB и MDC равны (рис. 10).

З а д а ч а 9.  На гипотенузе AB прямоугольного треугольника  ABC дана произвольная точка P. Докажите, что окружности, описанные около треугольников  APC  и BPC, ортогональны.

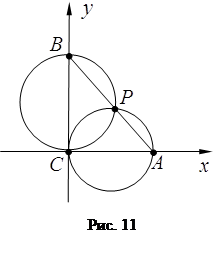Д о к а з а т е л ь с т в о. Примем вершину С  данного треугольника за начальную точку. Пусть точкам А, В, P соответствуют комплексные числа 1, b, p, а центрам окружностей РАС и РВС числа  (рис. 11). По условию  или . Переходя к комплексным числам, получаем:  откуда .

    Руководствуясь (4.6), составим уравнение окружности РВС:

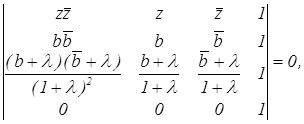
или

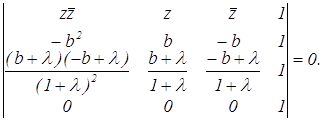
После раскрытия определителя получаем:

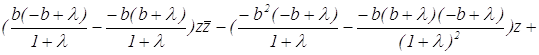
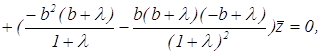
или

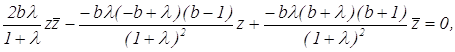
откуда

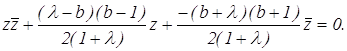
    Из уравнения находим: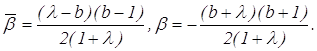

Аналогично, для окружности РAС имеем:

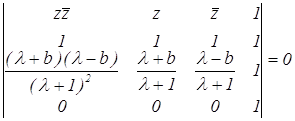
и

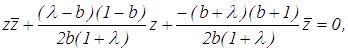
отсюда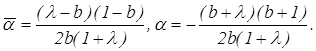

Согласно критерию (4.8) для того, чтобы окружности РАС и РВС были ортогональны необходимо и достаточно, чтобы  Учитывая предыдущие результаты, проверим выполнимость данного критерия:

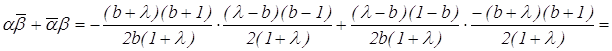
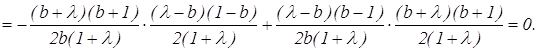
    Таким образом, окружности РАС и РВС являются ортогональными.