Реферат: Регрессионный анализ. Парная регрессия

РЕФЕРАТ

Регрессионный анализ. Парная регрессия.

I. Построение регрессионных моделей

1. Смысл регрессионного анализа – построение функциональных зависимостей между двумя группами переменных величин Х₁, Х₂, … Х_р и Y. При этом речь идет о влиянии переменных Х (это будут аргументы функций) на значения переменной Y (значение функции). Переменные Х мы будем называть факторами, а Y – откликом.

Сегодня мы разберем наиболее простой случай – установление зависимости одного отклика y от одного фактора х. Такой случай называется парной (простой) регрессией.

2. Построение модели

Этап 1. Исходные данные: заранее известные (экспериментальные, наблюденные) значения фактора х_i – экзогенная переменная и соответствующие им значения отклика y_i, (i = 1,…,n) - эндогенная переменная;

Активный и пассивный эксперимент.

Выборочные характеристики – позволяют кратко охарактеризовать выборку, т. е., получить ее модель, хотя и очень грубую:

а) среднее арифметическое:

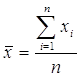
Среднее арифметическое – это «центр», вокруг которого колеблются значения случайной величины.

Пример: средняя продолжительность жизни в России и США

б) дисперсия:

Отклонение от среднего: - характеризует лишь «разброс» конкретной, отдельно взятой величины х_i. Если мы захотим получить более полную информацию, нам придется выписать такие отклонения для всех х, т. е., получить такой же ряд чисел, как и исходная выборка.

Можно попытаться усреднить все отклонения, но «среднее арифметическое отклонений от среднего арифметического» имеет особенность:

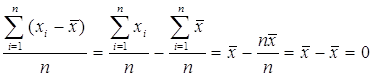
Эта величина обнуляется из-за того, что отрицательные значения отклонений и положительные взаимно погашаются.

Чтобы избежать этого, возведем их в квадрат, получив так называемую выборочную дисперсию:

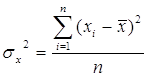
Выборочная дисперсия характеризует разброс (вариацию) элементов выборки вокруг их среднего арифметического. Важно иметь в виду, что сами элементы выборки и их дисперсия имеют разные порядок: если элементы выборки измеряются в метрах, то дисперсия – в квадратных метрах.

Стандартное отклонение:

Полезное свойство дисперсии:

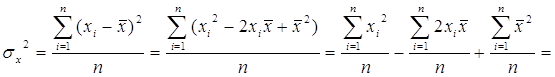
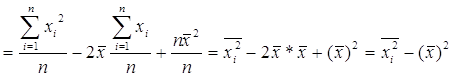
Т. о.

Характеристики генеральной совокупности:

математическое ожидание М(Х)

дисперсия D(X)

Несмещенная оценка дисперсии:

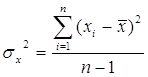
Для простоты, мы будем использовать смещенную оценку – выборочную дисперсию – при достаточно больших n они практически равны.

Этап 2. Постановка задачи: предположим, что значение каждого отклика y_i как бы состоит из двух частей:

- во-первых, закономерный результат того, что фактор х принял конкретное значение х_i;

- во-вторых, некоторая случайная компонента e_i, которая никак не зависит от значения х_i.

Таким образом, для любого i = 1,…,n

y_i = f(x_i) + e_i

Смысл случайной величины (ошибки) e:

а) внутренне присущая отклику у изменчивость;

б) влияние прочих, не учитываемых в модели факторов;

в) ошибка в измерениях

Этап 3. Предположения о характере регрессионной функции

Возможный вид функции f(x_i)

- линейная:

- полиномиальная

- степенная:

- экспоненциальная:

- логистическая:

Методы подбора вида функции:

- графический

- аналитический

Этап 4. Оценка параметров линейной регрессионной модели

1. Имея два набора значений: x₁, x₂, …, x_n и y₁, y₂, …, y_n, предполагаем, что между ними существует взаимосвязь вида:

y_i = a + bx_i + e_i

т. н. функция регрессии

Истинные значения параметров функции регрессии мы не знаем, и узнать не можем.

Задача: построить линейную функцию:

ŷ_i = a + bx_i

так, чтобы вычисленные значения ŷ_i(x_i) были максимально близки к экспериментальным у_i (иначе говоря, чтобы остатки (ŷ_i - y_i) были минимальны).

Экономическая интерпретация коэффициентов:

a – «постоянная составляющая» отклика, независимая от фактора

b – степень влияния фактора на отклик (случаи отрицательного)

2. Метод наименьших квадратов (МНК):

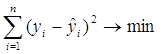
подставим в задачу формулу (2.2):

В данном случае у нас a и b – переменные, а х и у – параметры. Для нахождения экстремума функции, возьмем частные производные по a и b и приравняем их к нулю.

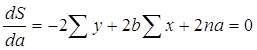
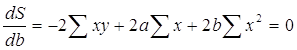
Получили систему из двух линейных уравнений. Разделим оба на 2n:

Из первого уравнения выразим неизвестную а:

и подставим это выражение во второе уравнение:

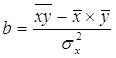
Построив оценки a и b коэффициентов a и b, мы можем рассчитать т. н. «предсказанные», или «смоделированные» значения ŷ_i = a + bx_i и их вероятностные характеристики – среднее арифметическое и дисперсию.

Несложно заметить, что оказалось. Так должно быть всегда:

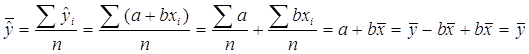
Кроме того, вычислим т. н. случайные остатки и рассчитаем их вероятностные характеристики.

Оказалось, . Это также закономерно:

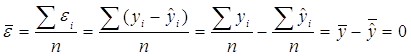
Таким образом, дисперсия случайных остатков будет равна:

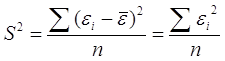
Мы произвели вычисления, и построили регрессионное уравнение, позволяющее нам построить некую оценку переменной у (эту оценку мы обозначили ŷ). Однако, если бы мы взяли другие данные, по другим областям (или за другой период времени), то исходные, экспериментальные значения х и у у нас были бы другими и, соответственно, а и b, скорее всего, получились бы иными.

Вопрос: насколько хороши оценки, полученные МНК, иначе говоря, насколько они близки к «истинным» значениям a и b?

Этап 5. Исследование регрессионной модели

1. Теснота связи между фактором и откликом

Мерой тесноты связи служит линейный коэффициент корреляции:

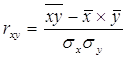                      (2.13)

-1 £ r_xy £ 1                              (2.14)

Отрицательное значение КК означает, что увеличение фактора приводит к уменьшению отклика и наоборот:

2. Доля вариации отклика у, объясненная полученным уравнением регрессии характеризуется коэффициентом детерминации R². Путем математических преобразований можно выразить:

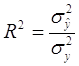
где – оценка дисперсии случайных остатков в модели,

Таким образом, R² – это доля дисперсии у, объясненной с помощью регрессионного уравнения в дисперсии фактически наблюденного у.

Очевидно:

0 £ R² £ 1

3. Проверка статистической значимости уравнения регрессии

Мы получили МНК-оценки коэффициентов уравнения регрессии и рассчитали коэффициент детерминации. Однако, осталось неясным, достаточно ли он велик, чтобы говорить о существовании значимой связи между величинами х и у. Иначе говоря, достаточно ли сильна эта связь, чтобы на основании построенной нами модели можно было бы делать выводы?

Для ответа на этот вопрос можно провести т. н. F-тест.

Формулируется гипотеза Н₀: предположим, что y_i ¹ a + bx_i + e_i

Обратить внимание: выписаны не а, а a, т. е., не оценки коэффициентов регрессии, а их истинные значения.

Альтернатива – гипотеза Н₁: y_i = a + bx_i + e_i

Мы не можем однозначно подтвердить или опровергнуть гипотезу Н₀, мы можем лишь принять или отвергнуть ее с определенной вероятностью.

Выберем некоторый уровень значимости g, такой что 0 £ g £ 1 – вероятность того, что мы сделаем неправильный вывод, приняв или отклонив гипотезу Н₀.

Соответственно, величина Р = 1 - g - доверительная вероятность – вероятность того, что мы в итоге сделаем правильный вывод.

Для проверки истинности гипотезы Н₀, с заданным уровнем значимости g, рассчитывается F-статистика:

Значение F-статистики в случае парной регресии подчиняется т. н.

F-распределению Фишера с 1 степенью свободы числителя и (n - 2) степенями свободы знаменателя.

Для проверки Н₀ величина F-статистики сравнивается с табличным значением F_g(1, n-2).

Если F > F_g(1, n-2) – гипотеза Н₀ отвергается, т. е. мы считаем, что с вероятностью 1-g можно утверждать, что регрессия имеет место и:

y_i = a + bx_i + e_i

В противном случае гипотеза Н₀ не отвергается, принимаем:

y_i ¹ a + bx_i + e_i

Вопрос: почему бы нам не взять g поменьше? Чем меньше g, тем больше соответствующее табличное значение F-статистики, т. е., тем меньше шансов, что появятся основания отвергнуть гипотезу Н₀.

Ошибки первого и второго рода

Ошибка первого рода: отвергается Н₀, которая на самом деле верна.

Ошибка второго рода: принимается H0, которая на самом деле не верна.

Очевидно, чем меньше g, тем меньше наши шансы отвергнуть гипотезу Н₀, т. е., совершить ошибку первого рода. Соответственно, шансы совершить ошибку второго рода увеличиваются.

4. Характеристика оценок коэффициентов уравнения регрессии

1) математическое ожидание

Теорема: М(а) = a, M(b) = b - несмещенность оценок

Это означает, что при увеличении количества наблюдений значения МНК-оценок a и b будут приближаться к истинным значениям a и b;

2) дисперсия

Теорема:

;  

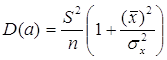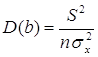
Благодаря этой теореме, мы можем получить представление о том, как далеко, в среднем, наши оценки a и b находятся от истинных значений a и b.

Необходимо иметь в виду, что дисперсии характеризуют не отклонения, а «отклонения в квадрате». Чтобы перейти к сопоставимым значениям, рассчитаем стандартные отклонения a и b:

;     

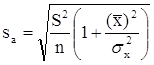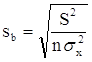
Будем называть эти величины стандартными ошибками a и b соответственно.

5. Построение доверительных интервалов

Пусть мы имеем оценку а. Реальное значение коэффициента уравнения регрессии a лежит где-то рядом, но где точно, мы узнать не можем. Однако, мы можем построить интервал, в который это реальное значение попадет с некоторой вероятностью. Доказано, что:

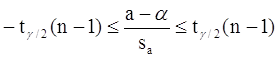
с вероятностью Р = 1 - g

где t_g/2(n-1) - g/2-процентная точка распределения Стьюдента с (n-1) степенями свободы – определяется из специальных таблиц.

При этом уровень значимостиg устанавливается произвольно.

Неравенство можно преобразовать следующим образом:

,

или, что то же самое:

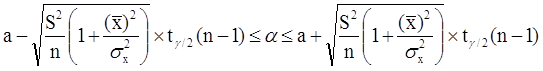
Аналогично, с вероятностью Р = 1 - g:

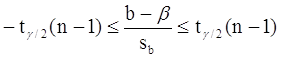
откуда следует:

,

или:

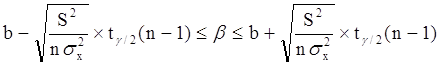
Уровень значимости g - это вероятность того, что на самом деле истинные значения a и b лежат за пределами построенных доверительных интервалов. Чем меньше его значение, тем больше величина t_g/2(n-1), соответственно, тем шире будет доверительный интервал.

6. Проверка статистической значимости коэффициентов регрессии

Мы получили МНК-оценки коэффициентов, рассчитали для них доверительные интервалы. Однако мы не можем судить, не слишком ли широки эти интервалы, можно ли вообще говорить о значимости коэффициентов регрессии.

Гипотеза Н₀: предположим, что a=0, т. е. на самом деле независимой постоянной составляющей в отклике нет (альтернатива – гипотеза Н₁: a ¹ 0).

Для проверки этой гипотезы, с заданным уровнем значимости g, рассчитывается t-статистика, для парной регрессии:

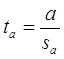
Значение t-статистики сравнивается с табличным значением t_g/2(n-1) - g/2-процентной точка распределения Стьюдента с (n-1) степенями свободы.

Если |t| < t_g/2(n-1) – гипотеза Н₀ не отвергается (обратить внимание: не «верна», а «не отвергается»), т. е. мы считаем, что с вероятностью 1-g можно утверждать, что a = 0.

В противном случае гипотеза Н₀ отвергается, принимается гипотеза Н₁.

Аналогично для коэффициента b формулируем гипотезу Н₀: b = 0, т. е. переменная, выбранная нами в качестве фактора, на самом деле никакого влияния на отклик не оказывае.

Для проверки этой гипотезы, с заданным уровнем значимости g, рассчитывается t-статистика:

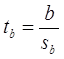
и сравнивается с табличным значением t_g/2(n-1).

Если |t| < t_g/2(n-1) – гипотеза Н₀ не отвергается, т. е. мы считаем, что с вероятностью 1-g можно утверждать, что b = 0.

В противном случае гипотеза Н₀ отвергается, принимается гипотеза Н₁.

7. Автокорреляция остатков.

1. Примеры автокорреляции.

Возможные причины:

1) неверно выбрана функция регрессии;

2) имеется неучтенная объясняющая переменная (переменные)

2. Статистика Дарбина-Уотсона

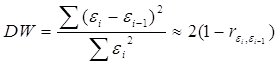
Очевидно:

0 £ DW £ 4

Если DW близко к нулю, это позволяет предполагать наличие положительной автокорреляции, если близко к 4 – отрицательной.

Распределение DW зависит от наблюденных значений, поэтому получить однозначный критерий, при выполнении которого DW считается «хорошим», а при невыполнении - «плохим», нельзя. Однако, для различных величин n и g найдены верхние и нижние границы, DW_L и DW_U, которые в ряде случаев позволяют с уверенностью судить о наличии (отсутствии) автокорреляции в модели. Правило:

1) При DW < 2:

а) если DW < DW_L – делаем вывод о наличии положительной автокорреляции (с вероятностью 1-g);

б) если DW > DW_U – делаем вывод об отсутствии автокорреляции (с вероятностью 1-g);

в) если DW_L £ DW £ DW_U – нельзя сделать никакого вывода;

2) При DW > 2:

а) если (4 – DW) < DW_L – делаем вывод о наличии отрицательной автокорреляции (с вероятностью 1-g);

б) если (4 – DW) > DW_U – делаем вывод об отсутствии автокорреляции (с вероятностью 1-g);

в) если DW_L £ (4 – DW) £ DW_U – нельзя сделать никакого вывода;

8. Гетероскедастичность остатков.

Возможные причины:

- ошибки в исходных данных;

- наличие закономерностей;

Обнаружение – возможны различные тесты. Наиболее простой:

(упрощенный тест Голдфелда – Куандта)

1) упорядочиваем выборку по возрастанию одной из объясняющих переменных;

2) формулируем гипотезу Н₀: остатки гомоскедастичны

3) делим выборку приблизительно на три части, выделяя k остатков, соответствующих «маленьким» х и k остатков, соответствующих «большим» х (k»n/3);

4) строим модели парной линейной регрессии отдельно для «меньшей» и «большей» частей

5) оцениваем дисперсии остатков в «меньшей» (s²₁) и «большей» (s²₁) частях;

6) рассчитываем дисперсионное соотношение:

7) определяем табличное значение F-статистики Фишера с (k–m–1) степенями свободы числителя и (k - m - 1) степенями свободы знаменателя при заданном уровне значимости g

8) если дисперсионное соотношение не превышает табличное значение F-статистики (т. е., оно подчиняется F-распределению Фишера с (k–m–1) степенями свободы числителя и (k - m - 1) степенями свободы знаменателя), то гипотеза Н₀ не отвергается - делаем вывод о гомоскедастичности остатков. Иначе – предполагаем их гетероскедатичность.

Метод устранения: взвешенный МНК.

Идея: если значения х оказывают какое-то воздействие на величину остатков, то можно ввести в модель некие «весовые коэффициенты», чтобы свести это влияние к нулю.

Например, если предположить, что величина остатка e_i пропорциональна значению x_i (т. е., дисперсия остатков пропорциональна x_i²), то можно перестроить модель следующим образом:

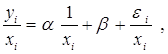
т. е. перейдем к модели наблюдений

где

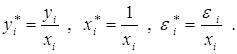
Таким образом, задача оценки параметров уравнения регрессии методом наименьших квадратов сводится к минимизации функции:

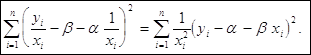
или

где - весовой коэффициент.