Реферат: Структура графа состояний клеточных автоматов определённого типа
Управление образования Московского района г. Минска
Государственное учреждение образования СШ № 41 г. Минска
Структура графа состояний клеточных автоматов определённого типа
Минск, 2009 г
Оглавление
§1 Введение
§1.1 Общие сведенья по клеточным автоматам
§2 Структура графа состояний для линейного оператора над Zp
§3 ACS-автомат
§3.1 Постановка задачи.
§3.2 Краткий обзор предыдущих результатов
§3.3 Структура Gj при p=2
§3.3.1 Исследование структуры
§3.3.2 Исследование высоты деревьев
§3.4 Структура Gj при p¹2
§4 Структура графа состояний оператора взятия разностей
§5 Перспективы исследования
§6 Резюме
Используемые источники. Список использованной литературы
§1 Введение
§1.1 Общие сведенья по клеточным автоматам
Клеточный автомат – это математический объект с дискретным пространством и временем. Каждое положение в пространстве представлено отдельной клеткой, а каждый момент времени – дискретным шагом или поколением. Состояние каждой клетки определяется некоторыми правилами взаимодействия. Эти правила предписывают изменения состояния каждой клетки в следующем такте времени в ответ на текущее состояние соседних клеток.
Общие правила построения клеточных автоматов:
1. Состояние клеток дискретно (0 или 1, но могут быть автоматы и с большим числом состояний).
2. Соседями является ограниченное число клеток.
3. Правила, задающие динамику развития клеточного автомата, имеют некоторую функциональную форму.
4. Клеточный автомат является тактируемой системой, т.е. смена клеток происходит одновременно.
Условные обозначения
| V(G) | Множество вершин графа G |
| E(G) | Множество ребер графа G |
|
|
Поддерево g с корнем v |
|
|
Множество вершин полного корневого поддерева g с корнем v дерева G, находящихся на m-том ярусе, относительно корня v. |
|
D( |
Множество висячих вершин графа |
|
|
Поле вычетов по mod p (p – простое), т.е. {1,2,..,p-1} |
|
|
|
Некоторые стандартные
обозначения векторов из ![]()
| (0,0,0,…,0)= |
en |
(1,0,1,1,0,1,…,0,1)= |
rn для n=2k+1 |
| (1,0,0,…,0)= |
dn |
(1,1,0,1,1,0,…,1,1)= |
sn для n=3k+2 |
Цели:
1.
Исследовать
структуру графа ![]() :
:
· определить количество и высоту деревьев, описать их структуру;
·
определить
количество и длину циклов графа ![]() ;
;
·
описать
множество висячих вершин графа ![]() .
.
2. Рассмотреть те же вопросы для случая произвольного линейного оператора.
§2 Структура графа состояний для линейного оператора над Zp
Введение
Рассмотрим множество ![]() и линейный оператор
и линейный оператор ![]() такое, что y
– линейный оператор над полем Zp,
в частности, этот оператор может задавать изменение состояния некоторого
одномерного клеточного автомата с p
состояниями.
такое, что y
– линейный оператор над полем Zp,
в частности, этот оператор может задавать изменение состояния некоторого
одномерного клеточного автомата с p
состояниями.
Будем рассматривать
граф состояний ![]() , для которого
, для которого
![]() . Основной целью
исследования является изучение структуры графа
. Основной целью
исследования является изучение структуры графа ![]() .
.
Одним из важных свойств оператора y, которое будет использоваться в дальнейшем, является его аддитивность:
![]()
Для исследования структуры графа Gy рассмотрим следующую нумерацию вершин нулевого дерева (см. рис. 2.1).
![]() – вершина, находящаяся
на m ярусе, при этом она входит в
– вершина, находящаяся
на m ярусе, при этом она входит в ![]()
(![]() ), смысл этих
обозначений станет ясным позже. Важно то, что в этих обозначениях в вершину
), смысл этих
обозначений станет ясным позже. Важно то, что в этих обозначениях в вершину ![]() входят
входят ![]() , при этом вершины
, при этом вершины ![]() входят в
входят в ![]() (в нашем случае.
(в нашем случае.
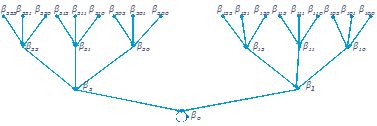
Рис. 2.1
Теорема 2.1
Пусть
задана цепь: ![]() тогда
тогда
![]() .
.
Доказательство:
Воспользуемся методом математической индукции.
База m=1:
![]()
![]() , действительно
, действительно ![]() причем
причем ![]() различные
вершины, ч.т.д.
различные
вершины, ч.т.д.
Пусть теорема верна для
m = l-1,
т.е![]() .
.
Докажем, что ![]() Тем, самым, по построению
Тем, самым, по построению ![]() , мы покажем, что
, мы покажем, что ![]() .
.
Действительно, в силу
линейности![]() :
:
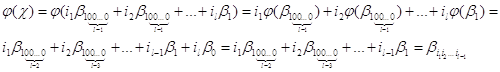
Теорема 2.1 доказана.
Назовем дерево с корнем en = (0,0,…,0) – «нулевым» деревом, тогда для него верна следующая теорема.
Теорема 2.2
«Нулевое» дерево – p-нарное дерево с точностью до петли в корне (0,0..,0).
Доказательство:
По теореме 2.1 единственная цепь из висячей вершины в (0,0,..0) однозначным образом определяет все элементы дерева (различность определяемых вершин очевидна, и следует из простоты p).
Теорема 2.3
Каждое дерево притягиваемого каждой точкой каждого цикла графа Gy изоморфно нулевому» дереву.
Доказательство:
Для любых последовательностей k и l, находящихся на одном ярусе какого-то дерева, для которых выполняется условие:
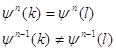
верно равенство:
![]() ,
,
где ![]() ―одна из последовательностей «нулевого» дерева на n-ном ярусе (сумма в поле
―одна из последовательностей «нулевого» дерева на n-ном ярусе (сумма в поле ![]() ) (Следует из теоремы 2.1).
) (Следует из теоремы 2.1).
Используя полученное соотношение можно достроить любое дерево до дерева изоморфного «нулевому».
§3 ACS-автомат
§3.1 Постановка задачи
В данной работе рассматривается клеточный автомат (одномерный), функционирование которого осуществляется по следующим правилам:
Дана
полоска 1![]() n
(сам автомат), все клетки, которой находятся в состояниях «0» и «1». Изменение
состояния клетки определяется следующим образом: данная клетка переходит в
состояние «1», если её соседи находятся в разных состояниях, и в «0»,если её
соседи находятся в одинаковых состояниях. Клетки, находящиеся по краям
переходят в то же состояние, которое было у единственной соседней клетки в
предыдущий момент времени.
n
(сам автомат), все клетки, которой находятся в состояниях «0» и «1». Изменение
состояния клетки определяется следующим образом: данная клетка переходит в
состояние «1», если её соседи находятся в разных состояниях, и в «0»,если её
соседи находятся в одинаковых состояниях. Клетки, находящиеся по краям
переходят в то же состояние, которое было у единственной соседней клетки в
предыдущий момент времени.
По полоске длины n
будем определять вектор ![]() ,
где
,
где ![]() :
:
![]()
Рассмотрим множество ![]() и отображение
и отображение ![]() такое, что
такое, что
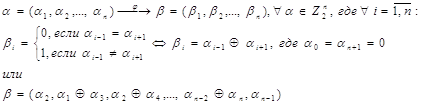
(здесь и ниже ![]() – операция сложения по mod
p=2, т.е. операция сложения в поле Z2).
– операция сложения по mod
p=2, т.е. операция сложения в поле Z2).
Будем рассматривать граф
состояний ![]() , для которого
, для которого ![]() . Основной целью исследования
является изучение структуры графа
. Основной целью исследования
является изучение структуры графа ![]() .
.
Для начала рассмотрим некоторые определения и обозначения, которые будут использоваться в дальнейшем в работе:
· Ориентированное дерево — это ориентированный граф без циклов, в котором из каждой вершины, кроме одной, называемой корнем ориентированного дерева, выходит ровно одно ребро (более подробно структуры дерева будет определена позже).
· m-й ярус – множество вершин дерева, находящихся на расстоянии m от корня.
·
Частичный порядок
на вершинах: ![]() , если вершины
u и v различны и вершина u лежит на единственном элементарном пути, соединяющем
вершиной v с корнем дерева.
, если вершины
u и v различны и вершина u лежит на единственном элементарном пути, соединяющем
вершиной v с корнем дерева.
·
Корневое
поддерево с корнем v — подграф ![]() .
.
·
Множество ![]() назовем множеством висячих
вершин графа
назовем множеством висячих
вершин графа ![]() .
.
§3.2 Краткий обзор предыдущих результатов
В прошлом году на ряде конференций (см. Используемые источники) была представлена работа по клеточным автоматам, в которой был исследован частный случай линейного оператора и найдены высоты деревьев для последовательностей, состоящих из 2n-1 элементов. В ней были представлены следующие утверждения, которые будут использоваться в дальнейшем:
Утверждение 3.2.1
![]() .
.
Утверждение 3.2.2
1.
![]() ;
;
2.
![]() , причем
, причем ![]()
![]()
3.
![]() ;
;
4.
![]() .
.
Утверждение 3.2.3
![]() ;
; ![]() и
и ![]() .
.
Предисловие
В параграфе будет рассказано о свойствах графа состояний оператора j, а именно будет описана его структура.
§3.3 Структура Gj при p=2
§3.3.1 Исследование структуры
Пользуясь утверждением 3.2.2, мы получаем, что среди всех последовательностей можно выделить следующие:
1. которые невозможно получить не из каких других, например: (1,0,0) (они будут образовывать висячие вершины графа);
2. которые, спустя несколько итераций возвращаются в начальное положение, например:
(1,0,0,0) ® (0,1,0,0) ® (1,0,1,0) ® (0,0,0,1) ® (0,0,1,0) ® (0,1,0,1) ® (1,0,0,0)
(такие последовательности в графе будут соответствовать вершинам цикла)
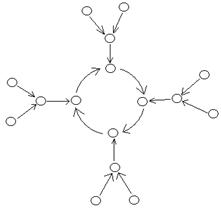
Используя утверждение 3.2.2, можно сделать вывод:
Теорема 3.3.1.1
Каждая
компонента связности графа ![]() является
циклом (возможно длины 1), каждый элемент которого притягивает дерево (т.е.
является корнем ориентированного дерева) (см. рис. 3.2.1).
является
циклом (возможно длины 1), каждый элемент которого притягивает дерево (т.е.
является корнем ориентированного дерева) (см. рис. 3.2.1).
Наша основная задача определить длины циклов и высоты деревьев, описать их структуру и найти их количество.
|
Теорема 3.3.1.2
Для любых последовательностей k и l, находящихся на одном ярусе
какого-то дерева, для которых выполняется условие: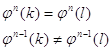 верно равенство:
верно равенство:
![]() , где
, где ![]() ―одна из последовательностей «нулевого» дерева на n-ном ярусе.
―одна из последовательностей «нулевого» дерева на n-ном ярусе.
Более точно это можно сформулировать так:
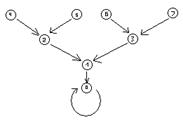
Рис. 3.2.2
Для
любого «полного» корневого поддерева g
с корнем v дерева G
(с корнем в ![]() ):
): ![]() , где
, где ![]() и
и ![]() –
подмножество
–
подмножество ![]() такое, что:
такое, что: ![]()
![]() , при этом
, при этом ![]() (см. рис. 3.2.2).
(см. рис. 3.2.2).
Доказательство
Воспользуемся методом математической индукции:
1. m = 1:
Пусть
![]() , тогда
, тогда ![]() . Тогда, учитывая утверждение 1.1,
. Тогда, учитывая утверждение 1.1, ![]() и
и ![]() , получим требуемое.
, получим требуемое.
2. Пусть утверждение леммы верно для m = k, тогда:
3. Докажем теорему для m = k+1.
Мы
имеем: ![]() , тогда:
, тогда:
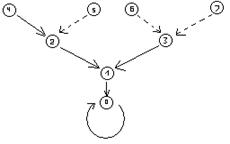
Если
![]() и
и ![]() , то
, то![]() :
:
Из утверждения 3.2.1:
![]() ,
но
,
но ![]() ,
т.е.
,
т.е. ![]() , откуда
, откуда ![]() , ч.т.д.
, ч.т.д.
Теорема 3.3.1.3
«Нулевое» дерево ― бинарное дерево с точностью до петли в корне en.
Доказательство:
|
Теорема 3.3.1.4
Все деревья (в том числе и примыкающие к каждой вершине произвольного цикла) будут иметь столько ярусов, сколько и «нулевое», причем будут иметь такую же структуру.
Более точно: дерево, притягиваемое каждой точкой каждого цикла графа состояний, изоморфно дереву, притягиваемому точкой en.
Доказательство:
Предположим «нулевое» дерево состоит из n ярусов тогда:
1. Если наше дерево состоит менее чем из n ярусов, то, пользуясь теоремой 3.3.1.2, мы восстанавливаем его до дерева изоморфного «нулевому».
2.
Если
дерево имеет m ярусов, где n<m
тогда ![]() , получается,
что «нулевое» дерево состоит из m
ярусов Ї противоречие.
, получается,
что «нулевое» дерево состоит из m
ярусов Ї противоречие.
§3.3.2 Исследование высоты деревьев
Теорема 3.3.2.1
Если длина последовательности равна 2k-1, то высота деревьев будет равна 2k-1.
Доказательство:
Пример для k=1 и k=2 строятся довольно просто:
k=1 k=2
0 (1) 0 0 (1,0,0) 0
0 (0) 0 0 (0,1,0) 0
0 (1,0,1) 0
0 (0,0,0) 0
Докажем по индукции
1. База индукции:
Пусть k=3, тогда:
0 (1,0,0,0,0,0,0) 0
0 (0,1,0,0,0,0,0) 0
0 (1,0,1,0,0,0,0) 0
0 (0,0,0,1,0,0,0) 0
0 (0,0,1,0,1,0,0) 0
0 (0,1,0,0,0,1,0) 0
0 (1,0,1,0,1,0,1) 0
0 (0,0,0,0,0,0,0) 0
Высота дерева равна 2k=7.
2. Пусть утверждение верно для n=k, тогда докажем его для n=k+1:
![]() ;
;
тогда:
![]()
![]()
Так
как ![]() -й элемент равен
«0» и остальные элементы симметричны относительно его, то в каждом последующем
поколении этот элемент будет равен «0», следовательно, правая и левая части
перейдут в состояние (0,0,…,0) через 2k
поколений. Таким образом, высота дерева будет 2k
+2k-1=2k+1-1=2n-1
ч.т.д.
-й элемент равен
«0» и остальные элементы симметричны относительно его, то в каждом последующем
поколении этот элемент будет равен «0», следовательно, правая и левая части
перейдут в состояние (0,0,…,0) через 2k
поколений. Таким образом, высота дерева будет 2k
+2k-1=2k+1-1=2n-1
ч.т.д.
Теорема 3.3.2.2
Если длину
последовательности представить в виде ![]() где
где ![]()
![]() ,
тогда 2k-1
Ї высота «нулевого» дерева.
,
тогда 2k-1
Ї высота «нулевого» дерева.
Доказательство:

По
теореме 3.3.2.1 ![]() , где
, где ![]() с корнем
с корнем ![]() .
.
Возьмем
последовательность ![]() длиной
длиной ![]() ;
; ![]()
![]()
![]() заметим, что
заметим, что ![]() тогда:
тогда:
![]() (в связи с
симметрией относительно
(в связи с
симметрией относительно ![]() )
)
Но тогда:
Высота
дерева при n=2n-1
равна высоте дерева при n=3×2n-1.
В связи с симметрией относительно ![]() , мы получаем:
, мы получаем:
Высота дерева при n=2n+1+2n-1-1 равна высоте дерева при n=3×2n-1-1.
Таким
образом, мы получаем, что если представить длины последовательности в виде: ![]() , то 2-1k
Ї высота дерева.
, то 2-1k
Ї высота дерева.
Теорема доказана.
§3.4 Структура Gj при p¹2
Введение
В
параграфе 2 мы рассматривали структуру графа состояний для произвольного
линейного оператора над Zp.
В данном параграфе пойдет речь о структуре графа Gj
определенного в параграфе 3.1. По аналогии со случаем p=2,
по состоянию числовой полоски длины n
(т.е. самого автомата с состояниями 0,1,..p-1)
будем определять вектор![]() , и
рассматривать
, и
рассматривать ![]() такое, что:
такое, что:
![]()
Все остальные основные определения вводятся аналогичным образом, как и в случае p=2, основным предметом исследования является структура графа Gj.
Одним из важных свойств оператора j является его аддитивность:
![]()
которая следует из линейности оператора j.
В предыдущем параграфе было доказано утверждение о том, что для произвольного линейного оператора y «нулевое» дерево – p-нарное дерево с точностью до петли в корне (0,0..,0) (теорема 2.2). В данном параграфе будет определена высота нулевого дерева, тем самым будут определена высота дерева притягиваемого каждой точкой каждого цикла графа Gj (теорема 2.3).
Теорема 3.4.0
Вершина
![]() является висячей тогда и
только тогда, когда n – нечётное и
выполняется условие:
является висячей тогда и
только тогда, когда n – нечётное и
выполняется условие:
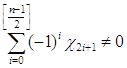
Доказательство:
Пусть
у нас есть последовательности ![]() и
и ![]()
Тогда
![]() Но тогда
Но тогда ![]() .
.
Но
по условию ![]() , т.е. для того
чтобы вершина
, т.е. для того
чтобы вершина ![]() была висячей
необходимо и достаточно, чтобы
была висячей
необходимо и достаточно, чтобы ![]() , т.е.
, т.е.
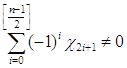
Теорема полностью доказана.
Теорема 3.4.1
Если длина последовательности кратна двум, то граф Gφ ― дизъюнктное объединение циклов.
Доказательство:
Воспользуемся
тем, что дерево, притягиваемое каждой точкой каждого цикла, изоморфно нулевому
дереву. Рассмотрим нулевое дерево. Его высота при n=2k
равна нулю. Это следует из того, что ![]() , но m=2s+1,
противоречие. Теорема полностью доказана.
, но m=2s+1,
противоречие. Теорема полностью доказана.
Теорема 3.4.2
Если длину последовательности представить в виде pk(2l)-1, (p,l)=1, тогда pk есть высота «нулевого» дерева.
Доказательство:
Для начала докажем следующие леммы.
Лемма 1
![]() – висячая вершина
причем,
– висячая вершина
причем, ![]() .
.
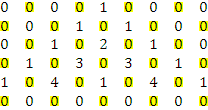
Рис. 3.4.1 Пример для p = 5.
Доказательство леммы 1:
Для начала рассмотрим
шахматную раскраску таблицы (2pk-1)(pk+1),
строки которой есть последовательности ![]() ,
, ![]() , …,
, …, ![]() (см. рис.).
Тогда числа, стоящие на закрашенных позициях равны 0.
(см. рис.).
Тогда числа, стоящие на закрашенных позициях равны 0.
Остальные координаты
образуют треугольник Паскаля с вершиной в 1 (см. пример на рис. 3.4.1 для p
= 5). Тогда т.к. ![]() , то:
, то:
![]() ,
,
при этом ![]() (все значения
биноминальных коэффициентов берутся по модулю p,
так как мы рассматриваем вектор в пространстве
(все значения
биноминальных коэффициентов берутся по модулю p,
так как мы рассматриваем вектор в пространстве ![]() )
)
Замечание:
Здесь и ниже, все
многочлены рассматриваются над полем ![]()
Докажем, что ![]()
Действительно, т.к.
![]() (т.к.
(т.к.
![]() ), то:
), то: ![]() .
.
Откуда ![]() , ч.т.д.
, ч.т.д.
Замечание
Висячесть вершины ![]() следует из
теоремы 3.4.0
следует из
теоремы 3.4.0
Следствие
![]() – висячая вершина
– висячая вершина ![]() причем,
причем, ![]() .
.
Для доказательства домножим элементы рассмотренного выше треугольник Паскаля на i и в силу простоты p получим требуемое.
Лемма 2
Вершина н вида:
![]()
является висячей при
условии, что число последовательностей вида ![]() , где
, где ![]() не кратно p,
причем
не кратно p,
причем ![]() .
.
Доказательство леммы 2:
Из теоремы 3.4.0,
вершина ![]() является висячей
при n нечётном и выполнении
условия:
является висячей
при n нечётном и выполнении
условия:
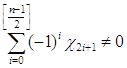 .
.
Таким образом, при подстановке соответствующих значений получим:
![]() .
.
![]() , где
, где ![]() .
.
Таким образом, вершина вида:
![]()
является висячей при
условии, что число конструкций вида ![]() , где m=1
либо (p-1), не кратно p.
Вторая часть леммы следует из следствия леммы 1, причем, как и в лемме 1,
, где m=1
либо (p-1), не кратно p.
Вторая часть леммы следует из следствия леммы 1, причем, как и в лемме 1, ![]() Лемма доказана.
Лемма доказана.
Приступим теперь к
доказательству основной теоремы. Из леммы 1 следует, что высота дерева при ![]() равна pk,
из леммы 2 следует, что если высота дерева при
равна pk,
из леммы 2 следует, что если высота дерева при ![]() равна высоте дерева
при
равна высоте дерева
при ![]() и, при условии,
что (l,p)=1.
и, при условии,
что (l,p)=1.
Теорема полностью доказана.
§4 Структура графа состояний оператора взятия разностей
Введение
В
данном параграфе рассматривается структура графа состояний Gw
оператора взятия разностей ![]() (см.
[1]), который определяется следующим образом:
(см.
[1]), который определяется следующим образом:

В ([1]) w был рассмотрен только над Z2, в этом параграфе оператор взятия разностей будет рассмотрен над полем Zp. Оператор взятия разностей используется для анализа сложности функций (см. [1]).
На основе результатов параграфа 2 (теоремы 2.2, 2.3), для анализа структуры графа состояний оператора w достаточно определить высоту нулевого дерева, тем самым будут определена высота дерева притягиваемого каждой точкой каждого цикла графа Gw (теорема 2.3).
Теорема 4.1
Если
![]() , то наименьший
период функции
, то наименьший
период функции ![]() (mod
p) по i
равен pk.
(mod
p) по i
равен pk.
Доказательство
Проверим
сначала, что число pk
является периодом при ![]() :
:
![]()
Действительно,
т.к.:![]()
![]() ,
,
то
![]() , ч.т.д.
, ч.т.д.
Теперь
покажем, что это наименьший период, если ![]() , наименьший период
должен быть делителем числа pk,
поэтому мы проверим, что pk-1
– не период.
, наименьший период
должен быть делителем числа pk,
поэтому мы проверим, что pk-1
– не период.
Докажем,
что при ![]() число сочетаний
число сочетаний ![]() , действительно,
пусть j= i-(p-1)pk-1,
тогда
, действительно,
пусть j= i-(p-1)pk-1,
тогда ![]() . Тогда, т.к.:
. Тогда, т.к.:
![]() ,
,
откуда
т.к. ![]() и
и![]() , то
, то ![]() ,т.е.
,т.е. ![]() , ч.т.д.
, ч.т.д.
С
другой стороны ![]() , поэтому число pk-1
не является периодом функции
, поэтому число pk-1
не является периодом функции
![]() (mod
p) по переменной i,
когда
(mod
p) по переменной i,
когда ![]() , при этом
условии
, при этом
условии ![]() .
.
Теорема 4.2
Если
длину последовательности представить в виде: ![]() где
где ![]()
![]() ,
,
![]() , тогда pk есть
высота «нулевого» дерева.
, тогда pk есть
высота «нулевого» дерева.
Доказательство
Проведем явное
интегрирование функции ![]() периода
n, т.е. определим a,
такое, что j(a) = (1,1,…,1) (строгое определение
интегрирования см. в [1])
периода
n, т.е. определим a,
такое, что j(a) = (1,1,…,1) (строгое определение
интегрирования см. в [1])
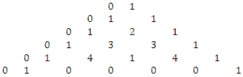
Рис. 4.1
Легко видеть, что все
интегрированные «интегралы» (с начальным условием ![]() при t=1)
– это приведенные по модулю p
косые линии треугольника Паскаля, на которых j
= 0 для исходной функции
при t=1)
– это приведенные по модулю p
косые линии треугольника Паскаля, на которых j
= 0 для исходной функции ![]() , а затем, по мере
повторного «интегрирования», ответы доставляют косые линии с j
= 0,1,2… (см рис. 4.1)
, а затем, по мере
повторного «интегрирования», ответы доставляют косые линии с j
= 0,1,2… (см рис. 4.1)
Следовательно, для
выяснения того, сколько раз удастся «проинтегрировать» функцию ![]() (т.е.
определить высоту нулевого дерева) в классе n-периодических
функций (т.е. в классе n-периодических
последовательностей) остается выяснить, при каких значениях j
функция
(т.е.
определить высоту нулевого дерева) в классе n-периодических
функций (т.е. в классе n-периодических
последовательностей) остается выяснить, при каких значениях j
функция ![]() аргумента i
будет иметь период n.
аргумента i
будет иметь период n.
В
силу теоремы 4.1, если n=![]()
![]() , то построение «нулевого» дерева, описанного выше,
будет успешным до тех пор, пока «j-кратные
интегралы»
, то построение «нулевого» дерева, описанного выше,
будет успешным до тех пор, пока «j-кратные
интегралы» ![]() от функции
от функции ![]() будут
оставаться n-периодическими
функциями аргумента i. Но наименьший
период указанной функции переменной i
равен pr
при
будут
оставаться n-периодическими
функциями аргумента i. Но наименьший
период указанной функции переменной i
равен pr
при ![]() . Чтобы эта функция была n-периодической,
необходимо, чтобы число n=
. Чтобы эта функция была n-периодической,
необходимо, чтобы число n=![]() делилось на наименьший период,
т.е. чтобы
делилось на наименьший период,
т.е. чтобы ![]() . Откуда следует, что если длину
последовательности представить в виде: n=
. Откуда следует, что если длину
последовательности представить в виде: n=![]()
![]() , тогда pk есть высота «нулевого» дерева,
ч.т.д.
, тогда pk есть высота «нулевого» дерева,
ч.т.д.
§5 Перспективы исследования
1.
Более подробно
исследовать структуру ![]() , а
именно:
, а
именно:
· Определить количество циклов и их длину;
· Описать множество корней деревьев и т.д.
2.
Рассмотреть
двумерный вариант клеточного автомата (на клеточном прямоугольнике ![]() ) с теми же вопросами, т.е.
описать структуру графа состояний.
) с теми же вопросами, т.е.
описать структуру графа состояний.
3. Более подробно рассмотреть матричную интерпретацию.
4. В связи с использованием одномерных клеточных автоматов, а также линейных операторов, в теории кодирования, найти количественные и качественные характеристики автомата (например, определить коллизии и т.д.).
5. В связи с тем, что некоторые правила «эквивалентны», изучить их относительно данного аспекта (т.е. найти некоторую «совместимость» между правилами). Определить условия эквивалентности правил, найти разбитие на классы эквивалентности. Данная задача является открытой проблемой.
§6 Резюме
Основным
предметом исследования являлась рассмотрение структуры графа ![]() , более подробное изучение которой,
является одним из наиболее перспективных направлений дальнейшего исследования.
В общем случае получена следующая характеристика структуры графа
, более подробное изучение которой,
является одним из наиболее перспективных направлений дальнейшего исследования.
В общем случае получена следующая характеристика структуры графа ![]() :
:
1.
Каждая компонента связности графа ![]() является циклом (возможно длины
1), каждая вершина которого притягивает дерево (возможно нулевой высоты).
является циклом (возможно длины
1), каждая вершина которого притягивает дерево (возможно нулевой высоты).
2.
![]() и
и ![]()
![]() ;
;
3.
![]() ;
;
4. «Нулевое» дерево ― p-нарное дерево с точностью до петли в корне en (0,0..0), причем его высота равна
·
![]() (для оператора
(для оператора ![]() , описывающего функционирование ACS-автомата
и
, описывающего функционирование ACS-автомата
и ![]() ), если длину
последовательности представить в виде
), если длину
последовательности представить в виде ![]() где
где ![]() ,
, ![]() ;
;
·
![]() (для оператора
(для оператора ![]() , описывающего функционирование ACS-автомата
и
, описывающего функционирование ACS-автомата
и ![]() ) если длину
последовательности представить в виде:
) если длину
последовательности представить в виде: ![]() где
где ![]() ,
, ![]() .
.
5.
«Нулевое» дерево ― p-нарное
дерево с точностью до петли в корне en
(0,0..0), причем его высота равна ![]() (для оператора взятия разности), если длину последовательности
представить в виде:
(для оператора взятия разности), если длину последовательности
представить в виде: ![]() где
где ![]()
![]() ,
,
![]() ;
;
6. Все деревья (в том числе притягиваемые каждой вершиной каждого цикла) будут иметь столько ярусов, сколько и «нулевое», причем будут иметь такую же структуру. Т.е. дерево, притягиваемое каждой точкой каждого цикла графа состояний, изоморфно дереву, притягиваемому точкой en (0,0..0).
Используемые источники. Список использованной литературы
Используемые источники
1. М.С. Глущенко, П.С. Пересторонин, Почти центральная симметрия (доклад на IV Балтийском научно–инженерном конкурсе, Санкт-Петербург, 2008 г.)
2. М.С. Глущенко, П.С. Пересторонин, Почти центральная симметрия (доклад на XII Белорусской республиканской конференции учащихся общеобразовательных учреждений, Минск, 2008 г.)
Список использованной литературы
1. В.И. Арнольд, Сложность конечных последовательностей нулей и единиц и геометрия конечных функциональных пространств (из доклада Московскому математическому Обществу 22 ноября 2005 г.)
2. В.И. Арнольд, Топология и статистика арифметических и алгебраических формул, Успехи математических наук 58(2003), №4, 3-28