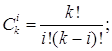Лабораторная работа: Метод конечных разностей

Лабораторная работа

Метод конечных разностей

Цель работы

Ознакомиться с аналоговым и дискретным вариантами реализации фильтра

Общие сведения

Если известны значения некоторой функции  для равноотстоящих значений аргумента

,

где .

Здесь

Тогда можно говорить, что задана таблица функции  с шагом , начальным значением аргумента  и конечным значением аргумента .

Конечными разностями первого порядка функции называются числа

Аналогично определяются конечные разности второго порядка

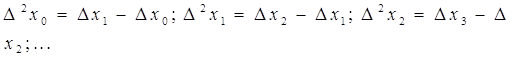
Тогда разности порядка определяются соотношениями

Таблица значений функции и её конечных разностей

Таким образом, все разности чётного порядка располагаются в тех же (горизонтальных) строчках, что и аргументы, все нечётные разности располагаются в промежуточных строчках.

При программной реализации воспользуемся методом четвёртых разностей

Представим график исследуемой функции в следующем виде

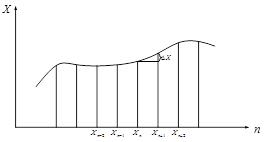
Разность первого порядка здесь будет определяться следующим выражением:

Разность второго порядка с учётом предыдущего выражения примет вид:

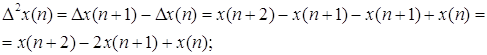
Аналогично определяются разности третьего и четвёртого порядков. Выполнив подстановку и приведение подобных получим следующие выражения:

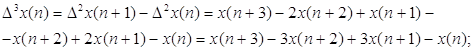
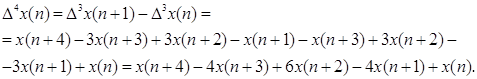
В обобщённом виде рекуррентное соотношение для вычисления сглаженного значения полезного сигнала в очередном i-том цикле расчёта:

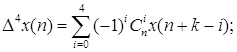
где