Контрольная работа: Методы расчета сложных электрических цепей
Уральский государственный технический университет – УПИ
Кафедра автоматики и управления в технических системах
Методы расчета
сложных электрических цепей
Екатеринбург
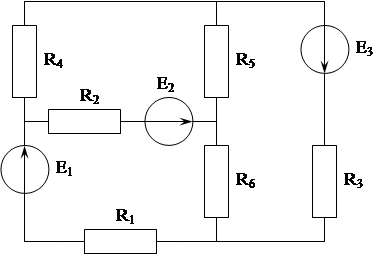
Расчетное задание
Для заданной электрической цепи, в которой ![]() ,
, ![]() , а остальные параметры
указаны в таблице, требуется рассчитать:
, а остальные параметры
указаны в таблице, требуется рассчитать:
· все токи и напряжения методом контурных токов;
· все токи и напряжения методом узловых напряжений;
· ток через сопротивление R6 методом эквивалентного генератора.
| Номер схемы |
|
|
|
|
|
|
|
| 2 | 8 | 16 | 5 | 91 | 180 | 100 | 120 |
Метод контурных токов
Составим систему для метода контурных токов:
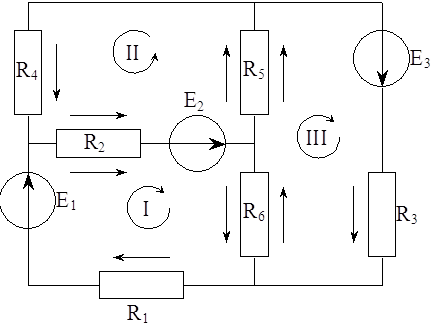
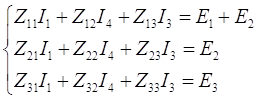 (1)
(1)
Найдем собственные и взаимные сопротивления контуров:
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
Подставим найденные значения ![]() и данные значения
и данные значения ![]() в
систему (1):
в
систему (1):
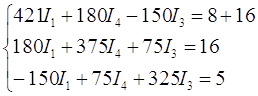
Решая систему, находим:
![]() ,
, ![]() ,
,
![]() .
.
Из схемы видно, что:
![]() ,
, ![]() ,
,![]() .
.
Соответственно, значения напряжений
(рассчитываем по закону Ома: ![]() ):
):
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,![]() .
.
Метод узловых напряжений
Прежде, чем применять метод узловых напряжений, преобразуем все источники напряжения в эквивалентные источники тока:
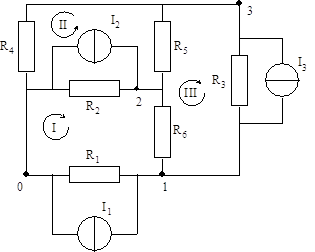
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
![]() .
.
Рассчитаем собственную и взаимную проводимости:
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
Найдем токи в источниках по формуле ![]() :
:
![]() ,
, ![]() ,
,
![]() .
.
Запишем узловые токи:
![]() ,
, ![]() ,
,
![]() .
.
Составим систему для метода узловых напряжений:
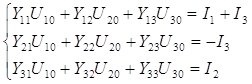 (2)
(2)
Подставим найденные значения ![]() и
и ![]() в систему (2):
в систему (2):
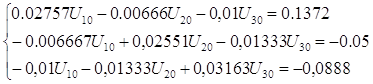
Решая систему, находим:
![]() ,
,
![]() ,
, ![]() .
.
Из схемы видно, что:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Соответственно, значения сил токов
(рассчитываем по закону Ома: ![]() ):
):
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
![]() .
.
Метод эквивалентных источников
С помощью эквивалентных преобразований, заменим исходную схему на следующую:
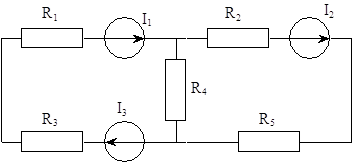
Для этого, рассчитаем напряжение между точкам А и Б методом контурных токов:
Контурные уравнения:
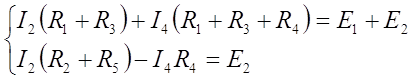
Тогда, эти уравнения и имеют матричный вид:
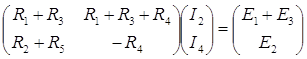
Подставим конкретные значения:
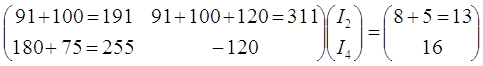
Из решения этой системы, имеем:
![]()
![]() .
.
Выразим токи в ветвях через контурные токи:
![]()
Подставим конкретные значения:
![]()
Найдем напряжение на отрезке АБ:
![]()
Замкнем все источники напряжения и найдем входное сопротивление внешней цепи:
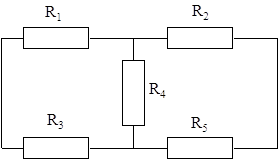
Рассчитаем сопротивление полученной цепи. Для этого преобразуем ее следующим образом:
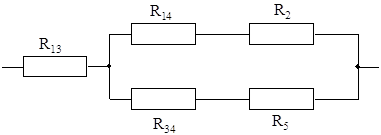
Рассчитаем сопротивления R13, R14, R34:
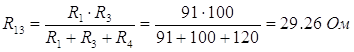
![]()
![]()
Найдем общее сопротивление цепи:
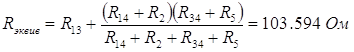
Заменим внешнюю, по отношению к ветви, цепь, содержащую сопротивление R6, эквивалентным источником напряжения:
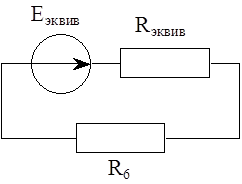
Тогда:
![]()
![]()
Результаты расчётов токов и напряжений в методе контурных токов практически совпали с результатами метода узловых напряжений, небольшие отклонения связаны с округлениями при вычислениях. Значение тока I6, найденное методом эквивалентного генератора, совпало со значениями, полученными в методах контурных токов. Это говорит о правильности расчётов.
1) Проектирование фильтра Баттерворта верхних частот:
Wp=2*pi*8e3 рад/с – частота, ограничивающая область подавления;
Ws=2*pi*1e4 рад/с – гарантированная частота области пропускания;
Rp=3 дБ – уровень полосы подавления;
Rs=30дБ – уровень полосы пропускания;
Построение АЧХ фильтра:
[n, Wc]=buttord (Wp, Ws, Rp, Rs, 's') – определение порядка фильтра и частоты на уровне 3 дБ;
[z, p, k]=buttap(n) – способ аппроксимации фильтра;
[b, a]=zp2tf (z, p, k) – низкочастотный прототип фильтра;
[bt, at]=lp2hp (b, a, Wc) – переход к высоким частотам;
f=linspace (0,2e4,100) – определение полосы частот;
k=freqs (bt, at, 2*pi*f) – модуль АЧХ;
plot (f, abs(k)) – построение АЧХ:
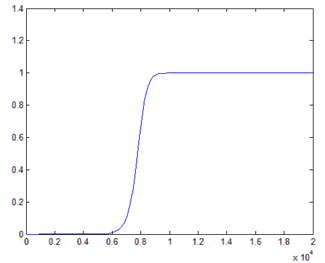
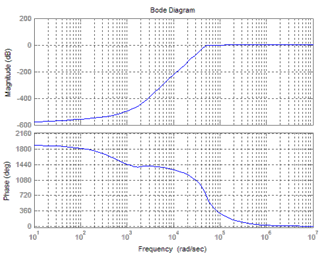
2) Построение фильтра, тип которого не известен:
m=[zeros (1,11), ones (1,5), linspace (0. 9,0,10)];
f=[0:25]*100;
plot (f, m):
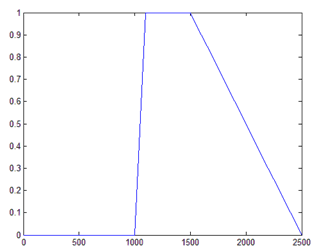
fn=[fn 1] – добавляем количество нормированных частот до 1;
m=[m 0] – количество амплитуд должно равняться количеству частот;
b=fir2 (100, fn, m);
k=freqz (b, 1, fn);
plot (fn, abs(k))
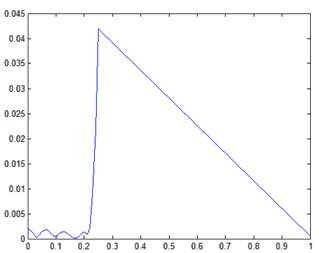
freqz (b, 1)
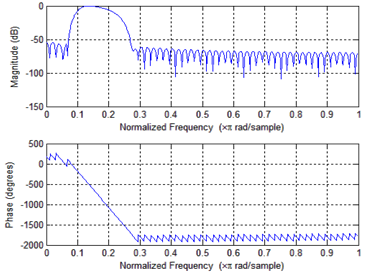
Вывод: В ходе лабораторной работы с помощью прикладного пакета MATLAB были спроектированы аналоговый фильтр Баттерворта верхних частот и произвольный фильтр. Графики, полученные в ходе проектирования прилагаются в отчете.