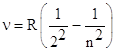Реферат: Квантовая теория атома
Квантовая теория атома
Исторически первая (классическая) модель строения атома была предложена в 1903 г. Томсоном. Согласно модели Томсона атом представляет собой шар, заряженный положительным электрическим зарядом непрерывно и равномерно, внутри которого около своих положений равновесия совершают колебания электроны. Суммарный отрицательный заряд всех электронов равен положительному заряду шара, и в целом атом электронейтрален. Приблизительные размеры такого положительно заряженного шара, определенные по классической электростатике, согласовывались с реальными размерами атомов (R ≈ 10-8 cм).
Действительно, если
напряженность электрического поля внутри шара ![]() , где е – положительный заряд шара, то «квазиупругая»
сила, действующая на электрон
, где е – положительный заряд шара, то «квазиупругая»
сила, действующая на электрон ![]() . Тогда электрон будет совершать колебания с
частотой
. Тогда электрон будет совершать колебания с
частотой 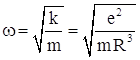 , и радиус
положительно заряженного шара можно оценить как
, и радиус
положительно заряженного шара можно оценить как 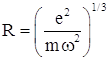 . Для наблюдаемых частот спектра излучения атомов (λ ≈ 0,6 мкм и ω ≈ 3·1015 рад/с) получаем величину R ≈ 3·10-8 cм.
. Для наблюдаемых частот спектра излучения атомов (λ ≈ 0,6 мкм и ω ≈ 3·1015 рад/с) получаем величину R ≈ 3·10-8 cм.

Однако эта модель была опровергнута экспериментами Э.Резерфорда (1911 г.) по рассеянию α – частиц при прохождении их через тонкие металлические фольги (α–частицы – это положительно заряженные (qα = +2qe ) частицы с массой mα ≈ 4mH, образующиеся, в частности, при радиоактивном распаде тяжелых элементов). Опыты показали, что наряду с большинством α – частиц, отклоняющихся незначительно от своего первоначального направления, наблюдалось некоторое число α – частиц, которые при прохождении через тонкую фольгу резко отклонялись на большие (φ ≈ 135О – 150О) углы.
Это соответствовало
упругому отражению α – частиц от положительно заряженного и массивного
твердого тела, расположенного на пути следования частиц. Заметного отклонения
из-за взаимодействия α – частиц с электронами не могло
быть, так как масса α
– частиц значительно (на
четыре порядка величины) больше массы электронов. Следовательно, отклонение α – частиц обусловлено воздействием на них атомных
ядер. Э.Резерфорд теоретически рассмотрел задачу о рассеянии α – частиц в кулоновском поле, создаваемом
положительным зарядом, сосредоточенным в ядре атома. Потенциальная энергия
взаимодействия α – частиц с таким ядром 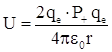 , где
, где ![]() – число положительных зарядов ядра. Число частиц,
рассеянных в единицу времени в единичный телесный угол dΩ (dΩ = sinΘ dΘ dφ ) определялось по формуле:
– число положительных зарядов ядра. Число частиц,
рассеянных в единицу времени в единичный телесный угол dΩ (dΩ = sinΘ dΘ dφ ) определялось по формуле: 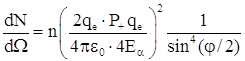 ,
,
где n – плотность потока α – частиц
(число частиц в единицу времени на единицу площади); φ – угол рассеяния α–частиц,
![]() – их энергия. Из формулы
следовало, что для данного материала фольги, плотности потока и определенной
энергии α–частиц
– их энергия. Из формулы
следовало, что для данного материала фольги, плотности потока и определенной
энергии α–частиц ![]() величина
величина ![]() , что и подтвердилось проведенными опытами.
, что и подтвердилось проведенными опытами.
Кроме того, формула
Резерфорда позволила определить число ![]() положительных зарядов в ядре атомов материала
рассеивающей фольги: оказалось, что
положительных зарядов в ядре атомов материала
рассеивающей фольги: оказалось, что ![]() равно Z – порядковому номеру элемента в периодической таблице Менделеева. При
этом из нейтральности атома непосредственно следовало, что число электронов в
атоме также равно Z .
равно Z – порядковому номеру элемента в периодической таблице Менделеева. При
этом из нейтральности атома непосредственно следовало, что число электронов в
атоме также равно Z .
На основании результатов экспериментов по рассеянию α–частиц тонкими металлическими фольгами Резерфорд предложил ядерную (или планетарную) модель атома: в ядре атома размером ~ 10-14÷10-15 м, т.е. в области размером много меньше размера атома (~ 10-10 м), сосредоточен весь положительный заряд Zqe и практически вся масса атома. Вокруг ядра в области ~ 10-10 м по замкнутым орбитам вращаются Z электронов. Суммарный положительный заряд, таким образом, равен суммарному отрицательному заряду, и в целом атом электронейтрален. Ядерная модель Резерфорда по своей структуре напоминает Солнечную систему: в центре системы массивное ядро – «солнце», вокруг него по орбитам вращаются планеты – электроны. Отсюда и второе название данной модели – «планетарная».
Резерфорд пришел к модели
с вращающимися вокруг ядра электронами вследствие того, что статическая модель
атома не может существовать. Согласно теореме Ирншоу классической
электростатики, система неподвижных электрических зарядов, расположенных на
конечном расстоянии друг от друга не могут находиться в состоянии устойчивого
равновесия только лишь под действием кулоновских сил. Однако модель с
вращающимися вокруг ядра электронами приводит к необходимости постоянного
излучения электронами атома электромагнитных волн. Рассмотрим, например,
движение электрона вокруг протона. По второму закону Ньютона 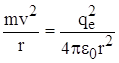 , и поскольку движение электрона
– равноускоренное, происходит излучение и постоянная потеря энергии. Следовательно,
электрон не может удержаться на круговой орбите и по спирали приближается к
ядру. При этом энергия уменьшается постепенно, частота излучения меняется по
непрерывному закону, и электромагнитное излучение атомов должно иметь сплошной
спектр. В действительности же излучение атомов представляет собой набор
отдельных линий, т.е. спектр излучения атомов – линейчатый.
, и поскольку движение электрона
– равноускоренное, происходит излучение и постоянная потеря энергии. Следовательно,
электрон не может удержаться на круговой орбите и по спирали приближается к
ядру. При этом энергия уменьшается постепенно, частота излучения меняется по
непрерывному закону, и электромагнитное излучение атомов должно иметь сплошной
спектр. В действительности же излучение атомов представляет собой набор
отдельных линий, т.е. спектр излучения атомов – линейчатый.
Таким образом, можно сформулировать следующие противоречия между классической моделью строения атома Резерфорда и реально наблюдаемыми явлениями:
| Согласно модели Резерфорда: | В действительности: |
| 1. Система «ядро – электрон» – неустойчива. | Атомы – устойчивые образования |
| 2. Электроны атомов излучают постоянно. | Атомы излучают только при определенных условиях. |
| 3. Спектр излучения атомов – сплошной. | Излучение атомов всегда имеет линейчатый спектр, зависящий от строения и свойств атомов различных веществ. |
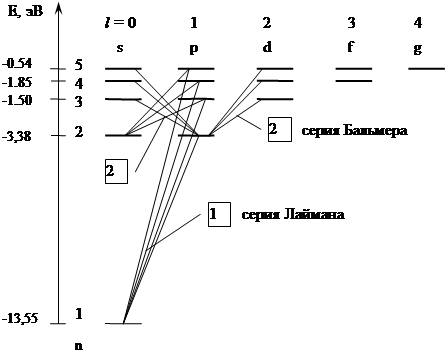
Итак, модель Резерфорда не могла объяснить, многочисленные экспериментальные результаты по изучению спектров излучения газов. Было известно, что спектры излучения газов представляют собой отдельные линии или группы (серии) близкорасположенных линий, причем каждому газу соответствует свой линейчатый спектр. И.Бальмер (1885 г.) исследовал спектр излучения водорода и установил, что спектр может быть описан следующей формулой (в дальнейшем называемой формулой Бальмера):
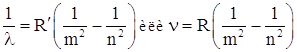 ,
,
где R = ![]() ·c = 3,29·1015
c-1 – постоянная Ридберга; m, n – целые числа.
·c = 3,29·1015
c-1 – постоянная Ридберга; m, n – целые числа.
При этом n = m+1, m+2, m +3 …, число m определяет серию, а n – отдельные линии в спектре.
При исследовании спектров излучения различных газов были получены следующие эмпирические формулы, подтверждавшие с высокой степенью точности экспериментальные данные, но не имевшие теоретического обоснования:
| m = 1 | серия Лаймана (УФ диапазон) |
|
n = 2, 3, 4 … |
| m = 2 | серия Бальмера (видимый диапазон) |
|
n = 3, 4, 5 … |
| m = 3 | серия Пашена (ИК диапазон) |
|
n = 4, 5, 6 … |
| m = 4 | серия Брэкета (ИК диапазон) |
|
n = 5, 6, 7 … |
| m = 5 | серия Пфунда (ИК диапазон) |
|
n = 6, 7, 8 … |
| m = 6 | серия Хэмфри (ИК диапазон) |
|
n = 7, 8, 9 … |
Вид формул, симметричность и повторяемость целых чисел (m, n), универсальность постоянной Ридберга привело к предположению об особой физической роли чисел m и n – квантовых чисел, определяющих параметры состояния атомов.
Первая неклассическая теория атома была предложена в 1913 г. Н.Бором. При этом Бор не отказался от описания поведения электронов в атоме законами классической физики. Но для того, чтобы совместить линейчатость спектров излучения атомов и ядерную модель Резерфорда, Бор в виде постулатов ввел некоторые предположения, которые, строго говоря, противоречили классической физике, и, тем не менее, приводили к абсолютно правильным результатам.
I постулат Бора (постулат стационарных состояний):
Существуют стационарные состояния атома, характеризующиеся определенными дискретными значениями энергии, в которых атом не излучает энергию.
Этим стационарным состояниям атома соответствуют стационарные орбиты, по которым вращаются электроны. При движении по стационарным орбитам электроны, несмотря на наличие у них ускорения, не излучают электромагнитных волн.
Правило квантования орбит Бора: в стационарном состоянии атома электрон, двигаясь по круговой стационарной орбите, может иметь только дискретные (квантованные) значения момента импульса, удовлетворяющие условию Len = pe·rn = me·vn·rn = n ћ,
где n = 1, 2 …, ћ= h/2π, vn – скорость электрона на стационарной орбите радиусом rn.
Это условие может быть
сформулировано в виде условия квантования длины стационарной орбиты электрона:
так как 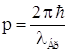 ,
, 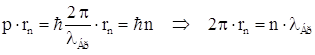 , т.е. на длине стационарной орбиты
электрона должно укладываться целое число длин волн де Бройля.
, т.е. на длине стационарной орбиты
электрона должно укладываться целое число длин волн де Бройля.
Понятие орбиты электрона. С точки зрения квантовой механики орбита электрона – это геометрическое место точек, в которых с наибольшей вероятностью может находиться электрон.
II постулат Бора (правило частот): при переходе атома из одного стационарного состояния в другое испускается или поглощается один фотон с энергией hν = Еn–Еm,
где Еn, Еm – энергии соответствующих стационарных состояний.
Излучение (испускание фотона) происходит при переходе атома из состояния с большей энергией в состояние с меньшей энергией: Еn > Еm . Электрон при этом переходит с более удаленной от ядра орбиты на более близкую.
Поглощение фотона сопровождается переходом атома в состояние с большей энергией: Еn< Еm, электрон переходит на более удаленную от ядра орбиту.
Набор возможных
дискретных частот ![]() квантовых переходов и определяет линейчатость спектров
излучения атомов. Становится ясен физический смысл целых чисел в формулах
Бальмера:
квантовых переходов и определяет линейчатость спектров
излучения атомов. Становится ясен физический смысл целых чисел в формулах
Бальмера: 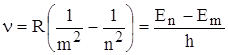 , следовательно,
энергия атома в n – ном стационарном состоянии
, следовательно,
энергия атома в n – ном стационарном состоянии 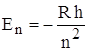 , где n = 1,
2, 3 … Таким образом, целые числа n и m из «сериальных» формул – это квантовые числа, определяющие
дискретные квантованные значения энергии атомов.
, где n = 1,
2, 3 … Таким образом, целые числа n и m из «сериальных» формул – это квантовые числа, определяющие
дискретные квантованные значения энергии атомов.
Водородоподобные системы по Бору.
Водородоподобные системы состоят из ядра с зарядом Z·qe и одного электрона, вращающегося вокруг ядра. Например: атом водорода (при Z = 1); ионизованные атомы He+, Li++ или другие атомы, из которых удалены все электроны, кроме одного.
Для водородоподобных
систем из II -го закона Ньютона движения
электрона по круговой орбите 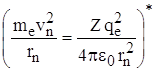 и
правила квантования орбит (me·vn·rn = nћ, т.е.
и
правила квантования орбит (me·vn·rn = nћ, т.е. 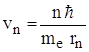 ) можно определить радиус n – ой
орбиты электрона:
) можно определить радиус n – ой
орбиты электрона: 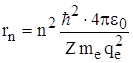 .
.
Для водорода (т.е. Z = 1) для основного состояния (т.е. n = 1) радиус первой орбиты электрона называется Боровским радиусом и обозначается а0:
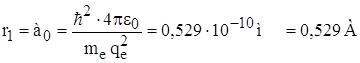 .
.
Вообще, энергетическое состояние с n = 1 называется основным или нормальным (невозбужденным), а все состояния атомов с n > 1 – возбужденными.
Полная энергия электрона
в водородоподобной системе равна сумме кинетической энергии электрона и его потенциальной
энергии в поле ядра: 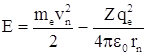 .
.
Так как 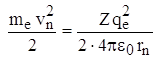 (из *), то
(из *), то 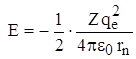 или подставляя
или подставляя 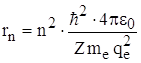 , получаем выражение для энергии электрона в n – ном стационарном состоянии:
, получаем выражение для энергии электрона в n – ном стационарном состоянии:
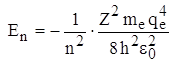 , где n = 1,
2, 3 …
, где n = 1,
2, 3 …
Для атома водорода (Z = 1): 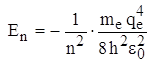 ,
и для основного невозбужденного состояния (n = 1)
,
и для основного невозбужденного состояния (n = 1) 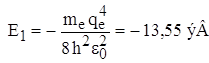 .
.
Из сравнения данного
выражения для Еn и Еn
из формулы Бальмера можно получить постоянную Ридберга: 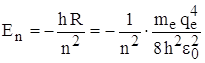 и тогда
и тогда 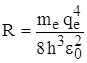 .
.
Физический смысл знака «–» в формуле для энергии электрона (энергия отрицательна) заключается в том, что электрон в атоме под действием силы притяжения к ядру находится в связанном состоянии. |Еn| называется энергией связи (энергией отрыва) электрона в n – ом состоянии; а состояние с n = ∞ соответствует свободному состоянию электрона, т.е. Е∞ = 0.
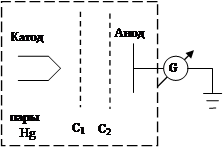
Экспериментальным подтверждением постулатов Бора явились опыты Франка – Герца (1913 г.) по изучению столкновений электронов с атомами газов (в частности, паров ртути) методом задерживающего потенциала.
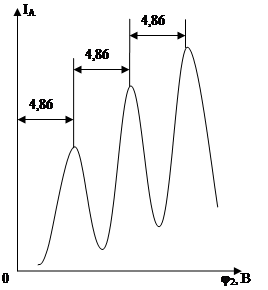
Вылетающие с термокатода К и ускоренные сетками С1 и С2 электроны испытывали столкновения с атомами паров ртути (давление в запаянной трубке составляло ~ 1 мм рт. ст.). Это были как упругие соударения, при которых изменялось только направление движения электронов, а энергия оставалась неизменной, так и неупругие соударения, при которых часть энергии электронов передавалась атомам ртути. При этом согласно I–ому постулату Бора, атом ртути может принять не любое количество энергии, а только определенную энергию для перехода из одного стационарного состояния в другое. Ближайшее к основному невозбужденному состояние отстоит от него на 4,86 эВ. Действительно, при Ее< 4,86 эВ наблюдались только упругие соударения, при которых электроны не теряли свою энергию, и электронный ток на аноде IA увеличивался в ростом потенциала на второй сетке С2. Когда энергия, накапливаемая электронами в пространстве между катодом и сетками, достигала значения Ее = 4,86 эВ начинались неупругие соударения. Энергия электронов уменьшалась, ее оказывалось уже недостаточно для преодоления потенциала задержки φзадерж между сеткой С2 и анодом А, и ток IA резко уменьшался. Аналогичный спад тока IA наблюдался и при φ2 = 2·4,86; 3·4,86 … и т.д., когда электроны испытывали 2, 3 … неупругих соударения с атомами ртути.
Эксперименты Франка – Герца подтвердили и второй постулат Бора. Атомы ртути, перешедшие из-за столкновений с электронами в возбужденные состояния, испускали УФ излучение, что соответствовало длине волны λ = с/ν = с·h/(Е2 – Е1) = 255 нм.
Недостатки теории Бора:
1. Внутренняя противоречивость, непоследовательность (соединение классической физики и квантово-механических постулатов).
2. Никак не объяснялось различие интенсивностей спектральных линий излучения, т.е. не было объяснения тому, что некоторые энергетические переходы оказываются более вероятными, чем другие.
3. Не позволяла создать теоретические модели более сложных атомных систем, например, гелия всего с двумя электронами в атоме.
Теория Бора была заменена последовательной квантовой теорией, учитывающей волновые свойства микрочастиц, получившей название квантовая (волновая) механика.
Стационарное уравнение Шредингера для атома водорода.
Рассмотрим систему,
состоящую из неподвижного ядра с положительным зарядом Z·qe и
одного электрона, вращающегося вокруг ядра. Потенциальная энергия
взаимодействия между ними 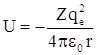 .
Силовое поле, в котором движется электрон, является центрально–симметричным
(потенциальная ловушка гиперболического вида), поэтому целесообразно
использовать сферическую систему координат, где r – радиус-вектор, θ – полярный угол, φ – азимутальный угол. Переход от
декартовой системы координат к сферической осуществляется по следующим
формулам:
.
Силовое поле, в котором движется электрон, является центрально–симметричным
(потенциальная ловушка гиперболического вида), поэтому целесообразно
использовать сферическую систему координат, где r – радиус-вектор, θ – полярный угол, φ – азимутальный угол. Переход от
декартовой системы координат к сферической осуществляется по следующим
формулам: ![]() .
.
Легко проверить, что
тогда выполняется соотношение ![]() .
.
Оператор Лапласа 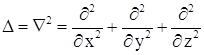 в сферических координатах имеет
вид
в сферических координатах имеет
вид
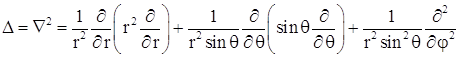
Стационарное уравнение
Шредингера ![]() для
рассматриваемой задачи можно записать как
для
рассматриваемой задачи можно записать как 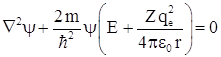 , или в сферических координатах
, или в сферических координатах
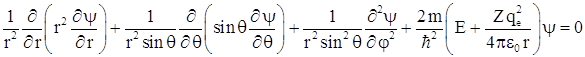
Для решения
дифференциальных уравнений такого типа используется метод разделения
переменных, поэтому решение ищется в виде ![]() или, совмещая функции угловых координат
или, совмещая функции угловых координат ![]() . При дифференцировании по r функция
. При дифференцировании по r функция ![]() считается постоянной, при дифференцировании по
угловым координатам θ и φ функция R(r) – также постоянной.
считается постоянной, при дифференцировании по
угловым координатам θ и φ функция R(r) – также постоянной.
После подстановки ![]() в уравнение получаем
в уравнение получаем
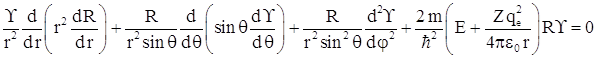
Умножим обе части
уравнения на ![]() и проведем
разделение переменных, тогда
и проведем
разделение переменных, тогда
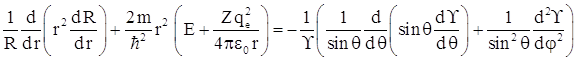
В левую часть уравнения
входят величины, зависящие только от r, а в правой части – величины, зависящие только от угловых координат θ и φ. Такое
возможно только в том случае, если обе части уравнения равны некоторой
постоянной величине, которую называют постоянной разделения. Пусть эта
постоянная разделения равна l (l +1), где l –
целые числа. Итак, для левой части уравнения получаем 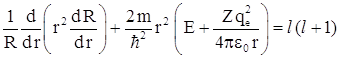 или
или
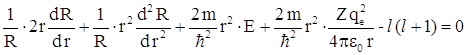
После умножения уравнения
на ![]() получаем:
получаем:
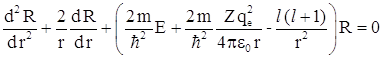
Введем безразмерную
переменную 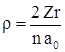 и безразмерный
энергетический параметр
и безразмерный
энергетический параметр 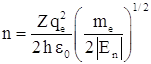 . Здесь
. Здесь
![]() – боровский радиус
– боровский радиус 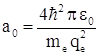 , а n совпадает с величиной n, выраженной из ранее полученного выражения для энергии
электрона в n – ном стационарном состоянии
, а n совпадает с величиной n, выраженной из ранее полученного выражения для энергии
электрона в n – ном стационарном состоянии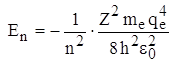 .
.
Тогда решение последнего
уравнения для R(r)
получается в виде ![]() , где
, где ![]() – присоединенные полиномы
Лагерра порядка р и степени m, причем
– присоединенные полиномы
Лагерра порядка р и степени m, причем ![]() .
Таким образом, функция R(r) оказывается функцией двух целых чисел n и l.
.
Таким образом, функция R(r) оказывается функцией двух целых чисел n и l.
Угловая часть волновой
функции также ищется с помощью разделения переменных (θ и φ) и имеет
вид ![]() , где
, где ![]() – полиномы Лежандра от аргумента
– полиномы Лежандра от аргумента ![]() , а число m принимает следующие значения
, а число m принимает следующие значения ![]() . Функция угловых координат
. Функция угловых координат ![]() определяется целыми числами l и m.
определяется целыми числами l и m.
Полная координатная часть
волновой функции, являющейся решением уравнения Шредингера, имеет вид ![]() .
.
Для основного
невозбужденного состояния (при n = 1,
l = 0, m = 0)
угловая часть ![]() , и волновая
функция записывается в виде
, и волновая
функция записывается в виде ![]() .
.
Постоянная С определяется из условия нормировки вероятности на единицу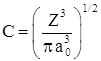 .
.
Для атома водорода (Z = 1) в основном энергетическом состоянии (1S – состояние с n = 1,
l = 0, m = 0)
можно записать ![]() .
.
Определим для этого
случая постоянную С. Условие нормировки вероятности на
единицу имеет вид 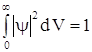 .
Подставляя выражение для
.
Подставляя выражение для ![]() с
учетом того, что
с
учетом того, что ![]() , получаем
, получаем
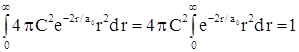 .
.
Воспользовавшись
соотношением 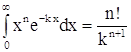 (для нашего
случая
(для нашего
случая 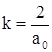 и
и ![]() ), получаем
), получаем 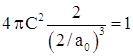 или
или ![]() и окончательно
и окончательно 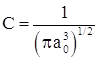 .
.
Тогда нормированная
волновая функция 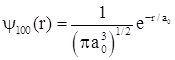 .
.
Собственные значения уравнения Шредингера, определяющие энергию электрона в атоме, совпадают с полученными ранее по теории Бора:
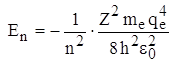 или
или 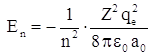 где n = 1, 2, 3 …
где n = 1, 2, 3 …
Таким образом, энергетические уровни стационарных состояний электрона определяются только главным квантовым числом n.
Каждому значению n соответствует l = 0, 1 ,2 …(n – 1), всего n значений,
каждому значению l соответствует m = 0,
±1, ±2, …. ± l, всего (2l + 1)
значений. Следовательно, каждому значению n соответствует ![]() возможных ψ – функций, т.е. кратность
вырождения энергетических уровней равна n2.
возможных ψ – функций, т.е. кратность
вырождения энергетических уровней равна n2.
C9-4
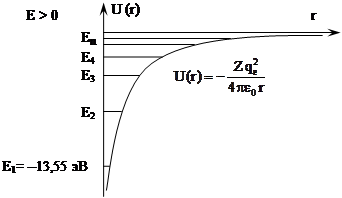
Значение квантовых чисел как следствие стационарного уравнения Шредингера:
n – главное квантовое число, определяющее энергетические уровни электрона в атоме,
n = 1, 2, 3 …
l – орбитальное (азимутальное) квантовое число, определяющее момент импульса электрона в атоме (механический орбитальный момент), l = 0, 1, 2, … (n – 1).
Одним из важнейших
следствий уравнения Шредингера является квантование орбитального момента
импульса электрона: ![]() ,
,
т.е. модуль орбитального момента может принимать лишь значения, кратные ћ и определяемые орбитальным квантовым числом l.
m – магнитное квантовое число, задающее проекцию момента импульса электрона на направление внешнего магнитного поля, m= 0, ±1, ±2, … ± l.
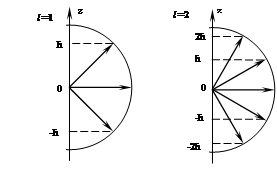
В квантовой механике
существует строгое доказательство того, что вектор ![]() момента импульса электрона может иметь лишь такие
ориентации в пространстве, при которых его проекция Llz на направление внешнего магнитного
поля (OZ) принимает квантованные значения,
кратные ћ и определяемые магнитным квантовым
числом m: Llz =
ћ·m.
момента импульса электрона может иметь лишь такие
ориентации в пространстве, при которых его проекция Llz на направление внешнего магнитного
поля (OZ) принимает квантованные значения,
кратные ћ и определяемые магнитным квантовым
числом m: Llz =
ћ·m.
Это следствие решения уравнения Шредингера для водородоподобных систем называется пространственным квантованием.
Как уже говорилось, понятие орбиты электрона в квантовой механике носит вероятностный характер. Вероятность обнаружения электрона в единичном объеме отличается в различных точках пространства и может
быть определена через волновую
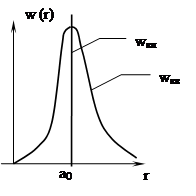
функцию ![]()
По теории Бора вероятность dw ≠ 0 только для r = a0 (для n = 1). При квантово-механическом рассмотрении существует ненулевая вероятность обнаружения электрона в любой точке пространства, но эта вероятность имеет максимальное значение в окрестности r = a0: электрон как бы «размазан» в пространстве, образуя электронное облако, густота (плотность) которого характеризует вероятность нахождения в данной точке. При этом квантовые числа n и l определяют размер и форму электронного облака, а m характеризует ориентацию облака в пространстве.
Описание состояние электронов в атоме. В зависимости от квантовых чисел вводится определенная символика обозначения состояния электрона:
| l = 0 | S - состояние | Shapp (резкая) серия излучения |
| l = 1 | p - состояние | Principal (главная) |
| l = 2 | d - состояние | Diffuse (диффузная) |
| l = 3 | f - состояние | Fundamental (основная), |
| и далее по английскому алфавиту (g, h …) |
Значение главного квантового числа n указывается перед орбитальным числом l :
1S (n = 1, l =0, m = 0)
2S (n = 2, l =0, m = 0), 2p (n = 2, l =1, m= ±1)
3S (n = 3, l =0, m = 0), 3p (n = 3, l =1, m= ±1), 3d (n = 3, l =2, m= ±2) и т.д.
Испускание (поглощение) излучения атомами происходит только при переходах атома с одного энергетического уровня на другой, подчиняющихся правилам отбора – правилам, ограничивающим число возможных переходов, связанных с испусканием (поглощением) энергии.
Правила отбора для орбитального квантового числа l : возможны только такие переходы, при которых изменение l подчиняется соотношению Δ l = ± 1.
Это правило отбора непосредственно следует из закона сохранения момента импульса: так как фотон обладает собственным моментом импульса (≈ ћ), то при поглощении фотона атом получает дополнительный момент ћ, а при испускании его момент импульса соответственно уменьшается на эту величину.
Правила отбора для магнитного квантового числа m: возможны только такие переходы, при которых изменение m подчиняется соотношению Δ m = 0, ± 1.
Спектр излучения атомов
Ширина спектральных линий
Из возбужденного
состояния атом может спонтанно перейти в состояние с более низким значением
энергии. Время существования атома в возбужденном состоянии (время жизни
возбужденного состояния) τ
~ 10-9 с,
т.е. некоторая конечная величина. Поэтому в соответствии с принципом
неопределенностей Гейзенберга энергия возбужденного состояния не может быть
определена с любой степенью точности и имеет некоторый разброс значений ΔЕ.
Следовательно энергия испускаемых при таком переходе фотонов будет лежать в
некотором диапазоне ΔЕ, и при этом ΔЕ·τ ≥ ћ. Соответственно, спектральная линия излучения расширяется ![]() . Здесь
. Здесь ![]() – ширина спектральной линии излучения – разность
частот, которые соответствуют ½
максимальной интенсивности излучения I (фактически
это «ширина на полувысоте»).
– ширина спектральной линии излучения – разность
частот, которые соответствуют ½
максимальной интенсивности излучения I (фактически
это «ширина на полувысоте»).
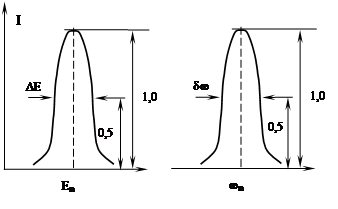
Длина волны излучения
также превращается в некоторый диапазон. Так как ![]() ,
, 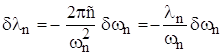 .
.
Величины ![]() и
и ![]() называют естественной шириной спектральных линий,
их обычные значения составляют:
называют естественной шириной спектральных линий,
их обычные значения составляют: ![]() = 108 рад/с,
= 108 рад/с, ![]() = 10-14 м.
= 10-14 м.
Кроме естественного
уширения существует также доплеровское уширение спектральных линий излучения
атомов. Эффектом Доплера называют изменение частоты излучения вследствие
движения источника и/или приемника волн излучения. В применении к излучению
атомов доплеровское уширение спектральных линий возникает из-за теплового
движения излучающих атомов. При этом ![]() , где v –
средняя скорость теплового движения атомов,
, где v –
средняя скорость теплового движения атомов, ![]() = (Em – En)/ћ – частота излучения при переходе атома с
энергетического уровня Em на
уровень En. Видно, что
= (Em – En)/ћ – частота излучения при переходе атома с
энергетического уровня Em на
уровень En. Видно, что 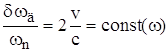 , т.е. относительное доплеровское уширение
не зависит от частоты излучения. Для длины волны излучения имеем: так как
, т.е. относительное доплеровское уширение
не зависит от частоты излучения. Для длины волны излучения имеем: так как 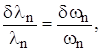
![]() , и при обычных значениях тепловой скорости v ≈
103 м/с доплеровское уширение
, и при обычных значениях тепловой скорости v ≈
103 м/с доплеровское уширение ![]() 10-12 м.
10-12 м.
Действительная ширина
спектральных линий складывается из естественной и доплеровской величин ![]() .
.
Таким образом, при излучении атомами максимум интенсивности излучения смещается в область меньших частот ω (больших длин волн λ), а при поглощении излучения – область больших ω (меньших λ).