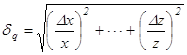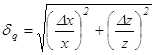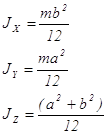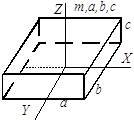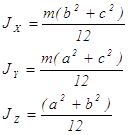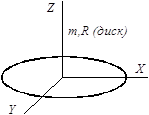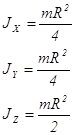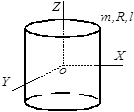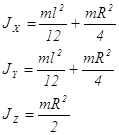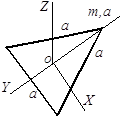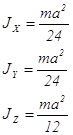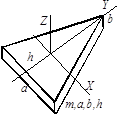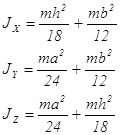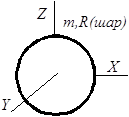Учебное пособие: Кинематика и динамика поступательного движения
Общий физический практикум
Часть I
МЕХАНИКА
ОГЛАВЛЕНИЕ
Указания к выполнению лабораторных работ по механике ………......4
Математическая обработка результатов измерений ................................6
Лабораторная работа №1. Изучение кинематики и динамики поступательного движения на машине Атвуда ...........................................................13
Лабораторная работа №2. Изучение вращательного движения твердого тела ........................................................................................................…........ 17
Лабораторная работа №3. Определение момента инерции и проверка теоремы Гюйгенса – Штейнера методом крутильных колебаний.
Трифлярный подвес ....................................................................…................ 21
Лабораторная работа №4. Определение момента инерции махового колеса и момента силы трения в опоре ............……………………………… 26
Лабораторная работа №5. Изучение законов сохранения энергии и импульса при ударе………..……………………………………….....................29
Лабораторная работа №6. Определение скорости полета пули методом баллистического маятника ...................………………….............................. 34
Лабораторная работа №7. Изучение физического маятника....……........37
Лабораторная работа №8. Изучение колебательного движения с помощью математического маятника..................................................................... 40
Лабораторная работа №9. Определение ускорения свободного падения при помощи оборотного маятника ....................................…........................ 44
Лабораторная работа №10. Изучение сложения колебаний с помощью электронного осциллографа ..................………………................................. 46
Лабораторная работа №11. Исследование собственных колебаний струны методом резонанса ......................................................................................55
Лабораторная работа №12. Определение скорости звука в воздухе .......58
Лабораторная работа №13. Определение модуля сдвига методом крутильных колебаний ...........................................................................................60
Лабораторная работа №14. Изучение деформации растяжения ............. 64
Приложение 1. Формулы для вычисления погрешностей ..........................70
Приложение 2. Моменты инерции твердых тел, имеющих простую геометрическую форму .........................................................................................71
Приложение 3. Упругие характеристики некоторых металлов и сплавов…………..................................................................................................... 72
УКАЗАНИЯ К ВЫПОЛНЕНИЮ ЛАБОРАТОРНЫХ
РАБОТ ПО МЕХАНИКЕ
Глубокое усвоение физики вообще и механики в частности возможно путем изучения теории и в процессе ее применения для решения различных расчетных, качественных и экспериментальных задач.
С физическим экспериментом студент знакомится уже на лекционных занятиях по физике. Но приобщение его к экспериментальным методам и приемам начинается с лабораторного практикума по механике в курсе «Физические лаборатории». Здесь применяются и теория, и, кроме того, формируются практические умения и навыки в проведении физических измерений, в обработке и представлении результатов.
Перечень работ, предлагаемых в данном Практикуме, предназначен для студентов- физиков и отвечает требованиям, предъявляемым к этому виду занятий, и имеет резерв работ и заданий к некоторым из них. Это позволяет использовать его при постановке практикума по физике для студентов других специальностей.
Практикум по механике содержит инструкции и методические указания к выполнению работ, построенных единообразно, по примерной форме: цель работы, идея эксперимента, теория, экспериментальная установка, проведение эксперимента. В заданиях к работе подробно описана методика эксперимента и даны указания к обработке результатов.
Качественное выполнение и успешная защита результатов лабораторных работ студентами невозможны без самостоятельной предварительной подготовки к лабораторным занятиям. В процессе подготовки к очередному занятию, прежде всего, необходимо изучить по данному руководству описание выполняемой работы. Однако, ограничиться только этим нельзя, так как теоретическое введение к каждой работе, приведенное в данном пособии, не может рассматриваться как достаточный минимум для глубокого понимания физических основ работы. Поэтому необходимо к каждой работе читать материал, соответствующий теме работы, по учебнику. Нельзя приступать к работе без усвоения ее основных теоретических положений, не осознав логики процедуры измерений, не умея пользоваться измерительными приборами, относящимся к этой работе. Приступая к работе, студент должен твердо представлять цель данной работы, общий план работы, т.е. последовательность действий при проведении измерений. Это является главным основанием для допуска к работе при собеседовании с преподавателем в начале занятия.
Приступая к выполнению лабораторной работы, студент должен осуществить сборку и настройку установки, соблюдая при этом указания настоящего руководства и правила техники безопасности. Тщательность в подготовке приборов к измерениям и в проведении самих измерении является залогом хороших окончательных результатов. Правильность сборки проверяется преподавателем или лаборантом, после чего студент получает разрешения приступить к работе.
Результаты измерений должны быть оформлены в виде краткого отчета. В учебной лаборатории имеются примерные формы отчетов по каждой работе. В них показано, какие именно таблицы, графики, расчеты обязательны в отчетах. Отчеты должны содержать выводы, сделанные на основании результатов работы. Если есть необходимость, студент имеет право корректировать форму отчета, добиваясь максимальной на-
глядности представления результатов. При обработке результатов измерений следует уделять большое внимание расчету погрешностей измерений и критическому анализу полученных результатов, который должен быть представлен в выводах.
Наличие отчетов и их защита являются основанием для зачета каждой работы и зачета по курсу «Физические лаборатории».
Рекомендуемая литература
Теория
1. Александров Н.В., Яшкин Л.Я. Курс общей физики. Механика. - М.: Просвещение, 1978.
2. Архангельский М.М. Курс физики. Механика. - М.: Просвещение, 1975.
3. Детлаф А.А., Яворский Б.М. Курс физики, т. I. - М.: Высшая школа, 1973.
4. Савельев И.В. Курс общей физики. Механика и молекулярная физика. - М.: Наука, 1986.
5. Савельев И.В. Курс физики, т. I. - М.: Наука, 1973.
6. Сивухин Д.В. Общий курс физики, т. I. - М.: Наука, 1975.
7. Стрелков С.П. Механика. - М.: Наука, 1975.
8. Хайкин С.Э. Физические основы механики. - М.: Наука, 1971.
9. Фриш С.Э., Тиморева А.В. Курс общей физики, т. I. - М.: Физматгиз, 1961.
Физические лаборатории
1. Александров Н.В. Практикум по общему курсу физики. Механика и акустика. М.: Просвещение, 1964.
2. Каленков С.Г., Соломахо Г.И. Практикум по физике. Механика. – М: Высшая школа, 1990.
3. Кортнев А.В., Рублев Ю.В., Куценко А.Н. Практикум по физике. – М.: Высшая школа, 1965.
4. Лабораторный практику по общей физики. / Под. ред. Гершензона и Малова Е.М. - М.: Просвещение, 1985.
5. Руководство к лабораторным занятиям по физики. / Под. ред. Гольдена Л.Л. - М.: Наука, 1964.
6. Салецкий А.М., Слепков А.И. Динамика твердого тела. Лабораторный практикум. – М.: издательство физического факультета МГУ им. М. В. Ломоносова, 1997.
7. Физический практикум, ч. I / Под. ред. Ромченко И.С. – М.: издательство Московского инженерно-физического института, 1970.
8. Физический практикум./ Под. ред. Ивероновой В.И. - М.: Наука, 1967.
МАТЕМАТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ
ИЗМЕРЕНИЙ
Под измерением понимают сравнение измеряемой величины с другой величиной, принятой за единицу измерения.
Измерения подразделяются на прямые и косвенные.
При прямых измерениях определяемую величину сравнивают с единицей измерения непосредственно или при помощи измерительного прибора, проградуированного в соответствующих единицах.
При косвенных измерениях искомая величина определяется (вычисляется) по результатам прямых измерений других величин, которые связаны с измеряемой величиной определенной функциональной зависимостью.
1. Погрешности результатов измерений
Истинное значение физической величины обычно точно определить нельзя. Корректный способ представления результатов любого измерения состоит в том, что экспериментатор указывает свою наилучшую оценку измеряемой величины xнаил и интервал, в котором, как он уверен, она лежит:
(измеренная
величина)![]() (1)
(1)
Например: g=9,82±0,02м/с2.
Величину Dх называют абсолютной погрешностью или доверительным интервалом определения х.
В студенческой лаборатории полученные абсолютные погрешности обычно должны округляться до одной значащей цифры, например Dg=0,02385м/с2»0,02м/с2.. Но, пожалуй, не стоит делать округление типа 0,14»0,1, ведь это сразу на 40% уменьшает погрешность.
Запись результата измерения в виде (1) необходимо делать так, чтобы последняя значащая цифра должна быть того же порядка (находиться в той же десятичной позиции), что и погрешность. Например: 92,8±0,3; 93±3; 90±30.
Очевидно, что качество измерения характеризуется не только самой абсолютной погрешностью, но также и отношением Dx к xнаил, т.е. относительной погрешностью измерения
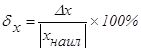 .
(2)
.
(2)
По-видимому, простейший тип учебного эксперимента - измерение величины, принятое значение которой известно. Например, эксперимент по определению скорости звука в воздухе обычно завершается сравнением измеренного значения скорости (допустим, 329±5м/с) с принятым (табличным) значением 331м/с. Очевидно, что вывод в данном случае может быть таким: «Измеренное значение скорости звука совпадает с табличным значением с точностью до погрешности измерения». Измерение может рассматриваться как удовлетворительное, даже если принятое значение слегка выходит за рамки измеренного интервала (допустим, 325±5м/с).
Во многих экспериментах измеряют два значения, которые, согласно теории должны быть равны. Две величины считаются равными, если их измеренные интервалы перекрываются. Например, импульсы р1 = 1,51±0,04 кг×м/с и р2= 1,56±0,06 кг×м/с можно
считать «равными с точностью до погрешностей измерений».
Все погрешности подразделяют на систематические, случайные и промахи.
Систематической называют такую погрешность, которая остается постоянной или закономерно изменяется при повторных измерениях одной и той же величины. Такие погрешности возникают в результате конструктивных особенностей измерительных приборов, неточности метода исследования, каких-либо упрощений экспериментатора, применении для вычислений неточных формул, округления констант. Систематические погрешности либо увеличивают, либо уменьшают результаты измерений. В любом измерительном приборе заложена та или иная систематическая погрешность, которую невозможно устранить, но которую можно учесть.
Случайные погрешности – ошибки, появление которых не может быть предупреждено, а их величина непредсказуема. Поэтому случайные погрешности могут оказать определенное влияние на отдельное измерение, но при многократных измерениях они подчиняются статистическим законам и их влияние на результаты измерений можно учесть или значительно уменьшить.
Промахи и грубые погрешности, – чрезвычайно большие ошибки, явно искажающие результаты измерения. Этот класс погрешностей вызван чаще всего неправильными действиями наблюдателя. Измерения, содержащие промахи, следует отбросить.
Для оценки полной погрешности необходимо знать и случайную и систематическую погрешности.
2. Оценка точности результатов одного прямого измерения
Если при повторении измерений в одних и тех же условиях 3 – 4 раза получено одно и то же значение, то это означает, что измерения не обнаруживают случайных изменений, а погрешность обусловлена только систематической погрешностью. Систематическая погрешность в данном случае определяется погрешностями измерительных приборов и часто называется инструментальной или приборной погрешностью. Есть несколько способов задания этой погрешности:
а) Для некоторых приборов инструментальная погрешность дается в виде абсолютной погрешности. Например, для штангенциркуля, в зависимости от конструкции его нониуса,– 0,1 мм или 0,05 мм, для микрометра – 0,01 мм.
б) Для характеристики большинства измерительных приборов часто используют понятие приведенной погрешности dп (класса точности).
Приведенная погрешность – это отношение абсолютной погрешности Dх к предельному значению хпр измеряемой величины (т.е. к наибольшему её значению, которое может быть измерено по шкале прибора). Приведенная погрешность обычно дается в процентах:
![]() .
(3)
.
(3)
По величине приведенной погрешности приборы разделяют на семь классов: 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4.
Зная класс прибора, можно рассчитать его абсолютную погрешность. Например, вольтметр имеет шкалу делений в пределах от 0 до 300 В (хпр=300 В) и класс точности 0,5. Тогда
![]() .
.
в) В некоторых случаях используется смешанный способ задания инструментальной погрешности. Например, весы технические (Т–200) имеют класс точности 2. В то же время указывается, что при нагрузке до 20 г абсолютная погрешность равна 5 мг, до 100 г – 50 мг, до 200 г – 100 мг. Набор школьных гирь относится 4-му классу точности, а допустимые погрешности масс гирь указаны в таблице 1.
Таблица 1
|
Номинальное значение, г |
100 |
50 |
20 |
10 |
5 |
2 |
1 |
|
Абсолютная погрешность, мг |
+40 |
+30 |
+20 |
+12 |
+8 |
+6 |
+4 |
|
Номинальное значение, г |
500 |
200 |
100 |
50 |
20 |
10 |
5 |
|
Абсолютная погрешность, мг |
±3 |
±2 |
±1 |
±1 |
±1 |
±1 |
±1 |
Если, например, при взвешивании на таких весах с таким набором гирь получено значение массы тела 170 г (100 г + 50 г + 20 г), то абсолютная погрешность взвешивания равна: Dх = 40 + 30 + 20 + 100 = 200 (мг)=0,2(г).
г) В тех случаях, когда класс точности прибора не указан, абсолютная погрешность принимается равной половине цены наименьшего деления шкалы прибора. Так при измерении линейкой, наименьшее деление которой 1 мм, абсолютная погрешность равна 0,5 мм.
3. Статистический анализ случайных погрешностей
Пусть при повторении измерений одной и той же физической величины х в одинаковых условиях получены различные значения: x1, x2, …, xn. Это означает, что есть причины, приводящие к случайному «разбросу» измеряемой величины xi (помехи, трение и т. п.). В этом случае наилучшей оценкой измеряемой величины является среднее арифметическое значение найденных значений xi
![]() ,
(4)
,
(4)
где n - число измерений.
 При наличии случайных погрешностей появление того
или иного значения величины xi является
случайным событием. Вероятность появления того или иного значения чаще всего
определяется законом нормального распределения Гаусса. Распределение
случайных погрешностей также чаще всего бывает нормальным. Поэтому
распределение Гаусса может быть записано и как закон нормального
распределения случайных погрешностей
При наличии случайных погрешностей появление того
или иного значения величины xi является
случайным событием. Вероятность появления того или иного значения чаще всего
определяется законом нормального распределения Гаусса. Распределение
случайных погрешностей также чаще всего бывает нормальным. Поэтому
распределение Гаусса может быть записано и как закон нормального
распределения случайных погрешностей ![]() ,
которое при бесконечно большом числе измерений имеет вид:
,
которое при бесконечно большом числе измерений имеет вид:
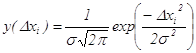 .
(5)
.
(5)
Наилучшей оценкой погрешности отдельного измерения в этом случае является стандартное отклонение (СО):
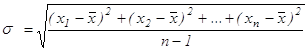 .
(6)
.
(6)
Величину s2 называют дисперсией.
На кривой нормального распределения случайных погрешностей
(рис. 1) имеются две характерные точки перегиба А, А. Абсциссы этих
точек равны ±s, т. е. стандартному отклонению. Можно показать, что вероятность
появления погрешностей, не выходящих за пределы ±s, равна 0,6827 (» 68 %) . Иначе говоря, при достаточно
большом числе измерений (практически при n³30) приблизительно 70 % результатов
измерений будут попадать в интервал ![]() .
В другой терминологии: «попадание результата
.
В другой терминологии: «попадание результата
измерений в доверительный интервал ![]() гарантировано с
надежностью a = 0,68»
гарантировано с
надежностью a = 0,68»
Конечно, надёжность измерений может быть задана и большая, чем 0,68. В этом случае доверительный интервал расширяется и его границы могут быть рассчитаны с помощью так называемых коэффициентов Стьюдента. При выполнении учебных лабораторных работ вполне можно ограничиться надежностью a =0,68.
Стандартное отклонение характеризует среднюю
погрешность отдельных измерений. Результат измерений ![]() есть
разумная комбинация всех n измерений, и поэтому имеются основания полагать, что он будет более надёжным,
чем любое из отдельных измерений.
есть
разумная комбинация всех n измерений, и поэтому имеются основания полагать, что он будет более надёжным,
чем любое из отдельных измерений.
Стандартное отклонение среднего (СОС или SDOM - standard deviation of the mean) равно стандартному отклонению s, деленному на ![]() :
:
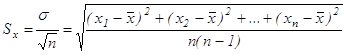 .
(7)
.
(7)
Таким образом, результат многократных измерений какой-либо физической величины должен представляться в виде:
![]() .
(8)
.
(8)
Чтобы учесть и случайную и систематическую погрешность, т.е. рассчитать полную погрешность измерений, обычно используют правило квадратичного сложения:
![]() .
(9)
.
(9)
4. Оценка точности косвенных измерений
Большинство физических величин обычно невозможно измерить непосредственно, и их определение включает два различных этапа. Сначала измеряют одну или более величин x,...,z, которые могут быть непосредственно измерены и, с помощью которых можно вычислить интересующую нас величину. Затем, используя измеренные значения x,..., z, вычисляют саму искомую величину. Если измерение включает эти два этапа, то и оценка погрешностей тоже включает их. Сначала надо оценить погрешности в величинах, которые измеряются непосредственно, а затем определить, к какой погрешности они приводят в конечном результате. При этом, конечно, необходимо учитывать вид функциональной связи между величинами.
Погрешность функции q=f(x,...,z) нескольких переменных x,...,z, измеренных с погрешностями Dx,...,Dz ... в случае, если погрешности независимы и случайны, определяется по формуле:
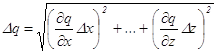 .
(10)
.
(10)
Вычисления погрешности с помощью формулы (9) обычно оказываются достаточно громоздкими. Поэтому лучше производить поэтапное вычисление, используя некоторые правила, два из которых являются наиболее употребляемыми:
1. Абсолютная погрешность суммы и разности равна квадратичной сумме абсолютных погрешностей
![]() .
(11)
.
(11)
2. Относительная погрешность комбинации произведения и частного равна квадратичной сумме относительных погрешностей
![]() ,
,
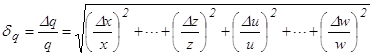 . (12)
. (12)
Правила вычисления погрешностей для некоторых других функций приведены в Приложении 1.
Рассмотрим последовательность действий при вычислении погрешности косвенного измерения на примере формулы
![]() .
.
Сначала найдем абсолютную и относительную погрешность суммы w=m+M:
![]() .
.
Затем найдем относительную и абсолютную погрешности величины v:
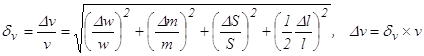 .
.
Анализ полученной окончательной формулы позволяет установить:
а) Погрешности каких именно величин вносят наибольший вклад в общую погрешность. Точному измерению этих величин необходимо уделить наибольшее внимание.
б) Погрешности каких величин практически не влияют на окончательный результат и их можно даже отбросить.
Будем в дальнейшем не принимать в расчет погрешности постоянных (g, e, p ...) и табличных величин, измеренных с большой точностью. Например, погрешность приближенного числа p»3,14 составляет всего 0,05 %.
5. Линеаризация функции и метод наименьших квадратов
 В физических исследованиях
очень часто для сравнения эксперимента с теорией пользуются методом линеаризации
теоретической зависимости, Например, исследуется зависимость перемещения S равноускоренного движения от
времени движения. Теоретическая зависимость имеет вид
В физических исследованиях
очень часто для сравнения эксперимента с теорией пользуются методом линеаризации
теоретической зависимости, Например, исследуется зависимость перемещения S равноускоренного движения от
времени движения. Теоретическая зависимость имеет вид
![]() , (13)
, (13)
где а – ускорение грузов.
Если по экспериментальным точкам построить график зависимости S от t, представляющий собой восходящую кривую, то по виду графика нельзя утверждать, что это парабола и именно та парабола второго прядка, которая соответствует проверяемой закономерности, т. к. похожие графики могут иметь другие закономерности. Единственным графиком, по внешнему виду которого можно однозначно судить о характере исследуемой зависимости, является прямая линия. Для того, чтобы воспользоваться этим свойством
в проверяемой закономерности необходимо выявить в ней такие новые переменные, зависимость между которыми была бы линейной. В нашем случае такими переменными являются S и t2. Следовательно, для проверки справедливости соотношения (13) имеет смысл строить график экспериментальной зависимости S от t2. На систему координат S, t2 (рис. 2) следует нанести экспериментальные точки, а также вправо и влево от них отложить отрезки, длина которых равна погрешностям измерения t2 (доверительным интервалам). Если через начало координат и доверительные интервалы можно провести прямую линию, т. е. экспериментальная зависимость S = f(t2) является линейной, значит соотношение (13) подтверждено экспериментально.
Используя график линеаризованной зависимости, можно определить некоторые параметры изучаемого явления из следующих соображений. Уравнение прямой можно записать в виде
y = kx +b. (14)
Угловой коэффициент k:
![]() ,
(15)
,
(15)
где Dx – произвольный отрезок на оси 0Х - приращение аргумента, Dy – соответствующее приращение функции. Величина b может быть определена как величина отрезка, отсекаемого графиком на оси 0Y. В нашем случае знание коэффициента k позволяет определить ускорение движения: a = 2k.
При нахождении величин k и b из графика к погрешностям измерения добавляется погрешность построения графика. Существует точный метод нахождения величин k и b – метод наименьших квадратов (МНК). Этот метод позволяет провести прямую так, что сумма квадратов отклонений экспериментальных точек от графика минимальна. Формулы для определения величин k и b имеют вид:
![]() ,
, ![]() .
(16)
.
(16)
Зная k и b и задавшись какими-либо значениями x1 и x2, можно по формуле (14) вычислить y1 и y2. Затем через две точки с координатами (x1,y1) и (x2,y2) проводится искомая линия.
Теория позволяет также найти погрешности коэффициентов k и b. Сначала вычисляют величины:
![]() ,
,![]() .
(17)
.
(17)
Затем вычисляют коэффициент линейной корреляции:
![]() . (18)
. (18)
Это число принимает значения между -1 и +1. Если r близко к ±1, то точки лежат вблизи некоторой прямой линии; если r близко к 0, то точки не коррелированны и либо незначительно, либо совсем не группируются около прямой линии.
Вычисление абсолютных погрешностей коэффициентов k и b выполняется по формулам:
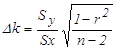 ,
, ![]() . (19)
. (19)
6. Микрокалькулятор
Основным назначением микрокалькулятора является быстрое и точное получение результатов арифметических вычислений. Поэтому отпадает необходимость в применении предварительного округления чисел.
Учитывая, что в лабораторных работах редко встречаются числа, имеющие больше четырех значащих цифр, точность до восьми цифр, получаемых на микрокалькуляторе, является излишней и маскирует существование инструментальной погрешности и по Для того чтобы избежать иллюзорного впечатления о высокой точности результата, полученного с помощью микрокалькулятора, нужно посредством правил подсчета значащих цифр округлить результат математических вычислений так, чтобы точность их соответствовала точности данных, полученных от измерения.
ИЗУЧЕНИЕ КИНЕМАТИКИ И ДИНАМИКИ ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ НА МАШИНЕ АТВУДА
Цель работы
Экспериментальная проверка основных уравнений и законов поступательного движения тела на специально сконструированной для этого лабораторной установке – машине Атвуда.
Идея эксперимента
Несмотря на то, что основные уравнения кинематики и динамики прямолинейного движения имеют простую форму и не вызывают сомнения, экспериментальная проверка этих соотношений весьма сложна. Трудности возникают в основном по двум причинам. Во-первых, при достаточно больших скоростях движения тел необходимо с большой точностью измерять время их движения. Во-вторых, в любой системе движущихся тел действуют силы трения и сопротивления, которые трудно учесть с достаточной степенью точности.
Определим, например, время падения тела с высоты h = 1,0 м при g равным 9,8 м/с2:
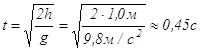 .
(1.1)
.
(1.1)
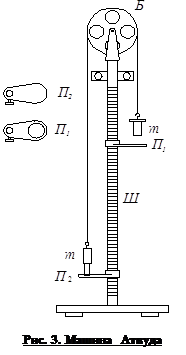 Если при выполнении эксперимента
по определению g по
времени падения тела с указанной высоты допускается погрешность в измерении
времени равная 0,01 с, т. е. возможно получение значений времени 0,46
с или 0,44 с, разброс результатов измерений получается недопустимо
большим: g=9,4 – 10,3 м/с2. С целью уменьшения влияния
точности измерения времени на результаты измерений можно, например, резко
увеличить высоту падения. Но при падении с больших высот достигаются большие
скорости движения, что приводит к резкому увеличению сопротивления воздуха,
которое трудно учесть.
Если при выполнении эксперимента
по определению g по
времени падения тела с указанной высоты допускается погрешность в измерении
времени равная 0,01 с, т. е. возможно получение значений времени 0,46
с или 0,44 с, разброс результатов измерений получается недопустимо
большим: g=9,4 – 10,3 м/с2. С целью уменьшения влияния
точности измерения времени на результаты измерений можно, например, резко
увеличить высоту падения. Но при падении с больших высот достигаются большие
скорости движения, что приводит к резкому увеличению сопротивления воздуха,
которое трудно учесть.
Трудности рассмотренного опыта связаны с большим значением ускорения свободного падения. Так как ускорение большое, то тело быстро набирает скорость, а при этом или время падения мало и его трудно точно измерить, или сама расчетная формула неточна, т. к. не учитывает трение.
Уменьшить ускорение и одновременно максимально уменьшить силу сопротивления можно с помощью устройства, которое называют машиной Атвуда.
Экспериментальная установка
Машина Атвуда (рис. 3) состоит из легкого блока Б, через который переброшена нить с двумя равными грузами на концах (масса обоих грузов одинакова и равна m). Грузы могут двигаться вдоль вертикальной рейки со шкалой Ш. Если на правый груз положить небольшой перегрузок, грузы начнут двигаться с некоторым ускорением. Кольцевая полочка П1, которая может закрепляться в любом положении, предназначена для свободного прохода груза и для снятия перегрузка. Для приема падающего груза служит полочка П2.
Время движения грузов может измеряться с помощью ручного или стационарного се-кундомера.
Машина Атвуда может быть электрифицирована, т. е. снабжена электромагнитной муфтой-пускателем и автоматическим секундомером.
Трение в машине Атвуда сведено к минимуму, но для возможно полной компенсации сил трения масса правого груза делается немного больше массы левого (с помощью дроби или пластилина). Операция балансировки, выполняется с таким расчетом, чтобы грузы не перевешивали друг друга, но от легкого толчка вниз правого груза вся система приходила в равномерное движение. (При расчетах можно считать массы грузов одинаковыми).
 Для выполнения работы машина Атвуда должна быть
установлена строго вертикально, что легко проверить по параллельности шкалы и
нити. Кроме того, в тех опытах, где используется кольцевая полочка, положение
ее должно быть отрегулировано так, чтобы грузы проходили через кольцо не
касаясь его, а перегрузок легко снимался и оставался на полочке.
Для выполнения работы машина Атвуда должна быть
установлена строго вертикально, что легко проверить по параллельности шкалы и
нити. Кроме того, в тех опытах, где используется кольцевая полочка, положение
ее должно быть отрегулировано так, чтобы грузы проходили через кольцо не
касаясь его, а перегрузок легко снимался и оставался на полочке.
Второй закон Ньютона для каждого из тел системы в предположении невесомости блока и отсутствия трения дает
![]()
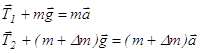 , (1.2)
, (1.2)
где Т1,2 – силы натяжения нити, m – масса каждого груза, Dm – масса перегрузка, а – ускорение системы.
![]() В
проекциях на вертикальную ось ОY получаем соотношения
В
проекциях на вертикальную ось ОY получаем соотношения
![]() (1.3)
(1.3)
Отсюда, так как Т1 = Т2, ускорение движения системы равно
![]() .
(1.4)
.
(1.4)
Из этого выражения видно, во-первых, что ускорение не зависит от времени, что доказывает равноускоренный характер движения грузов. Во-вторых, видно, что изменять ускорение можно, меняя массу перегрузка Dm.
В случае равноускоренного движения скорость грузов v и их перемещение DS за время t определяются уравнениями
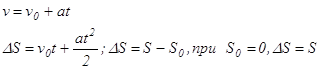 .
(1.5)
.
(1.5)
Так как начальная скорость в опытах на машине Атвуда обычно равна нулю и движение условно начинается из начала координат, то
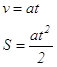 .
(1.6)
.
(1.6)
Будем называть первое из этих соотношений законом скоростей, а второе законом пе-
ремещений.
Соотношения (1.6) могут быть проверены экспериментально.
Проведение эксперимента
Задание 1. Проверка закона скоростей
Измерения
1. Проверяют вертикальность установки машины Атвуда. Балансируют грузы.
2. Укрепляют на шкале кольцевую полочку П1. Регулируют ее положение.
3. Накладывают на правый груз перегрузок в 5-6 г.
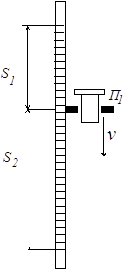 4. Двигаясь равноускоренно
из верхнего положения до кольцевой полочки, правый груз проходит путь S1
за время t1 и приобретает к концу этого движения
скорость v (рис. 5). На кольцевой полочке груз сбрасывает перегрузок и
дальше движется равномерно со скоростью, которую он приобрел в конце
разгона. Для определения ее следует измерить время t2
движения груза на пути S2. Таким образом, каждый опыт состоит
из двух измерений: сначала измеряется время равноускоренного движения t1,
а затем груз повторно запускается для измерения времени равномерного движения t2.
4. Двигаясь равноускоренно
из верхнего положения до кольцевой полочки, правый груз проходит путь S1
за время t1 и приобретает к концу этого движения
скорость v (рис. 5). На кольцевой полочке груз сбрасывает перегрузок и
дальше движется равномерно со скоростью, которую он приобрел в конце
разгона. Для определения ее следует измерить время t2
движения груза на пути S2. Таким образом, каждый опыт состоит
из двух измерений: сначала измеряется время равноускоренного движения t1,
а затем груз повторно запускается для измерения времени равномерного движения t2.
5. Проводят 5-6 опытов при различных значениях пути S1 (с шагом 15-20 см). Путь S2 выбирается произвольно. Полученные данные заносят в таблицу 1.1. отчета
Обработка результатов.
1. По полученным данным строят график зависимости v = f(t). Точку (t=0, v=0) на графике не откладывают.
![]() 2. Если экспериментальные точки
ложатся на прямую с небольшим разбросом и прямая проходит через начало координат,
то можно сделать вывод о выполнении закона скоростей.
2. Если экспериментальные точки
ложатся на прямую с небольшим разбросом и прямая проходит через начало координат,
то можно сделать вывод о выполнении закона скоростей.
3. Для определения с помощью полученного графика ускорения движения сначала необходимо получить точное уравнение экспериментальной прямой. Для этого применяют метод наименьших квадратов (МНК). Угловой коэффициент прямой, т.е. значение коэффициента k в полученном уравнении, равен ускорению а.
4. По формулам МНК определяют погрешность измерения а.
Задание 2. Проверка закона перемещений
1. Снимают с машины кольцевую полочку.
2. На правый груз накладывают перегрузок в 5-6 г.
3. Измеряют время прохождения грузом расстояний в 20, 40, 60 и т.д. см – всего 6-7 опытов. Полученные данные заносят в таблицу 1.2 отчета.
4. Зависимость S = f(t) – квадратичная функция, а ее график – парабола. Однако ее графическая идентификация («узнавание») невозможна. Поэтому строят график зависимости S = f(t2). Точку (t=0, S=0) на графике не откладывают. Если экспериментальные точки ложатся на прямую с небольшим разбросом и прямая проходит через начало координат, то можно сделать вывод о выполнении закона перемещений.
5. Как и в задании 1 для линеаризации зависимости применяют МНК. С помощью полученного уравнения находят ускорение движения и определяют погрешность его измерения.
6. Зная массы грузов и перегрузка, из формулы (1.4) находят ускорение свободного падения. Учитывая погрешности измерения масс грузов и перегрузка, находят относительную и абсолютную погрешность измерения ускорения свободного падения.
Задание 3. Проверка второго закона Ньютона.
Поскольку ускорение движения является функцией двух переменных – силы и массы, то изучение второго закона Ньютона выполняется путем раздельного исследования двух зависимостей: 1) зависимости ускорения от действующей силы при постоянной массе системы и 2) зависимости ускорения от массы системы при постоянной действующей силе.
Исследование зависимости ускорения от силы при постоянной массе
Измерения и обработка результатов
1. Тщательно балансируют грузы, выбрав их массы в пределах 150 - 200 г каждый.
2. Затем на правый груз последовательно накладывают перегрузки. В результате в системе появляется движущая сила равная Dmg, где Dm - суммарная масса перегрузков. При этом, конечно, общая масса системы незначительно увеличивается, но этим изменением массы по сравнению с массой грузов можно пренебречь, считая массу системы постоянной.
3. Измеряют время равноускоренного движения системы на пути, например, 1 метр. Все данные заносят в таблицу 1.3 отчета.
4. Пользуясь законом путей (1.6), вычисляют ускорение а.
5. Поводят еще 5-6 опытов, последовательно увеличивая массу перегрузков.
6. Строят график зависимости ускорения движения от действующей силы. Точку (F=0, a=0) на графике не откладывают. Если экспериментальные точки ложатся на прямую с небольшим разбросом и прямая проходит через начало координат, то можно сделать вывод о том, что ускорение действительно прямо пропорционально силе.
7. По угловому коэффициенту полученной прямой определяют массу системы и сравнивают ее реальной массой.
Исследование зависимости ускорения от массы при постоянной силе
Измерения и обработка результатов
1. Все опыты проводят с одним и тем же перегрузком, т.е. при постоянной действующей силе. Ускорение системы измеряется также как и в предыдущем задании.
2. Для изменения массы системы одновременно на правый и левый груз кладут дополнительные одинаковые грузы. Все данные записывают в таблицу 1.4 отчета.
3. График обратно пропорциональной зависимости ускорения
от массы представляет собой гиперболу, которую невозможно идентифицировать. Для
проверки предположения об обратно пропорциональной зависимости между ускорением
и массой ![]() необходимо построить
график зависимости ускорения от обратного значения массы системы: a = f(М-1). Подтверждением предположения
является прямолинейность этого графика.
необходимо построить
график зависимости ускорения от обратного значения массы системы: a = f(М-1). Подтверждением предположения
является прямолинейность этого графика.
4. По угловому коэффициенту полученной прямой определяют значение приложенной силы и сравнивают ее с реально действующей в системе.
ИЗУЧЕНИЕ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Цель работы
Экспериментальная проверка основного уравнения динамики вращательного движения твердого тела вокруг закрепленной оси.
Идея эксперимента
В эксперименте исследуется вращательное движение закрепленной на оси системы тел, у которой может меняться момент инерции (маятник Обербека). Различные моменты внешних сил создаются грузами, подвешенными на нити, намотанной на шкив.
Теория
Основное уравнение динамики вращательного движения твердого тела с моментом инерции J вокруг неподвижной оси z имеет вид
![]() ,
(2.1)
,
(2.1)
 где
где ![]() -
угловое ускорение, М – полный момент внешних сил. Поскольку величина e является функцией двух переменных,
то изучение закона динамики вращательного движения твердого тела выполняется
путем раздельного исследования двух зависимостей: 1) зависимости углового
ускорения от момента силы при постоянном значении момента инерции (J = const) и 2) зависимости углового ускорения
от момента инерции при постоянном значении момента силы (M = const).
-
угловое ускорение, М – полный момент внешних сил. Поскольку величина e является функцией двух переменных,
то изучение закона динамики вращательного движения твердого тела выполняется
путем раздельного исследования двух зависимостей: 1) зависимости углового
ускорения от момента силы при постоянном значении момента инерции (J = const) и 2) зависимости углового ускорения
от момента инерции при постоянном значении момента силы (M = const).
Полный момент внешних сил равен
M = Mн – Мтр , (2.2)
где Мн – вращающий момент (в данной работе - момент силы натяжения нити) Мтр – момент силы трения. С учетом этого основное уравнение динамики вращательного движения принимает вид линейной зависимости момента силы натяжения Мн от e.
![]() .
(2.3)
.
(2.3)
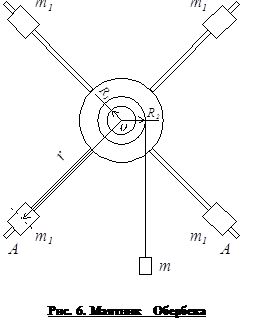
Для экспериментального доказательства справедливости этого соотношения в работе используется маятник Обербека (рис. 6). Он состоит из четырех стержней А и двух шкивов с различными радиусами R1 и R2, укрепленных на одной горизонтальной оси. По стержням могут перемещаться и закрепляться в нужном положении четыре цилиндрических груза (по одному на каждом стержне) одинаковой массы m1. При помощи груза массы m, прикрепленного к концу нити, намотанной на тот или иной шкив, маятник может приводиться во вращение. Определяя продолжительность t движения и перемещение h груза, можно определить ускорение его поступательного движения
![]() . (2.4)
. (2.4)
Это ускорение равно линейному ускорению точек шкива и связано с угловым ускорением крестовины соотношением
![]() .
(2.5)
.
(2.5)
Момент силы натяжения Т нити равен
Mн =ТR . (2.6)
Силу Т можно определить из второго закона Ньютона для поступательного движения, который в проекциях на ось 0Y дает
![]() , (2.7)
, (2.7)
 где m – масса груза.
где m – масса груза.
Таким образом, момент сил натяжения
нити равен
![]() .
(2.8)
.
(2.8)
![]() Согласно (2.3) Мн линейная
функция e. На рис.
7 эти зависимости для различных зна-чений моментов инерции системы изображены в
виде графиков, угловые коэффициенты которых равны J. Эти графики отсекают от оси Мн
отрезки, равные моменту силы трения Мтр. Так как Мтр
одинаков во всех опытах, то все графики должны пересекаться в одной точке.
Функция (2.3) верна для любых двух моментов сил, поэтому
Согласно (2.3) Мн линейная
функция e. На рис.
7 эти зависимости для различных зна-чений моментов инерции системы изображены в
виде графиков, угловые коэффициенты которых равны J. Эти графики отсекают от оси Мн
отрезки, равные моменту силы трения Мтр. Так как Мтр
одинаков во всех опытах, то все графики должны пересекаться в одной точке.
Функция (2.3) верна для любых двух моментов сил, поэтому
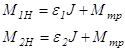 (2.9) Откуда
(2.9) Откуда
![]() .
(2.10)
.
(2.10)
Таким образом, величина J может быть, с одной стороны, измерена, а с другой стороны, рассчитана, исходя из масс и геометрических размеров деталей установки Обербека. Момент инерции J маятника вычисляется из условия аддитивности момента инерции и равен сумме моментов инерции шкивов, крестовины и цилиндрических грузов, вращающихся вокруг оси, не проходящей через их середины. Графики позволяют также определить момент силы трения Мтр., действующей в системе.
Экспериментальная установка
Ось маятника Обербека закреплена в подшипниках, так что вся система может вращаться вокруг горизонтальной оси. Передвигая грузы по спицам, можно легко изменять момент инерции системы. На шкив виток к витку наматывается нить, к которой привязана платформа известной массы. На платформу накладываются грузы из набора. Высота падения грузов измеряется с помощью линейки, укрепленной параллельно нити. Маятник Обербека может быть снабжен электромагнитной муфтой - пускателем и электронным секундомером. Перед каждым опытом маятник следует тщательно отрегулировать. Особое внимание необходимо обратить на симметричность расположения грузов на крестовине. При этом маятник оказывается в состоянии безразличного равновесия.
Проведение эксперимента
Задание 1. Оценка момента силы трения, действующей в системе
Измерения
1. Устанавливают грузы m1 на крестовине в среднее положение, размещая их на равном расстоянии от оси таким образом, чтобы маятник находился в положении безразличного равновесия.
2. Накладывая небольшие грузы на платформу, определяют приближенно минимальную массу m0 , при которой маятник начнет вращаться. Оценивают момент силы трения из соотношения
Мтр = m0gR , (2.11)
где R – радиус шкива, на который намотана нить.
3. Дальнейшие измерения желательно проводить с грузами массой m ³ 10m0.
Задание 2. Проверка основного уравнения динамики вращательного движения
Измерения
1. Укрепляют грузы m1 на минимальном расстоянии от оси вращения. Балансируют маятник. Измеряют расстояние r от оси маятника до центров грузов.
2. Наматывают нить на один из шкивов. По масштабной линейке выбирают начальное положение платформы, производя отсчет, например, по ее нижнему краю. Тогда конечное положение груза будет находиться на уровне поднятой приемной платформы. Высота падения груза h равна разности этих отсчетов и может быть оставлена во всех опытах одинаковой.
3. Кладут на платформу первый груз. Расположив груз на уровне верхнего отсчета, фиксируют это положение, зажимая нить электромагнитной муфтой. Подготавливают к измерению электронный секундомер.
4. Отпускают нить, предоставив грузу возможность падать. Это достигается отключением муфты. При этом автоматически включается секундомер. Удар о приемную платформу останавливает падение груза и останавливает секундомер.
5. Измерение времени падения при одном и том же грузе выполняется не менее трех раз.
6. Проводят измерения времени падения груза m при других значениях момента Мн. Для этого либо добавляют на платформу дополнительные перегрузки, либо перебрасывают нить на другой шкив. При одном и том же значении момента инерции маятника необходимо провести измерения не менее чем с пятью значениями момента Мн .
7. Увеличивают момент инерции маятника. Для этого достаточно симметрично переместить грузы m1 на несколько сантиметров. Шаг такого перемещения должен быть выбран таким образом, чтобы получить 5-6 значений момента инерции маятника. Проводят измерения времени падения груза m (п.2-п.7). Все данные заносят в таблицу 2.1 отчета.
Обработка результатов. Исследование зависимости углового ускорения от момента силы при постоянном значении момента инерции.
1. Пользуясь формулами (2.4.), (2.5), (2.8), определяют для
каждого опыта по средним значениям времени ![]() значения
линейного ускорения а, углового ускорения e и момента силы натяжения нити Мн.
значения
линейного ускорения а, углового ускорения e и момента силы натяжения нити Мн.
2. Строят графики зависимостей момента силы Мн, как функции, от углового ускорения e , как аргумента, для различных моментов инерции маятника J. Т. к. Мн = f(e) – линейная функция, то ее графики будут прямыми линиями. Если экспериментальные точки не ложатся на прямую, графики надо проводить так, чтобы «разброс» точек был приблизительно одинаков по обе стороны прямой. При этом они не обязательно пройдут через одну точку на вертикальной оси. Малый «разброс» точек свидетельствует о хорошей линейности функции Мн = f(e) и том, что угловое ускорение действительно прямо пропорционально полному моменту сил, приложенных к вращающемуся телу.
Обработка результатов. Исследование зависимости углового ускорения от момента инерции при постоянном значении момента силы
1. Для исследования используют ранее построенный график. Рассчитывают моменты инерции маятника по формуле (2.10). Для этого нужно выбирать точки прямо с графиков, например, А(М1н ,e1) и В(М2н,,e2 ).
2. На графике проводят горизонтальную прямую через произвольную точку на оси Мн, пересекающую графики Мн = f(e). Точки пересечения позволяют определить те значения угловых ускорений маятника, которые соответствуют разным значениям моментов инерции, но при постоянном значении момента силы M = Mн – Mтр. Записывают полученные значения e и соответствующие им значения J в таблицу 2.2. отчета.
3. Угловое ускорение обратно пропорционально моменту инерции, т. е. график зависимости e = f(J) представляет собой гиперболу и не идентифицируется. Но график зависимости e = f(J-1) должен представлять собой прямую линию, проходящую через начало координат. Поэтому следует вычислить величины J-1 и построить соответствующий график. Угловой коэффициент наклона этого графика равен полному моменту приложенных сил.
Обработка результатов. Определение момента силы трения, действующей в системе
1. В идеальном случае все графики M=f(e) должны пересекаться в одной точке, лежащей на оси М. Координата этой точки дает значение момента силы трения. Для реальных же графиков, скорее всего, будет иметь место некоторый разброс в положении этой точки.
2. Определить по графику все значения момента силы трения и найти его среднее значение. Сравнить полученный результат с ранее измеренным в задании 1.
Задание 3. Сравнение измеренных и вычисленных значений моментов инерции
маятника
1. Выписывают в таблицу 2.4 отчета измеренные значения моментов инерции маятника.
2. Используя формулы для расчета моментов инерции геометрически правильных тел и теорему Гюйгенса – Штейнера, вычисляют моменты инерции шкивов, крестовины и грузов, вращающихся вокруг оси, не проходящей через их середину. Данные для расчета берут из «паспорта» прибора. Общий момент инерции маятника находится суммированием моментов инерции деталей маятника.
3. Сравнивают вычисленные и измеренные значения моментов
инерции. Находят относительные отклонения вычисленных и измеренных моментов
инерции: ![]() .
.
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ И ПРОВЕРКА ТЕОРЕМЫ ГЮЙГЕНСА-ШТЕЙНЕРА
МЕТОДОМ КРУТИЛЬНЫХ КОЛЕБАНИЙ
Цель работыЭкспериментальная проверка теоремы Гюйгенса – Штейнера и определение моментов инерции тел простой формы.
В эксперименте используется связь между периодом колебаний крутильного маятника и его моментом инерции. В качестве маятника выбрана круглая платформа, подвешенная в поле тяжести на трех длинных нитях (трифилярный подвес). Платформа может совершать крутильные колебания вокруг вертикальной оси. На платформу помещаются тела различной формы, измеряются периоды колебаний маятника и определяются значения моментов инерции этих тел. Теорема Гюйгенса – Штейнера проверяется по соответствию между экспериментальной и теоретической зависимостями моментов инерции грузов от их расстояния до центра платформы.
Теория Основное уравнение
вращательного движения твердого тела вокруг неподвижной оси имеет вид
Основное уравнение
вращательного движения твердого тела вокруг неподвижной оси имеет вид
![]() , (3.1)
, (3.1)
где w - угловая скорость вращения, J – момент инерции тела относительно оси вращения, М – момент внешних сил относительно этой оси.
Теорема Гюйгенса – Штейнера. Если момент инерции тела относительно некоторой оси вращения, проходящей через центр масс, имеет значение J0 , то относительно любой другой оси, находящейся на расстоянии а от первой и параллельной ей, он будет равен
![]() , (3.2)
, (3.2)
где m – масса тела.
Для проверки теоремы Гюйгенса – Штейнера в данной работе исследуются крутильные колебания твердого тела на трифилярном подвесе. Трифилярный подвес представляет собой круглую платформу радиуса R, подвешенную на трех симметрично расположенных нитях одинаковой длины, укрепленных у ее краев (рис. 8). Наверху эти нити также симметрично прикреплены к диску несколько меньшего размера (радиуса r). Платформа может совершать крутильные колебания вокруг вертикальной оси ОО¢, перпендикулярной к ее плоскости и проходящей через ее центр. Такое движение платформы приводит к изменению положения ее центра тяжести по высоте.
Если платформа массы m, вращаясь в одном направлении, поднялась на высоту h, то
приращение ее потенциальной энергии будет равно
![]() ,
(3.3)
,
(3.3)
где g – ускорение силы тяжести. Вращаясь в другом направлении, платформа придет в положение равновесия (h = 0) с кинетической энергией, равной
![]() ,
(3.4)
,
(3.4)
где J – момент инерции платформы, w0 – угловая скорость вращения платформы в момент прохождения ею положения равновесия.
Пренебрегая работой сил трения, на основании закона сохранения механической энергии имеем:
![]() .
(3.5)
.
(3.5)
Считая, что платформа совершает гармонические крутильные колебания, можно записать зависимость углового смещения платформы a от времени t в виде
![]() ,
(3.6)
,
(3.6)
где a - угловое смещение платформы, a0 – угол максимального поворота платформы, т.е. амплитуда углового смещения, Т – период колебания. Для угловой скорости w, являющейся первой производной по времени от величины смещения, можно записать
![]() .
(3.7)
.
(3.7)
В моменты прохождения платформы через положение равновесия (t = 0, 0,5Т, …) величина w(t) будет максимальна и равна
![]() .
(3.8)
.
(3.8)
Из выражений (3.5) и (3.8) следует, что
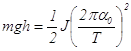 .
(3.9)
.
(3.9)
Если l длина нитей подвеса, R – расстояние от центра платформы до точек крепления нитей на ней, r – радиус верхнего диска (рис. 8), то легко видеть, что
![]() (3.10)
(3.10)
Так как
![]() , (3.11)
, (3.11)
а при максимальном отклонении платформы от положения равновесия
![]() ,
(3.12)
,
(3.12)
то
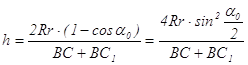 .
(3.13)
.
(3.13)
При малых углах отклонения a0 значение синуса этого угла можно заменить просто значением a0. Учитывая также, что при R<< l величину знаменателя можно положить равной 2l, получаем
![]() (3.14)
(3.14)
При этом закон сохранения энергии (2.9) примет вид:
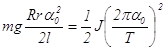 ,
(3.15)
,
(3.15)
откуда следует, что
![]() (3.16)
(3.16)
По формуле (3.16) можно экспериментально определить момент инерции пустой платформы или платформы с телом, положенным на нее, так как все величины в правой части формулы непосредственно измеряются. Следует помнить, что m – это суммарная масса платформы и исследуемого тела, положенного на нее.
Экспериментальная установкаВид установки показан на рис.8. Отношение радиуса платформы к длине нитей подвеса R/l < 0,05, что соответствует приближениям, используемым при выводе формулы (3.16).
Тела на платформу необходимо класть строго симметрично, так, чтобы не было перекоса платформы. Для облегчения определения положения грузов и более точной их установки на платформе нанесены радиальные линии и концентрические окружности на определенном расстоянии друг от друга (5 мм).
Вращательный импульс, необходимый для запуска крутильных колебаний, сообщается платформе путем поворота верхнего диска вокруг оси. Это достигается с помощью рычага, закрепленного на верхнем диске. При таком возбуждении почти полностью отсутствуют другие виды колебаний, наличие которых затрудняет измерения. При измерениях недопустимо пользоваться амплитудами колебаний, большими 10°.
Измерение времени колебаний может проводиться или с помощью ручного секундомера или с помощью таймера.
Проведение экспериментаЗадание 1. Измерение момента инерции пустой платформы
Измерения и обработка результатов
1. Момент инерции пустой платформы Jпл определяется по формуле (3.16). При этом период колебаний пустой платформы Т и его погрешность определяются на опыте, а величины l, R, r, m и их погрешности даются, как постоянные установки.
2. Сообщают платформе вращательный импульс и измеряют время t некоторого числа (N = 15 –20) полных колебаний. Такие измерения повторяют 3 – 5 раз. Полученные результаты заносят в таблицу 3.1 отчета.
3. По экспериментальным данным для каждого опыта находят значение периода крутильных колебаний.
4. Находят среднее значение ![]() и полную погрешность
периода колебаний. При этом систематическая погрешность в измерении периода
может быть взята равной
и полную погрешность
периода колебаний. При этом систематическая погрешность в измерении периода
может быть взята равной ![]() .
.
5. Вычисляют момент инерции платформы JплЭ . Находят величину относительной и абсолютной погрешности для момента инерции платформы.
6. Рассчитывают теоретически момент инерции платформы JплT, исходя из ее массы и размеров. Находят погрешность такого расчета.
7. Сравнивают измеренное на опыте и вычисленное теоретически значение момента инерции пустой платформы. Указывают на сколько процентов экспериментальное
значение отличается от теоретического: 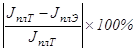 .
.
Задание 2. Определение моментов инерции тел заданной формы
Измерения и обработка результатов
1. Платформу поочередно нагружают исследуемыми телами таким образом, чтобы их центр масс совпадал с осью вращения платформы. В качестве исследуемых тел выбираются пластины, имеющие форму квадрата, прямоугольника, равностороннего треугольника, диска, а также другие тела правильной геометрической формы.
2. Измеряют время нескольких колебаний всей системы. Для каждого тела проводят измерения 3 – 5 раз. Результаты измерений заносят в таблицу 3.2 отчета.
3. Вычисляют моменты инерции нагруженных платформ JN и их погрешности. При этом необходимо учесть, что в формулу (3.16) следует подставлять сумму масс тела и платформы, а в формуле погрешности погрешность массы равна суммарной погрешности массы платформы и тела.
4. Пользуясь тем, что момент инерции – величина аддитивная, вычисляют моменты инерции тел: JЭ = JN – JплЭ. Находят величину абсолютной и относительной погрешности для моментов инерции тел.
5. Проводят сравнение экспериментально полученных значений моментов инерции с рассчитанными теоретически (см. Приложение 3). Результаты расчетов заносят в таблицу 3.3 отчета.
Задание 3. Проверка теоремы Гюйгенса - Штейнера
Измерения
1. Для проверки теоремы Гюйгенса – Штейнера используют два или несколько одинаковых тел, имеющих цилиндрическую форму.
2. Устанавливают грузы в центре платформы, положив их один на другой. Возбуждают крутильные колебания платформы. Измеряют время t нескольких колебаний (N= 15 – 20). Данные заносят в таблицу 3.4 отчета.
3. Располагают грузы симметрично на платформе относительно оси вращения. Проводят измерение времени колебаний для 5 – 7 положений грузов, постепенно перемещая их к краям платформы. Заносят в таблицу 3.4 значения расстояний от центра масс каждого тела а до центра платформы, число колебаний N и время этих колебаний tN.
Обработка результатов
1.
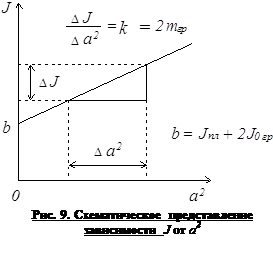 Для каждого положения грузов
определяют период колебаний грузов Ti.
Для каждого положения грузов
определяют период колебаний грузов Ti.
2. Заносят в таблицу значения а2.
3. Для каждого положения грузов находят значения момента инерции платформы с грузами Ji по формуле (3.16).
4. Полученные значения момента инерции Ji наносят на график зависимости момента инерции системы тел от квадрата расстояния центра масс грузов до оси вращения а2 (схематично эта зависимость представлена на рис. 9). Как следует из теоремы Гюйгенса – Штейнера, этот график должен быть прямой линией, с угловым коэффи-
циентом численно равным 2mгр, где mгр – масса одного груза. Кроме того, отрезок, отсекаемый от оси ординат, равен сумме моментов инерции ненагруженной платформы и моментов инерции грузов b = Jпл+ 2J0гр.
5. Из зависимости J=f(a2) определяют значение mгр и величину b. Сравнивают полученное значение с массами грузов, используемыми в работе, а также полученное значение b с расчетным значением. Совпадение этих величин (с учетом погрешностей вычислений) также подтверждает теорему Гюйгенса-Штейнера.
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ МАХОВОГО КОЛЕСА И СИЛЫ ТРЕНИЯ В ОПОРЕ
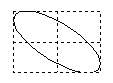
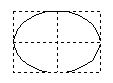
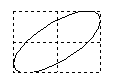
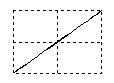
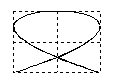
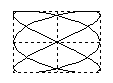
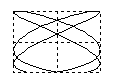
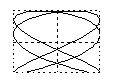
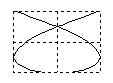
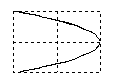
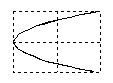
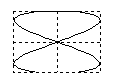
Отношение частот w2/w1 равно отношению числа касаний фигуры Лиссажу с горизонтальной и вертикальной сторонами прямоугольника, в который он вписывается.Если w1=w2, то фигуры Лиссажу имеют форму эллипса: Такие колебания называются эллиптически поляризованными. На рис. 22 в верхней строке показаны частные случаи эллиптически поляризованных колебаний. Если, кроме того A1 = A2 , то траектория точки имеет вид окружности. Такие колебания называются циркулярно поляризованными (поляризованными по кругу). Если (j2 -j1) = kp (k=0; ±1;±2; ...), то эллипс вырождается в отрезок прямой и колебания называются линейно поляризованными. Сложение колебаний одного направленияПри сложении колебаний одного направления с одинаковой амплитудой А и близкими частотами w и w+Dw (Dw<<w) возникают сложные колебания, называемые биениями. Запишем уравнения колебаний:
Сложив эти выражения, получим
|
| Вид функции | Абсолютная погрешность | Относительная погрешность |
|
q=x±×××±z |
|
|
|
q=x´×××´z |
|
|
|
|
|
|
|
q=Cx C=const |
|
|
|
q=xn |
|
|
|
|
|
|
|
q=sinx |
|
dq=ctgx×Dx |
|
q=cosx |
|
dq=tgx×Dx |
|
q=tgx |
|
|
|
q=lgx |
|
|
Приложение 2. Моменты инерции тел, имеющих простую геометрическую форму
| Форма тела |
Моменты инерции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Приложение 3 . Упругие характеристики некоторых металлов и сплавов
| Материал |
Модуль Юнга Е´1010, Н/м2 |
Модуль сдвига G´1010, Н/м2 |
| Алюминий |
7,05 |
2,63 |
| Железо |
19-20 |
7,7-8,1 |
| Константан |
16,3 |
6,11 |
| Латунь |
9,7-10,2 |
3,5 |
| Медь |
10,5-13,0 |
3,5-4,9 |
| Сталь |
20-21 |
7,9-8,9 |
| Методика изучения динамики твердого тела в курсе физики профильной ... | |
|
Содержание Введение Методика изучения вращательное движение твердого тела в классах с углубленным изучением физики Конспект урока по теме ... Здесь - момент инерции маятника, при условии, что центр масс каждого груза m0 находится на оси вращения. Платформа в виде диска радиусом R=1,5 м и массой m1=180 кг вращается по инерции около вертикальной оси с частотой n=10 мин-1. В центре платформы стоит человек массой m2=60 кг. |
Раздел: Рефераты по физике Тип: курсовая работа |
| Оборудование летательных аппаратов | |
|
Практическая работа N12-6 СИСТЕМА ВОЗДУШНЫХ СИГНАЛОВ СВС-72-3 (Продолжительность практической работы - 4 часа) I. ЦЕЛЬ РАБОТЫ Целью работы ячвляется ... Действие указанных моментов относительно оси наружной рамы приводит к уходу гироскопа вокруг оси внутренней рамы и погрешности в измерении курса не вызывает. момент силы инерции M = m 77 0l 77 0a 5к 0, в результате чего маятник станет пово- |
Раздел: Рефераты по авиации и космонавтике Тип: реферат |
| Разработка алгоритмов контроля и диагностики системы управления ... | |
|
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ "ХАРКІВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ" Факультет І Кафедра "Системи та процеси ... При этом погрешности проекций кажущегося ускорения на инерциальные оси определяются как погрешностью измерений акселерометров, так и погрешностью вычисления матрицы ориентации [1 ... расположение относительно корпуса космического аппарата начального триэдра Ox"y"z". Таким образом, триэдр Ox"y"z", положение которого относительно корпуса непрерывно вычисляется ... |
Раздел: Рефераты по авиации и космонавтике Тип: реферат |
| Электричество и магнетизм | |
|
ОБЩИЙ ФИЗИЧЕСКИЙ ПРАКТИКУМ ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ Ставрополь 2005 ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ СТАВРОПОЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ... где Ѭ U и ѬI - абсолютные погрешности, вычисленные по формуле (10), а U и I - измеренные значения напряжения и тока. Из формулы (11) найдите абсолютную ошибку Ѭ R = ѭ=Rx 2. Меняя сопротивление контура через каждые 100 Ом, получить затухающие колебания, измерить амплитуды колебаний, вычислить для каждого случая логарифмические коэффициенты затухания ... |
Раздел: Рефераты по физике Тип: книга |
| Сертификация систем обеспечения микроклимата | |
|
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ (МИИТ) Кафедра "Машиноведение и сертификация транспортной техники" Ю.П. Чепульский СЕРТИФИКАЦИЯ ... Температура внутри зачерненного шара измеряется термометром, резервуар которого помещен в центр зачерненного полого шара. Измерять температуру с нормированной погрешностью после измерения скорости воздушного потока можно через 10 мин; |
Раздел: Рефераты по безопасности жизнедеятельности Тип: учебное пособие |

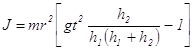 .
(4.7)
.
(4.7)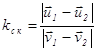 ,
(5.1)
,
(5.1)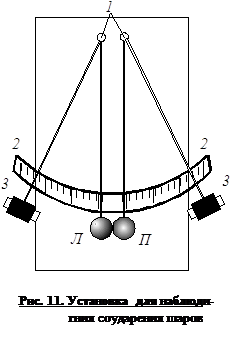 Мгновенные скорости шаров до и
после удара можно определить из закона сохранения энергии
Мгновенные скорости шаров до и
после удара можно определить из закона сохранения энергии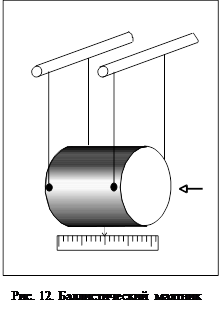 Баллистический маятник представляет
собой тяжелое тело, подвешенное на четырех нитях (рис. 12). Горизонтально
летящая пуля попадает в маятник и застревает в нем, – происходит неупругий
удар. После удара маятник начинает качаться на нитях, так что его продольная
ось остается параллельной самой себе, центр масс перемещается по окружности, а
тело в целом движется поступательно.
Баллистический маятник представляет
собой тяжелое тело, подвешенное на четырех нитях (рис. 12). Горизонтально
летящая пуля попадает в маятник и застревает в нем, – происходит неупругий
удар. После удара маятник начинает качаться на нитях, так что его продольная
ось остается параллельной самой себе, центр масс перемещается по окружности, а
тело в целом движется поступательно. Учитывая, что h<<R, получаем: 2Rh = s2. Определяя отсюда h и подставляя в (6.3), получаем
рабочую формулу метода
Учитывая, что h<<R, получаем: 2Rh = s2. Определяя отсюда h и подставляя в (6.3), получаем
рабочую формулу метода
 Физическим маятником
называется твердое тело, совершающее под действием силы тяжести колебания
вокруг неподвижной горизонтальной оси О, не проходящей через центр масс С
тела (рис. 15).
Физическим маятником
называется твердое тело, совершающее под действием силы тяжести колебания
вокруг неподвижной горизонтальной оси О, не проходящей через центр масс С
тела (рис. 15).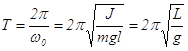 ,
(7.7)
,
(7.7)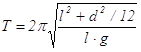 ,
(7.8)
,
(7.8) 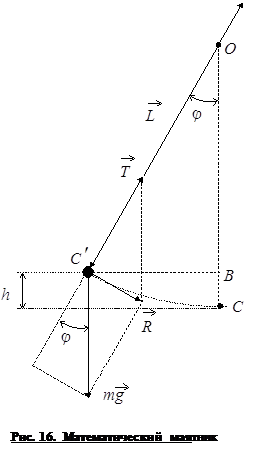 Теория
Теория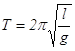 .
(8.9)
.
(8.9)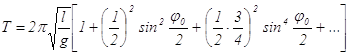 .
(8.10)
.
(8.10)
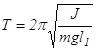 ,
(9.1)
,
(9.1)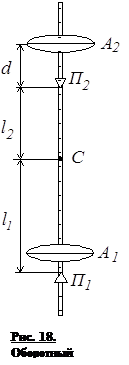 где J0 -
момент инерции относительно оси, проходящей через центр тяжести и параллельной
оси качаний, а величины J, m и l1 те же, что и в формуле (9.1).
где J0 -
момент инерции относительно оси, проходящей через центр тяжести и параллельной
оси качаний, а величины J, m и l1 те же, что и в формуле (9.1). 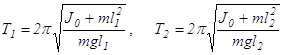 (9.3)
(9.3)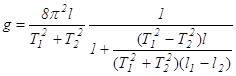 , (9.5)
, (9.5)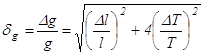 ,
(9.5)
,
(9.5) Блок-схема осциллографа
представлена на рис.19. Основной блок осциллографа – электронно-лучевая трубка (ЭЛТ),
в которой возникает и фокусируется электронный луч. Там же расположены
системы, с помощью которых можно управлять движением луча, отклоняя его в
вертикальном и горизонтальном направлениях. Движущийся луч
Блок-схема осциллографа
представлена на рис.19. Основной блок осциллографа – электронно-лучевая трубка (ЭЛТ),
в которой возникает и фокусируется электронный луч. Там же расположены
системы, с помощью которых можно управлять движением луча, отклоняя его в
вертикальном и горизонтальном направлениях. Движущийся луч 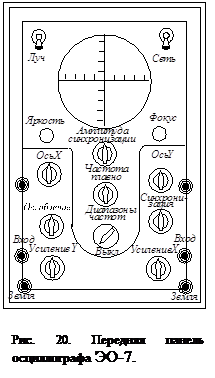 Сигнал, подаваемый на Y-вход, подводится к левым клеммам «Вход»
и «Земля». Амплитуда сигнала регулируется усилителем У1,
управляемым ручками «Усиление Y» (плавная регулировка) и «Ослабление» (грубая
регулировка», расположенными в левой части панели.
Сигнал, подаваемый на Y-вход, подводится к левым клеммам «Вход»
и «Земля». Амплитуда сигнала регулируется усилителем У1,
управляемым ручками «Усиление Y» (плавная регулировка) и «Ослабление» (грубая
регулировка», расположенными в левой части панели. Генератор ГЗ-33
предназначен для получения синусоидальных электрических колебаний звуковой частоты
от 20 до 200000 Гц. Амплитуда колебаний регулируется усилителем
мощности. На выходе колебания подаются на вольтметр и делитель напряжения (аттенюатор),
которой позволяет изменять выходное напряжение в широких пределах.
Генератор ГЗ-33
предназначен для получения синусоидальных электрических колебаний звуковой частоты
от 20 до 200000 Гц. Амплитуда колебаний регулируется усилителем
мощности. На выходе колебания подаются на вольтметр и делитель напряжения (аттенюатор),
которой позволяет изменять выходное напряжение в широких пределах.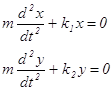 ,
(10.1)
,
(10.1)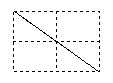
 (во втором множителе пренебрегаем
членом Dw/2,
который значительно меньше w).
(во втором множителе пренебрегаем
членом Dw/2,
который значительно меньше w).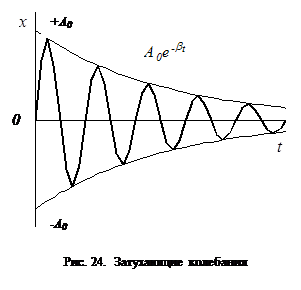 Затухающими колебаниями называются
колебания, энергия которых уменьшается с течением времени вследствие действия
на колебательную систему сил сопротивления (трения). Если принять, что сила
трения пропорциональна скорости колеблющегося тела
Затухающими колебаниями называются
колебания, энергия которых уменьшается с течением времени вследствие действия
на колебательную систему сил сопротивления (трения). Если принять, что сила
трения пропорциональна скорости колеблющегося тела 
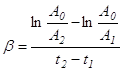 . (10.12)
. (10.12)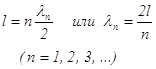 (11.1)
(11.1)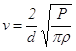 (11.3)
(11.3)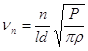 (11.4)
(11.4)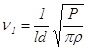 (11.5)
(11.5) В схеме установки,
представленной на рисунке 26, струна из медной проволоки натягивается на некоторой
высоте между двумя стойками-струбцинами. Один конец струны закреплен
неподвижно, а к другому концу, перкинутому через блок, прикреплена платформа с
грузами, с помощью которых в струне создается натяжение.
В схеме установки,
представленной на рисунке 26, струна из медной проволоки натягивается на некоторой
высоте между двумя стойками-струбцинами. Один конец струны закреплен
неподвижно, а к другому концу, перкинутому через блок, прикреплена платформа с
грузами, с помощью которых в струне создается натяжение. Схема установки изображена на
рисунке 27. Громкоговоритель Г, излучающий звуковые волны, закреплен на
одном конце широкой трубы. Противоположный конец трубы либо открыт, либо закрыт
заглушкой. Для предотвращения появления отраженной волны заглушка имеет
прокладку из мягкого пористого материала (паралона). Питание громкоговорителя
осуществляется от звукового генератора ЗГ. Вся установка смонтирована на
измерительной скамье, вдоль которой может перемещаться микрофон М.
Положение микрофона определяется с помощью масштабной линейки, укрепленной на
скамье. Громкоговоритель Г испускает звуковую волну некоторой фазы j1. Эта звуковая волна достигает
микрофона с фазой j2 и
порождает в его цепи переменное напряжение. Между переменным напряжением на
выходе звукового генератора и напряжением, возникающим в цепи микрофона,
существует сдвиг фаз Dj = j2 -j1, зависящий от взаимного расположения микрофона и громкоговорителя. При
перемещении микрофона по измерительной скамье на расстояние Dl = nl, составляющее целое число волн,
разность фаз Dj изменяется на 2pn. Если измерить расстояние Dl между двумя положениями микрофона,
соответствующее разности фаз Dj=2p, то, используя формулу (12.1), можно
вычислить скорость звука в воздухе:
Схема установки изображена на
рисунке 27. Громкоговоритель Г, излучающий звуковые волны, закреплен на
одном конце широкой трубы. Противоположный конец трубы либо открыт, либо закрыт
заглушкой. Для предотвращения появления отраженной волны заглушка имеет
прокладку из мягкого пористого материала (паралона). Питание громкоговорителя
осуществляется от звукового генератора ЗГ. Вся установка смонтирована на
измерительной скамье, вдоль которой может перемещаться микрофон М.
Положение микрофона определяется с помощью масштабной линейки, укрепленной на
скамье. Громкоговоритель Г испускает звуковую волну некоторой фазы j1. Эта звуковая волна достигает
микрофона с фазой j2 и
порождает в его цепи переменное напряжение. Между переменным напряжением на
выходе звукового генератора и напряжением, возникающим в цепи микрофона,
существует сдвиг фаз Dj = j2 -j1, зависящий от взаимного расположения микрофона и громкоговорителя. При
перемещении микрофона по измерительной скамье на расстояние Dl = nl, составляющее целое число волн,
разность фаз Dj изменяется на 2pn. Если измерить расстояние Dl между двумя положениями микрофона,
соответствующее разности фаз Dj=2p, то, используя формулу (12.1), можно
вычислить скорость звука в воздухе: Если момент пары сил,
приложенных касательно к незакрепленному концу проволоки, равен М, то
угол кручения (угловое смещение колебательной системы) по закону Гука оказывается
равным j = сМ,
где с –
коэффициент, зависящий от упругих свойств материала проволоки. Модуль
кручения f, равный
Если момент пары сил,
приложенных касательно к незакрепленному концу проволоки, равен М, то
угол кручения (угловое смещение колебательной системы) по закону Гука оказывается
равным j = сМ,
где с –
коэффициент, зависящий от упругих свойств материала проволоки. Модуль
кручения f, равный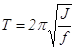 .
(13.8)
.
(13.8)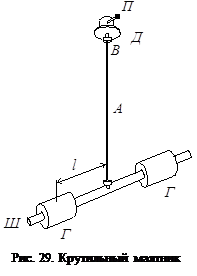 В данной работе крутильный
маятник представляет собой штангу Ш, подвешенную на проволоке А
(рис. 29). Верхний конец проволоки закреплен с помощью винта В в
держателе Д. Для выведения маятника из положения равновесия, т. е. для
первоначального закручивания проволоки служит пусковое устройство П.
Вдоль штанги могут перемещаться два груза Г одинаковой массы m. Изменяя расстояния l от грузов до центра штанги, можно
изменять момент инерции маятника, а вместе с этим и период колебаний маятника.
В данной работе крутильный
маятник представляет собой штангу Ш, подвешенную на проволоке А
(рис. 29). Верхний конец проволоки закреплен с помощью винта В в
держателе Д. Для выведения маятника из положения равновесия, т. е. для
первоначального закручивания проволоки служит пусковое устройство П.
Вдоль штанги могут перемещаться два груза Г одинаковой массы m. Изменяя расстояния l от грузов до центра штанги, можно
изменять момент инерции маятника, а вместе с этим и период колебаний маятника.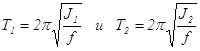 ,
(13.9)
,
(13.9)
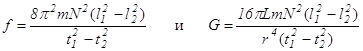 . (13.16)
. (13.16)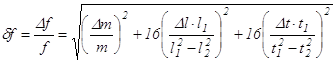 ,
,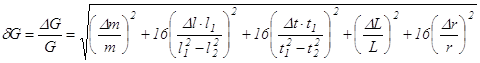 . (13.17)
. (13.17) где s = F/S
– нормальное напряжение (отношение силы F, приложенной перпендику-
где s = F/S
– нормальное напряжение (отношение силы F, приложенной перпендику-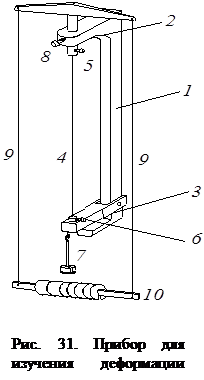 грузы. Для удобства закрепления
проволоки верхний зажим сделан подвижным и может фиксироваться с помощью винта 8. Для того чтобы верхний
кронштейн во время измерений находился под постоянной нагрузкой и имел
постоянный изгиб, к нему на тягах 9 подвешена горизонтальная планка 10.
На неё перед измерениями навешиваются все грузы, которые затем перекладываются
на платформу. Прибор устанавливается (обычно крепится к стене) в вертикальном
положении.
грузы. Для удобства закрепления
проволоки верхний зажим сделан подвижным и может фиксироваться с помощью винта 8. Для того чтобы верхний
кронштейн во время измерений находился под постоянной нагрузкой и имел
постоянный изгиб, к нему на тягах 9 подвешена горизонтальная планка 10.
На неё перед измерениями навешиваются все грузы, которые затем перекладываются
на платформу. Прибор устанавливается (обычно крепится к стене) в вертикальном
положении.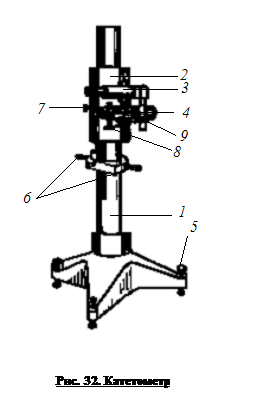 Зрительная труба 3 укреплена на каретке.
Фокусировка трубы на выбранную точку объекта производится вращением маховичка 9.
Сбоку на тубусе имеется цилиндрический уровень, ось которого параллельна
визирной оси трубы. Уровень устанавливается в горизонтальном положении
микрометрическим винтом путем совмещения изображения концов пузырька, рассматриваемого
через окуляр зрительной трубы. При совмещении половинок пузырька визирная ось
зрительной трубы принимает строго горизонтальное положение.
Зрительная труба 3 укреплена на каретке.
Фокусировка трубы на выбранную точку объекта производится вращением маховичка 9.
Сбоку на тубусе имеется цилиндрический уровень, ось которого параллельна
визирной оси трубы. Уровень устанавливается в горизонтальном положении
микрометрическим винтом путем совмещения изображения концов пузырька, рассматриваемого
через окуляр зрительной трубы. При совмещении половинок пузырька визирная ось
зрительной трубы принимает строго горизонтальное положение.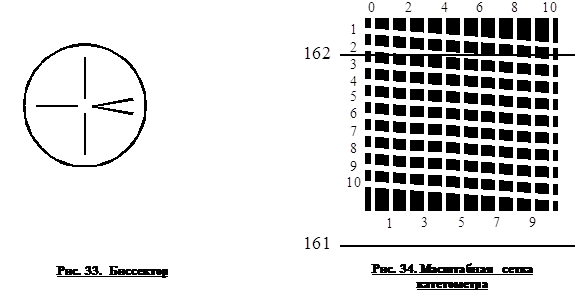 После этого снимают первый отсчет
по масштабной сетке. В поле зрения микроскопа одновременно видны изображения
двух штрихов миллиметровой шкалы, обозначенные крупными цифрами, и масштабная
сетка (рис. 34). Производство отсчета легко уяснить из следующего примера. На
рис.34 большой штрих располагается на масштабной сетке. Целое число миллиметров
дает большая цифра, соответствующая этому штриху; десятые доли миллиметра дает
ближайшая цифра слева над штрихом. Отсчет сотых и тысячных долей миллиметра
производится в горизонтальном направлении сетки там, где
После этого снимают первый отсчет
по масштабной сетке. В поле зрения микроскопа одновременно видны изображения
двух штрихов миллиметровой шкалы, обозначенные крупными цифрами, и масштабная
сетка (рис. 34). Производство отсчета легко уяснить из следующего примера. На
рис.34 большой штрих располагается на масштабной сетке. Целое число миллиметров
дает большая цифра, соответствующая этому штриху; десятые доли миллиметра дает
ближайшая цифра слева над штрихом. Отсчет сотых и тысячных долей миллиметра
производится в горизонтальном направлении сетки там, где