Лабораторная работа: Структурні дефекти кристалічної решітки

Практична робота №4

Структурні дефекти кристалічної решітки

До структурних дефектів відносяться геометричні відхилення елементів решітки від регулярного розташування в ідеальних решітках.

Класифікація можливих структурних дефектів у ґратах кристала можлива на основі просторової довжини. Ми розрізняємо, тому крапкові, лінійні й поверхневі дефекти або відповідно нуль - мірні, одномірні й двомірні дефекти. Найважливіші типи дефектів будови кристала наведені нижче.

Крапкові дефекти: дефекти по Френкелю, дефекти по Шоттки, антидефекти поФренкелю, антидефекти по Шоттки.

Лінійні дефекти: дислокація.

Поверхневі дефекти: малокутова границя зерна, більшекутова границя зерна,дефект упакування, двійник.

Поряд із цим є безліч складних і ще маловивчених дефектів структури, наприклад скупчення крапкових дефектів в «хмари», які перевищують атомарні розміри. Різні дефекти структури часто проявляються в кристалі не в чистому виді: вони взаємно впливають один на одного й можуть реагувати один з одним.

Тому що крапкові дефекти мають у трьох кристалографічних напрямках атомарні розміри, їх називають ще атомними дефектами. Дефекти по Френкелю й по Шоттки принципово відрізняються від лінійних і поверхневих дефектів тим, що вони перебувають у тепловій рівновазі. Тому неможливо одержати ідеальні кристали при нормальній температурі. Навіть якби вони були вільні від дислокацій і не мали б яких-небудь поверхневих дефектів, при температурі, що відрізняється від 0°ДО, варто було б зважати на певну рівноважну концентрацію атомних дефектів.

Такий вид невпорядкованості називається, тому власною або термічної (термодинамічної) невпорядкованістю.

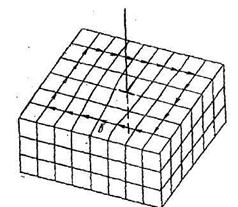
Рис. 10.8. Чотири основних типи термічних дефектів у бінарних іонних кристалах типу АВ:

а - дефект по Френкелю; б - дефект по Шоттки; в - антидефект по Френкелю;

г - антидефект по Шоттки; 1 - катіон, 2 - аннон: 3 - вакансія

Чотири основних типи термічних дефектів для бінарного іонного кристала типу АВ наведені на мал. 10.8.

Розрахунок дефектів по Шоттки можна виконати за допомогою відомих термодинамічних функцій стану. При виникненні дефектів у ґратах підвищується яквнутрішня енергіяU, так й ентропіясистеми S. Рівноважна концентрація дефектів виходить тоді з умови мінімуму вільної енергії, з рівняння F = U-T S (7.15). Отже, розрахунок концентрації дефектів зводиться до визначення величин U й S. Припустивши, що ніякої зміни обсягу не відбувається й концентрація дефектів настільки мала, що виключається взаємний вплив атомних дефектів структури, можна обчислити концентрацію дефектів по Шоттки для моноатомного кристала, тобто для кристала, що складає з атомів одного сорту.

Тому що число дефектів Шотткиn у порівнянні із загальним числом наявних у кристалі атомів мало (N>>n), те можна прийняти, що N-n N. Так що для числа вакансій, що перебувають у рівновазі при температурі Т можна записати так:

n=Ne або =e

Для концентрації дефектів по Френкелю виходить аналогічне співвідношення. Якщо N -число можливих місць для міжузлових атомів, an- число атомів, які покинули свої місця в ґратах, то

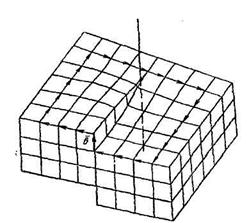
Рис. 10.9. Циркуляція (контур) Бюргерса для крайової дислокації.

Лінія дислокації перпендикулярна

 n =

 де Е - енергія утворення дефекту по Френкелю.

 У ґратах іонних кристалів типу АВз дефектами по Шоттки за принципом електричної нейтральності може виникати тільки рівне число катіонних й аніонних вакансій. У цьому випадку необхідна енергія для утворення пари вакансій. Такі види дефектів у певних кристалічних ґратах є переважними, залежить в основному від величини необхідних енергій активації.

До цієї групи дефектів структури ставляться крайові дислокації й гвинтові дислокації. Їх варто розглядати не як два принципово відрізняються типу дислокацій, а тільки як два граничних випадки, що залежать від орієнтації лінії дислокації стосовно вектора Бюргерса. Під дислокацією або лінією дислокації розуміють лінію, що відокремлює область кристала, що перетерпіла зрушення,від незрушеної. Вектор Бюргерса  дає величину й напрямок зрушення

Рис. 10.10. Циркуляція(контур) Бюргерса для гвинтової дислокації.

лінія дислокації паралельна  

атомів у кристалічних ґратах. Величина  для так званих повних дислокацій є вектор у ґратах Бравэ розглянутої структури (див. 1.2. 1). Якщо  не є вектором у ґратах Бравэ, тоді мають місце неповні або часткові дислокації. Величина вектора b , = b, є мірою дислокації.

Точно описати дислокацію можна за допомогою так називаного контуру Бюргерса, обходячи лінію дислокації в площині, що розташована перпендикулярно до цієї лінії. Таким шляхом можна або повернутися у вихідну точку, або відхилитися від її на величину, що відповідає вектору Бюргерса. На мал. 10.9 і мал. 10.10 зображена циркуляція (контур) Бюргерса для крайової й гвинтової дислокації. Крайова дислокація позначається символом . Вертикальна риса символізує всунуту атомну площина (з однієї сторони площини дислокації ґрати складаються з n+1 атомних зарядів, яким протистоять й атомних рядів). Горизонтальна риса умовно показує площину зрушення. У випадку крайової дислокації обхід по контурі Бюргерса приводить до повернення у вихідну точку, що лежить у тій же площині. Вектор Бюргерса проходить у цьому випадку перпендикулярно до напрямку дислокації (визначення крайової дислокації).

У випадку гвинтової дислокації (мал. 10.10) один оберт дає відхилення від вихідної точки на величину трансляції, що відповідає вектору Бюргерса й напрямок якої проходить паралельно лінії дислокації (визначення гвинтової дислокації). У загальному випадку лінія дислокації скривлена й розрізняють одночасно крайову й гвинтову компоненти дислокації.

З мал. 10.9 треба, що крайова дислокація являє собою лінійне розташування атомів, координація яких відрізняється від нормальної координації. У найближчому оточенні гвинтової дислокації координаційний багатогранник хоча й зберігається, але він також сильно перекручений. Дислокація представляє, таким чином, місце скупчення додаткової енергії в кристалі, тому що один ряд атомів стосовно своїх сусідів перебуває в перекрученому положенні.

Дислокації можуть виникнути, наприклад, при механічному навантаженні кристала. На мал. 10.11 показане утворення крайової дислокації при механічному зрушенні верхньої частини ґрати (мал. 10.11, а). При впливі здвигової напруги дислокація переміщається через кристал (мал. 10.11, б) і, зрештою, виходить на його поверхню мал. 10.11, в). При цьому на поверхні виникає елементарна сходинка, висота якої відповідає величині вектора Бюргерса. Залежно від числа дислокацій, що пересунулися, в одній площині ковзання виникаючий щабель ковзання може бути кратний елементарного щабля.

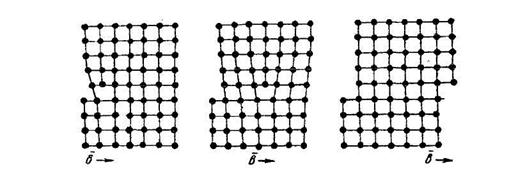
         Рис. 10.11. Виникнення й пересування крайової дислокації

         Дислокації не можуть починатися або закінчуватися у середині одного кристала кінцевих розмірів. Вони замикаються усередині з утворенням дислокаційного кільця або виходять на поверхню з утворенням дислокаційної петлі.

У кожній певній структурі стійкі тільки деякі вектори Бюргерса ( а значить і дислокації). Причина полягає в так званих дислокаційних реакціях при,яких дислокації з нестійкими векторами Бюргерса розщеплюються з виділенням енергії й утворенням стабільних дислокацій. Тому дислокаційна реакція, подібно хімічної реакції, має певний тепловий ефект Q. Якщо енергія Q вивільняється при розщепленні однієї дислокації з більшим вектором Бюргерса на дві з меншими векторами, то реакція буде протікати мимовільно.

Цей процес розщеплення буде відбуватися доти, поки не залишиться лише невелика кількість векторів Бюргерса (векторів ковзання),які звичайно відповідають найкоротшим відстаням у ґратах Бравє (при повних дислокаціях).

Дислокації не можуть виникати в бездефектному кристалі при однорідному нагріванні так як за рахунок чисто теплового руху часток. Енергія активації, необхідна для виникнення дислокацій, не може бути забезпечена коливаннями ґрат (вони можуть викликати перекручування тільки в областях атомних розмірів). Тому дислокації можуть виникнути тільки при дії зовнішньої напруги. Якщо кристал уже має дислокації, наприклад, дислокації, що виникли при його росту, то достатні вже досить малі напруги, щоб підвищити концентрацію дислокацій за рахунок так званих процесів розмноження.

Для характеристики реальної структури, що містить дислокації, використають поняття щільності дислокацій, розуміючи під цим число дислокацій, які проходять через одиницю поверхні в 1 див . Щільність дислокацій у кристалів може коливатися від 0 до 10¹² див². Вона залежить від умов одержання кристалів і наступної їхньої обробки. Щільність дислокацій сильно підвищується завдяки механічним впливам. При виконанні належних умов вирощування кристалів зараз вдається виготовляти більші бездислокаційні кристали деяких речовин, наприклад кремнію й германія.

Рис. 10.15. Малокутова границя зерен, побудована із крайових дислокацій

Найважливіші поверхневі (двомірні) дефекти структури - границі зерен, дефекти впакування й двійники. Дислокації можуть мати особливі розташування в кристалі й створювати границі між зернами. Границями зерен відокремлюються ділянки кристала, які розрізняються по своїй орієнтації. Границя між зернами вважається малокутовим, якщо оріентаційно розходження між ділянками, що примикають, кристала мало. Кут нахилу має величину всього лише від декількох секунд до декількох хвилин, однак у граничному випадку може становити від 10 до 20 град. У найпростішому випадку границя зерна будується з одного виду дислокацій, наприклад, тільки із крайових дислокацій (мал. 10.15). Обидві області кристала по обох сторони границі зерен взаємно нахилений друг до друга, причому ребро двогранного кута розташовано уздовж границі зерен.

Для більш кутових границь зерен прості дислокаційні моделі вже не придатні, тому що кут розоріетировано занадто великий. У таких випадках приймають, що в граничному шарі кристали розупорядковані настільки, що можна говорити про розчиноподібний шар (шар Бейлбі). Якщо енергію розупорядковані в перекрученому проміжному шарі більшкутової границі зерен віднести до одного атома, то її можна зрівняти з теплотою плавлення, віднесеної до одного атома. Ніякого кристалографічношо певного перехідного шару тут не є (мал. 10.16, а). Завдяки новим експериментам була створена більше ймовірна модель більш кутової границі (мал. 10.16. б). По цій моделі ширина міжзернової границі значно менше, від одного до двох періодів ґрат. Границя зерен містить кілька атомів, які належать одночасно обом ґратам (наприклад, А), інші ж атоми не належать ні однієї з них (наприклад, В). Ця модель границі зерен має більше високий ступінь упорядкованості, чим модель Бейлбі.

Дефекти впакування, що спостерігаються переважно в металевих кристалах і деяких шаруватих структурах, є порушеннями в нормальному порядку шарів при побудові структури. При цьому число найближчих сусідів у розглянутого атома, тобто координаційне число, залишається постійним, тільки взаємне розташування сусідніх атомів у другий і більше високій координаційній сфері відхиляється від ідеального стану.

Тому енергетичні розходження структур, що містять дефекти упакування, дуже малі, а, отже, і енергія дефекту впакування також невелике. Енергія розупорядкування для таких дефектів, тому мало в порівнянні з теплотою плавлення.

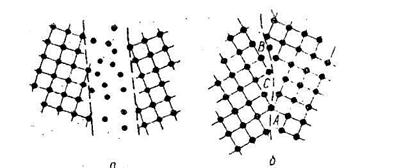
Рис. 10.16. Моделі границі зерен (по Фріделю): а - шар Бейлбі; б - реальна границя

Рис. 10.17. Когерентний двійник (правадвійниковаобластьвиникла шляхом відбиття вплощини двійникування)

Двійники також належать до двомірних дефектівструктури. Вони можуть виникати різними способами, наприклад, під час росту кристалів (двійники росту) і при механічному впливі (деформаційні        двійники, механічне двійникування).

У найпростішому випадку ми можемо уявити собі структуру двійника як результат «дзеркального» відбиття кристалічної ділянки у двійникової площини, що звичайно має простий символ. Так на мал. 10.17 двійникової площиною є площина (112). Сусідні кристалічні ділянки перебувають у положенні двійників. Кристалічна структура двійника, що виходить шляхом відбиття, така ж, як й в основної структури; розрізняється тільки їхня орієнтація.