Лабораторная работа: Тепловые эффекты химических реакций
Самостоятельная работа № 1
Вариант № 8
1.Вывести аналитическую зависимость теплового эффекта (Дж) реакции от температуры Т:
![]()
Стандартный тепловой эффект
![]() и уравнение
зависимости
и уравнение
зависимости ![]() из
приложения 1.
из
приложения 1.
2.Вычислить тепловой эффект при температуре Т=500 К.
3.Построить графики зависимости:
![]()
![]() и
и ![]() - в том интервале температур, для
которого справедливо выведенное уравнение зависимости
- в том интервале температур, для
которого справедливо выведенное уравнение зависимости ![]()
4.Определить графически ![]() как
как ![]() при
при ![]() и сравнить полученный
результат с рассчитанным по формуле
и сравнить полученный
результат с рассчитанным по формуле ![]()
Решение.
Таблица 1
| Вещество |
|
|
Температурный интервал | ||
|
|
|
|
|||
|
|
-601,49 | 48,98 | 3,14 | -11,44 | 298…3000 |
|
|
-241,8 | 30,0 | 10,71 | 0,33 | 298…2500 |
|
|
-924,6 | 46,99 | 102,85 | - | 298…541 |
|
|
- | 78,98 | 13,85 | -11,11 | 298…541 |
|
|
- | 46,99 | 102,85 | - | 298…2500 |
|
|
-16,9 | 31,99 | -89 | -11,11 | 298…2500 |
|
|
81,3 | - | - | - |
Из данных, приведенных в таблице, получаем:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Проверяем ![]()
С учетом последнего выражения
найдем ![]() интегрированием
уравнения Кирхгофа в пределах от 298 до Т (Т £ 1000):
интегрированием
уравнения Кирхгофа в пределах от 298 до Т (Т £ 1000):
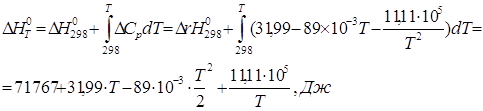
Результаты расчетов по уравнениям представлены в табл. 2.
Таблица 2
| T, К |
|
|
|
|
| 300 | 70,791 | 77,760 | -6,969 | 81060 |
| 325 | 72,963 | 80,331 | -7,368 | 80880 |
| 350 | 74,758 | 82,903 | -8,145 | 80690 |
| 375 | 76,273 | 85,474 | -9,201 | 80470 |
| 400 | 77,576 | 88,046 | -10,47 | 80220 |
| 425 | 78,715 | 90,618 | -11,903 | 79440 |
| 450 | 79,726 | 93,189 | -14,74 | 79620 |
| 475 | 80,635 | 95,761 | -15,126 | 79260 |
| 500 | 81,461 | 98,332 | -16,871 | 78860 |
| 525 | 82,222 | 100,90 | -18,678 | 78410 |
| 541 | 82,667 | 102,55 | -19,883 | 77920 |
На рис. 1 и 2 представлено
изменение ![]() ;
;
![]() и
и ![]() в зависимости от
температуры, а также определение
в зависимости от
температуры, а также определение ![]() при Т1 = 310 К.
при Т1 = 310 К.
Строим графики зависимостей:
![]()
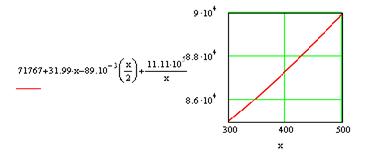
![]() и
и ![]()

Определяем графически![]() , как
, как ![]() при
при ![]() и сравниваем полученный
результат с рассчитанным по формуле
и сравниваем полученный
результат с рассчитанным по формуле
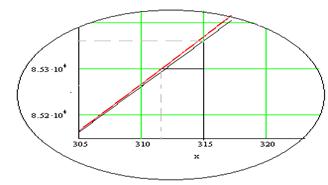
![]()
по модулю ![]()
Самостоятельная работа № 2
Вариант № 8
В таблице 1 для некоторого
чистого вещества ![]() приведены молекулярная масса
приведены молекулярная масса ![]() (кг/кмоль), плотности
в твердом и жидком состояниях (
(кг/кмоль), плотности
в твердом и жидком состояниях (![]() и
и ![]() в кг/м3) при температуре
трехфазного равновесия (тройная точка), и экспериментальные данные [2] по упругости
паров над твердым и жидким веществом при разных температурах. Необходимо:
в кг/м3) при температуре
трехфазного равновесия (тройная точка), и экспериментальные данные [2] по упругости
паров над твердым и жидким веществом при разных температурах. Необходимо:
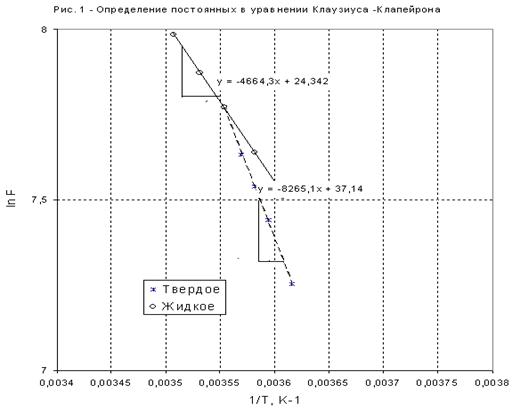
1)
по графикам зависимостей
![]() от
от ![]() или аналитически
рассчитать численные значения постоянных коэффициентов в интегральных уравнениях
Клаузиуса — Клапейрона
или аналитически
рассчитать численные значения постоянных коэффициентов в интегральных уравнениях
Клаузиуса — Клапейрона
![]()
2) вычислить средние для исследованных интервалов температур теплоты испарения, возгонки и плавления; определить координаты тройной точки (параметры трехфазного равновесия);
3) вычислить величину ![]() , характеризующую
наклон линии фазового равновесия "
, характеризующую
наклон линии фазового равновесия "![]() " в тройной точке;
" в тройной точке;
4) построить диаграмму фазовых равновесий вещества;
5) вычислить температуру плавления вещества при заданном внешнем давлении Р (Па) и оценить нормальную температуру кипения;
6) рассчитать изменение внутренней энергии, энтальпии, свободных энергий Гиббса и Гельмгольца для процесса равновесной возгонки 1 моля вещества при температуре тройного равновесия.
Таблица 1
| Вариант | Твёрдое состояние | Жидкое состояние | Условия | ||
|
|
|
|
|
||
| 8 |
276,6 278,2 279,2 280,2 281,4 |
1413 1706 1879 2066 2372 |
277,2 279,2 281,4 283,2 285,2 288,7 |
1826 2082 2372 2626 2932 3279 |
|
Решение:
1. Интегрирование уравнения
Клаузиуса — Клапейрона в предположении постоянства теплот испарения и возгонки ![]() ,
, ![]() дает выражения:
дает выражения:
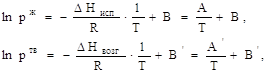
потенцирование, которых приводит к зависимости в явном виде давлений насыщенных паров от температуры:
![]()
Графики линейных зависимостей
![]() от
от ![]() представлены на
рис. 3 по данным, приведенным в табл. 5.
представлены на
рис. 3 по данным, приведенным в табл. 5.
По положению прямых на рис.
3 возможно графическое определение постоянных А и В в уравнениях ![]() . После чего теплоты испарения
и возгонки можно определить из соотношений:
. После чего теплоты испарения
и возгонки можно определить из соотношений: ![]() и
и ![]() . Такие расчеты связаны с ошибками
из-за достаточно произвольного проведения прямых линий по экспериментальным точкам.
. Такие расчеты связаны с ошибками
из-за достаточно произвольного проведения прямых линий по экспериментальным точкам.
Для более точного аналитического
расчета параметров уравнения Клаузиуса — Клапейрона воспользуемся методом наименьших
квадратов. Постоянные А и В уравнения ![]() , где
, где ![]() и
и ![]() , можно рассчитать из известных соотношений:
, можно рассчитать из известных соотношений:
Таблица 5
| Равновесие твёрдое вещество — газ | |||||||
|
|
|
|
|
|
|
|
|
| 1 | 1413 | 7,2535 | 276,6 | 0,00361 |
1,300×10–5 |
0,0261 | 1421 |
| 2 | 1706 | 7,4419 | 278,2 | 0,00359 |
1,288×10–5 |
0,0267 | 1687 |
| 3 | 1879 | 7,5385 | 279,2 | 0,00358 |
1,281×10–5 |
0,0271 | 1877 |
| 4 | 2066 | 7,6334 | 280,2 | 0,00356 |
1,267×10–5 |
0,0274 | 2086 |
| 5 | 2372 | 7,7715 | 281,4 | 0,00355 |
1,260×10–5 |
0,0279 | 2365 |
| n = 5 | 37,6388 | 0,01789 |
6,396∙10–5 |
0,1352 |
Равновесие жидкость — газ
| i |
|
|
|
|
|
|
|
| 1 | 1826 | 7,50988 | 277,2 | 0,00360 |
1,296×10–5 |
0,0270 | 1836,324 |
| 2 | 2082 | 7,64108 | 279,2 | 0,00358 |
1,281×10–5 |
0,0273 | 2071,554 |
| 3 | 2372 | 7,77148 | 281,4 | 0,00355 |
1,260×10–5 |
0,0275 | 2360,579 |
| 4 | 2626 | 7,87321 | 283,2 | 0,00353 |
1,246×10–5 |
0,0277 | 2622,843 |
| 5 | 2932 | 7,98344 | 285,2 | 0,00350 |
1,225×10–5 |
0,0279 | 2943,963 |
| 6 | 3279 | 8,09529 | 288,7 | 0,00346 |
1,197×10–5 |
0,0281 | 3589,551 |
| n = 6 | 46,874 | 0,02122 |
7,511×10–5 |
0,1655 |
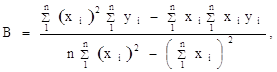
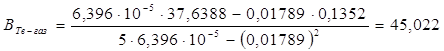
![]()
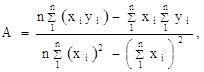
![]()
![]()
где n — число измерений. При использовании данных таблицы получим:
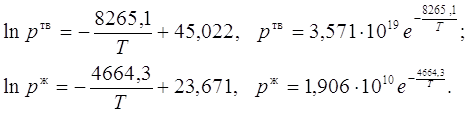
2. Из полученных уравнений рассчитываем среднюю теплоту испарения и возгонки:
![]()
![]() .
.
Теплоту плавления вещества в тройной точке найдем по закону Гесса:
DНпл = DНвозг – DНисп = 68716,04−38776,49=29939,55 Дж/моль.
3. Вычислим dT/dp в тройной точке из уравнения:

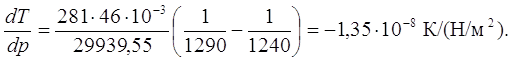
Координаты тройной точки определяем совместным решением уравнений:
Ттр.т = 281 К; Ртр.т = 2289,5 Н/м2.
4. На рис. 4 приведены кривые зависимостей давлений насыщенного пара от температуры для твердого и жидкого вещества, рассчитанные по уравнениям . Эти линии определяют параметры фазовых равновесий «тв ® газ» и «ж ® газ». При имеющейся информации линию фазовых равновесий «тв ® ж» проводим с учетом углового коэффициента этой линии в тройной точке
![]() ,
,
который считается независящим от давления (температуры). Получается практически вертикальная линия с неуловимым наклоном вправо. На диаграмме представлены исходные экспериментальные данные.
5. Температуру плавления вещества
при давлении ![]() вычислим по формуле:
вычислим по формуле:

Отсюда ![]()
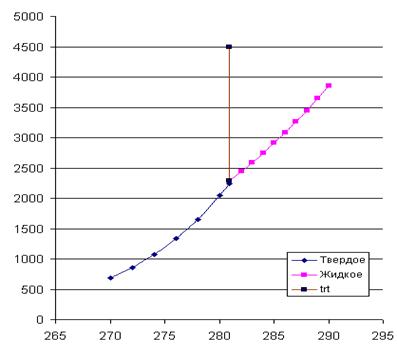
Рис. 2. Температурная зависимость давлений насыщенного пара для твердого и жидкого вещества
Нормальную температуру кипения
вещества оценим, подставив в уравнение ![]() . Получим
. Получим
![]()
6. Изменение термодинамических функций для процесса равновесной возгонки 1 моля вещества при условиях трехфазного равновесия составят:
| Энергии Гиббса |
|
| Энергии Гельмгольца |
|
| Энтальпии |
|
| Внутренней энергии |
|
Самостоятельная работа № 3
Вариант № 8
1.
Выразить ![]() и
и![]() через равновесное
число молей продукта х, если исходные вещества А и В взяты в стехиометрических количествах
при общем давлении равновесной газовой смеси Р и температуре Т, К;
через равновесное
число молей продукта х, если исходные вещества А и В взяты в стехиометрических количествах
при общем давлении равновесной газовой смеси Р и температуре Т, К;
2.
Рассчитать ![]() и
и ![]() при 300 К, если
при 300 К, если
![]()
3.
Вычислить равновесное
количество вещества С при давлении в равновесной системе ![]() и рассчитайте степень превращения
вещества А и В.
и рассчитайте степень превращения
вещества А и В.
A + B = 3C
Решение:
| А | В | 3С |
|
|
|
|
1)![]() , что говорит о том, что
смесь неравновесная
, что говорит о том, что
смесь неравновесная
![]()
Равновесные парциальные давления определим по закону Дальтона:
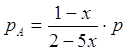 ;
;
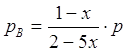 ;
;
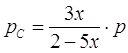
где ![]() - общее давление. Закон действующих
масс для данной реакции запишется так:
- общее давление. Закон действующих
масс для данной реакции запишется так:
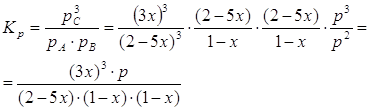
Константу ![]() находим из соотношения:
находим из соотношения:
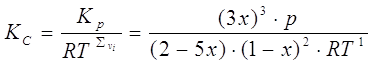
2) Расчет ![]() и
и ![]() при заданной температуре,
давлении и известном значении х
при заданной температуре,
давлении и известном значении х
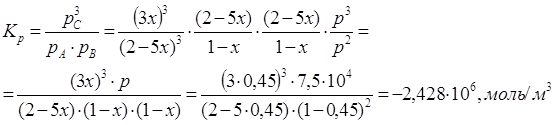
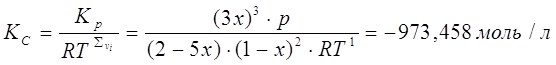
3) При изменении давления
изменяется параметр х, температура остаётся неизменной, значение ![]() не меняется.
не меняется.
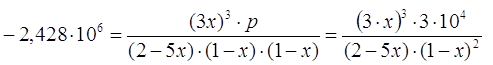
![]() молей
молей
Равновесное количество вещества равно:
![]() молей
молей
Рассчитаем степень превращения веществ А и В:
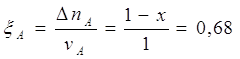
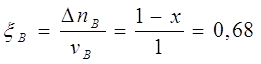
![]() , условие выполнено.
, условие выполнено.
Самостоятельная работа №4
Вариант № 8
Гетерогенная реакция между веществами А и В (табл. 1) протекает при постоянной температуре Т;
1)
определите стандартное
сродство![]() веществ
А и В при 298 К;
веществ
А и В при 298 К;
2)
вычислите константы
равновесия ![]() и
и
![]() при температуре
Т;
при температуре
Т;
3) определите количество прореагировавшего твёрдого вещества А, если объём системы V м3, а исходное давление газа В равно Р1, объёмом твердой фазы можно пренебречь;
4) определите изменение энергии Гиббса, для начала реакции, если исходное давление газообразных веществ В и С соответственно равны Р2 и Р3, реакция протекает при температуре Т, К идеально обратимо.
Таблица 1
| Реакция | Т, К |
|
|
|
|
|
|
773 | 10 | 705 | 800 | 2 |
Решение:
![]()
|
|
|
|
|
|
|
|
1) Вычисление стандартного
сродства ![]() веществ
А и В при 298 К;
веществ
А и В при 298 К;
![]()
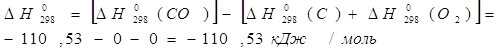
![]()
![]()
2)Вычисление констант равновесия
![]() и
и ![]() при температуре
773 К.
при температуре
773 К.
![]()
![]()


| Вещество |
|
|
Температурный интервал | ||
|
|
|
|
|||
|
|
0 | 16,86 | 4,77 | – 8,54 | 298…2500 |
|
|
0 | 31,46 | 3,39 | – 3,77 | 298…3000 |
|
|
-110,53 | 28,41 | 4,10 | – 0,46 | 298…2500 |
|
|
- | 28,41 | 4,10 | – 0,46 | 298…2500 |
|
|
- | 48,32 | 8,16 | 12,31 | 298…2500 |
|
|
-9,47 | – 19,91 | –4,06 | –12,77 | 298…2500 |
![]()
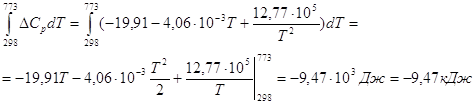
![]()

![]()
![]()
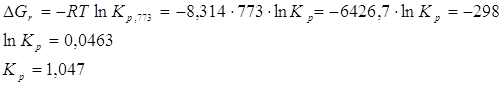
Константу равновесия ![]() можно найти из
соотношения:
можно найти из
соотношения:
![]()
3)Определение количества прореагировавшего
твёрдого углерода, если объём системы ![]() м3, а исходное давление
газа
м3, а исходное давление
газа ![]() равно
равно
![]() Па
Па
![]() , что говорит о том, что смесь неравновесная
, что говорит о том, что смесь неравновесная
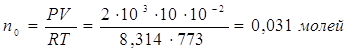
|
|
|
|
|
|
|
2 |
![]() ,
,
![]()
Равновесные парциальные давления определим по закону Дальтона:
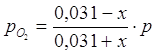 ;
;
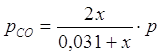 ;
;
где ![]() - общее давление. Закон действующих
масс для данной реакции запишется так:
- общее давление. Закон действующих
масс для данной реакции запишется так:

![]()
С учетом того, что углерода расходуется в 2 раза больше, чем кислорода, то количество прореагировавшего углерода составит 0,005 молей.
4) Определение изменения энергии Гиббса для начала реакции
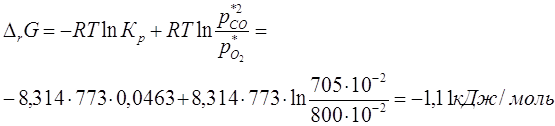
Самостоятельная работа № 5
Вариант 8
Зависимость константы равновесия
реакции от температуры (табл. 9) выражается уравнением ![]() коэффициенты a, b, c и d
приведены в табл. 1, давление выражено в Паскалях:
коэффициенты a, b, c и d
приведены в табл. 1, давление выражено в Паскалях:
1. определите константу равновесия реакции при Т, К;
2.
постройте график зависимости
![]() в интервале
температур от (Т – 100) до (Т + 100) К;
в интервале
температур от (Т – 100) до (Т + 100) К;
3. укажите, как изменяется константа равновесия при повышении температуры;
4.
определите тепловой
эффект реакции ![]() при Т, К;
при Т, К;
5. сопоставьте тепловой эффект, вычисленный в п. 4, с тепловым эффектом, вычисленным по закону Кирхгофа при температуре Т, К;
6. определите стандартное сродство реагирующих веществ при температуре Т, К.
| Реакция (А) | К | Т, К |
|
|
|
500 |
Таблица 1
| a | b | c | d |
| – 4600 | 0,623 | – 0,001 02 | 17,776 |
Решение:
1)Определение константы равновесия при 500 К.
Заменяем десятичный логарифм
натуральным, для чего умножаем обе части уравнения на ![]() .
.
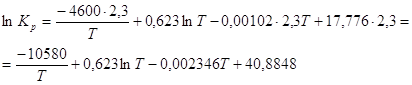
Подставляем значение Т в полученное уравнение:
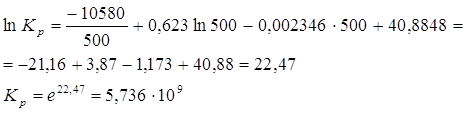
2)Построение графика зависимости
![]() в интервале
температур от 400 до 600 К;
в интервале
температур от 400 до 600 К;
|
|
|
|
|
|
|
| 400 | 7,489 | 475 | 9,724 | 550 | 10,558 |
| 425 | 8,156 | 500 | 9,747 | 575 | 10,908 |
| 450 | 8,747 | 525 | 10,173 | 600 | 11,228 |
3) Константа равновесия при повышении температуры увеличивается. Принимаем Т=1000К и повторяем расчет. Функция экспоненты в степени х является возрастающей, значит чем больше значение логарифма функции, тем больше сама функция.
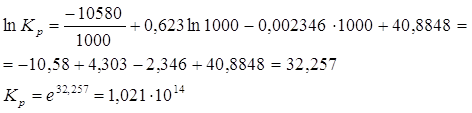
4)Определение стандартного теплового эффекта при Т=500К
![]()
![]()
![]()
5)Сопоставление теплового эффекта, вычисленного в п. 4, с тепловым эффектом, вычисленным по закону Кирхгофа при температуре 500 К;
Сначала вычисляем стандартный тепловой эффект при 298 К.
![]()
![]()
Вычисление теплоёмкостей конечных
и исходных продуктов реакции. Значения ![]() и
и ![]() взяты из приложения 1 методического
пособия.
взяты из приложения 1 методического
пособия.
![]()
![]()
![]()
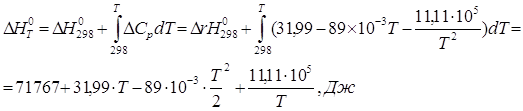
![]()
![]()
Небольшая разница возникает из-за погрешности вычисления.
6) Вычисление стандартного
сродства ![]() веществ
А и В при 500 К;
веществ
А и В при 500 К;
![]()
Самостоятельная работа №7
Вариант № 8
Вычислите константу равновесия Кр реакции при заданной температуре Т. Для расчета воспользоваться методом Темкина — Шварцмана и прил. 1 и 2.
| Реакция | Т, К |
|
|
400 |
Воспользуемся формулой:
![]()
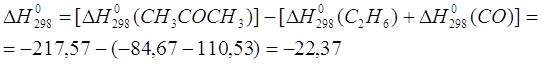
![]()
| Вещество |
|
|||
|
|
|
|
|
|
|
|
5,75 | 175,11 | — | – 57,85 |
|
|
28,41 | 4,10 | – 0,46 | — |
|
|
22,47 | 201,80 | — | – 63,50 |
|
|
22,47 | 201,80 | — | – 63,50 |
|
|
34,16 | 179,21 | – 0,46 | – 57,85 |
|
|
−11,69 | 22,59 | – 0,46 | – 5,65 |
![]()
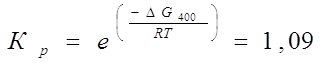
| Химия, элементы таблицы Менделеева | |
|
Седьмая группа периодической системы Из членов данной группы водород был рассмотрен ранее. Непосредственно следующие за ним элементы - F, Сl, Br и I ... Взвесить отдельную молекулу явно невозможно, однако теория открыла другой путь: надо было как-то определить число молекул в моле - так называемое число Авогадро (N ... Найденные на опыте значения равновесных концентраций (в моль/л) при различных неэквивалентных соотношениях реагирующих веществ и вычисленные из них величины константы равновесия ... |
Раздел: Рефераты по химии Тип: реферат |
| Кинетика химических и электрохимических процессов | |
|
Министерство образования и науки Российской Федерации ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Федеральное государственное образовательное учреждение ... Р е ш е н и е. Константу равновесия вычисляем по уравнению: (ѭ02 - ѭ01).n/0,0592. Рассчитаем концентрацию продукта [В] через 69 ч: [В] = = [А]0 - [Р] - [А] = = 1 - 0,061 - 0,001 = 0,938 моль/л. Вычислим время tинд, за которое устанавливается концентрация В ... |
Раздел: Рефераты по химии Тип: учебное пособие |
| Методика решения задач по теоретическим основам химической технологии | |
|
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Пензенский государственный педагогический университет им. В.Г. Белинского Факультет Кафедра Естественно ... [N2] = 0,01 моль/л, [Н2] = 2,0 моль/л, [NH3] = 0,40 моль/л. Вычислить константу равновесия и исходные концентрации азота и водорода. Вычислите константу равновесия Кр реакции CaCO3 СаО + СО2 при 800°С, если известно, что равновесное давление газа в резервуаре при этой температуре равно 3,82 атм., а при 27°С ... |
Раздел: Рефераты по химии Тип: дипломная работа |
| Химическая термодинамика | |
|
Федеральное агентство по образованию Пензенский государственный педагогический университет им. В.Г. Белинского КУРСОВАЯ РАБОТА Химическая ... Напишите уравнение, выражающее связь между тепловым эффектом при постоянном давлении и тепловым эффектом при постоянном объеме. Вычислите изменение энтропии этого перехода, если удельная теплота испарения воды при 100°С равна 2257 Дж/г, удельная теплоемкость водяного пара при давлении в 1,013*105Па равна 1 ... |
Раздел: Рефераты по химии Тип: курсовая работа |
| Разработка месторождений газоконденсатного типа | |
|
Месторождения газоконденсатного типа. В отличие от чисто газовых месторождений газоконденсатные разрабатываются для получения не только газа, но и ... Этот процесс исследуют либо расчетным путем, используя данные о константах межфазного равновесия составляющих смесь индивидуальных углеводородных компонентов, либо на сосуде ... Для исследования типичных, но сравнительно "легких" газоконденсатных смесей (молекулярная масса фракции С5+ в смеси исходного состава равна 115 г/моль) наблюдается интенсивный рост ... |
Раздел: Рефераты по геологии Тип: реферат |