Реферат: Химическая реакция в смеси идеальных газов. Константа химического равновесия в смеси идеальных газов
Состояние изотермической системы с неизменным объёмом целесообразно описывать посредством свободной энергии (функции Гельмгольца). В этих условиях она является характеристической функцией и изохорно-изотермическим потенциалом системы.
Посредством частного дифференцирования из неё далее можно извлечь прочие необходимые термодинамические характеристики, а именно:
![]() (1)
(1)
Построить явный вид функции свободной энергии для некоторых относительно простых систем можно методом статистической термодинамики.
В любом естественно протекающем (самопроизвольном или свободном) процессе свободная энергия системы понижается. При достижении системой состояния термодинамического равновесия её свободная энергия достигает минимума и уже в равновесии далее сохраняет постоянное значение. Из равновесия систему можно вывести за счёт внешних сил, повышая её свободную энергию. Такой процесс уже не может быть свободным - он будет вынужденным.
Микроскопические движения частиц и в равновесии не прекращаются, и в системе, состоящей из огромного числа частиц и подсистем любой природы, возможно множество различных частных вариантов и комбинаций отдельных частей и внутри них, но все они не выводят систему из равновесия.
Термодинамическое равновесие в макросистеме совсем не означает, что и в её микроскопических фрагментах исчезают все виды движения. Напротив, равновесие обеспечивается динамикой именно этих микроскопических движений. Они-то осуществляют непрерывное выравнивание - сглаживание наблюдаемых макроскопических признаков и свойств, не допуская их выбросов и чрезмерных флуктуаций.
Основной целью статистического метода является установление количественной связи между характеристиками механических движений отдельных частиц, составляющих равновесный статистический коллектив, и усреднёнными свойствами этого коллектива, которые доступны для термодинамических измерений макроскопическими методами.
Цель состоит в том, чтобы на основании механических характеристик движений отдельных микроэлементов равновесного коллектива вывести количественные законы для термодинамических параметров системы.
Согласно методу Гиббса термодинамическая система это коллектив - совокупность очень большого числа элементов - однотипных подсистем.
Каждая подсистема в свою очередь может также состоять из очень большого числа иных ещё более мелких подсистем и в свою очередь может играть роль вполне самостоятельной системы.
Все естественные флуктуации внутри равновесной системы равновесия не нарушают, они совместимы с устойчивым макроскопическим состоянием огромного коллектива частиц. Они просто перераспределяют признаки отдельных элементов коллектива. Возникают разные микросостояния, и все они суть версии одного и того же наблюдаемого макросостояния.
Каждая отдельная комбинация состояний элементов коллектива порождает лишь одно из огромного множества возможных микросостояний макросистемы. Все они в физическом смысле равноценны, все приводят к одному и тому же набору измеримых физических параметров системы и отличаются лишь какими-то деталями распределения состояний между элементами …
Все микросостояния совместимы с макроскопическим - термодинамическим равновесием, и числовой разброс отдельных составляющих свободной энергии (её энергии и энтропии) является вполне обычным обстоятельством. Надо понимать, что разброс возникает за счёт непрерывного обмена энергией между частицами – элементами коллектива. У одних элементов она уменьшается, но при этом у других увеличивается.
Если система находится в термостате, то ещё непрерывно осуществляется обмен энергией и с окружающей средой. Происходит естественное энергетическое перемешивание коллектива, за счёт непрерывного обмена между микрочастицами коллектива. Равновесие постоянно поддерживается через тепловой контакт с внешним термостатом. Так в статистике чаще всего именуют окружающую среду.
Создавая универсальную схему статистической механики, Гиббс использовал удивительно простой приём.
Любая реальная макроскопическая система это коллектив из огромного множества элементов – подсистем. Подсистемы могут иметь и макроскопические размеры, и могут быть микроскопическими, вплоть до атомов и молекул. Всё зависит от рассматриваемой задачи и уровня исследования.
В разные моменты времени в разных точках реальной системы, в разных пространственных регионах макроскопического коллектива мгновенные характеристики его малых элементов могут быть различны. «Неоднородности» в коллективе постоянно мигрируют.
Атомы и молекулы могут находиться в разных квантовых состояниях. Коллектив огромный, и в нём представлены различные комбинации состояний физически одинаковых частиц. На атомно-молекулярном уровне всегда происходит обмен состояниями, имеет место их непрерывное перемешивание. Благодаря этому свойства различных фрагментов макроскопической системы выравниваются, и физически наблюдаемое макроскопическое состояние термодинамической системы внешне выглядит неизменным...
Броуновское движение – главный молекулярный механизм, обеспечивающий перемешивание локальных свойств микроскопических подсистем - элементов макроскопического коллектива. Броуновское движение и ряд сопутствующих ему релаксационных процессов выравнивают в пространстве и усредняют во времени суммарные динамические характеристики макроскопического равновесного коллектива, превращая их в измеримые термодинамические параметры с равновесными значениями.
Так возникает огромное множество мгновенных различающихся суммарных состояний всего коллектива, и все они совместимы с одним и тем же внешне неизменным термодинамическим равновесием системы.
Всё множество, сколь необозримым оно бы не казалось, всевозможных комбинаций микромеханических состояний всех однотипных элементов системы, совместимых с её термодинамическими характеристиками в её определённом наблюдаемом термодинамическом (макроскопическом) состоянии, Гиббс определил как АНСАМБЛЬ.
Ансамбль напоминает ленту бесконечного фильма, кадры котрого, время от времени повторяясь, с бесконечными вариациями изображают одну и ту же сцену с некоторыми изменениями. Элементы ансамбля подобны отдельным кадрам этого бесконечного фильма.
Весь ансамбль изображает макросостояние (фильм), а его элементы суть микросостояния (кадры этого фильма).
Рассмотрим пробег химической реакции между несколькими частицами:
![]() (2)
(2)
Следуя правилам IUPAC, стехиометрические коэффициенты представим в виде массива
ni Î (-a, - b,… +k, +m, …); (3)
Стандартное сродство (стандартное приращение энергии Гиббса) определяется через стандартные химические потенциалы реагентов и продуктов и изотермой Вант-Гоффа связано с безразмерной термодинамической константой равновесия Kp:
![]() ; (4)
; (4)
Это и есть основание для расчёта константы химического равновесия.
Применяя правило ИЮПАК для стехиометрических коэффициентов, формулу (21.3) легко записать в общем виде
![]() ; (5)
; (5)
Введём стандартные химические потенциалы ![]() веществ i.
веществ i.
![]() . (6)
. (6)
Стандартное сродство реакции принимает вид
![]() ; (7)
; (7)
Сокращая на RT=NkT, получаем
![]() ; (8)
; (8)
Константа химического равновесия в смеси идеальных газов.
Совершим цепочку несложных преобразований. Вначале внесём стехиометрические коэффициенты в сумме под знак логарифма в виде показателей степеней у статистических сумм
![]() ; (9)
; (9)
Затем воспользуемся тем, что сумма логарифмов равна логарифму произведения
![]() ; (10)
; (10)
Наконец, избавляясь от логарифмов, получаем искомое статистическое выражение для константы равновесия
![]() ; (11)
; (11)
Она имеет вид произведения статистических сумм.
Константа химического равновесия в смеси идеальных газов.
![]()
![]() ; (12)
; (12)
Стандартные суммы состояний имеют вид:
- трансляционная: 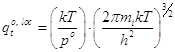 ; (13)
; (13)
- молекулярная: 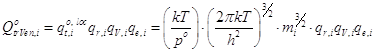 ; (14)
; (14)
Константа равновесия может рассчитываться как непосредственно в виде произведения статистических сумм,
![]() ; (15)
; (15)
которые предварительно следует рассчитать, а также по результирующей формуле
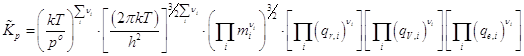 ; (21.14)
; (21.14)
При вычислении электронных сумм состояния помним, что занят один-единственный электронный уровень, и он характеризуется кратностью вырождения ge, i. Эта кратность равна числу микросостояний основного терма у атомов и у молекул. У молекул чаще всего достаточно спиновой мультиплетности, но возможно и орбитальное вырождение. Это уже зависит от конкретной частицы.
Поэтому электронная сумма состояний у молекулы определяется формулой
![]() ; (16)
; (16)
Энергия химической связи считается равной энергии её диссоциации и отсчитывается от основного колебательного уровня, а не от минимума потенциальной кривой.
Этот вопрос рассмотрен в учебнике Даниэльса и Олберти на стр.539 в разделе 17.13. Там же приводятся основные формулы. Раздел написан хорошо и достаточно просто. Этот учебник вполне пригоден для подготовки студентов.
1. Сводка статистических сумм для простейших стационарных движений.
ПРИЛОЖЕНИЕ 1. Математическая справка о факториалах больших числах.
Факториал числа, соизмеримого с числом Авогадро, непосредственно вычислить невозможно, и поэтому давно разработаны приближённые способы численно точного вычисления, основанные на применении гамма – функции Эйлера первого рода.
При очень большом числе, факториал которого вычисляется, точной становится формула Стирлинга (можете проверить прямыми вычислениями). Разность между точным и приближённым логарифмами становится относительно малой величиной:
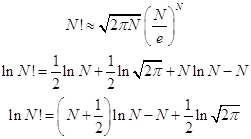
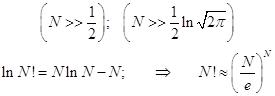
Таблица. Точные и приближённые значения логарифмов факториалов больших чисел.
| N | N! точно |
ln(N!) точно |
Стирлинг точно |
Стирлинг прибл. |
| 8 | 40320 | 10.604 | 10.594 | 8.635 |
| 9 | 362880 | 12.802 | 12.7925 | 10.775 |
| 10 | 3628800 | 15.1044 | 15.096 | 13.026 |
| 11 | 39916800 | 17.5023 | 17.4948 | 15.377 |
| 12 | 479001600 | 19.987 | 19.979 | 17.818 |
| 13 | 6227020800 | 22.55216 | 22.545 | 20.344 |
| 14 | 8.71782912*1010 | 25. 19122 | 25.185 | 22.947 |
| 20 | 2.432902008*1018 | 42.3356 | 42.33145 | 39.915 |
| 25 | 1.55112100*1025 | 58.00 | 57.998 | 55.470 |
| 50 | 3.041409*1064 | 148.478 | 148.476 | 145.601 |
ПРИЛОЖЕНИЕ 2.
Дополнительные сведения о вращательных статистических суммах.
Для справки приведём ротационные статистические суммы молекулы с учётом её внутренних вращений
Суммы по состояниям для внутреннего вращения (Ерёмин, стр.181-182):
Для свободного внутреннего вращения в этане (при высокой температуре):
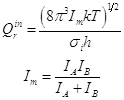
Для каждой из двух свободно вращающихся групп в сложной молекуле:
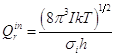
Число молекулярной вращательной симметрии требует специального анализа. Там же у Ерёмина приводятся приёмы расчёта.
Учитывая все ротационные преобразования симметрии, например, для этана получаем число 18 (3 степени свободы для вращения вокруг оси 3-го порядка вдоль связи C-C, ещё 2 - для оси 2-го порядка и также для внутреннего вращения – вновь ось 3-го порядка).
Вся ротационная сумма состояний в общем случае приобретает вид:
(Ерёмин, стр.233, формула VI.155)
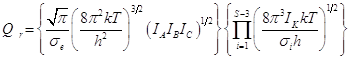 .
.
Множитель p1/2 появляется при вычислении ротационной статистической суммы методом классической статистики, тогда как вывод общей формулы на основе квантовой статистики невозможен.
Вращательные стат. суммы сложных молекул и ротационное число симметрии.
(см. Приложение – несколько страниц из книги Дж. Майер, М. Гёпперт-Майер).