Контрольная работа: Элементы статистической термодинамики
1. Распределение Гиббса и распределение Больцмана. Структурные постоянные молекул.
В случае невзаимодействующих частиц идеального газа каноническое распределение Гиббса превращается в распределение Больцмана. В качестве подсистем канонического ансамбля рассматриваются приближённо независимые молекулярные движения:
Поступательное,
Вращательное,
Колебательное,
Электронное,
Ядерное.
Статистические суммы электронного и ядерного состояний равны кратностям вырождения их основных уровней (термов). У электронного движения это число микросостояний, объединённых в терм. У ядерного движения это спиновая мультиплетность ядерного остова.
Таблица 1. Постоянные двухатомных молекул (Табл. 15.2, стр. 467, Даниэльс, Олберти).
| Молекула |
NAm - масса приведённая (эксперим), г |
R0×1010, м |
|
D, эВ | D, кДж/моль |
| Br2 | 39.958 | 2.283 | 323.2 | 1.971 | 190.2219 |
| CH | 0.930024 | 1.1198 | 2861.6 | 3.47 | 334.8909 |
| Cl2 | 17.48942 | 1.988 | 564.9 | 2.475 | 238.863 |
| CO | 6.85841 | 1.1282 | 2170.21 | 11.108 | 1072.037 |
| H2 | 0.504066 | 0.7416 | 4395.24 | 4.476 | 431.9802 |
| H2+ | 0.503928 | 1.06 | 2297 | 2.648 | 255.5594 |
| HCl | 0.979889 | 1.27460 | 2989.74 | 4.430 | 427.5406 |
| HBr | 0.99558 | 1.4138 | 2649.67 | 3.75 | 361.9136 |
| HI | 1.000187 | 1.604 | 2309.53 | 3.056 | 294.9356 |
| KCl | 18.599 | 2.79 | 280 | 4.42 | 426.5757 |
| LiH | 0.881506 | 1.5953 | 1405.649 | 2.5 | 241.2759 |
| Na2 | 11.49822 | 3.078 | 159.23 | 0.73 | 70.45255 |
| NO | 7.46881 | 1.1508 | 1904.03 | 6.487 | 626.0626 |
| O2 | 8.00000 | 1. 20739 | 1780.361 | 5.080 | 490.2726 |
| OH | 0.94838 | 0.9706 | 3735.21 | 4.35 | 419.8198 |
Таблица 2. Спиновые квантовые числа наиболее распространённых ядер:
| Элемент | Ядро изотопа |
Спин ядра I |
Мультиплетность ядерного спина 2I+1 |
| Водород | 1H | ½ | 2 |
| Водород | 2D | 1 | 3 |
| Водород | 3T | ½ | 2 |
| Азот | 14N | 1 | 3 |
| Азот | 15N | ½ | 2 |
| Фтор | 19F | ½ | 2 |
| Углерод | 12С | 0 | 1 |
| Углерод | 13С | ½ | 2 |
2. Основные формулы. Вероятности и заселённости.
Вероятности (Заселённости - мольные доли и статистические веса).
Суммы по состояниям молекулярных движений.
Мольная и молекулярная статистическая суммы.
Энтропия видов движения.
Средняя энергия коллектива.
![]()
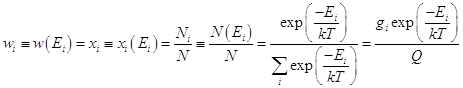
![]()
![]()
![]()
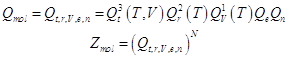
![]() - для 1 поступательной
степени свободы (приближение)
- для 1 поступательной
степени свободы (приближение)
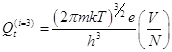 -для 3 поступательных
степеней свободы 1 частицы
-для 3 поступательных
степеней свободы 1 частицы
![]() - для 2 вращательных степеней
свободы 1 частицы
- для 2 вращательных степеней
свободы 1 частицы
(линейная молекула)
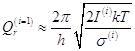 - для 1 степени свободы вращения
1 частицы (приближение)
- для 1 степени свободы вращения
1 частицы (приближение)
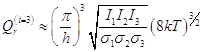 - для 3-х мерного вращения 1
частицы
- для 3-х мерного вращения 1
частицы
(общая модель)
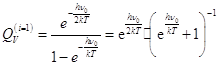 -для линейного осциллятора
-для линейного осциллятора
(1 колебательная степень свободы молекулы)
![]()
-Химический потенциал, отнесённый к одной частице (Внимание! не к молю!)
Химический потенциал и мольная концентрация.
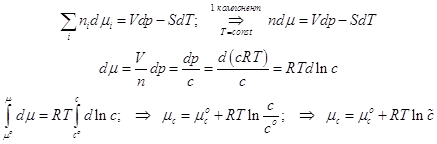
Химическое сродство и константа равновесия
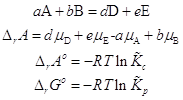
Константа химического равновесия в смеси идеальных газов
Рабочие формулы:
Вариант 1. Здесь представлены электронные суммы состояний. Их следует вычислять по отдельности. Электронные уровни должны быть выражены в единой шкале. Этот способ строгий, но менее доступный:
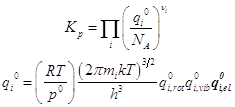
Вариант 2. Здесь представлены кратности вырождения электронных уровней и разность электронных уровней. Этот способ удобен для расчёта диссоциативных равновесий:
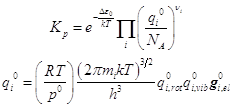
(ВНИМАНИЕ! В учебнике Даниэльса и Олберти в формулах допущены ошибки, связанные с учётом электронных состояний. Здесь ошибки исправлены)
ЗАДАЧИ (с примерами решений) (из Даниэльса – Олберти и из задачника МГУ - Ерёмин и соавторы – см. Литература)
ЗАДАЧА 1.
У молекулы с массой M четыре квантовых состояния распределены между двумя энергетическими уровнями. Спектр уровней определён в виде массива: (0, E, E, E).
Нарисуйте энергетическую диаграмму состояний.
Как называют подобные уровни?
Каковы средние мольные доли частиц, заселяющих эти уровни при температуре T?
Сколько частиц в среднем будет заселять эти уровни в коллективе из N частиц?
Какова поступательная энтропия газа с этими характеристиками в объёме V?
Каково давление этого газа?
При каких температурах:
а) - все частицы будут находиться на основном уровне?
б) - все частицы будут поровну заселять оба уровня?
В) - заселённости всех квантовых состояний равны?
Запишите выражение для средней энергии этого газа и покажите, как она изменяется с увеличением температуры?
ЗАДАЧА 2.
У молекулы с массой M три квантовых состояния относятся к трём энергетическим уровням. Спектр уровней определён в виде массива: (E1, E2, E3).
Нарисуйте энергетическую диаграмму состояний.
Рассчитайте мольные доли частиц, заселяющих эти уровни при температуре T.
Рассчитайте среднюю энергию частицы при температуре T.
Рассчитайте энергию коллектива из N частиц при температуре T.
Можете решать задачу, придав уровням определённые численные значения, например
(E1, E2, E3) = (A, B, C).
ЗАДАЧА 3.
У молекулы с массой M энергетический спектр задан массивом: (0,E1, E2).
Уровни вырождены. Их кратности вырождения равны (g1, g2, g3) =(1, 2, 3), так что коллектив из N частиц распределяется между шестью возможными квантовыми состояниями. Для этого коллектива нарисуйте энергетическую диаграмму состояний, рассчитайте мольные доли частиц, заселяющих эти уровни при температуре T, рассчитайте среднюю энергию одной частицы.
Можете придать уровням определённые значения.
ЗАДАЧА 4.
Запишите выражение поступательной статистической суммы с учётом неразличимости частиц. Рассчитайте при T=300 K поступательную энтропию:
а) газообразного аргона.
б) газообразного водорода для его трёх изотопов: протия 1H, дейтерия D (2H), трития T (3H)].
в) газообразного молекулярного азота (изотопы 14N и 15N).
ПРИМЕЧАНИЕ: Для изотопозамещённых молекул используйте приближённое (но почти точное) правило, согласно которому силовая константа колебания не изменяется при замене атома его изотопом.
ЗАДАЧА 5.
Запишите выражение поступательной вращательной статистической суммы при T=300 K с учётом числа симметрии молекул.
Рассчитайте вращательную энтропию:
а) молекулярного азота (изотоп 14N) при T=300 K.
б) молекулярного кислорода (изотоп 16O) при T=300 K.
Недостающие данные можно взять из справочника
ЗАДАЧА 6.
Запишите выражение колебательной статистической суммы при T=300 K с учётом числа симметрии молекул. Рассчитайте колебательную энтропию:
а) молекулярного водорода для его трёх изотопов (1H; 2D; 3T) при T=300 K.
б) молекулярного азота (изотоп 14N).
Недостающие данные можно взять из справочника.
ЗАДАЧА 7.
Рассчитать при 298 К константу равновесия для реакции изотопного обмена: D+H2=H+DH.
Считать, что равновесные расстояния и энергии диссоциации молекул H2 и DH одинаковы.
(Ответ в учебнике Д-О: K=7.17 ).
РЕШЕНИЕ
Таблица 1. Структурные параметры молекул и изотопов атома водорода.
|
Qяд= = gяд |
Qэл= = gэл |
M, у. е. | , у. е. | |
|
D, кДж/моль | |
| D | 3 | 2 | 2 | | - | ||
| H2 | 1(+3) | 1 | 2 | ½ | 2 | 4395.24 | 431.9802 |
| H | 2 | 2 | | | - | ||
| DH | 3´2 | 1 | 3 | 2/3 | - | 4395.24 | 431.9802 |
Вычисления:
K=KQ = Kx = Kc = Kp= [(gяд1´ gэл1) ´M13/2´1/1´ [(gяд2´ gэл2) ´M23/2´2/2´ [(gяд3´ gэл3) ´M33/2´3/3´ [(gяд4´ gэл4) ´M43/2´4/4
Все прочие величины сокращаются, и получаем:
K= [(2´3´2) ¸(3´1)] ´ [3´¸(2´] 3/2 ´ { [(2/3) ¸1] ¸ [¸2] } = 4´ (0.75) 3/2 ´8/3 = (32/3) ´0.6495= 6.928
Резюме:
Это одна из простейших задач, в которой свойства равновесной смеси зависят лишь от простейших структурно-физических параметров ядер изотопов водорода.
ЗАДАЧА 8.
Рассчитать константу равновесия для реакции диссоциации молекулы CO на нейтральные атомы C и O при 2000 К: CO(газ) =C(газ) +O(газ).
Степени вырождения основных электронных состояний атомов C и O равны 9 (Термы 3P).
Значение, рассчитанное по термохимическим данным, равно 7.427×10-22 атм
Спектроскопические данные для CO приведены в табл.15.2 (Д-О, стр.467).
(Ответ в учебнике Kp= 7.790×10-22 атм).
РЕШЕНИЕ.
Таблица 1. Структурные параметры частиц. (Табл. 15.2 (Д-О, стр.467).
|
Qяд= = gяд |
Qэл= = gэл |
M, у. е. | , у. е. |
R0×1010, М |
|
|
D0, кДж/моль | |
| CO | 1 | 1 | 28 | 6.857 | 1.1282 | 2 | 2170.21 | 1072.037 |
| C | 1 | 9 | | | - | |||
| O | 1 | 9 | 16 | | - |
Полезные предварительные вычисления резко сокращают расчёты, позволяя их контролировать. Это очень хорошая школа тренировки и самоконтроля.
Масса молекулы
m(CO) = 28´10-3/6.023´1023= 4.649´10-26 кг.
Приведённая масса молекулы (для вычисления момента инерции)
(CO) = 6.857´10-3 кг /6.023´1023= 1.1385´10-26 кг.
Момент инерции молекулы
I(CO) = 1.1385´10-26 ´ (1.1282´10-10) 2 =1.449´10-46 кг´м2.
Энергия диссоциации
D0(CO) = (1072000/6.023) ´10-23 Дж =1.78´10-18 Дж.
Теплота реакции (равна энергии диссоциации) Qv = U0 = Ee
DEe(CO ® C+O) = D0(CO) = 1.78´10-18 Дж.
Тепловой "квант"
kT= 1.38´10-23´2000=2.76´10-20 Дж.
Показатель электронного фактора Больцмана
DEe(CO) / kT = 1.78´10-18 Дж/2.76´10-20 Дж = 64.5.
Фактор Больцмана
exp(-Ee(CO) / kT) = exp(-64.5) = 0.973´10-28.
Квант колебательного возбуждения
h= hc![]() = 6.62´10-34´3´1010´2170.21=19.86´10-21´2.170= 4.3096´10-20 Дж.
= 6.62´10-34´3´1010´2170.21=19.86´10-21´2.170= 4.3096´10-20 Дж.
Показатель колебательного фактора Больцмана
h/ kT=4.3096´10-20/2.76´10-20=15.61´10-1=1.561.
Колебательный фактор Больцмана
exp(-h/ kT) =exp(-1.561) = 0.21.
13) Стандартный мольный объём V0= (RT/p0) =(8.314´2000¸101325) = 0.16442.
14) Статистические суммы молекулы CO:
14.1) Поступательная
q0t (CO) = [2´p´1.38´10-23´2000´0.028¸(6.023´1023)] 3/2 ¸(6.62´10-34) 3=
= [10-46 ´486 ¸6.023] 3/2 ¸(6.62´10-34) 3== [80.69] 3/2´1033¸ [290.12] = 2.498´1033.
14.2) Вращательная
q0r (CO) = 8´p2´I ´1.38´10-23´2000/h2 =2.1792´10-18´ I/(6.62´10-34) 2 =720.
Момент инерции: I(CO) =1.138´10-26´1.273´10-20=1.448´10-46 кг´м2
14.3) Колебательная от нулевого колебательного уровня
q0v (CO) =1/{1 - exp(-h/ kT) }= 1/ (1-0.21) =1/0.79=1.265.
14.4) Электронная (отсчёт энергий нулевых уровней - от свободных атомов C и O)
q0el (CO) = 1´ exp [-E e(CO) / kT] =exp [-(-64.5)] = 0.973´10-28.
14.5) Мольная q0 (CO) = 2.498´1033´720´1.265´1028=
=2.498´720´1.265´1061=2.275´1064. .
14.6) Молекулярная статсумма CO (2-й сомножитель в Kp):
Q(CO) = 0.16442´2.275´1064/6.023´1023=6.21´1039.
15) Статистические суммы атома C:
15.1) Поступательная
q 0t (C) = [2´p´1.38´10-23´2000´0.012¸(6.023´1023)] 3/2 ¸(6.62´10-34) 3=0.700´1033.
15.2) Электроннаяq 0el (C) = gel (C, терм 3P) = 9.
15.3) Мольная q0 (C) = 0.700´1033´9 =6.300´1033.
15.4) Молекулярная статсумма атома C (3-й сомножитель в Kp):
Q(C) = 0.16442´6.300´1033/6.023´1023=1.72´109.
16) Статистические суммы атома O:
16.1) Поступательная
q0t (O) = [2´p´1.38´10-23´2000´0.012¸(6.023´1023)] 3/2 ¸(6.62´10-34) 3=1.078´1033.
16.2) Электроннаяq 0el (O) = gel (O, терм 3P) = 9.
16.3) Мольнаяq0 (O) =1.078´1033´9= 9.699´1033.
16.4) Молекулярная сумма атома O (4-й сомножитель в Kp):
Q(O) = 0.16442´9.699´1033/6.023´1023=2.647´109.
Таблица 2. Сводка статистических сумм для реакции CO(газ) =C(газ) +O(газ)
| qt0 | qr0 | qV0 | qe0 | Q0 | i | Q0 | |
| CO | 2.498´1033 | 720 | 1.265 | 0.973´10-28 | 2.275´1064 | - 1 | 6.21´1039 |
| C | 0.700´1033 | 1 | 1 | 9 = g(3P) | 6.300´1033 | +1 | 1.72´109 |
| O | 1.078´1033 | 1 | 1 | 9 = g(3P) | 9.699´1033 | +1 | 2.647´109 |
| Kp=7.33´10-22 |
17) Константа равновесия Kp (безразмерная):
Kp= [Q0(CO)] -1 ´Q0(C) ´Q0(O)
Kp = (1.72´109) ´(2.647´109) ´ [6.21´1039] -1=1.72´2.647´0.161´109´109´10-39=7.33´10-22.
Безразмерны статистические суммы и полученная константа безразмерна.
Её модуль тот же, что и у Kp, где размерностью давления является атмосфера.
Резюме:
Полученный нами результат заметно лучше того, что приведён в учебнике. Это наглядная иллюстрация больших преимуществ современной электронной вычислительной техники, тогда как в учебнике расчёты выполнялись старыми способами – по таблицам и логарифмической линейке. Отклонение от экспериментальной величины и его квадрат у нас меньше:
У нас: [(7.330-7.427) / 7.427] 2 =1.71´10-4´100%=0.017% ®|= 0.13%,
У Д-О: [(7.790-7.427) / 7.427] 2 =2.39´10-3´100%=0.239% ®|= 0.49%.
ЗАДАЧА 9. (Д-О 17.16)
Для реакции, протекающей при 698.2 К в газовой фазе
H2 (газ) + I2 (газ) =2 HI (газ)
на основании экспериментальных измерений получена константа равновесия
K698.2= [HI] * 2/([H2] * [I2] *) =54.5.
Рассчитать эту же величину статистическим методом, если DrU0o= - 9.728 кДж/моль
РЕШЕНИЕ.
Таблица 1. Структурные параметры частиц. (Табл.15.2 (Д-О, стр.467).
| M, г/моль | I´1048, кг´м2 | s |
|
|
| H2 | 2.016 | 4.59 | 2 | 4405 |
| I2 (газ) | 256 | 7430 | 2 | 214 |
| HI (газ) | 129 | 43.1 | 1 | 2309 |
1) Предварительные расчёты колебательных частот и факторов Больцмана
Тепловой "квант" равен kT=1.38´10-23´698.2=9.6352´10-21 Дж
Колебательные характеристики молекул:
H2: (H2) = c´4405=3´1010 (см/с) ´ 4405(1/см) = 1.3215´1014 (1/с)
h(H2) = 6.62´10 - 34(Дж´с) ´ 1.3215´1014 (1/с) = 8.748´10 - 20 Дж
h/kT=8.748´10 - 20 Дж/9.6352´10-21 Дж=9.08
exp(-h/kT) = exp(-9.08) =0.000114;
q0V (H2) = [1-exp(-h/kT)] -1=0.999886-1@1;
I 2: (I 2) = c´214=3´1010 (см/с) ´ 214(1/см) = 6.42´1012 (1/с)
h(I 2) = 6.62´10 - 34(Дж´с) ´ 6.42´1012 (1/с) = 4.25´10 - 21 Дж
h/kT=4.25´10 - 21 Дж/9.6352´10-21 Дж=0.441
exp(-h/kT) = exp(-0.441) =0.643;
q0V(I 2) = [1-exp(-h/kT)] -1=0.357-1@2.80;
HI: (I 2) = c´2309=3´1010 (см/с) ´ 2309 (1/см) = 6.93´1013 (1/с)
h(I 2) = 6.62´10 - 34(Дж´с) ´ 6.93´1013 (1/с) = 4.588´10 - 20 Дж
h/kT=4.588´10 - 20 Дж/9.6352´10-21 Дж=4.762
exp(-h/kT) = exp(-4.762) =0.00855;
q0V(I 2) = [1-exp(-h/kT)] -1=0.99145-1@1;
Показатель электронного сомножителя в константе равновесия:
DU0o/RT = - 9728/(8.314´698.2) = - 1.676
Сам электронный сомножитель в константе равновесия:
exp(-DU0o/RT) = exp(1.676) = 5.348
2) Константа равновесия
Число частиц за пробег реакции не изменятся Drn=0;
K=Kc=Kp= [Q0(H2)] - 1 [Q0(I2)] - 1 [Q0(HI)] 2; ®
Сокращается большинство численных коэффициентов и остаётся:
K= [M(HI) 2M(H2) - 1´M(I2) - 1] 3/2 ´ [I(HI) 2´I(H2) - 1´I(I2) - 1] ´ [s(H2) s (I2) /s (HI) 2] [´ [q0(HI)] 2´ [q0(H2)] - 1´ [q0(I2)] - 1´exp(-DU0o/RT);
Из набора молекулярных параметров играет роль множитель:
[M(HI) 2´M(H2) - 1´M(I2) - 1] 3/2´ [I(HI) 2/I(H2) ´I(I2)] ´ [s(H2) ´s (I2) /s (HI) 2] = [1292/(2.016´256)] 3/2´ [43.12/(4.597´7430)] ´(2´2/12) =0.031´18.136´4=183.1´0.0544´4=39.84.
Колебательные статистические суммы
[q0(HI)] –2 @ 1.
[q0(H2)] @1.
[q0(I2)] =2.80.
Электронный сомножитель:
exp(-DU0o/RT) = exp(1.676) = 5.348
Константа равновесия равна:
K=5.348´39.84/2.80=76.1.
Резюме:
Простота приближений и пренебрежение специфическими спиновыми эффектами ядер, приводят к выводу о том, что согласие теории и эксперимента очень хорошее. Отличие составляет всего 30%.
ЗАДАЧА 10. (Д-О 17.27)
Рассчитать статистическим методом константу равновесия и степень диссоциации H2(газ) при 3000 K и 1 атм. При этих условиях Лэнгмюр изучил протекающую в газовой фазе реакцию
H2 (газ) =2H (газ) и нашёл a=0.072. Учтите, что вследствие электронного спина основное состояние атома водорода дважды вырождено (gel=2).
РЕШЕНИЕ.
Предварительные вычисления
Тепловой "квант" kT =1.38´10-23´3000 Дж = 4.14´10-20 Дж
Стандартный мольный объём V0= (RT/p0) =(8.314´3000¸101325) = 0.2462.
m(H2) = 2´10-3/6.023´1023= 3.320´10-27 кг.
m(H) = 1´10-3/6.023´1023= 1.660´10-27 кг.
Приведённая масса молекулы (для вычисления момента инерции)
(H2) = m(H) ´m(H) / [m(H) + m(H)] = m(H) /2= m(H2) /4=0.83´10-27 кг.
Момент инерции молекулы
I(H2) = 0.83´10-27 кг´(0.7416´10-10) 2 м2 =4.565´10-48 кг´м2.
Энергия диссоциации равна DEe(H2 ® 2H) = D0(H2) = 431980.2 /6.023´1023 Дж = =7.1722´10-19 Дж (см. таблицу 1).
Показатель степени электронного фактора Больцмана
D0(H2) / kT = 7.1722´10-19 Дж/4.14´10-20 Дж =17.324
Электронный фактор Больцмана (статистическая сумма молекулы)
exp [D0(H2) / kT] = exp(17.324) = 3.3397780´107= 1/2.99421´10-8.
Квант колебательного возбуждения
h= hc![]() = 6.62´10-34´3´1010´4395.24=8.72895´10-20 Дж.
= 6.62´10-34´3´1010´4395.24=8.72895´10-20 Дж.
Показатель колебательного фактора Больцмана
h/ kT=8.72895´10-20 Дж/4.14´10-20 Дж =2.10844.
Колебательный фактор Больцмана
exp(-h/ kT) =exp(-2.10844) = 0.1214.
14) Статистические суммы молекулы H2:
14.1) Поступательная
q0t (H2) = [2´p´3.320´10-27´1.38´10-23´3000] 3/2 ¸(6.62´10-34) 3=
= (8.636´10-46) 3/2¸(6.62´10-34) 3= 25.378´10-69¸290.12´10-102=8.7474´1031
14.2) Вращательная
q0r (H2) = 8´p2´I ´1.38´10-23´3000/h2 =3.269´10-18´ I/(6.62´10-34) 2 =
=3.269´4.565´10-66/43.824´10-68 =34.05
Момент инерции: I(H2) = 4.565´10-48 кг´м2
14.3) Колебательная от нулевого колебательного уровня
q0v (H2) =1/{1 - exp(-h/ kT) }= 1/ (1-0.1214) =1/0.8786=1.1382.
14.4) Электронная (отсчёт энергий нулевых уровней - от свободных атомов H)
q0el (H2) = 1´ exp [-E e(H2) / kT] = exp [D0(H2) / kT] = exp(17.324) = 3.3398´107.
14.5) Мольная q0 (H2) = 0.2462 ´ 8.7474 ´ 1031 ´ 34.05 ´ 1.1382 ´ 3.3398´107=2.78755´1040.
14.6) Молекулярная статсумма H2 (2-й сомножитель в Kp):
Q(H2) = 2.78755´1040/6.023´1023=4.63´1016.
15) Статистические суммы атома H:
15.1) Поступательная
q 0t (H) = [2´p´1.66´10-27´1.38´10-23´3000] 3/2 ¸(6.62´10-34) 3=
=(5. 194´10-46) 3/2¸290.12´10-102= 11.837´10-69¸290.12´10-102= 4.080´1031
15.2) Электроннаяq 0el (H) = gel (H, терм 2S) = 2.
15.3) Мольная q0 (H) = 4.080´1031´2 =8.160´1031.
15.4) Молекулярная статсумма атома H (3-й сомножитель в Kp):
Q(H) = 0.2462´8.160´1031/6.023´1023=3.3336´107.
16) Константа равновесия Kp (безразмерная):
Kp= [Q0(H2)] - 1 ´ [Q0(H)] 2
Kp = [4.63´1016] -1´ (3.3336´107) 2 =1.1113´1015´ [4.63´1016] -1=0.02400
17) Степень диссоциации определяется следующими выражениями:
H2 = 2H·®М атериальный баланс в следующей строке:
(1-a) ´p0 2a´ p0®Далее две равновесные мольные доли
a) X*(H2) =(1-a) /(1+a),
b) X*(H) = 2a/(1+a).
Равновесные парциальные давления – доли от общего равновесного давления:
d) p*(H2) = [(1-a) /(1+a)] ´p*,
e) p*(H·) = [2a/(1+a)] ´p*.
По условию задачи общее давление 1 атм.
®Константа равновесия равна:
Kp = [2a/(1+a)] 2/ [(1-a) /(1+a)] =4a2/(1-a2) = 0.024.
Получилось уравнение: 4a2/(1-a2) = 0.024.
А) РЕШЕНИЕ: 4.024´a2 = 0.024; ® a = 0.0772.
ЗАДАЧА 11. (Д-О 17.28)
Рассчитать константу равновесия при 298 К для реакции.
H2 (газ) + D2 (газ) =2HD (газ)
Недостающие частоты валентных колебаний найти, пользуясь приближением гармонического осциллятора. Считать силовые константы и межатомные расстояния одинаковыми.
РЕШЕНИЕ.
Предварительные вычисления
Все силовые константы одинаковы (w2) = (w2) = (w2) =const, и отсюда следует
Пропорция частот колебаний связей:
n(HD): n(H2): n(D2) = (HD) - ½: (H2) - ½: (D2) - ½ =
= [ (H2) / (HD)] ½: 1: [(H2) / (D2)] ½ = (3/4) ½: 1: (1/2) ½ = 0.866: 1: 0.707
n(HD): n(H2): n(D2) =0.866: 1: 0.707
Отсюда определяются волновые числа колебаний:
n(H2) = 4405 см-1
n(HD) = 4405´0.866=3815 см-1
n(D2) = 4405´0.707 =3114 см-1
Далее получаются собственные частоты колебаний:
n0(H2) = 3´1010´4405 с-1=1.3215´1014 с-1
n0(HD) =3´1010´3815 с-1=1.1445´1014 с-1
n0(D2) = 3´1010´3114 с-1=9.342´1013 с-1
Колебательные кванты:
hn0(H2) =6.62´10-34 Дж´с ´ 1.3215´1014 с-1 =8.748´10-20 Дж
hn0(HD) =6.62´10-34´1.1445´1014 с-1 =7.577´10-20 Дж
hn0(D2) = 6.62´10-34´9.342´1013 с-1 =6.1844´10-20 Дж
Тепловой "квант" kT =1.38´10-23´298 Дж =4.112´10-21 Дж
Показатели больцмановских факторов для колебаний:
hn0(H2) / kT =8.748´10-20 Дж/4.112´10-21 Дж=21.27
hn0(HD) / kT =7.577´10-20 Дж/4.112´10-21 Дж=18.43
hn0(D2) / kT =6.1844´10-20 Дж/4.112´10-21 Дж=15.04
Все hn0 >> kT
Больцмановские факторы для колебаний практически нулевые:
exp(-21.27) @0
exp(-18.43) @0
exp(-15.04) @0
Колебательные статистические суммы все равны 1:
qV 0(HD) = [1-exp(-hn0(HD) / kT)] @1
qV 0(H2) = [1-exp(-hn0(H2) / kT)] @1
qV 0(D 2) = [1-exp(-hn0(D2) / kT)] @1
Колебательные суммы состояний равны 1 с большой точностью.
Приращение нулевой энергии (теплота реакции при T=0 K)
DrUo=(1/2NA) [2h0HD h0H2 h0D2] ;
DrUo =0.5´6.023´1023´ [2´7.577-8.748-6.1844] ´10-20=3.0125´220=662.75 Дж.
Показатель фактора Больцмана для приращения нулевой энергии:
DrUo/ RT =662.75 Дж /(8.314´298) Дж=0.268
Фактор Больцмана для приращения нулевой энергии:
exp(-DrUo/ RT) = exp(-0.268) = 0.765
Константа равновесия
K= [M(HD) 2´M(H2) - 1´M(D2) - 1] 3/2´ [I(HD) 2´I(H2) - 1´I(D2) - 1] ´ [s(H2) ´s (D2)] [´[qV 0 (HD)] 2 ´ [qV 0(H2)] - 1´ [qV 0(D2)] - 1 ´ exp(-DrUo/ RT) = [M(HD) 2M(H2) - 1´M(D2) - 1] 3/2´ [(HD) 2´(H2) - 1´(D2) - 1] ´ [2´2] ´exp(-DrUo/ RT)
K= [M(HD) 2´M(H2) - 1´M(D2) - 1] 3/2´ [ (HD) 2´ (H2) - 1´(D2) - 1] ´ [2´2] ´exp(-DrUo/ RT) =
K= [(1+2) 2 ´(1/2) ´ (1/4)] 3/2 ´ [(2/3) 2´2´1] ´ [2´2] ´ 0.765=
K= (9/8) 3/2´ (8/9) ´ 4´0.765=(9/8) 1/2´4´0.765=3.246
Резюме:
В этой задаче колебательные статистические суммы не играют роли. Они все равны 1. Из-за равенства структурных параметров играют роль лишь энергии остаточных колебаний, а также лишь отношения масс, приведённых масс молекул, а также чисел симметрии.
ЗАДАЧА 12.
Рассчитать константу равновесия для реакции газообразного водорода с газообразным тритием.
H2 (газ) + T2 (газ) =2HT (газ)
Недостающие частоты валентных колебаний найти, пользуясь приближением гармонического осциллятора. Считать силовые константы и межатомные расстояния одинаковыми.
ПРИМЕЧАНИЕ: Эта задача полностью подобна предыдущей.