Статья: Об особенностях развития вынужденной эластической деформации при растяжении стеклообразного полиэтилентерефталата в адсорбционно-активной среде
Об особенностях развития вынужденной эластической деформации при растяжении стеклообразного полиэтилентерефталата в адсорбционно-активной среде
Способность полимеров к вынужденной эластической деформации является их фундаментальным свойством и лежит в основе важнейшего технологического приема, используемого при изготовлении пленок и волокон,— ориентационной вытяжки. В связи с этим холодная вытяжка полимеров служила предметом многочисленных исследований, и в настоящее время она хорошо описана и изучена [1, 2]. Тем не менее, некоторые аспекты этого явления до сих пор остаются неясными, и в первую очередь это касается взаимосвязи между характером кривой растяжения полимера и его структурными перестройками, происходящими в процессе деформирования.
Еще в меньшей степени изучено влияние жидких сред на процесс развития неупругой деформации полимера. В последние годы было установлено, что холодная вытяжка полимеров в жидких адсорбционно-активных средах в структурном плане резко отличается от холодной вытяжки полимера на воздухе [3]. Это отличие легко наблюдать даже визуально. Вместо хорошо известного явления возникновения и распространения по образцу шейки, в адсорбционно-активной среде на первых этапах деформирования не происходит заметного сужения образца, а переход полимера в ориентированное состояние осуществляется внутри большого количества специфических микротрещин, покрывающих всю рабочую часть образца [4].
Особенности зарождения и роста таких микротрещин в этом случае определяют механическое поведение полимера в целом. Значительное число исследований посвящено вопросам возникновения и роста микротрещин, однако лишь в некоторых работах [5—9] сделаны попытки найти взаимосвязь между особенностями роста микротрещин и механическим поведением полимера.
В данной работе приведены результаты исследования процессов возникновения и роста микротрещин при деформировании ПЭТФ в адсорбционно-активной среде с использованием прямых методов исследования — кино- и фотосъемки и сопоставлены полученные данные с макроскопическими механическими свойствами полимера в тех же условиях.
Впервые мысль о взаимосвязи кривой растяжения полимеров с его макроскопическими структурными перестройками была высказана в работах Лазуркина [1]. Визуальные наблюдения образования и роста шейки в полимерах позволили заключить, что «в области спада напряжения происходит формирование шейки. Сечение ее уменьшается, за счет этого возрастает длина. К концу спада напряжения формирование шейки заканчивается и начинается ее рост в длину за счет соседних, мало продеформированных частей образца» [1]. Другими словами, на первом этапе растяжения полимера (в интервале деформаций от предела вынужденной эластичности до выхода кривой растяжения на плато) происходит формирование сравнительно узкой зоны пластически деформированного полимера и ее прорастание через все поперечное сечение испытываемого образца. Дальнейшая деформация осуществляется путем распространения сформировавшейся узкой зоны, называемой шейкой, на всю рабочую часть образца. Как видно, уже в работах Лазуркина имелась возможность изучать скорость распространения зоны пластической деформации полимера, используя кривые растяжения.
Позднее было установлено, что процесс холодной вытяжки полимера в адсорбционно-активной среде, несмотря на отмеченные выше отличия, имеет много общего с хорошо изученным процессом деформации полимера на воздухе [9]. Хотя при растяжении полимера в адсорбционно-активной среде не происходит образования монолитной шейки, пластическая деформация полимера на первых этапах растяжения осуществляется в области вершин специфических микротрещин, прорастающих (так же, как и шейка) через поперечное сечение деформируемого полимера. Такая аналогия позволила определить скорость роста микротрещин или, что то же, скорость распространения зоны пластической деформации в полимере при его растяжении в адсорбционно-активной среде. Действительно, поскольку к моменту выхода динамометрической кривой в область стационарного напряжения большая часть микротрещин успевает прорасти через все поперечное сечение образца, то, фиксируя время выхода динамометрической кривой на плато и зная размеры образца, можно определить некоторую скорость роста микротрещин. Было показано, что скорость роста микротрещин зависит от вязкости и поверхностной активности жидкой среды, а также определяется условиями нагружения полимера [12].
Тем не менее, необходимо отметить, что многочисленные экспериментальные данные по зависимости числа микротрещин, возникающих при деформировании полимера в адсорбционно-активной среде, от степени вытяжки, полученные с помощью световой микроскопии [9] и положенные в основу описанного выше метода определения скорости роста микротрещин из кривых растяжения, являются весьма приблизительными. Эти данные были получены при периодической остановке процесса растяжения полимера; их сопоставляли с деформационными кривыми, полученными в условиях растяжения полимера с постоянной скоростью. В связи с этим в данной работе использовали прибор, с помощью которого можно следить за числом микротрещин и их линейными размерами непосредственно при деформировании полимера в адсорбционно-активной среде с постоянной скоростью, что позволяет корректно сравнить данные структурного исследования и динамометрии.
Прежде всего, следует отметить прямо пропорциональную зависимость длины микротрещин от времени деформирования полимера, т. е. в исследованном интервале скоростей деформирования микротрещины в ПЭТФ растут с постоянной скоростью (рис. 1).
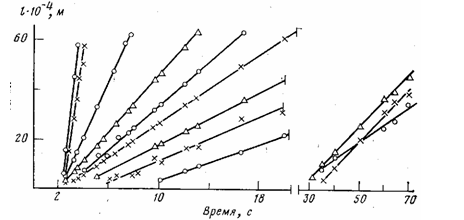
Рис. 1. Типичная картина зависимости длины отдельных микротрещин от времени деформирования ПЭТФ при скорости деформирования 1,67-10-4 м/с
Другая важная особенность полученных данных — значительное различие в скоростях роста отдельных микротрещин. Оказывается, что при деформировании полимера в адсорбционно-активной среде скорость роста микротрещин в зависимости от степени деформации не является постоянной и различия в скоростях роста отдельных микротрещин в одном и том же образце могут достигать значительных величин.
Этот результат позволяет сделать важный вывод о том, что значения скорости роста микротрещин, определяемые из кривых растяжения [12],— некие усредненные величины. Были измерены скорости роста большого числа индивидуальных микротрещин (не менее 200 для каждых условий деформирования), и после статистической обработки эти данные были представлены в виде соответствующих кривых распределения.
На рис. 2 представлены кривые распределений микротрещин по линейным скоростям роста для трех скоростей деформирования. Как видно, кривые распределения асимметричны по форме и имеют четко выраженный максимум, соответствующий наиболее вероятной линейной скорости роста микротрещин.
Хорошо видно, что увеличение скорости деформирования от 8,33 • 10~6 до 1,67-Ю-4 м/с приводит к расширению распределения в область более высоких скоростей.
Полученные результаты представляются весьма важными, поскольку они позволяют получить информацию не только о характере деформации полимера в адсорбционно-активной среде, но и о структуре деформированного полимера.
Действительно, полученные данные подтверждают важную роль микродефектности полимера в его механическом поведении [9, 13]. Проявлением такой неоднородности является, в частности, возникновение шейки в деформируемом полимере в каком-либо одном, самом «опасном» месте.
Наличие распределения скоростей роста микротрещин в деформируемом полимере свидетельствует о существовании в материале набора микродефектов, создающих набор концентраторов напряжения, инициирующих локализованную пластическую деформацию. Эти концентраторы напряжения различаются по «опасности» и вовлекаются в процесс инициирования локализованной пластической деформации, т. е. в процесс зарождения микротрещин при различных уровнях напряжения, запасенных образцом.
В силу замедленности релаксационных процессов, протекающих в стеклообразных полимерах, уровень запасаемых полимером напряжений легко изменять, меняя скорость его деформации.
Как видно из рис. 2, при этом не только возрастает наиболее вероятная линейная скорость роста микротрещин, но и заметно расширяется их распределение, что свидетельствует о вовлечении в процесс деформации множества новых концентраторов напряжения.
Об этом же свидетельствуют данные о количестве микротрещин, возникающих в полимере при различных
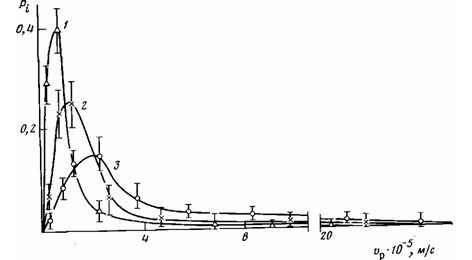
Рис. 2. Кривые распределения микротрещин по линейным скоростям роста при деформировании ПЭТФ в этиловом спирте со скоростью 8,33-10~6 (1), 3,33-10-5 (2) и 1,67-10-4 м/с (3)
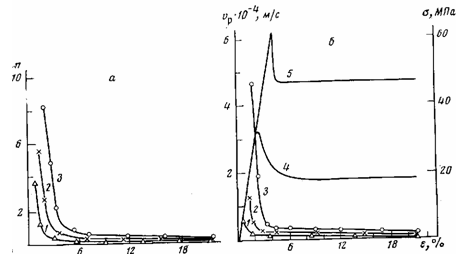
Рис. 3. Зависимость числа возникающих микротрещин п (а), их линейной скорости роста и напряжения (б) от величины деформации при растяжении ПЭТФ в этиловом спирте со скоростью 8,3310-6 (1); З.ЗЗ-10-5 (2); 1,67-10~4 (3); 1,5810-' (4) и на воздухе со скоростью 1,58-10-4 м/с (5)
скоростях его деформирования в адсорбционно-активной среде (рис. 3, а). Хорошо видно, что при всех исследованных значениях деформации большее количество микротрещин возникает в образцах, растягиваемых с большей скоростью, т. е. в условиях, при которых образец находится при более высоком напряжении. Именно это обстоятельство позволяет вовлечь в процесс деформации часть концентраторов напряжения, «безопасных» при меньших скоростях деформации и поэтому неспособных в этих условиях инициировать рождение микротрещины. Более того, уменьшая скорость растяжения в адсорбционно-активной среде, можно достичь условий, при которых в полимере на самом «опасном» дефекте будет зарождаться всего лишь одна микротрещина и макроскопически процесс деформации полимера будет аналогичен его деформации на воздухе [14]. Основное отличие в этом случае будет заключаться в структуре полимера, перешедшего в ориентированное состояние, однако этот вопрос мы не рассматривали в данной работе.
Итак, наличие распределения микротрещин по скоростям роста связано в первую очередь с набором микродефектов или микронеоднородностей в полимере. Однако следует учитывать и тот факт, что прорастание первых микротрещин через все поперечное сечение образца так же, как прорастание шейки, приводит к падению напряжения и, следовательно, скорость роста последующих микротрещин будет ниже, так как они возникли при меньшем уровне напряжений. Таким образом, распределение микротрещин по скоростям роста зависит от микродефектности и микронеоднородности образца, а также от релаксации напряжений, связанной с развитием микротрещин.
На рис. 3, б представлена зависимость скорости роста микротрещин от степени растяжения полимера для трех скоростей его деформации в ад-сорбционно-активной среде. На этом же рисунке для сравнения приведена кривая растяжения ПЭТФ в этиловом спирте. Анализ данных, представленных на рис. 3, позволяет нам качественно связать вид кривой растяжения полимера с числом и скоростями роста возникающих в нем микротрещин. Наибольшее число микротрещин возникает при малых деформациях, которые лежат в области напряжений до достижения макроскопического предела вынужденной эластичности. Микротрещины, возникающие на начальном участке, растут с наибольшей скоростью. Оказывается, что как только быстрорастущие микротрещины прорастут через все поперечное сечение образца, напряжение падает; это ведет к резкому уменьшению числа возникающих микротрещин и скорости их роста. Другими словами, механическое поведение ПЭТФ в области спада напряжения вплоть до выхода кривой растяжения на прямолинейный участок обусловлено сложными процессами возникновения и поперечного роста микротрещин. Форма кривой растяжения полимера в адсорбционно-активной среде содержит информацию об описанных выше процессах, а сама кривая растяжения может служить тонким инструментом исследования механизма деформации.
Сравнение динамометрических кривых растяжения ПЭТФ на воздухе и в адсорбционно-активной среде (рис. 3, б) показывает, что деформирование в адсорбционно-активной среде приводит к снижению механических характеристик полимера, как это было показано в работах [15, 16], кроме того, имеется различие в спаде напряжения после достижения предела вынужденной эластичности. На наш взгляд, это различие обусловлено тем, что на воздухе прорастание шейки происходит, как правило, в одном месте образца, в связи, с чем на динамометрической кривой растяжения обычно возникает достаточно резкий спад напряжения. В то же время множество растущих с различными скоростями микротрещин, естественно, сложным образом «разгружают» растягиваемый полимер, тем более что микротрещины могут рождаться и расти во всей исследованной области растяжения (до 50%) и вносить свой вклад в спад напряжения. Этот вывод подтверждают и данные работы [14], в которой было обнаружено, что в тех случаях, когда при малых скоростях деформирования полимера в адсорбционно-активной среде в образце возникает и растет всего лишь одна микротрещина, спад напряжения на динамометрической кривой растяжения после достижения предела вынужденной эластичности становится таким же резким, как и при деформации полимера на воздухе.
Сопоставим теперь полученные нами из распределений по скоростям наиболее вероятные линейные скорости роста микротрещин с некоторой средней скоростью роста микротрещин, определяемой из кривых растяжения по методу, описанному в работе [12].
На рис. 4, а совместно представлены данные по определению скоростей роста микротрещин, полученные с помощью кинофотосъемки и кривых растяжения от логарифма скорости деформирования. При малых скоростях деформирования, когда число возникающих микротрещин невелико, наблюдается удовлетворительное совпадение наиболее вероятной линейной скорости роста микротрещин, определяемой по значению максимума на кривой распределения (рис. 2), и средней скорости роста, определяемой из кривой растяжения. Однако при деформировании со скоростью растяжения 1,58-Ю-4 м/с, когда резко увеличивается число возникающих микротрещин, как это видно на рис. 4, б, средняя скорость роста микротрещин, определенная из динамометрической кривой растяжения, становится значительно больше соответствующей величины, полученной из прямых микроскопических наблюдений.
Проведенное сопоставление свидетельствует о том, что величина средней скорости роста микротрещин, получаемая из кривой растяжения, удовлетворительно соответствует реальной наиболее вероятной скорости роста микротрещин только в области невысоких скоростей деформации, где, как видно из рис. 4, б, количество возникающих микротрещин относительно невелико. При повышенных скоростях растяжения общее количество возникающих микротрещин резко возрастает (рис. 4, б), что, в свою очередь, усложняет картину релаксации напряжения в полимере. Однако очевидно, что наибольшее влияние в этом процессе оказывают наиболее быстро прорастающие микротрещины; хотя их относительное число невелико, они вносят главный вклад в релаксацию напряжения полимера, в связи с чем и наблюдается столь сильное различие между данными, получаемыми из механических испытаний и из микроскопических наблюдений.
Таким образом, представленные данные свидетельствуют о глубокой и сложной взаимосвязи между механическим поведением полимера, деформируемого в адсорбционно-активной среде, и процессами возникновения и роста специфических микротрещин, а также микродефектностью и структурной неоднородностью стеклообразных полимеров.
ЛИТЕРАТУРА
1. Лазуркин Ю. С. Дис. на соискание уч. ст. докт. физ.-мат. наук, М.: Ин-т физ. проблем АН СССР, 1954.
2. Уорд И. Механические свойства твердых полимеров. М.: Химия, 1975, с. 247.
3. Kambour R. P. Macromolec. Rev., 1973, v. 7, p. 1.
4. Волынский А. Л., Вакеев Н. Ф.// Высокомолек. соед. А, 1975, т. 17, № 7, с. 1610.
5. Brown N. Phil. Mag., 1975, v. 32, № 5, p. 1041.
6. Brown N.. Fischer S. J. Polymer Sci. Polymer Phys. Ed., 1975, v. 13, JNs 7, p. 1315.
7. Brown N. In: Proceeding II International Conference Mechanical Behaviour Materials. Boston: Mass., 1976, p. 1530.
8. Brown N., Mertzger B. J. Polymer Sci. Polymer Phys. Ed., 1980, v. 17, № 9, p. 1979.
9. Алескеров А. Г., Волынский А. Л., Вакеев H. Ф. Высокомолек. соед., Б, 1977, т. 19, № 3, с. 218.
10. Пазухина Л. Ю., Ярышева Л. М., Сточес Р. Н., Бакеев Н. Ф., Козлов П. В. Метод определения линейной скорости роста микротрещин с построением кривых распределения при деформировании полимеров в жидких средах.— Высокомолек. соед. А, 1982, т. 24, № 8, с.
11. Волынский А. Л., Смирнов В. Д., Сточес P. Н., Герасимов В. И.,
12. Алескеров А. Г., Бакеев Н. Ф. Высокомолек. соед. А, 1976, т. 18, № 4, с. 940.
13. Волынский А. Л., Шитов Н. А., Вакеев Н. Ф. Высокомолек. соед. А, 1981, № 5, 978.