Контрольная работа: Розв'язання рівнянь методом оберненої матриці та методом Гауса
Контрольна робота
З дисциплiни: Вища математика
За темою (роздiлом навчального плану)
Прізвище,ім’я, по батькові студента
Данiщук Мирослава Евгенiївна
Прiзвище та інiцiали викладача
Дюженкова Ольга Юріївна
Київ 2008 рiк.
Завдання 1
Систему рівнянь записати в матричній формі та розв’язати методом оберненої матриці та методом Гауса.
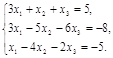 (*)
(*)
Розв’язання.
Запишемо дану систему рівнянь (*) в матричній формі:
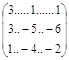
![]() =
= ![]() . (1)
. (1)
Введемо позначення:
А≡ 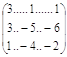 - матриця системи,
- матриця системи,
Х ≡ ![]() - вектор-стовпець з
невідомих членів,
- вектор-стовпець з
невідомих членів,
В ≡ ![]() - вектор-стовпець з
вільних членів.
- вектор-стовпець з
вільних членів.
1) Розв’яжемо систему рівнянь (*) методом оберненої матриці.
Домноживши рівність (1) зліва на обернену матрицю A-1 одержимо:
![]()
Знайдемо обернену матрицю до даної:
A-1 =
![]()
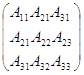 ,
,
де А11=
(-1) 2·![]() =10-24=-14,А12=
(-1) 3·
=10-24=-14,А12=
(-1) 3·![]() =- (-6+6)
=0,А13= (-
=- (-6+6)
=0,А13= (-
1) 4·![]() =-12+5=-7,А21= (-1)
3·
=-12+5=-7,А21= (-1)
3·![]() =- (-2+4) =-2,А22=
(-1) 4
=- (-2+4) =-2,А22=
(-1) 4
·![]() =-6-1=-7,А23= (-1)
5·
=-6-1=-7,А23= (-1)
5·![]() =- (-12-1) =13,А31=
(-1) 4·
=- (-12-1) =13,А31=
(-1) 4·![]() =-
=-
6+5=-1,А32=
(-1) 5·![]() =- (-18-3)
=21,А33= (-1) 6·
=- (-18-3)
=21,А33= (-1) 6·![]() =-15-3=-18.
=-15-3=-18.
det A = 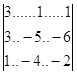 = 30-6-12+5+6-72=-49.
= 30-6-12+5+6-72=-49.
Тому
A-1 =
![]()
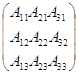 =
-
=
- 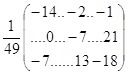 .
.
Отже, розв’язок даної системи в матричній формі запишеться так:
X = - 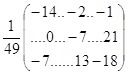 ·
·![]() =-
=-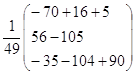 =
=
=-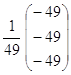 =
=![]() .
.
Тобто х1=1,х2=1,х3=1.
2) Розв’яжемо систему рівнянь методом Гауса.
Метод Гауса полягає в послідовному виключенні невідомих за допомогою елементарних перетворень.
Спочатку виключимо х1 з другого та третього рівнянь системи (*).
Помножимо друге рівняння системи (*) на - 1 і додамо його до першого - запишемо замість другого рівняння,
Помножимо третє рівняння на - 3 і додамо його до першого - запишемо замість третього рівняння:
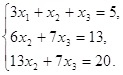 (2)
(2)
Тепер виключимо х3 з третього рівняння отриманої системи (2). Для цього помножимо третє рівняння системи (2) на - 1 і додамо до другого - запишемо замість третього рівняння системи:
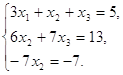 (3)
(3)
З рівняння (3) маємо:
х2= 1,х2
=![]() = 1,х3 =
5-3·1-1=1.
= 1,х3 =
5-3·1-1=1.
Відповідь. дана система в матричній формі:
![]()
![]()
![]()
![]() =
= ![]() ,
,
її розв’язок (1; 1;1).
Завдання 2
Показати, що перші
три вектори ![]() ,
, ![]() ,
, ![]() утворюють базис
тривимірного векторного простору, і розкласти вектор
утворюють базис
тривимірного векторного простору, і розкласти вектор ![]() за цим базисом (при
розв’язанні системи лінійних рівнянь використати формули Крамера):
за цим базисом (при
розв’язанні системи лінійних рівнянь використати формули Крамера):
![]() = (1,2,3),
= (1,2,3), ![]() = (2,2,3),
= (2,2,3), ![]() = (1,1,1),
= (1,1,1), ![]() = (5,7,10)
= (5,7,10)
Розв’язання.
Для того, щоб
вектори ![]() ,
, ![]() ,
, ![]() утворювали базис,
необхідно щоб вони були лінійно незалежними. Тобто має виконуватись рівність:
утворювали базис,
необхідно щоб вони були лінійно незалежними. Тобто має виконуватись рівність:
α ![]() +β
+β ![]() +γ
+γ ![]() = 0,за умови, що α =
β = γ = 0.
= 0,за умови, що α =
β = γ = 0.
Тобто
α ![]() +β
+β ![]() +γ
+γ ![]() = 0,
= 0,
або
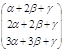 =
= ![]() .
.
Тоді, система:
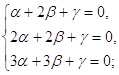
повинна мати тільки нульове рішення. Це можливо тільки, якщо її визначник не дорівнює нулю.
Визначник системи:
А = ![]()
![]()
![]() , det A =
1*2*1+2*1*3+2*3*1-3*2*1-2*2*1-3*1*1=1
, det A =
1*2*1+2*1*3+2*3*1-3*2*1-2*2*1-3*1*1=1![]() 0.
0.
Отже, вектори ![]() ,
, ![]() ,
, ![]() утворюють базис
тривимірного векторного простору.
утворюють базис
тривимірного векторного простору.
Тоді вектор ![]() є їх лінійною комбінацією:
є їх лінійною комбінацією:
![]() = b1
= b1![]() + b2
+ b2 ![]() + b3
+ b3 ![]() .
.
Числа b1,
b2, b3 будуть координатами вектора у базисі ![]() ,
, ![]() ,
, ![]() . Знайдемо їх, розв’язавши
відповідну систему:
. Знайдемо їх, розв’язавши
відповідну систему:
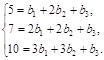
Систему лінійних рівнянь розв’яжемо, використовуючи формули Крамера:
b1 = ![]() ,
,
b2 =![]()
b3 = ![]() .
.
![]() = det
= det![]()
![]()
![]() =
5*2*1+2*1*10+7*3*1-10*2*1-7*2*1-3*1*5 = 2,
=
5*2*1+2*1*10+7*3*1-10*2*1-7*2*1-3*1*5 = 2,![]() =
det
=
det ![]()
![]()
![]() =
1*7*1+5*1*3+2*10*1-3*7*1-5*2*1-10*1*1 = 1,
=
1*7*1+5*1*3+2*10*1-3*7*1-5*2*1-10*1*1 = 1,![]() =
det
=
det ![]()
![]()
![]() =1*2*10+2*7*3+2*3*5-3*2*5-2*2*10-3*7*1
= 1.
=1*2*10+2*7*3+2*3*5-3*2*5-2*2*10-3*7*1
= 1.
Тоді b1 = 2,b2 = 1,b3 = 1.
Отримали вектор ![]() у базисі
у базисі ![]() ,
, ![]() ,
, ![]() :
: ![]() = 2
= 2![]() +
+ ![]() +
+ ![]() .
.
Відповідь. вектори ![]() ,
, ![]() ,
, ![]() утворюють базис
тривимірного векторного простору,
утворюють базис
тривимірного векторного простору, ![]() = 2
= 2![]() +
+ ![]() +
+ ![]() .
.
Завдання 3
Задано: координати трьох точок А, В, С. Записати рівняння сторін трикутника АВ, АС і ВС, висоти АК, знайти кут А і координати точки К.
A (0;
2), B (2;
3), С (1;
3).
Розв’язання.
рівняння АВ:
![]() ,
,
звідси рівняння прямої АВ: х - 2у + 4=0;
рівняння АС:
![]() ,
,
звідси рівняння прямої АС: х - у +2=0;
рівняння ВС:
![]() ,
,
звідси рівняння прямої ВС: у = 3.
2) З урахуванням
перпендикулярності прямої ВС і висоти АK нормальний вектор прямої ВС є
напрямним прямої АК: ![]() (0;
(0;
1) - нормальний
вектор прямої ВС, ![]() (0;
(0;
1) - напрямний вектор прямої АК. Напишемо рівняння цієї прямої, враховуючи, що їй належить т. А (0;
2) -
![]()
![]() =0
=0
х = 0 - рівняння прямої АК.
3) кут А - гострий кут між прямими АВ і АС:
∟A = ∟BAK - ∟CAK,
де ∟BAK =
arctg (BK / AK) = arсtg (2/1) = arсtg 2,∟CAK=arctg (CK / AK) = arctg (1/1)
= ![]() ,
,
тому ∟ A =
arctg 2 - ![]() .
.
4) Знайдемо точку К - точку перетину висоти АК і прямої ВС, тобто координати т. К є розв’язком системи рівнянь даних прямих:
![]()
Маємо: К (0;
3).
Відповідь. (АВ): х - 2у + 4=0, (АС): х - у +2=0;
(ВС): у = 3;
(АК): х=0;
∟ A = arctg
2 - ![]() ;
;
К (0;3).
Завдання 4
Знайти границі функцій (не використовуючи правило Лопіталя):
а) ![]() ;
;
б) ![]() ;
;
в) ![]()
Розв’язання:
а) Коли x прямує до нескінченності, молодшими степенями x можна нехтувати:
![]() =
= ![]() =
=![]() =-3;
=-3;
б) Здійснимо заміну змінних y = x - 2:
![]() =
=![]() = -
= - ![]() ,
,
розпишемо синус за допомогою формули Тейлора:
sin у = y - ![]() +…
+…
Тоді:
![]() = -
= - 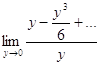 = -
= - ![]() = -
= - ![]() 1 -
1 - ![]() (-
(-![]() ) +…=-1+0+…=-1;
) +…=-1+0+…=-1;
в) Скористаємося визначенням числа e:
е = 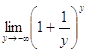
і здійснимо заміну змінних y = - 2x - 1:
![]() =
= 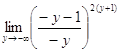 =
= ![]()
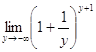
![]()
![]() =
=
=
=
![]()
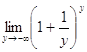
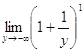
![]()
![]() =
= ![]()
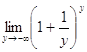
![]()
![]() =
е2.
=
е2.
Відповідь. - 3; - 1; е2.
Завдання 5
Знайти похідну функції:
у = еsin x ln x
Розв’язання.
Скористаємося формулою диференціювання добутку і складної функції:
![]() .
.
Відповідь. ![]() .
.
Завдання 5
Дослідити функцію методами диференціального числення і побудувати її графік. Досліджувати функцію рекомендується за такою схемою:
1) знайти область визначення й область зміни функції;
2) дослідити функцію на неперервність, знайти точки розриву функції (якщо вони існують) і точки перетину її графіка з осями координат;
3) знайти інтервали зростання і спадання функції і точки її локального екстремуму;
4) знайти інтервали опуклості й угнутості графіка функції та точки перегину;
5) знайти асимптоти графіка функції.
у = ![]() .
.
Розв’язання.
1) Область визначення - вся числова вісь за винятком x = - 3 и x = +3, коли знаменник перетворюється в нуль:
х є (-∞; - 3) U (-3; +3) U (+3; +∞),
область значень функції - вся числова вісь за виключенням y = 0: у є (-∞; 0) U (0; +∞).
2) Точки розриву x = - 3 и x = +3, коли знаменник перетворюється в нуль;
функція перетинає
вісь y при х = 0, у = - ![]() .
.
3) Інтервали зростання і спадання функції і точки її локального екстремуму:
знайдемо похідну функції:
![]() ,
,
похідна додатна при x < 0, тому функція при x <0 зростає,
похідна від’ємна при x > 0, тому функція при x > 0 спадає,
похідна дорівнює 0 при x = 0, тому функція при x = 0 досягає локального екстремуму;
знайдемо другу похідну функції:
![]() ,
,
друга похідна
дорівнює - ![]() при x = 0, тобто від’ємна,
тому даний локальний екстремум - це локальний максимум.
при x = 0, тобто від’ємна,
тому даний локальний екстремум - це локальний максимум.
4) Знайдемо інтервали опуклості й угнутості графіка функції та точки перегину:
друга похідна додатна в інтервалах (-∞; - 3), (+3; +∞), тому в них функція випукла вниз;
друга похідна від’ємна в інтервалі (-3; +3), тому в ньому функція випукла вгору;
відповідно, точки x = - 3 и x = +3 - точки перегину
5) Знайдемо асимптоти графіка функції:
при х→-∞ і х→+∞ функція прямує до нуля, тому пряма y = 0 - горизонтальна асимптота;
точки x = - 3 и x = +3, коли знаменник перетворюється в нуль, визначає дві вертикальні асимптоти.
6) Побудуємо графік функції:
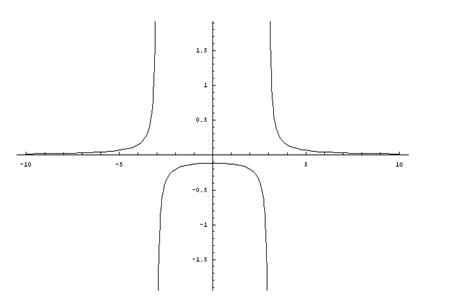
Відповідь.1) х є (-∞; - 3) U (-3; +3) U (+3; +∞), у є (-∞; 0) U (0; +∞);
2) точки розриву x = - 3 и x = +3;
функція
перетинає вісь в т. (0; - ![]() );
);
3) функція при x <0 зростає,
функція при x > 0 спадає,
функція при x = 0 досягає локального екстремуму;
у=-![]() при x = 0 - локальний
максимум;
при x = 0 - локальний
максимум;
4) в інтервалах (-∞; - 3), (+3; +∞) функція випукла вниз;
в інтервалі (-3; +3) функція випукла вгору;
точки x = - 3 и x = +3 - точки перегину;
5) y = 0 - горизонтальна асимптота;
x = - 3 и x = +3 - вертикальні асимптоти.
Завдання 6
Знайти невизначені інтеграли:
а) ![]() , б)
, б) ![]() .
.
Розв’язання.
а) Здійснимо заміну змінних y = cos x - 4, dy = - sin x dx:
![]() ;
;
б) Скористаємося формулою інтегрування за частинами:
![]() =
=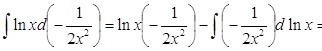
=-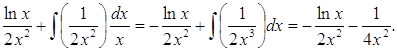
Відповідь. ![]() ;
; ![]() .
.
Завдання 7
Знайти частинні похідні за обома змінними функції двох змінних:
z (x,y) =x ln y
+ y ![]()
Розв’язання.
Скористаємося формулою диференціювання і складної функції:
![]() ,
,
![]()
Відповідь. ![]() ;
; ![]() .
.
| Методичний матеріал по викладанню алгебри | |
|
ЗМІСТ Урок - 1. Поняття про вектори. Абсолютна величина вектора і напрям Урок - 2. Рівність векторів. Розв"язування вправ Урок - 3. Координати вектора ... x'=x+a, y'=y+b ] 2) на цій пів прямій будуємо точку С, яку одержимо суміщенням з точкою В (існує паралельне перенесення, при якому початок вектора АВ переходить у точку D, а кінець точки В точку С ... |
Раздел: Рефераты по педагогике Тип: учебное пособие |
| Формування в учнів умінь розв"язувати задачі на рух | |
|
Зміст Вступ 1. Теоретичні основи розв"язування задач на рух 1.1 Роль задач у початковому курсі математики 1.2 Місце задач на рух у системі складених ... Далі вчитель ще раз аналізує другий спосіб розв'язання. Тому на малюнку не випадково другий і третій прапорці на кожній прямій розміщені строго один під одним. |
Раздел: Рефераты по педагогике Тип: дипломная работа |
| Метод векторів та його застосування | |
|
Метод векторів та його застосування Вступ Поняття вектора є одним із фундаментальних понять сучасної математики. Його можна визначити по-різному: як ... Нехай (, , ) деякий базис простору , - довільний вектор цього простору. Розв"язання: нехай O - центр маси вантажу, до якого прикладено силу P. Розкладемо вектор за двома взаємно перпендикулярними напрямами, як показано на малюнку. |
Раздел: Рефераты по математике Тип: курсовая работа |
| Методи розв"язування одновимірних та багатовимірних нелінійних ... | |
|
Міністерство освіти і науки України Полтавський національний технічний університет імені Юрія Кондратюка Факультет інформаційно-телекомунікаційних ... 3. Розв"язання задачі мінімізації за допомогою методу Ньютона і методу найшвидшого спуску double eps,x,y,N=-1,kk=1.0; |
Раздел: Рефераты по математике Тип: курсовая работа |
| Евклідова і неевклідова геометрії | |
|
Зміст Введення Глава I. Розвиток геометрії 1.1 Історія геометрії 1.2 Постулати Евкліда 1.3 Аксіоматика Гильберта 1.4 Інші системи аксіом геометрії ... Крапки прямій, обумовленої А и В, що лежать між ними, будемо називати внутрішніми крапками, або просто крапками відрізка АВ. Ми ж у своїй моделі будемо називати "прямій" будь-яке лінійне рівняння виду ax + by + c = 0, у якому хоча б один з коефіцієнтів a і b відмінний від нуля, причому коефіцієнти ... |
Раздел: Рефераты по математике Тип: дипломная работа |