Контрольная работа: Розв’язання лінійних задач методами лінійного програмування
Варіант 06
Чернігів 2009
Зміст
Завдання №1
Завдання №2
Завдання №3
Завдання №4
Завдання №5
Список використаних джерел
Завдання №1
Звести до канонічної форми задачу лінійного програмування:
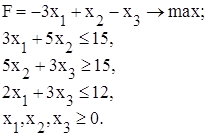
Дана задача лінійного програмування задана в симетричній формі запису: умови, при яких функція F буде максимальною, задані у вигляді нерівностей. Для того, щоб отримати канонічну форму задачі лінійного програмування необхідно нерівності перетворити у рівності, використовуючи теорему, за якою нерівність
![]()
еквівалентна рівнянню
![]() і нерівності
і нерівності ![]()
а нерівність вигляду
![]()
еквівалентна рівнянню
![]() , в якому
, в якому ![]()
Враховуючи наведене вище дану задачу запишемо у наступній канонічній формі:
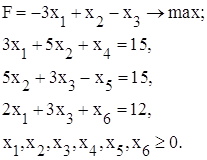
Визначити оптимальний план задачі лінійного програмування графічним методом (знайти максимум і мінімум функції):
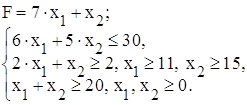
Для задач з двома змінними можна використовувати графічний спосіб розв’язку задач лінійного програмування. Побудуємо область допустимих розв’язків системи лінійних нерівностей. Для цього будуємо відповідні даним нерівностям граничні прямі:
![]()
Потім знаходимо напівплощини, в яких виконуються задані нерівності (рисунок1).
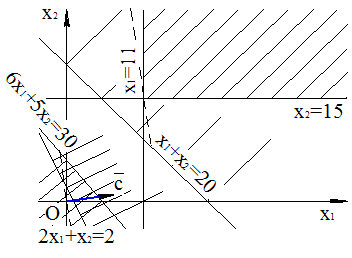
Рисунок1– Графічне визначення максимального і мінімального значення функції
Область
допустимих рішень визначається як загальна частина напівплощин, відповідних
даним нерівностям, які при цьому знаходяться в першій четвертині, тобто
обмежуються прямими ![]() і
і ![]() . З малюнку 1 видно, що
функція не має рішення, оскільки напівплощина, утворена прямими
. З малюнку 1 видно, що
функція не має рішення, оскільки напівплощина, утворена прямими
![]()
не співпадає з площиною, утвореною обмеженнями
![]()
![]() .
.
Побудувати двоїсту задачу. Симплексним методом знайти оптимальний план початкової задачі. Використовуючи першу теорему двоїстості, визначити план другої задачі.
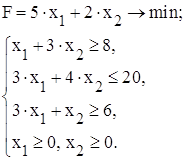
Для перетворення нерівностей в рівності вводимо змінні одиничні матриці х3, х4 і х5. Для розв’язку задачі симплексним методом необхідно мати три одиничних матриці при невід’ємних правих частинах рівнянь. Для отримання одиничної матриці в першій і третій нерівностях вводимо введемо штучні змінну х6 і х7 та отримаємо одиничні матриці А6 і А7. Де
![]() і
і ![]()
В результаті наведених перетворень отримаємо наступну задачу:
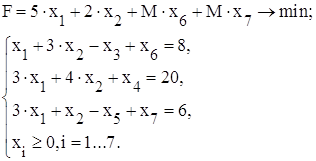
У виразі функції величину М вважаємо достатньо великим додатнім числом, оскільки задача розв’язується на знаходження мінімального значення функції.
Запишемо задачу у векторній формі:
![]()
де
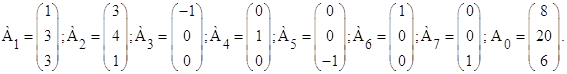
В якості базису
вибираємо одиничні вектори А6, А4, А7. Вільні
невідомі прирівнюємо нулю ![]() . В
результаті отримаємо початковий опорний план розширеної задачі
. В
результаті отримаємо початковий опорний план розширеної задачі
![]() ,
,
якому відповідає розкладення
![]()
Для перевірки
початкового опорного плану складаємо першу симплексну таблицю (таблиця1) і
підраховуємо значення функції ![]() і
оцінок
і
оцінок ![]() Маємо:
Маємо:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
тобто оскільки М
попередньо не фіксовано, то оцінки ![]() є
лінійними функціями величини М, причому функція складається з двох доданків,
одне з яких залежить від М, інше не залежить. Для зручності розрахунків в (F-C) рядок запишемо доданок, незалежний
від М, а в (М) рядок – тільки коефіцієнти при М, які і дозволяють порівняти
оцінки між собою. Для векторів базису оцінки дорівнюють нулю.
є
лінійними функціями величини М, причому функція складається з двох доданків,
одне з яких залежить від М, інше не залежить. Для зручності розрахунків в (F-C) рядок запишемо доданок, незалежний
від М, а в (М) рядок – тільки коефіцієнти при М, які і дозволяють порівняти
оцінки між собою. Для векторів базису оцінки дорівнюють нулю.
Таблиця1– Перша симплексна таблиця
| Базис | С базису |
А0 |
|
|
|
|
|
|
|
|
х1 |
х2 |
х3 |
х4 |
х5 |
х6 |
х7 |
|||
|
х6 |
М | 8 | 1 |
|
-1 | 0 | 0 | 1 | 0 |
|
х4 |
0 | 20 | 3 | 4 | 0 | 1 | 0 | 0 | 0 |
|
х7 |
М | 6 | 3 | 1 | 0 | 0 | -1 | 0 | 1 |
| F-C | – | 0 | -5 | -2 | 0 | 0 | 0 | 0 | 0 |
| М | – | 14 | 4 | 4 | -1 | 0 | -1 | 0 | 0 |
В (М) рядку є додатні
оцінки, тому опорний план Х0 не є оптимальним і його можна покращити,
включивши в базис вектор, якому відповідає ![]() . Оскільки у нас
максимальне значення 4 належить двом векторам, то в базис включаємо вектор,
якому відповідає мінімальне Сj. Розв’язувальним рядком вибирається той, в якому найменше
відношення
. Оскільки у нас
максимальне значення 4 належить двом векторам, то в базис включаємо вектор,
якому відповідає мінімальне Сj. Розв’язувальним рядком вибирається той, в якому найменше
відношення ![]() Серед коефіцієнтів
розкладання векторів А1 і А2 по базису є додатні, тому
хоча б один з векторів існує.. Знайдемо ці значення:
Серед коефіцієнтів
розкладання векторів А1 і А2 по базису є додатні, тому
хоча б один з векторів існує.. Знайдемо ці значення:
![]()
![]() ;
; ![]()
![]()
Таким чином підтвердилося, що розв’язувальним стовпчиком буде другий, і визначилося, що розв’язувальним рядком буде перший. Тобто розв’язувальний елемент – число 3. Тоді вектор А2 включаємо в базис, а вектор А6 виключаємо з нього.
Складаємо другу симплексну таблицю (таблиця2). При цьому елементи першого (розв’язувального) рядка ділимо на 3. Елементи інших рядків визначаємо використовуючи формули повного виключення Йордана-Гауса.
Таблиця2– Друга симплексна таблиця
| Базис | С базису |
А0 |
|
|
|
|
|
|
|
|
х1 |
х2 |
х3 |
х4 |
х5 |
х6 |
х7 |
|||
|
х2 |
2 | 2,67 | 0,33 | 1 | -0,33 | 0 | 0 | 0,33 | 0 |
|
х4 |
0 | 9,33 | 1,67 | 0 | 1,33 | 1 | 0 | -1,33 | 0 |
|
х7 |
М | 3,33 |
|
0 | 0,33 | 0 | -1 | -0,33 | 1 |
| F-C | – | 5,33 | -4,33 | 0 | -0,67 | 0 | 0 | 0,67 | 0 |
| М | – | 3,33 | 2,67 | 0 | 0,33 | 0 | -1 | -1,33 | 0 |
В (М) рядку є
додатні оцінки, тому план, зображений в таблиці2 не є оптимальним і його можна
покращити, включивши в базис вектор, якому відповідає ![]() . Тобто за розв’язувальний
стовпчик вибираємо перший. Мінімальне відношення
. Тобто за розв’язувальний
стовпчик вибираємо перший. Мінімальне відношення
![]()
тому розв’язувальним рядком є третій. Таким чином розв’язувальний елемент – число 2,67. Тоді вектор А1 включаємо в базис, а вектор А7 виключаємо з нього.
Складаємо другу симплексну таблицю (таблиця3). При цьому елементи третього (розв’язувального) рядка ділимо на 2,67. Елементи інших рядків визначаємо використовуючи формули повного виключення Йордана-Гауса.
Таблиця3– Третя симплексна таблиця
| Базис | С базису |
А0 |
|
|
|
|
|
|
|
|
х1 |
х2 |
х3 |
х4 |
х5 |
х6 |
х7 |
|||
|
х2 |
2 | 2,25 | 0 | 1 | -0,375 | 0 | 0,125 | 0,375 | -0,125 |
|
х4 |
0 | 7,25 | 0 | 0 | 1,125 | 1 | 0,625 | -1,125 | -0,625 |
|
х1 |
5 | 1,25 | 1 | 0 | 0,125 | 0 | -0,375 | -0,125 | 0,375 |
| F-C | – | 10,75 | 0 | 0 | -0,125 | 0 | -1,625 | 0,125 | 1,625 |
| М | – | 0 | 0 | 0 | 0 | 0 | 0 | -1 | -1 |
В результаті проведеної ітерації з базису виключено штучні елементи, тому в рядку (М) всі оцінки, крім оцінки штучного вектору, перетворилися на нуль. Оскільки в рядках (F-C) і (М) не має додатних значень, то знайдене рішення
(![]() )
)
є оптимальним. Функція при цьому
![]()
Перевірка
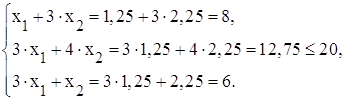
Кожній задачі
лінійного програмування можна поставити у відповідність двоїсту задачу. Для
цього першим кроком необхідно впорядкувати запис вихідної задачі. Оскільки у
нас функція мінімізується, то всі умови-нерівності повинні бути вигляду ![]() . Виконання цієї умови
досягаємо множенням відповідних умов на (1-). В результаті система обмежень
матиме наступний вигляд:
. Виконання цієї умови
досягаємо множенням відповідних умов на (1-). В результаті система обмежень
матиме наступний вигляд:
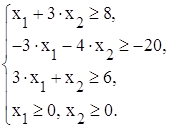
Оскільки вихідна
задача є задачею мінімізації, то двоїста буде задачею максимізації. Двоїста
задача буде мати три змінні ![]() ,
оскільки вихідна задача має три обмеження. При цьому вектор, отриманий із
коефіцієнтів при невідомих цільової функції вихідної задачі
,
оскільки вихідна задача має три обмеження. При цьому вектор, отриманий із
коефіцієнтів при невідомих цільової функції вихідної задачі ![]() , співпадає з вектором
констант у правих частинах обмежень двоїстої задачі. Аналогічно пов’язані між
собою вектори, утворені з коефіцієнтів при невідомих цільової функції двоїстої
задачі
, співпадає з вектором
констант у правих частинах обмежень двоїстої задачі. Аналогічно пов’язані між
собою вектори, утворені з коефіцієнтів при невідомих цільової функції двоїстої
задачі ![]() , і константи в правих
частинах обмежень вихідної задачі. Кожній змінній
, і константи в правих
частинах обмежень вихідної задачі. Кожній змінній ![]() двоїстої
задачі відповідає і-те обмеження вихідної задачі, і, навпаки, кожній змінній
двоїстої
задачі відповідає і-те обмеження вихідної задачі, і, навпаки, кожній змінній ![]() прямої задачі відповідає j-те обмеження двоїстої задачі.
Матриця з коефіцієнтів при невідомих двоїстої задачі
прямої задачі відповідає j-те обмеження двоїстої задачі.
Матриця з коефіцієнтів при невідомих двоїстої задачі ![]() утворюється
транспортуванням матриці А, складеної з коефіцієнтів при невідомих вихідної
задачі. Якщо на j-ту
змінну вихідної задачі накладена умова невід’ємності, то j-те обмеження двоїстої задачі буде
нерівністю, в іншому випадку j-те обмеження буде рівністю; аналогічно пов’язані між собою обмеження
вихідної задачі і змінні двоїстої.
утворюється
транспортуванням матриці А, складеної з коефіцієнтів при невідомих вихідної
задачі. Якщо на j-ту
змінну вихідної задачі накладена умова невід’ємності, то j-те обмеження двоїстої задачі буде
нерівністю, в іншому випадку j-те обмеження буде рівністю; аналогічно пов’язані між собою обмеження
вихідної задачі і змінні двоїстої.
Складаємо матрицю при невідомих вихідної задачі:
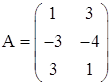 ,
,
тоді матриця при невідомих двоїстої задачі матиме наступний вигляд:
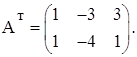
На ![]() накладено умову
невід’ємності, тому обмеження двоїстої задачі матимуть вигляд нерівності, а не
рівності. Оскільки в початковій задачі всі обмеження мають вигляд нерівності,
то накладаємо умови
накладено умову
невід’ємності, тому обмеження двоїстої задачі матимуть вигляд нерівності, а не
рівності. Оскільки в початковій задачі всі обмеження мають вигляд нерівності,
то накладаємо умови ![]()
Враховуючи все наведене, двоїста задача матиме наступний вигляд:
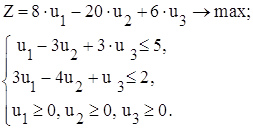
Якщо розглянути
першу симплексну таблицю з одиничним додатковим базисом, то можна помітити, що
в стовбцях записана вихідна задача, а в рядках – двоїста. Причому оцінками
плану вихідної задачі є ![]() , а
оцінками плану двоїстої задачі –
, а
оцінками плану двоїстої задачі – ![]() З
таблиці3, отриманої в результаті рішення вихідної задачі знаходимо:
З
таблиці3, отриманої в результаті рішення вихідної задачі знаходимо:
![]()
Визначити оптимальний план транспортної задачі:
а) побудувати початковий опорний план методом "північно-західного" напрямку;
б) побудувати оптимальний план методом потенціалів:
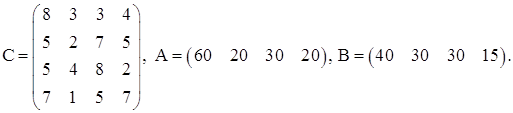
Нехай в матриці А міститься інформація про кількість продукту в кожному місці виробництва, який необхідно доставити споживачам в кількості записаній в матриці В. Транспортні витрати, пов’язані з перевезенням одиниці продукту із одного місця виробництва одному споживачеві, записані в матриці С. Задані матриці і сказане вище для спрощення сприйняття узагальнимо в таблиці4.
Таблиця4–Поставка продукту із різних місць виробництва різним споживачам і пов’язані з цим витрати
| Виробник | Споживач | Запаси продукту | |||
|
|
|
|
|
||
|
|
8 | 3 | 3 | 4 | 60 |
|
|
5 | 2 | 7 | 5 | 20 |
|
|
5 | 4 | 8 | 2 | 30 |
|
|
7 | 1 | 5 | 7 | 20 |
| Потреба в продукті | 40 | 30 | 30 | 15 |
130 115 |
З таблиці4 видно,
що запаси продукту у виробника на складах на 15 одиниць більші ніж необхідно
споживачу, тобто маємо транспортну задачу з відкритою моделлю. Для розв’язку
такої задачі введемо фіктивного споживача, якому необхідно отримати ![]() одиниць продукту. Всі
тарифи на доставку продукту цьому споживачеві будемо вважати рівними нулю, і
весь продукт потрібний цьому споживачеві залишаємо у місці виробництва. Для
побудови початкового плану перевезень (таблиця5) використаємо метод "північно-західного"
напрямку: заповнювати таблицю починаємо з лівого верхнього кута, рухаючись вниз
по стовбцю або вправо по рядку (тарифи перевезень напишемо в правому верхньому
куту кожної клітини, кількість продукту – в нижньому лівому). В першу клітину
заносимо менше з чисел (min(40;60): 40. Тобто потреба в продукті першого споживача повністю задовільнено
і інші клітини першого стовпця заповнювати не будемо. Рухаємося далі по першому
рядку в другий стовпчик. В цю клітину записуємо менше з 30 і (60-40), тобто пишемо 20. Таким чином перший рядок
заповнювати далі не будемо, оскільки запаси першого місця виробництва остаточно
вичерпано: з нього ми повністю задовольняємо потребу у продукті першого
споживача і частково (20 одиниць, а не 30) другого. Рухаємося по другому
стовпчику на другий рядок. Сюди записуємо менше з (30-20) або 20: маємо 10,
тобто другому споживачеві ми веземо 20одиниць продукту з першого місця
виробництва і 10– з другого. Аналогічно заповнюємо інші клітини.
одиниць продукту. Всі
тарифи на доставку продукту цьому споживачеві будемо вважати рівними нулю, і
весь продукт потрібний цьому споживачеві залишаємо у місці виробництва. Для
побудови початкового плану перевезень (таблиця5) використаємо метод "північно-західного"
напрямку: заповнювати таблицю починаємо з лівого верхнього кута, рухаючись вниз
по стовбцю або вправо по рядку (тарифи перевезень напишемо в правому верхньому
куту кожної клітини, кількість продукту – в нижньому лівому). В першу клітину
заносимо менше з чисел (min(40;60): 40. Тобто потреба в продукті першого споживача повністю задовільнено
і інші клітини першого стовпця заповнювати не будемо. Рухаємося далі по першому
рядку в другий стовпчик. В цю клітину записуємо менше з 30 і (60-40), тобто пишемо 20. Таким чином перший рядок
заповнювати далі не будемо, оскільки запаси першого місця виробництва остаточно
вичерпано: з нього ми повністю задовольняємо потребу у продукті першого
споживача і частково (20 одиниць, а не 30) другого. Рухаємося по другому
стовпчику на другий рядок. Сюди записуємо менше з (30-20) або 20: маємо 10,
тобто другому споживачеві ми веземо 20одиниць продукту з першого місця
виробництва і 10– з другого. Аналогічно заповнюємо інші клітини.
Таблиця5– Розподіл продукту по споживачам
| Виробник | Споживач | Запаси продукту | ||||
|
|
|
|
|
|
||
|
|
8 | 3 | 3 | 4 | 0 | 60 |
| 40 | 20 | |||||
|
|
5 | 2 | 7 | 5 | 0 | 20 |
| 10 | 10 | |||||
|
|
5 | 4 | 8 | 2 | 0 | 30 |
| 20 | 10 | |||||
|
|
7 | 1 | 5 | 7 | 0 | 20 |
| 5 | 15 | |||||
| Потреба в продукті | 40 | 30 | 30 | 15 | 15 | 130 |
Таким чином, в таблиці5 отримали початковий опорний план, транспортні витрати за яким складають:
![]()
Недоліком використаного методу знаходження опорного плану є ігнорування величини тарифів на перевезення продукту.
Для визначення оптимального
плану перевезень використаємо метод потенціалів. Для цього кожному виробнику Аі
(кожному рядку) ставимо у відповідність деяке число ![]() а
кожному споживачу Ві (кожному стовпчику)– деяке число
а
кожному споживачу Ві (кожному стовпчику)– деяке число ![]() На основі таблиці5
складемо таблицю6, в якій додамо один стовпчик і один рядок для написання
величини параметрів
На основі таблиці5
складемо таблицю6, в якій додамо один стовпчик і один рядок для написання
величини параметрів ![]() і
і ![]() . Їх знаходимо
використовуючи першу умову оптимальності транспортної задачі:
. Їх знаходимо
використовуючи першу умову оптимальності транспортної задачі: ![]() (для кожної зайнятої
клітини сума потенціалів повинна дорівнювати вартості одиниці перевезення, що
записана в цій клітині).
(для кожної зайнятої
клітини сума потенціалів повинна дорівнювати вартості одиниці перевезення, що
записана в цій клітині).
Таблиця6– Перевірка оптимальності опорного плану
| Виробник | Споживач | Запаси продукту |
|
||||
|
|
|
|
|
|
|||
|
|
8 | 3 | 3 | 4 | 0 | 60 | 0 |
| 40 | 20 | ||||||
|
|
5 | 2 | 7 | 5 | 0 | 20 | -1 |
| 10 | 10 | ||||||
|
|
5 | 4 |
|
2 | 0 | 30 | 0 |
| 20 | 10 | ||||||
|
|
7 | 1 | 5 | 7 | 0 | 20 | 5 |
| 5 | 15 | ||||||
| Потреба в продукті | 40 | 30 | 30 | 15 | 15 | 130 | × |
|
|
8 | 3 | 8 | 2 | -5 | × | × |
Систему
потенціалів можна побудувати лише для невирожденого опорного плану. Такий план
містить m+n-1 лінійно незалежних рівнянь виду ![]() з m+n невідомими (де m– кількість постачальників, n– кількість споживачів). Рівнянь на
одне менше, ніж невідомих, тому система є невизначеною і для її розв’язку одному
невідомому (нехай ним буде u1) придамо нульове значення.
з m+n невідомими (де m– кількість постачальників, n– кількість споживачів). Рівнянь на
одне менше, ніж невідомих, тому система є невизначеною і для її розв’язку одному
невідомому (нехай ним буде u1) придамо нульове значення.
Для того, щоб
план був оптимальним, повинна виконуватись умова: для кожної незайнятої клітини
сума потенціалів повинна бути менша або дорівнювати вартості одиниці
перевезення, що стоїть в цій клітині: ![]() тобто
тобто ![]() Робимо перевірку для всіх
вільних клітин:
Робимо перевірку для всіх
вільних клітин:
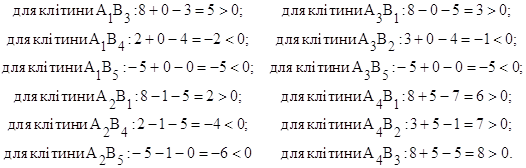
З розрахунків бачимо, що умова оптимальності не виконується для клітин, А1В3, А2В1, А3В1, А4В1, А4В2, і А4В3. Клітину, в якій додатне число отримали максимальним (А2В3, оскільки max(5;2;3;6;7;8)=8) зробимо зайнятою, для цього побудуємо цикл і отримуємо таблицю7.
Таблиця7– Другий крок пошуку оптимального рішення
| Виробник | Споживач | Запаси продукту |
|
||||
|
|
|
|
|
|
|||
|
|
8 |
|
3 | 4 | 0 | 60 | 0 |
| 40 | 20 | ||||||
|
|
5 | 2 | 7 | 5 | 0 | 20 | -1 |
| 10 | 10 | ||||||
|
|
5 | 4 | 8 | 2 | 0 | 30 | 0 |
| 15 | 15 | ||||||
|
|
7 | 1 | 5 | 7 | 0 | 20 | -3 |
| 5 | 15 | ||||||
| Потреба в продукті | 40 | 30 | 30 | 15 | 15 | 130 | × |
|
|
8 | 3 | 8 | 2 | 3 | × | × |
Транспортні витрати при такому плані перевезення складають:
![]()
Перевірка всіх вільних клітин:
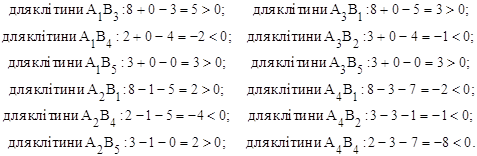
Отримали від’ємні значення у всіх клітинах окрім А1В3 (5), А1В5 (3), А2В1 (2), А2В5 (2), А3В1 (3) і А3В5 (3). Максимальне значення max(5;3;2;2;3;3)=5 в клітині А1В3, тому заповнюємо і цикл будуємо для неї (цикл показано в таблиці7, результат дій в таблиці8).
Таблиця8– Третій крок пошуку оптимального рішення
| Виробник | Споживач | Запаси продукту |
|
||||
|
|
|
|
|
|
|||
|
|
8 | 3 | 3 | 4 | 0 | 60 | - |
| 40 | 10 | 10 | |||||
|
|
5 | 2 | 7 | 5 | 0 | 20 | -1 |
| 20 | |||||||
|
|
5 | 4 | 8 | 2 | 0 | 30 | 5 |
| 15 | 15 | ||||||
|
|
7 | 1 | 5 | 7 | 0 | 20 | 2 |
| 5 | 15 | ||||||
| Потреба в продукті | 40 | 30 | 30 | 15 | 15 | 130 | × |
|
|
8 | 3 | 3 | -3 | -2 | × | × |
Транспортні витрати:
![]()
тобто при такому плані перевезення товару транспортні витрати знизилися на 50грн. в порівнянні з попереднім планом перевезення. Але, щоб визначити є отриманий план оптимальним чи ні, виконаємо перевірку.
Перевірку всіх вільних клітин зобразимо в таблиці9, в якій для всіх вільних клітин запишемо різницю між сумою потенціалів і транспортними витратами в клітині.
Таблиця9– Перевірка плану отриманого в результаті третього кроку пошуку оптимального рішення задачі
|
|
|
|
|
|
|
|
|
- | - | - | -7 | -2 |
|
|
2 | - | -5 | -9 | -3 |
|
|
8 | 4 | - | - | 3 |
|
|
3 | 4 | - | -8 | - |
З таблиці9 видно, що додатне значення отримали для клітин А2В1 (2), А3В1 (8), А3В2 (4), А3В5 (3), А4В1 (3) і А4В2 (4). Максимальне значення max(2;8;4;3;3;4)=8 в клітині А3В1, тому заповнюємо і цикл будуємо для неї (цикл показано в таблиці8, результат дій в таблиці10).
Таблиця1– Четвертий крок пошуку оптимального рішення задачі
| Виробник | Споживач | Запаси продукту |
|
||||
|
|
|
|
|
|
|||
|
|
8 |
|
3 | 4 | 0 | 60 | 0 |
| 25 | 10 | 25 | |||||
|
|
5 | 2 | 7 | 5 | 0 | 20 | -1 |
| 20 | |||||||
|
|
5 | 4 | 8 | 2 | 0 | 30 | -3 |
| 15 | 15 | ||||||
|
|
7 | 1 | 5 | 7 | 0 | 20 | 2 |
| 5 | 15 | ||||||
| Потреба в продукті | 40 | 30 | 30 | 15 | 15 | 130 | × |
|
|
8 | 3 | 3 | 5 | -2 | × | × |
Транспортні витрати:
![]()
що на 120грн. економніше попереднього варіанту розвезення продукції від постачальників до споживачів.
Перевірка всіх вільних клітин наведена в таблиці11.
Таблиця11– Різниця між сумою потенціалів і транспортними витратами для вільних клітин
|
|
|
|
|
|
|
|
|
- | - | - | 1 | -2 |
|
|
2 | - | -5 | -1 | -3 |
|
|
- | -4 | -8 | - | -5 |
|
|
3 | 4 | - | 0 | - |
План, зображений в таблиці10 не є оптимальним, оскільки отримали додатні значення в клітинах А1В4 (1), А2В1 (2), А4В1 (3), А4В2 (4). Заповнюємо клітину А4В2 і будуємо опорний план (таблиця12).
Таблиця12– П’ятий крок пошуку оптимального рішення задачі
| Виробник | Споживач | Запаси продукту |
|
||||
|
|
|
|
|
|
|||
|
|
8 |
|
3 | 4 | 0 | 60 | 0 |
| 25 | 5 | 30 | |||||
|
|
5 | 2 | 7 | 5 | 0 | 20 | -1 |
| 20 | |||||||
|
|
5 | 4 | 8 | 2 | 0 | 30 | -3 |
| 15 | 15 | ||||||
|
|
7 | 1 | 5 | 7 | 0 | 20 | -2 |
| 5 | 15 | ||||||
| Потреба в продукті | 40 | 30 | 30 | 15 | 15 | 130 | × |
|
|
8 | 3 | 3 | 5 | 2 | × | × |
Транспортні витрати за отриманим планом перевезень складають:
![]()
що на 20грн. економніше попереднього варіанту розвезення продукції від постачальників до споживачів.
Перевірка всіх вільних клітин здійснена в таблиці 13.
Таблиця13– Різниця між сумою потенціалів і транспортними витратами для вільних клітин
|
|
|
|
|
|
|
|
|
- | - | - | 1 | 2 |
|
|
2 | - | -5 | -1 | 1 |
|
|
- | -4 | -8 | - | -1 |
|
|
-1 | - | -4 | -4 | - |
Оскільки в результаті розрахунків отримали додатні значення, то знову будуємо цикл і заповнюємо необхідну клітину. В даному випадку це буде або клітина А2В1 або клітина А1В5. Вибираємо останню, оскільки транспортні витрати на перевезення в ній менші. На від’ємних кутах циклу об’єм перевезень становить 10 і 0. Оскільки min(10;0)=0, то всі клітини залишаються незмінними і лише клітина з нульовим перевезенням переходить з А4В5 на А1В5.
Новий план зображено в таблиці14.
Таблиця14– Шостий крок пошуку оптимального рішення задачі
| Виробник | Споживач | Запаси продукту |
|
||||
|
|
|
|
|
|
|||
|
|
|
3 | 3 | 4 | 0 | 60 | 0 |
| 25 | 30 | 5 | |||||
|
|
5 | 2 | 7 | 5 | 0 | 20 | -1 |
| 20 | |||||||
|
|
5 | 4 | 8 | 2 | 0 | 30 | -3 |
| 15 | 15 | ||||||
|
|
7 | 1 | 5 | 7 | 0 | 20 | 0 |
| 10 | 10 | ||||||
| Потреба в продукті | 40 | 30 | 30 | 15 | 15 | 130 | × |
|
|
8 | 1 | 3 | 5 | 0 | × | × |
Транспортні витрати за отриманим планом перевезень складають:
![]()
Розрахунки для перевірка всіх вільних клітин здійснені в таблиці 15:
Таблиця15– Різниця між сумою потенціалів і транспортними витратами для вільних клітин
|
|
|
|
|
|
|
|
|
- | -2 | - | 1 | - |
|
|
4 | - | -3 | 1 | 1 |
|
|
- | -6 | -8 | - | -3 |
|
|
1 | - | -2 | -2 | - |
З таблиці15 видно, що максимальне додатне значення отримали для клітини А2В1, тому заповнюємо її будуючи для неї цикл, який показано в таблиці14. Результат дій в таблиці16.
Таблиця16– Сьомий крок пошуку оптимального рішення задачі
| Виробник | Споживач | Запаси продукту |
|
||||
|
|
|
|
|
|
|||
|
|
|
3 | 3 | 4 | 0 | 60 | 0 |
| 15 | 30 | 15 | |||||
|
|
5 | 2 | 7 | 5 | 0 | 20 | -3 |
| 105 | 0 | 20 | -3 | ||||
| 10 | 10 | ||||||
|
|
5 | 4 | 8 | 2 | 0 | 30 | -3 |
| 15 | 15 | ||||||
|
|
7 | 1 | 5 | 7 | 0 | 20 | -4 |
| 20 | |||||||
| Потреба в продукті | 40 | 30 | 30 | 15 | 15 | 130 | × |
|
|
8 | 5 | 3 | 5 | 0 | × | × |
Транспортні витрати:
![]()
що на 40грн. економніше попереднього варіанту розвезення продукції від постачальників до споживачів.
Перевірка всіх вільних клітин наведена в таблиці17.
Таблиця17– Різниця між сумою потенціалів і транспортними витратами для вільних клітин
|
|
|
|
|
|
|
|
|
- | 2 | - | 1 | - |
|
|
- | - | -7 | -3 | -3 |
|
|
- | -2 | -8 | - | -3 |
|
|
-3 | - | -6 | -6 | -4 |
План, зображений в таблиці8 не є оптимальним, оскільки отримали додатні значення в клітинах А1В2 (2) і А1В4 (1). Заповнюємо клітину А1В2 і будуємо опорний план (таблиця18).
Таблиця18– Восьмий крок пошуку оптимального рішення задачі
| Виробник | Споживач | Запаси продукту |
|
||||
|
|
|
|
|
|
|||
|
|
|
3 | 3 | 4 | 0 | 60 | 0 |
| 5 | 10 | 30 | 15 | ||||
|
|
5 | 2 | 7 | 5 | 0 | 20 | -3 |
| 20 | |||||||
|
|
5 | 4 | 8 | 2 | 0 | 30 | -3 |
| 15 | 15 | ||||||
|
|
7 | 1 | 5 | 7 | 0 | 20 | -2 |
| 20 | |||||||
| Потреба в продукті | 40 | 30 | 30 | 15 | 15 | 130 | × |
|
|
8 | 3 | 3 | 5 | 0 | × | × |
Транспортні витрати за отриманим планом перевезень складають:
![]()
що на 20грн. економніше попереднього варіанту розвезення продукції від постачальників до споживачів. Перевірка всіх вільних клітин здійснена в таблиці 19.
Таблиця19– Різниця між сумою потенціалів і транспортними витратами для вільних клітин
|
|
|
|
|
|
|
|
|
- | - | - | 1 | - |
|
|
- | -2 | -7 | -3 | -3 |
|
|
- | -4 | -8 | - | -3 |
|
|
-1 | - | -4 | -4 | -2 |
Оскільки в результаті розрахунків отримали додатне значення в єдиній клітині А1В4, то будуємо цикл і заповнюємо її. Новий план зображено в таблиці20.
Таблиця20– Дев’ятий крок пошуку оптимального рішення задачі
| Виробник | Споживач | Запаси продукту |
|
||||
|
|
|
|
|
|
|||
|
|
8 | 3 | 3 | 4 | 0 | 60 | 0 |
| 10 | 30 | 5 | 15 | ||||
|
|
5 | 2 | 7 | 5 | 0 | 20 | -2 |
| 20 | |||||||
|
|
5 | 4 | 8 | 2 | 0 | 30 | -2 |
| 20 | 10 | ||||||
|
|
7 | 1 | 5 | 7 | 0 | 20 | -2 |
| 20 | |||||||
| Потреба в продукті | 40 | 30 | 30 | 15 | 15 | 130 | × |
|
|
7 | 3 | 3 | 4 | 0 | × | × |
Розрахунки для перевірка всіх вільних клітин здійснені в таблиці 21:
Таблиця21– Різниця між сумою потенціалів і транспортними витратами для вільних клітин
|
|
|
|
|
|
|
|
|
-1 | - | - | - | - |
|
|
- | -1 | -6 | -3 | -2 |
|
|
- | -3 | -7 | - | -2 |
|
|
-2 | - | -4 | -5 | -2 |
Рішення, зображене в таблиці20 є оптимальним, оскільки для кожної незайнятої клітини сума потенціалів менша вартості перевезень, що знаходиться у відповідній клітинці. Транспортні витрати по оптимальному плану перевезень становлять:
![]()
Знайдений оптимальний план покращив результат діяльності у порівнянні з початковим (зменшив транспортні витрати) на 685-380=305гривень.
Список використаних джерел
1. Кузнецов Ю.Н. Математическое программирование. Учебное пособие для вузов– М.: Высшая школа, 1976.– 352с.
2. Кузнецов А.В., Холод Н.И., Костевич Л.С. Руководство к решению задач по математическому программированию.– Мн.: Высш. школа, 1978.– 256с.
 8
8 3
3
 3
3  3
3  8
8 8
8 8
8